基于目标规划模型的新建学校选址问题

耿淑莉 赵红

摘  要：基础教育设施中新建学校选址是很重要的问题，本文基于某市某区2017年公立小学学区划分情况，由出行成本确定备选点，利用目标规划方法，在Lingo和MATLAB软件支持下进行新建学校选址。以降低总体出行成本和提高总体服务效用为目标，依据学校、居民单元及道路交通数据，构建学区划分优化的多目标线性规划模型。采用线性加权方法将多目标问题转化为单目标问题进行求解，在此基础上建立新建学校选址的非线性目标规划模型，进一步缩小备选点的范围。最后利用学区划分优化模型逐个测试余下备选点，得到新建学校的最优选址。

关键词：目标规划  学区划分优化  新建学校选址  Huff模型

中图分类号：P208                             文献标识码：A                文章编号：1674-098X（2020）08（a）-0239-04

Abstract： The location of new schools in basic education facilities is a very important issue. Based on the division of public primary school districts in a certain district of a city in 2017， the candidate points are determined by the travel cost， and the goal programming method is used to solve this problem with the support of Lingo and MATLAB software. With the goal of reducing overall travel costs and improving overall service utility， based on school， residential unit and road traffic data， a multi-objective linear programming model for the optimization of school district division is constructed. The linear weighting method is used to convert the multi-objective problem into a single-objective problem for solution. And on this basis， a nonlinear goal programming model for the location of new schools is established to further narrow the range of candidate points. Finally， the school district division optimization model is used to test the remaining candidate points one by one to obtain the most optimal location for the new school.

Key Words： Goal programming; Optimization of school district division; Location selection of new school; Huffmodel

基礎教育是国家发展的基础，其均衡发展逐渐成为我国关注的重点。但在我国义务教育实施过程中就近入学难与择校现象依旧比较突出，主要原因就在于空间分布不均、学校规模不合理与学区划分不妥当[1]。本文考虑建立新学校优化教育资源，为政府部门提供决策意见。为此，本文基于运筹学知识，建立了系列目标规划模型研究新建学校选址问题。

1  研究区域概况

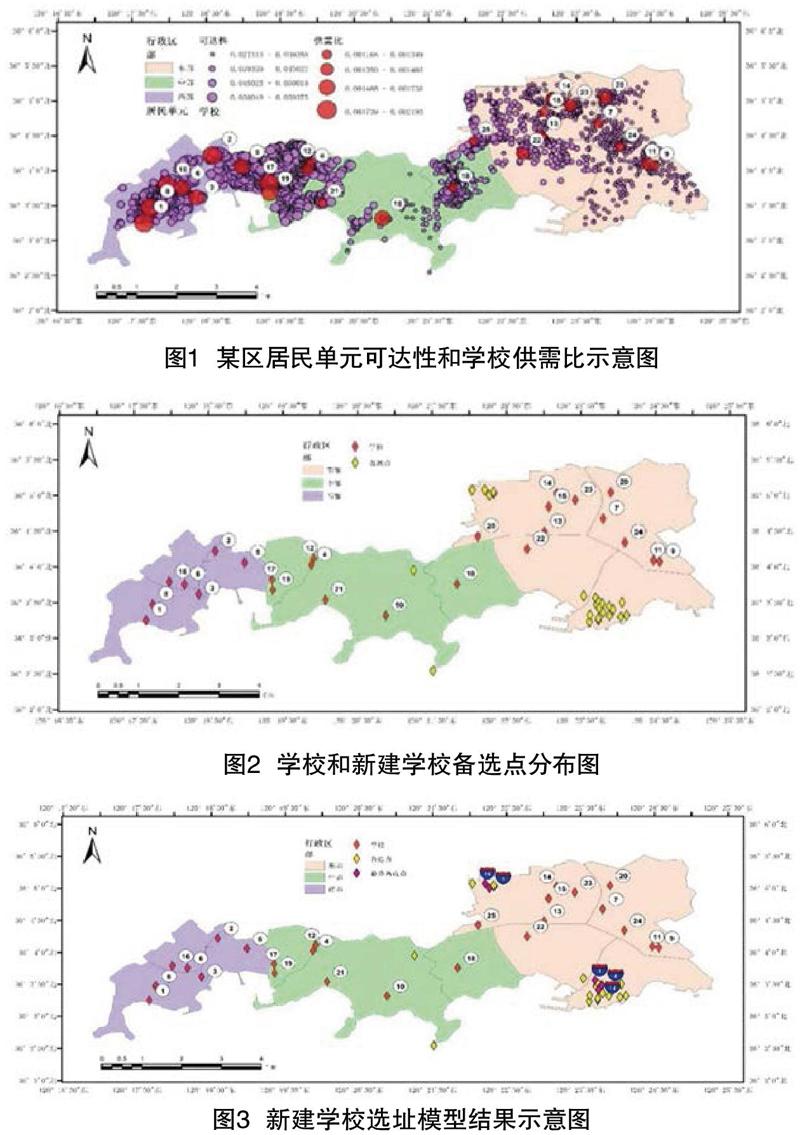
某区是某市行政区之一，截至2017年末，全区常住人口达58.53万人，公立小学25所。根据该区某路某号划分居民单元，共有1736个居民单元。本文采用具有距离衰减系数的结合重力模型的两步移动搜索法[2]，计算了居民单元可达性（表示学生获取学校服务的难易程度）和学校供需比（表示学校人均服务能力），可达性越高说明获取学校服务越容易，供需比越大说明学校服务能力越强。由图1（ 紫色圆点代表居民单元，红色圆点代表学校）可知，该区西部教育资源明显优于中部和东部，说明当地教育资源配置不合理。

2  数据处理

学校数据指学校学位数，本文将学校综合评分作为其服务质量，居民单元数据为单元内居住的在校学生总数，道路交通数据是二者间最短步行时间（速度1.1～1.2m/s）。出于建立模型的实际需要和可操作性，本文利用地图无忧软件绘制了不同时间范围内居民单元的步行区域，最后选择将20min内不能到达任何学校的24个居民单元作为新建学校的备选点。由图2可知，备选点均位于中部和东部，说明该选择是合理的。

3  目标规划模型

3.1 学区划分优化模型

已知当前学区划分存在不合理现象，因此本文在选址前先进行学区划分优化。采用多目标规划方法，本文以就近入学为原则，在学校数量、位置和学位数确定的前提下将全部学生分配到临近学校，使其达到降低总体出行成本和提高总体服务效用j的目标，建立0-1整型线性规划模型：

模型中，居民单元指标集I={1，2，…，m}（m=1736），居民单元i学生数为ai;学校指标集J={1，2，…，n}（n=25），学校j学位数为bj，服务质量为sj;tij为居民单元i到学校j的出行成本（最短步行时间），t0为其限制（60min），pij为学校j对居民单元i的服务效用。根据Huff模型[3]，pij主要取决于sj和tij。学校的服务质量越高，出行成本越低，对居民单元中学生的服务效用也就越大[4]。其中I，J，ai ，bj，sj，tij，t0均为已知量;xij为决策变量，取值为0或1，xij=1表示将居民单元i划分到学校j。

优化目标（1）全部学生到学校的总体出行成本最小，（2）学校对全部学生的总体服务效用最大;约束条件（3）居民单元i中每个学生到学校j的出行成本不能超过限制，（4）划分到学校j的学生不超过其学位数，（5）居民单元i中全部学生划分给某一学校。

本文采用线性加权方法求解该模型[5]，为保证目标函数数量级的一致性，本文由总体出行成本最小模型：优化目标（1），约束条件（3）、（4）、（5）、（6）和总体服务效用最大模型：优化目标（2），约束条件（3）、（4）、（5）、（6），分别得到总体最小出行成本T0和总体最大服务效用P0。将多目标函数归一化处理得单目标函数：

其中α∈[0，1]，以0.1为步长取值，利用Lingo软件可得全局最优解。当α=0时为总体出行成本最小模型，当α=1时为总体服务效用最大模型。

3.2 新建学校选址模型

由于建立新学校目的同样是降低总体出行成本和提高总体服务效用，本文在学区划分优化模型的基础上建立了单目标非线性规划模型，以实现对新建学校备选点的筛选。首先将学校服务质量划分为四个等级：v∈{1，2，3，4}，第v等级的学校服务质量为sv;新建学校备选点指标集K={1，2，…，μ}（μ=24），tik为居民单元i到备选点k的出行成本，pikv为备选点k建立第v等级学校对居民单元i中学生的服务效用[6]。则总体出行成本为;总体服务效用为

其中xik和ykv为决策变量，取值为0或1，xik=1表示将居民单元i划分到备选点k，ykv=1表示备选点k将建立第v等级的学校。约束条件（9）任一居民单元中学生到任意学校的出行成本不能超过其限制;（10）每个居民单元中学生只能划分到某一学校（整体划分）;（11）新建学校的数量为一个;（12）新建学校只能为某一等级;（13）只有在将新建学校的备选点才能划分到居民单元中的学生（整体划分）。

同样将α依次取值，利用Lingo软件可得局部最优解。为得到最优学区划分结果，本文只参考ykv的值，且不考虑等级。通过α的11个取值，最后得到5个备选点k∈{1，4，9，14，16}，分布如图3所示。其中红色菱块代表现有公立小学，黄色菱块代表初始备选点，紫色菱块代表筛选出的5个备选点，其蓝色标号为初始备选点序号。

3.3 确定新建学校选址

为保证新建学校可以达到最优学区划分，本文决定利用学区划分优化模型依次测试上述备选点。此时将学校指标集扩充为J={1，2，…，26}，假设新建学校的学位数，服务质量s26=maxj{sj}，居民单元i到新建学校的出行成本di26=dik。

利用Lingo求解上述系列模型可得全局最优解，再利用MATLAB计算每个模型的总体出行成本T，平均出行成本，总体服务效用P，平均服务效用以及与已知学区划分情况的重叠率lap，重叠率越高说明政府需要调整的地方越少，即可操作性越强。为综合三者对模型的影响，本文定义了模型评价指标F。T越小，P越大，lap越高，其F值越大，也说明该模型的实用性越强。

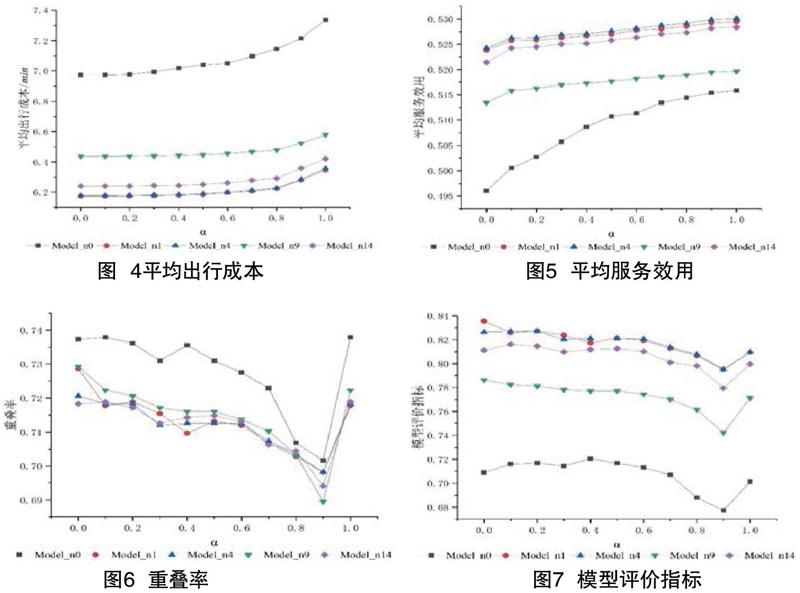
经计算，当前学区划分下=14min，=0.4564， lap=1，F=0.4406。由于k=16时结果比已知情况更糟，没有再考虑的必要性，因此本文仅对比分析其余4个备选点。结果如图4至图7所示，其中Model_n0为没有新建学校的学区划分优化模型，Model_n1、Model_n4、Model_n9、Model_n14分别为在备选点1、4、9、14处新建学校的学区划分优化模型。

从出行成本看（如图4），上述模型均降低一半左右的，考虑新建学校的学区划分优化模型的结果更优，其中Model_n1和Model_n4的下降幅度最大且基本一致，Model_n14略次之，Model_n9下降幅度最小;从服务效用看（如图5），上述模型均提高了，考虑新建学校的学区划分优化模型结果更优也更加稳定，其中Model_n1和Model_n4的上升幅度最大且基本一致，Model_n14略次之，Model_n9上升幅度最小;同时从图4至图5可知，随着α值的增大，各模型的和也随之增大，这与目标函数设置情况一致。从重叠率看（如图6），Model_n0要明显优于其他模型，与实际情况吻合。综合来看（如图7），考虑了新建学校的模型更能满足三个方面的均衡需求，这表明了建立新学校的必要性。其中Model_n1和Model_n4结果最优且基本一致，Model_n14略次之，Model_n9最差。又由图3可知，备选点1和备选点4的位置相近，因此本文将其中点作为新建学校的选址。

4  结语

本文根据某市某区2017年数据，首先从可达性与供需比分析了当地教育资源分配的不合理性，经出行成本确定出备选点后，建立了学区划分优化的多目标线性规划模型和新建学校选址的非线性规划模型，逐步缩小备选点的范围。最后从出行成本、服务效用和重叠率三个角度出发，利用学区划分优化模型依次测试余下的备选点。通过对比F的值可以发现，备选点1和4的结果最优，又考虑到地理因素，本文将其二者中点作为新建学校的最终选址。通过与已知学区划分情况及其优化结果对比可知，本文关于新建学校的选址方法是可行的，能为执政者建立新学校提供辅助帮助。

参考文献

[1] 贺琦.西安市碑林区小学学区划分研究[D].西安：西安建筑科技大学，2018.

[2] 李淑瑶，忻静.基于上海市地理国情成果的学生就学可达性测度与学区优化分析[J].城市勘测，2019（2）：28-34.

[3] 赵冬.HUFF模型的改进及其在城市公园绿地服务能力分析中的应用[D].沈阳：沈阳农业大学，2017.

[4] 刘芳.新零售生鲜超市选址问题研究[J].商讯，2019（4）：27-28.

[5] 周春辉，陈铭章，何义才，等.复杂水网中船舶航行路径多目标规划模型[J].中国航海，2017，40（2）：78-82.

[6] 夏明飛.考虑服务半径约束的带预见性竞争选址问题研究[D].北京：清华大学，2015.