一种改进的模拟退火萤火虫混合算法求解0/1背包问题

任静敏，潘大志

(西华师范大学数学与信息学院，四川南充 637000)

0 引言

背包问题(knapsack problem，KP)[1]是运筹学中典型的组合优化问题，即给定n个物品的重量和价值，选择一组物品，使其总重量不超过给定的背包容量，并得到尽可能大的总价值.模型广泛运用于资本预算、负荷问题、资源配置、项目选择实际问题中.目前解决背包问题有两类方法：精确算法和启发式算法，其中精确算法有分支界定法、动态规划法、回溯法、割平面法等，精确算法能求得问题的最优解，但往往时间成本过大，占有内存较大.启发式算法的出现有效的提高了这些问题的求解效率.随着启发式算法不断被研究和改进，求解背包问题在求解时间和求解精度上取得平衡，目前的启发式算法有遗传算法[2]、蚁群算法[3]、粒子群算法[4]、人工鱼群算法[5]、萤火虫算法[6]等.

此前已有学者将萤火虫算法、模拟退火算法等用于求解一些实际问题.例如，候聪亚等[7]将振荡权重函数和模拟退火算法引入到萤火虫算法中,抑制萤火虫算法在极值点区域出现无规则的振荡现象,并将改进后的算法用于对桥式起重机箱型主梁优化.罗天洪等[8]提出一种基于时变萤火虫群优化算法，该算法根据萤火虫与邻域内所有萤火虫个体间的最小距离改变而时变步长，引入Boltzman选择机制，实时动态调整搜索过程中的移动方向与位置，增强了算法的动态适应性，改进后的算法用于平面冗余机器人手臂运动学逆解问题求解，表现出很好的稳定性.陆屹等[9]提出针对专配序列规划问题的人工萤火虫算法，为了防止算法早熟，加入模拟退火算法对其进行改进.基于萤火虫算法具有较强的全局搜索能力，而模拟退火算法有较好的局部搜索能力的特点，本文将模拟退火算法与萤火虫算法结合用于求解0-1背包问题.在融合过程中加入基于种群密度自适应变异概率，当萤火虫过于集中时增大变异概率以提高种群的多样性.采用贪心修复算法实现不可行解的可行化，同时对模拟退火算法退火速度进行改进以减少运算时间，提高算法的运行效率.仿真实验结果表明，改进后的模拟退火萤火虫混合算法能有效的解决0-1背包问题.

1 0-1背包问题

0-1背包问题是组合优化中经典的NP问题之一，其具体描述如下：

给定n个物品和有一定重量限制的背包，其中物品i的重量为wi，价值为pi，背包的最大载重重量为V.考虑如何分配物品装入背包，使得在保证不超过背包重量限制的情况下，背包内物品价值之和最大.故0-1背包问题的数学模型如下：

(1)

(2)

其中，X=(x1,x2,...,xn)，若xi=1则表示物品i装入背包；若xi=0则表示物品i未装入背包.

2 算法思想

2.1 萤火虫算法

萤火虫算法(Firefly Algorithm，FA)是一种基于种群的元启发式算法，由xin-she yang于2009年首次提出.作为一种新型仿生群智能优化算法，萤火虫算法具有鲁棒性强、求解精度高、运算速度快等优点.根据萤火虫的行为生态学，FA采用以下三个基本规则[6]:①萤火虫是雌雄同体的，每只萤火虫都会被其他萤火虫吸引；②吸引度和亮度是一致的，亮度低的萤火虫会移向亮度高的萤火虫，当两只萤火虫之间的距离增加时，他们的吸引度和亮度就会降低，当其他萤火虫没有亮度时，萤火虫会随机移动；③萤火虫的亮度与问题的目标相关.基于以上三条规则，亮度决定萤火虫移动方向，吸引度决定萤火虫移动距离，群体中的萤火虫受更亮萤火虫吸引，根据亮度和吸引度更新自己位置，萤火虫经过多次的位置更新，最终所有个体飞行到最亮萤火虫的位置，此时即是目标函数值最优.萤火虫算法[6]具体描述如下：

(1)相对亮度：萤火虫自身亮度与目标函数值有关：

Ii=f(xi)

(3)

其中，f(xi)为第i只萤火虫所在位置对应的目标函数值.在最大化问题中，亮度高的个体吸引亮度低的个体，第i只萤火虫的相对荧光亮度为：

I(r)=I0e-γr2

(4)

其中，I0为萤火虫i的自身亮度，γ为光强吸收因子，r为两只萤火虫间的欧式距离.

(2)荧光在传输过程中会被传输介质吸收一部分，吸引度大小受光强吸收因子影响，萤火虫间的吸引度为：

β(r)=β0e-γr2

(5)

其中，β0为萤火虫在距离r=0时的吸引度，γ为光强吸收因子，r为两只萤火虫间的欧式距离.

(3)初始萤火虫会被随机分配于搜索空间的任意位置.每只萤火虫代表一个可行解并随机分布于搜索空间内，对于一个D维搜索空间，设置种群个数为n，第i只萤火虫的位置表示为xi=(xi1,xi2,…,xin)，其位置更新公式为：

(6)

(7)

(8)

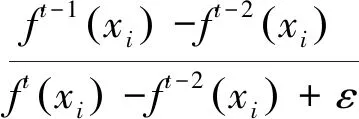
2.2 模拟退火算法

模拟退火算法(Simulated Annealing,SA)[10]由Metropolis等人于1953年提出来，随后Kirkpatrick于1983年将其用于求解组合优化问题.模拟退火的算法思想来源于固体退火这一物理过程，将固体加热至高温，再使其自然冷却.当固体温度很高的时候，其内能较大，固体内部的粒子运动处于快速且无序的状态，随着温度慢慢降低，固体的内能减小，粒子的运动逐渐趋于平稳，最后，当固体冷却到平衡温度时，内能最小且不再波动，粒子的状态最为稳定.下面是模拟退火机制的原理：

(9)

由于0-1背包问题是有约束的最优化问题，所以本文采用了文献[11]中的扩充Metropolis准则：

(10)

其中m为当前个体重量，Δm为当前个体与新个体的重量差值，ΔE为新个体与当前个体的适应度差值.T为当前温度，本文采用文献[12]中的快速退火算法，快速退火算法(VFSA)是由Ingber提出的一种降温方法：

Ti=T0*Ki

(11)

其中i退火次数，T0为初始温度，K∈(0,1)，本文设置K=0.95.

2.3 自适应变异操作

遗传算法中针对染色体实行变异操作可增强全局搜索能力，变异算子目前有单点变异，多点变异，以及自适应变异等[13].本文提出一种基于个体密度的自适应变异概率，在此概率的基础上基于两个个体间的Manhattan距离实行两点变异.种群内密度较大时说明个体过于集中，需要增大变异概率以此提高种群多样性.当密度较小时种群内个体较离散，减小种群变异概率以保护优秀个体免受破坏.

对于个体i与种群内其他个体的平均Manhattan距离为公式(12)所示，个体i与种群内最好个体的Manhattan距离为公式(13)所示:

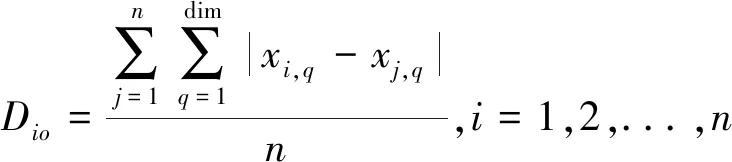
(12)

(13)

其中，n为种群规模，dim为解的维度，xi、xj、xbest分别是萤火虫种群内的个体i、个体j和最好适应度个体.萤火虫i的密度函数：

(14)

其中，count为萤火虫i到群体内所有个体的Manhattan距离小于萤火虫i到最好个体的Manhattan距离的个数.

自适应变异概率：

(15)

其中，crowd是常数，表示为个体i的拥挤程度，通常crowd∈(0,1).pmmax、pmmin分别是最大和最小变异概率，fi、fbest、fiavg分别为个体i适应度值、种群内最好个体适应度值和此时种群平均适应度值，ε为一个特别小的数，目的是防止分数无意义，本文取值ε=e-10.

当ρi

根据自适应变异概率确定对个体i是否采取变异操作，本文的变异操作是两点变异，即对个体内随机选取两个点，对两点间部分采用0变1、1变0的操作.

2.4 编码方式

由于0-1背包问题是离散问题，而萤火虫算法的寻优过程是连续的，所以需要将解空间内的连续解离散化，假设连续空间内的解为Xi={xi1,xi2,…,xiD},(i=1,2,…,n)，其中xij∈(-1,1),(i=1,2,…,n;j=1,2,…,D)，转化为离散空间内的解为Yi={yi1,yi2,…,yiD}.本文采用以下编码方式：

(16)

3 模拟退火萤火虫混合算法求解0-1背包问题的具体实现

根据改进后的算法策略，构造了求解0-1背包问题的模拟退火萤火虫混合算法(GMFS)，改进算法的具体步骤如下：

Step1：设置算法相关参数，种群大小n，光强吸收因子γ，萤火虫吸引度β，最大变异概率pmmax，最小变异概率pmmin，初始温度T0，终止温度Tfinal，马尔科夫链长度Lchain，快速降温系数K，随机初始化种群.

Step2：令T=T0，利用贪心算法对初始种群的不可行解进行修复.

Step3：当T

Step4：若L

Step5：利用贪心算法对新种群的不可行解进行修复，计算新解与旧解的能量差值，若差值为正则更新解；否则，以一定概率接受新解.

Step6：计算当前温度T，计算并更新全局最优值和最优解.

Step7：对种群内个体根据改进变异概率判断是否进行变异操作，并同时对不可行解作修复处理.转Step3.

GMFS算法流程图如图1所示：

图1 GMFS算法流程图Fig.1 The flow diagram of GMFS

4 仿真实验

为了验证本文提出的GMFS算法的有效性，文章选用三组算例，背包内物品个数分别为20个，50个，100个.其中20个物品和50个物品的背包问题实验数据来源[14], 100个物品的背包问题实验数据来源[15]，每次实验独立运行30次.同组对比实验的算法AGAA来源于文献[16]，加入贪心修复的萤火虫算法FA来源于文献[17]，贪心模拟退火算法来源于文献[11].

本文仿真实验所用硬件环境为处理器：AMD A6-3420M APU with Radeon(tm) HD Graphics 1.50 GHz，安装内存：4.0GB，系统类型64位操作系统，操作系统：Windows 7旗舰版.集成开发环境：MATLAB R2014b.下面对本文算法GMFS以及四个对比算法(AGAA，FA，SA，SAFA)进行参数设置，详情见表1.其中Pc,Pm分别为交叉概率和变异概率，Tini,Tfin分别为初始温度和终止温度，L为markov链，K为退火参数，popsize为种群规模，maxgen为最大迭代次数，β0为最大吸引度，γ为介质吸收因子，α为步长因子.

表1 求解0-1背包问题的四种算法参数设置Tab.1 Parameter settings of 4 algorithms to solve the 0-1 knapsack problem

对三组算例分别独立运行30次，测试结果分别与理论最优值进行对比，比较30次测试结果，得出各个算法的最优解，最差解和成功次数，并根据所得数据计算其平均值，标准差，偏差和改进比例.运行结果见表2，其中平均值和最优值可看出算法的寻优能力，标准差可以反映算法的鲁棒性，偏差能衡量算法的稳定程度，偏差公式为：

偏差=(目标最优值-平均值)/目标最优值

改进比例对比本文算法，其他三种算法的改进程度，改进比例公式为：

改进比例=(改进算法最优值-其他算法最优值)/其他算法最优值

表2 4种算法所获得统计值比较Tab.2 Statistic comparison of 4 algorithms

续表1：

N算法最优解最差解平均值成功次数偏差/%标准差改进比例/%50AGAA30983007306703.0920.640.16SA30132933296004.6029.732.98FA30953050307001.0612.230.26SAFA30903075308600.132.880.42GMFS3103310331033000-100AGAA79197453770003.94117.431.22SA79247621782702.3666.011.16FA74737070724309.6496.507.27SAFA80167991800160.191.700GMFS8016801680163000-

图2 算例1中各算法的收敛结果Fig.2 Different algorithm convergence in example 1图3 算例2中各算法的收敛结果Fig.3 Different algorithm convergence in example 2图4 算例3中各算法的收敛结果Fig.4 Different algorithm convergence in example 3

通过对以上数据的对比观察，可以看出，当物品个数为20时，SA、AGAA、GMFS、SAFA都能达到最优解，且SA的成功次数等于本文算法，反映了SA对于低维背包的搜索能力很强，但是从图2中可以看出SA与AGAA的收敛速度不及GMFS.当物品个数为50时，GMFS在第4代时就找到全局最优值，而SA、SAFA与AGAA均未能在100代内搜索到，且此时SA的标准差与偏差数值都较大，说明当选择物品个数较多时，GMFS能快速且精准的搜索到全局最优.当物品个数为100时，通过表2和图4可看出，GMFS在退火次数30代内即能搜寻到全局最优值，相对其他三种算法的改进比例较大.SAFA虽然在30次独立实验中有6次找到最优值，但收敛速度慢，且精确度不高.SA与AGAA的偏差和标准差数值偏大，且都陷入了局部最优，相对本文算法其爬行能力较弱，全局搜索能力不强.而FA在三次算例中均未找寻到全局最优，这与萤火虫算法自身局部搜索能力较弱有关系.仿真实验表明，GMFS具有全局搜索能力强，收敛速度快等优点.

5 总结

本文算法GMFS在三次算例中都能很快搜寻到全局最优，得益于改进后的变异操作，增加其全局搜索能力，通过萤火虫算法找寻新解与模拟退火算法选择新解，在一定程度上保留了种群多样性和当前最优解，贪心算法的加入减小了种群内解的损失，同时加快收敛到全局最优值的速度.说明本文算法能有效求解0-1背包问题，是一种性能较好，鲁棒性强的算法.