注浆加固对改善衬砌受力及变形的效果研究

2020-03-02李文键

福建交通科技 2020年1期

■李文键

(宁德屏古高速公路有限责任公司，宁德 352200)

0 前言

在破碎、软弱围岩地段修建隧道，除了增大支护结构的厚度及强度，对围岩进行注浆加固也是一种十分有效辅助施工手段[1,2]。注浆不仅可以改变围岩的力学性能，提高围岩的力学参数，减小其渗透系数，提高自身的稳定能力，同时施工工艺简单，施工作业空间要求较小，参数可以随时调整。此外，对于出现严重渗漏、衬砌开裂的隧道，如果拆除二衬返工，除了拖延工期，还可能造成次生病害；在二衬表面进行黏钢加固，会一定程度的影响隧道的外观；而衬砌背后注浆能有效避免这些问题。为了定量分析注浆加固对围岩和隧道的影响，本文以某两车道隧道局部存在二次衬砌厚度不足这一事实为例，利用有限元软件建立二维数值计算模型，对比注浆加固前后围岩与支撑结构应力及位移变化情况，得出其加固效率，得到的结论可为隧道病害治理提供借鉴意义。

1 模型建立

某隧道YK229+020(±5m)段落位于进口Ⅴ级围岩浅埋段，采用ZDK-1 型复合支护，二次衬砌厚度为55cm，配筋为每延米对称配筋单侧5φ25(24.54cm2)。地形基本无偏压，覆盖层较薄，为坡积粘土及残积粘性土。二衬内轮廓采用隧道激光断面仪检测，厚度参照雷达检测取值，计算采用厚度如表1 所示。

在考虑注浆加固效果时，采用地层-结构分析法[3]能更好反映围岩与隧道结构协调变形情况，很好显示隧道结构和围岩共同受力与变形。模型边界尺寸取隧道直径5 倍，采用实体二维平面应变模型。围岩用Mohr-Coulomb模型，采用4 节点的平面应变单元；二次衬砌用线弹性模型，采用两节点的线性梁单元。由于分析对象为二次衬砌，为了建模方便又不失正确性，通过直接提高洞身围岩参数的方法模拟初期支护对围岩的加固效果。该计算模型仅考虑围岩和衬砌自重。围岩及注浆加固具体的物理计算参数(根据地质勘察资料和规范确定)见表2。

表1 二衬厚度表/cm

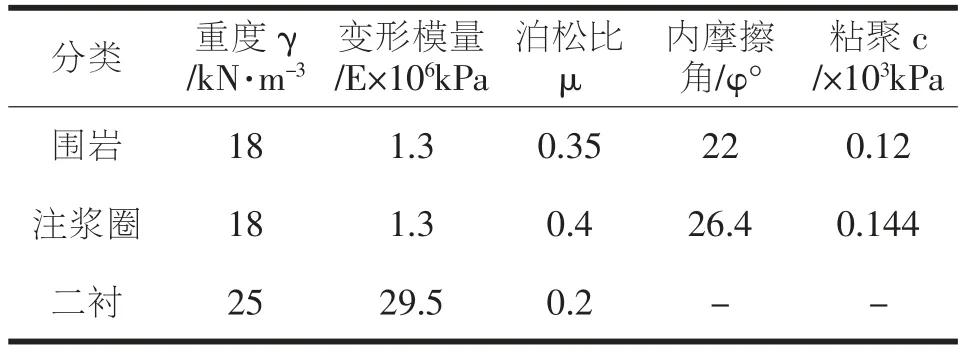
表2 计算参数

2 注浆加固范围的数值模拟分析

在同一埋深(h=25m)条件下，计算工况分加固圈0m(也即未加固)，1m、3m，5m 和7m 五个工况。加固圈为5m的模型示例如图1 所示，加固圈内以提高围岩参数来模拟注浆加固效果。

图1 注浆加固模型示例

2.1 衬砌内力分析

图2 是未加固和加固5m 两种计算工况的衬砌轴力ESF1(单位kN，下同)和弯矩SM1(单位kN·m，下同)计算结果示意图。

从轴力图可知：(1)衬砌处于受压状态，且在拱腰部位轴力值较大；(2)随着加固范围的增大，拱腰和仰供部位轴力值逐渐降低。从弯矩图可知：(1)负弯矩最大值出现在拱脚部位，拱脚部位受压；(2)仰拱部位则分布正弯矩，表明仰拱受拉，这是因为仰拱向上隆起导致受拉；(3)弯矩值随着加固范围的增大，而逐步减小。

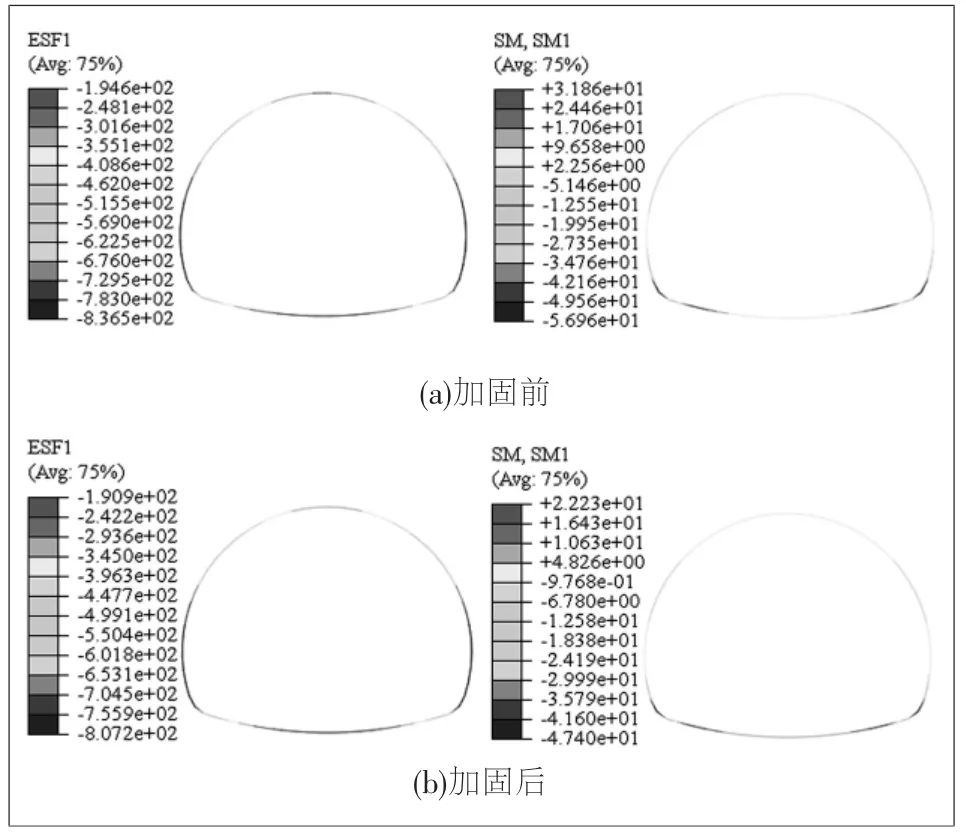
图2 5m 注浆加固前后衬砌轴力和弯矩等值云图

2.2 围岩应力分析

图3 为未加固和加固5m 计算工况的围岩和相应衬砌的Mises 应力(单位kPa，下同)云图示意图。从图中可知，加固后围岩自身应力增加，反观衬砌的应力减小。这主要是由于围岩强度增加，自身承载力增加，增加了自身稳定性，隧道由于开挖而产生的释放应力由于围岩强度增加而承担能力增加。换言之，注浆加固后围岩越稳固，支护结构受力越小，隧道越安全。这也与围岩级别对隧道的影响得到的结论一致。

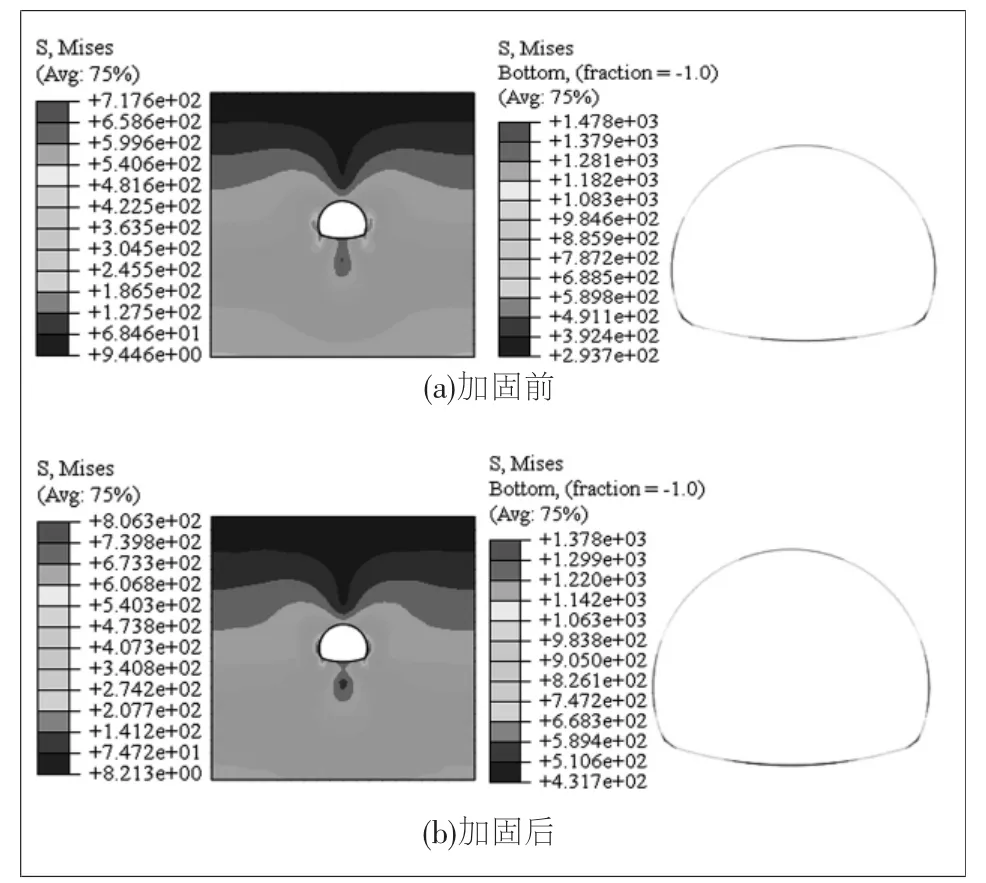
图3 5m 注浆圈加固前后Mises 应力等值云

2.3 注浆加固效率分析

本文采用公式(1)计算注浆加固效率：

式中： ΔD——表示注浆前隧道位移值，mm；

ΔD*——表示注浆加固后隧道位移值，mm；

λ——表示加固效率。

表3 是五个工况下位移的计算结果，其中水平位移为两侧拱腰部位的水平位移值之和(下同)。括号内数值是采用公式(1)计算出的加固效率，其与加固范围大小的关系曲线如图4 所示。

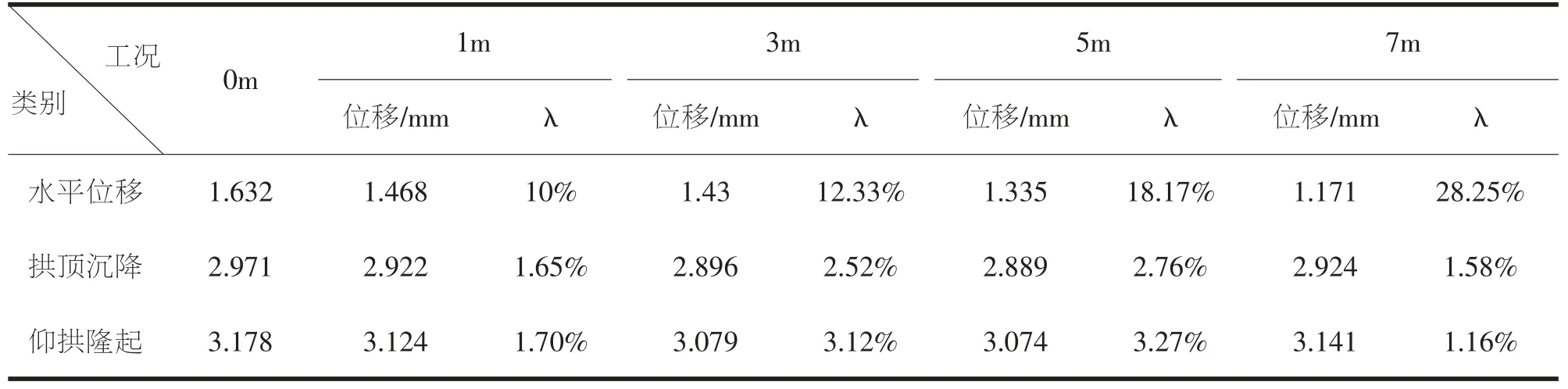
表3 五个计算工况位移值与加固效率比较

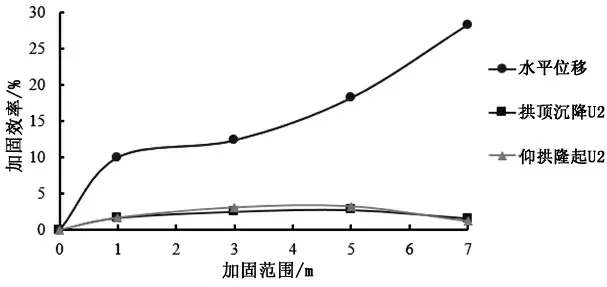
图4 加固效率与加固范围关系曲线

从图4 可知，抵抗水平位移的加固效率随着加固范围增大而增加，且抵抗水平位移的加固效率大于同条件下的竖向位移的加固效率。抵抗拱顶沉降和仰拱隆起的加固效率在5m 范围内，随着加固范围增大而增大，但大于5m 后，加固效率反而减小。分析计算过程，可认为主要由于注浆的泊松比大于围岩的泊松比所引起。根据计算结果结合工程实践，建议注浆加固范围不宜超过5m，以4m 为最佳注浆范围。

3 隧道埋深对注浆加固影响

为了分析埋深对注浆加固的影响，本文取隧道埋深取0m、10m，20m，30m 和40m 四个工况，同时考虑注浆范围一般为3～8m，因此计算表4 所示的28 种工况。

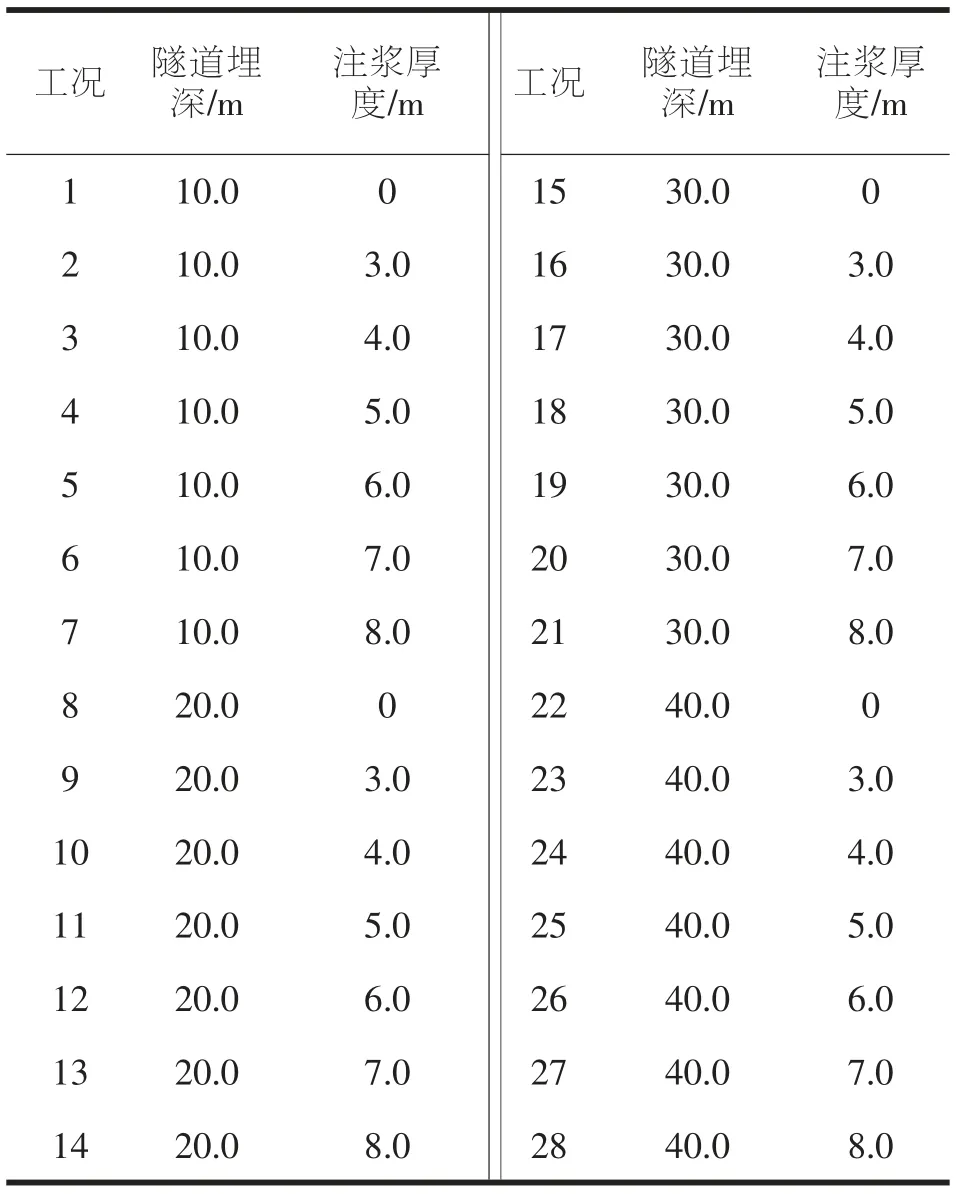
表4 不同埋深与注浆厚度的组合工况

3.1 衬砌内力分析

图5 是加固范围为5m、埋深10m 和40m 两种工况的衬砌轴力ESF1 和弯矩SM1 等值云图。从图中可知，轴力和弯矩分布规律一致，也即埋深对轴力和弯矩分布规律影响不大；但随着埋深增加，轴力和弯矩值增大。

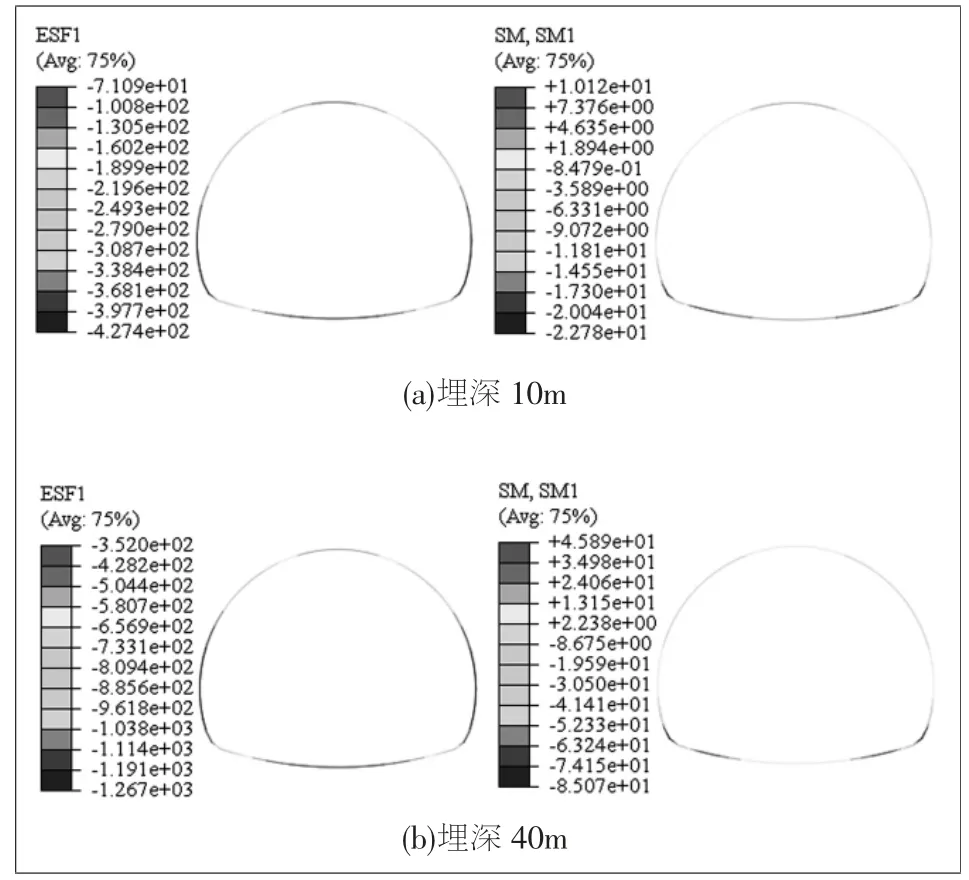
图5 衬砌轴力和弯矩等值云图

图6 是轴力和弯矩最大值随隧道埋深变化的规律。可知，隧道埋深与拱墙部位的轴力和弯矩值基本呈线性关系，且从直线的斜率可知，埋深对仰拱部位的轴力影响大于对拱腰部位的影响。

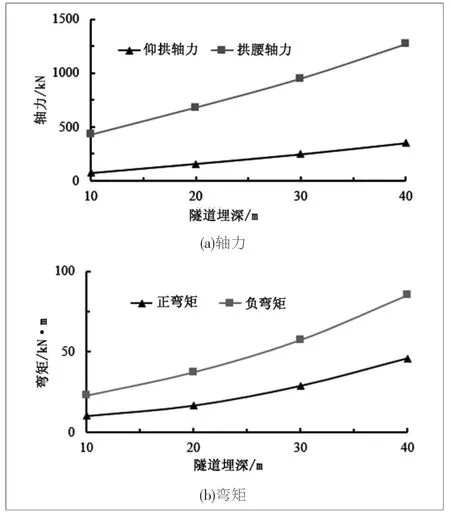
图6 加固后内力隧道埋深关系曲线

3.2 围岩应力分析

图7 是埋深10m 和40m 两种工况围岩的Mises 应力云图。可知加固范围一致，也即在其它条件一样的情况下，隧道埋深越深，围岩应力越大，衬砌承载的作用力也越大，也即对支护结构的要求越高。

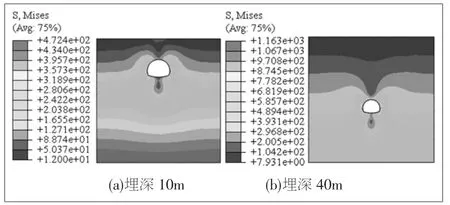
图7 围岩Mises 应力等值云(单位:kPa)

3.3 注浆加固效率分析

根据计算结果，提取出28 种工况的水平位移、拱顶沉降和仰拱隆起值，同时根据公式(1)计算加固效率，并分别绘制了水平位移、拱顶沉降和仰拱隆起相应的加固效率与隧道埋深的关系曲线，如图8 所示。

图8 不同部位位移的加固效率与隧道埋深关系曲线

从图8 可知，水平位移的加固效率随埋深增加而增大，分布规律一致，即表明注浆加固范围对分布规律不产生影响；隧道埋深小于20m 时，加固范围对加固效率幅度变化影响较大，而当大于20m 时，影响减小；埋深越大，同一埋深条件下，加固效率最大；从曲线发展趋势可知，当埋深达到一定值后，不同的加固范围的加固效率趋于一致，也即加固厚度对加固效率基本不产生影响。