积累数学基本活动经验的策略探索——《估计不规则图形的面积》教学分析与思考

文/广州市荔湾区教育发展研究院

“数学基本活动经验”作为《义务教育数学课程标准(2011年版)》提出的“四基”之一，内涵丰富。人教版2013年版教科书五年级“多边形的面积”单元，《估计不规则图形的面积》是新增的内容，旨在让学生在解决不规则图形的面积的过程中，灵活运用各种策略与方法估计图形的面积，从而培养学生的估算意识，体会估算策略和方法的多样性，积累数学活动经验。笔者尝试从这一课的主要环节入手进行分析，探讨在教学中如何帮助学生积累数学基本活动经验。

一、回忆方法，激活已有的数学活动经验

任何数学学习活动都与一定的知识背景相联系。学生在学习新的解决问题的策略时，必须要以已有的解决问题的经验为基础，同时在新问题与旧经验之间建构起意义上的联系。这样，学生在学习新策略时，才能灵活地将一些已有的经验进行迁移。本课要估计不规则图形的面积，需要借助前几节课的知识经验，即推导平行四边形、三角形、梯形的面积计算公式时数方格和转化的方法。因此，首先引导学生复习旧知，由旧引新：

1.复习公式：我们学过哪些图形的面积计算公式？分别是什么？

2.回忆方法：推导这些图形的面积计算公式时，我们用了哪些方法？

这样，不仅帮助学生复习已学过的长方形、正方形、平行四边形、三角形、梯形的面积计算公式，还引导学生回忆推导这些面积公式用到了数方格和转化的方法，激活学生已有的数学活动经验，搭建起通往新知的“桥梁”。

二、激活思维，引发新的数学活动经验

不管哪种数学活动经验，其形成与积累都离不开重要的载体——数学实践活动。但从数学活动经验的角度来看，不是有数学活动就能成为学生的经验，在数学活动中要有思维投入、情感态度的体验和感悟。如何让学生的思维自觉参与进来?这需要提出好的问题，激活学生的思维。因此在本课的两个探究环节精心设问：

1. 通过数方格估计不规则图形的面积的“确定标准”环节

面积是1dm2的方格纸面积单位是1cm2的方格纸

面积单位是0.25cm2的方格纸

(1)设问：观察上面三幅图，你认为使用面积单位是多少的方格纸估计这片叶子的大小更精确？

(2)设问：根据这片叶子的大小，你认为使用面积单位是多少的方格纸进行估计比较合适？

学生通过数方格推导长方形、平行四边形的面积公式时，已有的数学活动经验是用面积单位是1cm2的方格纸(教材提供)。而现在估计不规则图形的面积，估算策略的关键是要为估计的事物找到一个合适的测量标准。因此在“确定标准”环节，提供三种测量标准的方格纸，提出两个关键问题。通过不断对比、反思，使学生的思维不断被激活，引发出新的数学活动经验：测量不规则物体时，单位越小，估计结果越精确，但不一定是最合适的，要根据测量物体的面积选择适合的测量标准。例如这片叶子比较小，选择面积单位是1cm2的方格纸进行估计比较适合。

2. 通过转化的方法估计不规则图形的面积的“指导方法”环节

设问：上面三种转化成平行四边形的方法，哪种方法更合理？为什么？

学生推导平行四边形、三角形、梯形面积公式时，把新的图形转化为已学过的图形时，已有的数学活动经验是等积变形。而现在把不规则图形转为规则图形的关键是接近、合理就行。因此本课在转化的关键处，提供三种转化的方法，通过对比、反思，使学生明确不规则图形转化为规则图形时，要注意接近、合理，并以此为契机，指导学生转化的技巧。从而把原来规则图形转化的经验“割补”转化为“看轮廓想图形，定点、定边”，使学生新生成的数学活动经验很自然地嵌入原有的经验系统。

三、自主探究，经历活动经验形成的深刻体验

没有亲身经历就不可能获得真正意义上的体验。这就需要教师以学生的经验为起点，积极创设基于学生数学学习所需要的活动情景，调动他们已有的知识经验，促使他们积极主动参与数学活动。因此，本课的探究环节，充分让学生自主探究，经历活动经验形成的深刻体验：

1.通过数方格估计不规则图形面积的探究环节。首先引导学生确定标准，提供三种测量标准的方格纸，通过对比、反思，得出叶子比较小，选择面积单位是1cm2的方格纸进行估计比较适合。接着让学生独立探究(学生操作约5分钟)，再确定范围，引导学生思考：这片叶子的面积大约会是多少但又不会超过多少？然后交流方法，让学生展示自己的估计过程。最后反思方法：刚才我们用什么方法来估计叶子的面积？在使用这个方法的时候需要注意哪些问题？

2.通过转化的方法估计不规则图形面积的探究环节。首先引导转化：这片叶子是不规则图形，没有现成的公式求不规则图形的面积，怎么办呢？接着让学生独立探究(学生操作约5分钟)，再交流方法，让学生展示自己的转化、估计过程。然后指导方法，提供三种转化的方法，通过对比、反思，使学生明确不规则图形转化为规则图形时，要注意接近、合理，并以此为契机，指导学生转化的技巧是“看轮廓想图形，定点、定边”。最后反思方法：在使用转化方法的时候需要注意哪些问题？

这两个教学环节环环紧扣、层层递进，教师都留有充足的时间和空间，让学生积极、主动地经历探究、交流、内化、反思等数学活动的全过程，从而获得数方格和转化的深刻体验，让学生在活动中不知不觉地积累新的数学活动经验。

四、回顾反思，积累新的数学活动经验

数学活动经验的获得首先是基于活动的，但经历了并不等于积累了经验，如何从“经历”走向“经验”，这就要求学生对所获得的数学活动经验加以反思、提炼。如本课的学习，学生的主要任务是体会估算策略和方法的多样性。因此，在每一个教学环节结束时，要适时引导学生回顾反思：刚才我们用哪些方法来解决这个问题？哪种方法比较好？为什么？在使用这个方法的时候需要注意哪些问题？一方面是引导学生体会估算的方法，另一方面是让学生反思积累数学活动的经验。通过多次对比梳理，学生进一步感受用转化的方法估计不规则图形的面积是一种比较简便的估算策略，并将这一策略逐步积累成深层次的经验。

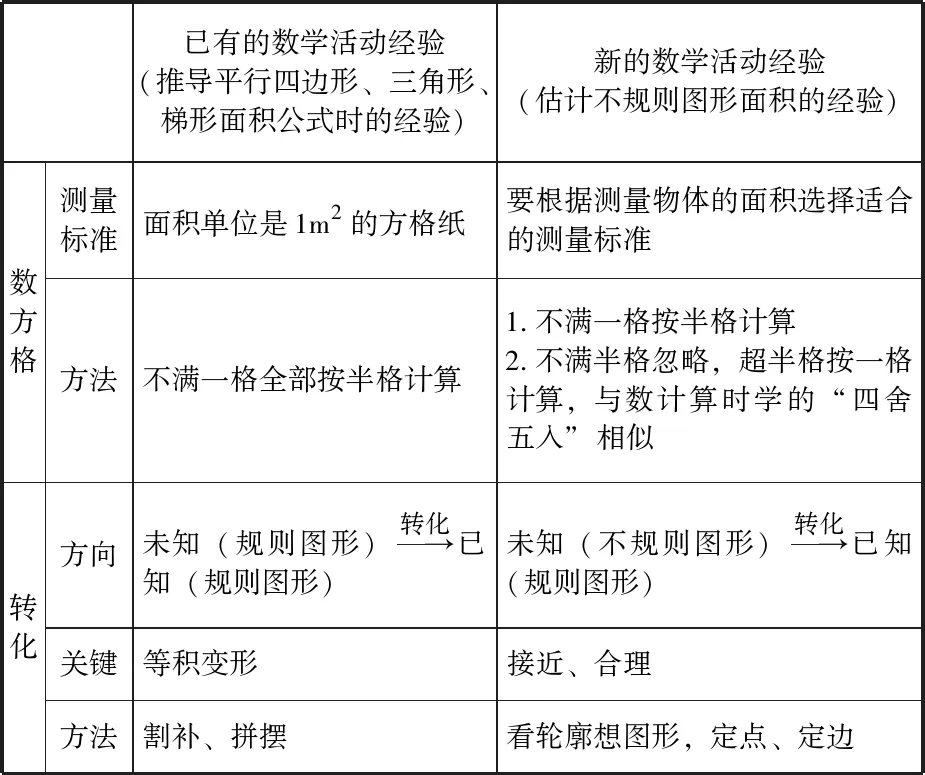
已有的数学活动经验(推导平行四边形、三角形、梯形面积公式时的经验) 新的数学活动经验 (估计不规则图形面积的经验)数方格测量标准面积单位是1m2的方格纸要根据测量物体的面积选择适合的测量标准方法不满一格全部按半格计算1.不满一格按半格计算2.不满半格忽略,超半格按一格计算,与数计算时学的“四舍五入”相似转化方向未知(规则图形) 转化 →已知(规则图形)未知(不规则图形) 转化 →已知(规则图形)关键 等积变形接近、合理方法 割补、拼摆看轮廓想图形,定点、定边

积累解决问题的经验是一个循序渐进的过程。学生通过反思自己参与数学活动过程中的所得所想，可以将较低层次的活动经验上升到一个更高的水平，实现经验的转化或重组，并逐步生成新的经验。如本课引领学生经历了估测不规则图形叶子的全过程——由旧经验的激活到新问题解决经验的形成。使学生在灵活运用已有活动经验的基础上大胆践行、探索，亲历估算的全过程，使他们获得了个性化的感受和体验，再次开发新的活动经验，通过反思积淀，积累了深层次的活动经验。