基于有限元法的空调换热管的塑性失稳分析
2020-03-02岳建军
岳建军
(英格索兰亚太工程技术中心,江苏 太仓215400)
0 引 言
在工程设备和结构中存在着许多受压构件,对这些受压构件的设计校核不仅要进行强度(应力)和刚度(变形)的计算,往往还要进行稳定性计算(也称为屈曲分析)。为了节省材料和减轻质量,宽长薄壁结构和细长杆状结构在工程设计中得以广泛应用,在受压状态下,这类结构经常因为结构失稳而导致失效或破坏,并非因为结构强度不够或者刚度不足。历史上也存在不少由于结构失稳而导致的重大事故:1907年发生的加拿大魁北克省劳伦斯河上的魁北克桥的倒塌事故就是由于该桥梁的悬臂下弦在受压作用失稳所致;1987年发生在美国哈特福德市的一座体育馆网架屋顶坍塌事故则是由于钢屋架结构发生压杆屈曲而导致的。结构失稳会导致构件突然丧失承压能力而发生整体或局部垮塌,这种破坏有可能是灾难性的。因此,研究结构的稳定性问题,对受压构件进行屈曲分析是工程结构设计校核的主要任务之一。
工程中常见的结构失稳包括压杆失稳[1],以及薄板、薄壳的受压失稳[2]。例如在内压作用下的圆柱形薄壳,壁内应力为拉应力,这就是一个强度问题,比如商用空调机组的管壳式换热器(如图1)的圆筒形壳体的强度校核。但如果圆柱形薄壳受到了均匀外压的作用,此时壁内应力变成了压应力,则当外压达到某一临界值时,薄壳的圆形平衡就变为不稳定,这就是外压作用下的薄壳失稳问题,比如管壳式换热器中的换热管会受到制冷剂的外压作用,在设计时候就需要考虑其稳定性问题[3]。

图1 管壳式换热器
在工程计算时,要评估结构在载荷作用下的失稳风险,可以先进行线性屈曲分析(或称特征值屈曲分析),线性屈曲分析可以预测结构在失稳或塌陷之前所能承受的最大荷载(或称临界载荷)。基于有限元模型的特征值分析不仅可以得到屈曲载荷,还可以显示相应的失稳模态,该方法分析简单,计算速度快。但特征值屈曲分析基于线弹性理论,其往往产生非保守的结果,计算得到的临界载荷要高于实际情况。因此,在实际工程结构分析中一般不采用特征值屈曲分析,但特征值屈曲分析可以作为非线性屈曲分析的初步评估。
在实际的工程应用中,结构在外力作用下往往会经历材料的非线性或边界的非线性过程,而结构本身也可能存在初始几何缺陷,因此要研究此情况下的结构失稳问题,就需要进行非线性屈曲分析。非线性屈曲分析基于非线性静力学分析,在计算时随着荷载的逐渐增加来寻找结构失稳的荷载水平,直到求解过程开始趋于发散为止[4],如图2所示。计算模型中可以包括结构的初始几何缺陷、材料的塑性行为、边界条件的非线性及大挠度响应等特征[5-7]。基于弹塑性材料的非线性屈曲分析还可以模拟结构的塑性失稳,即构件在载荷作用下在整体上或某一局部的全厚度上发生过度塑性变形而不能保持原有形状的一种失稳的失效形式。例如受外压的薄壳(如前文提到的管壳式换热器中的换热铜管)在外压较大时会被压溃。
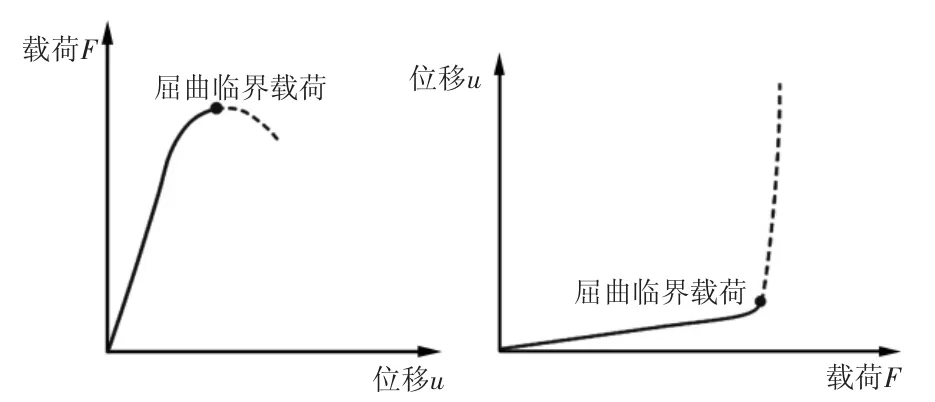
图2 非线性屈曲分析载荷-位移(挠度)曲线
1 基于有限元法的非线性屈曲分析
1.1 算例
本文以某一长度为200 mm、外径为26 mm、内径为24 mm、壁厚为1 mm的薄壁圆管为例(如图3),假设的边界条件为两端刚性固定,受均匀外压作用,并给定材料的弹性模量为2×105MPa,泊松比为0.3。运用大型商用有限元分析软件ANSYS Workbench进行非线性屈曲分析,通过给定不同的几何初始缺陷、不同的材料屈服强度及弹塑性材料模型来分析研究几何初始缺陷、材料的屈服强度及塑性硬化对结构失稳的临界载荷的影响。

图3 薄壁圆管算例
1.2 结果分析
1.2.1 初始几何缺陷对屈曲临界载荷的影响
在该算例中,分析时采用双线性随动硬化的弹塑性材料模型, 并假定材料的屈曲应力(以Ys表示)为200 MPa,塑性硬化阶段材料的切线模量(以Et表示)为1500 MPa。需要说明的是,初始几何缺陷系数的施加需基于ANSYS Workbench特征值屈曲分析的计算结果,特征值屈曲分析结果的第一阶屈曲模态如图4所示。
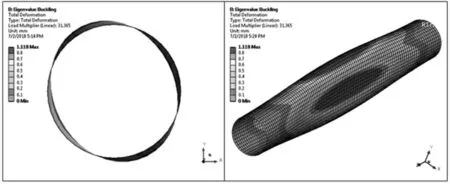
图4 线性屈曲分析结果(第一阶屈曲模态)
由图4可知,该屈曲模态的最大位移约为1.12 mm,圆管的初始几何缺陷可以通过缺陷系数乘以线性屈曲模态位移来施加。比如定义缺陷系数为0.1,其对应的最大初始缺陷为0.112 mm。
计算不同的几何缺陷系数(Defect Factor,以DF表示)下的圆管在均匀外压作用下的载荷位移曲线,如图5所示。该圆管屈曲后的结构变形如图6所示。从该曲线可以看出,随着载荷的增加,屈曲载荷位移曲线在到达某一临界点后出现突变,该突变处所对应的载荷即为结构的失稳临界载荷,在该临界点之后,随着载荷的微小增加,位移呈现急剧上升的趋势。在初始几何缺陷系数分别为0.100、0.010、0.001的情况下,该圆管的屈曲临界载荷分别为12.4、18.8、20.5 MPa。可见,改善初始几何缺陷可以有效提高结构失稳的临界载荷。同时也可以看到,当几何缺陷系数从0.01降低到0.001时,屈曲临界载荷仅从18.6 MPa增加到20.5 MPa,这说明当初始几何缺陷能够控制在足够小的范围内时,几何缺陷的进一步降低对结构失稳临界载荷的改善呈下降趋势。

图5 不同几何缺陷系数DF下的载荷位移曲线
1.2.2 材料屈服强度对屈曲临界载荷的影响
在该算例中,假定圆管的初始几何缺陷系数(以DF表示)为0.01,分析时仍采用双线性随动硬化的弹塑性材料模型,并假定塑性硬化阶段材料的切线模量Et为1500 MPa,通过给定三种不同的屈服应力水平(200、225、250 MPa)来研究材料的屈服强度对屈曲临界载荷的影响。
计算不同的材料屈服强度Ys下的圆管在均匀外压作用下的载荷位移曲线如图7所示。

图6 圆管屈曲后的结构变形

图7 不同材料屈服强度Ys下的载荷位移曲线
从图7可以看出,在材料的屈服强度分别为200、225、250 MPa的情况下,该圆管的屈曲临界载荷分别为18.8、20.8、22.5 MPa。由此可见,由于材料屈服强度的提高,使得结构的承载能力更强,结构失稳的临界载荷也会相应增大。
1.2.3 材料应变硬化对屈曲临界载荷的影响
塑性材料在超过屈服阶段之后,此时材料应力将会随着应变的增大而不断加大,这说明材料又恢复了抵抗变形的能力,要使其继续变形,就必须增加载荷,这一现象称为材料的强化(或称应变硬化)[1]。材料经过应变硬化阶段后其屈服强度得以提高,根据1.2.2节的计算结果可以看出,经过材料应变硬化过程的结构,其抵抗失稳的能力也会得以提高。
材料在屈服之后,应力应变曲线呈现非线性。在进行工程分析时,通常需要对应力应变曲线进行简化,如前述的双线性随动硬化的弹塑性模型,将塑性应变硬化阶段用直线代替,其对应的斜率以切线模量Et来表征,这样与弹性阶段(对应的斜率为材料的弹性模量E)共同组成一个双线性的材料本构关系,如图8所示。
在实际工程应用中,某些材料在屈服后有明显的屈服流动阶段,当屈服流动阶段比较长或者硬化程度比较小时可以忽略,这时可以简化为理想弹塑性材料模型[8],即应力达到屈服点之前,应力应变呈线性关系,应力达到屈服点之后,应力保持为常数σs。此时对应的切线模量Et=0。在本算例中,假定圆管的初始几何缺陷系数(以DF表示)为0.01,并假定材料的屈服强度(以Ys表示)为200 MPa,通过给定三种不同的切线模量(0、1500、3000 MPa)来研究材料的塑性应变硬化阶段的材料切线模量对屈曲临界载荷的影响。
计算不同的材料塑性应变硬化阶段的切线模量Et下的圆管在均匀外压作用下的载荷位移曲线如图9所示。

图8 材料拉伸应力应变简化曲线

图9 不同材料切线模量Et 下的载荷位移曲线
从图9可以看出,在材料的切线模量分别为0(即理想弹塑性材料)、1500、3000 MPa的情况下,该圆管的屈曲临界载荷分别为18.6、18.8、19.1 MPa。由此可见,由于材料切线模量的增大(通常体现在材料具有更高的抗拉强度或更小的延伸率和韧性),材料呈现更短的屈服流动阶段及更大的塑性硬化程度,结构失稳的临界载荷也会相应增大。
1.3 实际案例
结合以上分析,对某实际空调产品中的换热管设计进行了有限元仿真计算。在实际应用中,为了增加换热管的换热面积,提高换热效果,通常采用的是螺旋翅片管(包括光管段、过渡段及翅片段),如图10所示。
尽管在翅片加工时由于材料的挤压变形,导致翅片段的最小壁厚小于光管段,但在有限元分析时候,考虑到翅片加工时材料的应变硬化行为,翅片段材料的屈服强度得以提高,其抵抗失稳的载荷反而要高于光管段和过渡段,这也与实验结果相吻合。实际的高效换热管的样件测试结果表明,塌陷(失稳)通常发生在光管段和过渡段。而基于有限元分析得到结构发生失稳时的临界载荷与试验结果也十分接近(如表1)。

图10 螺旋翅片换热管
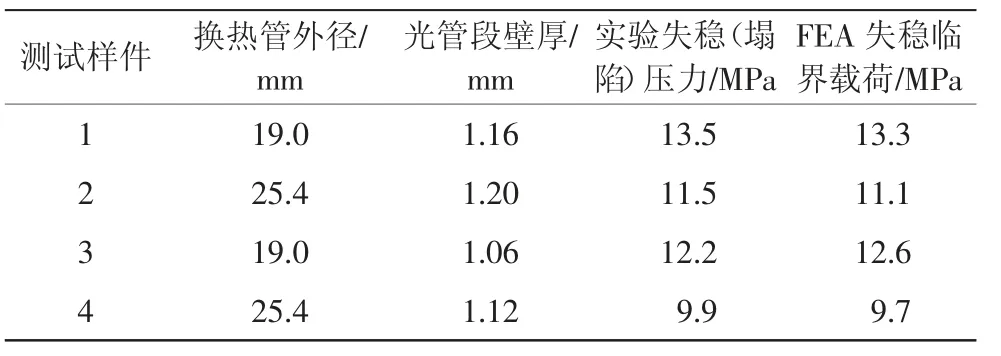
表1 实验失稳压力与FEA计算结果对比
2 结 论
相比于线性特征值屈曲分析,非线性屈曲分析可以在计算模型中考虑结构的几何初始缺陷、材料的塑性行为、边界条件的非线性及大挠度响应等特征,能较好地得到结构的屈曲特性,在工程分析中越来越受到重视。考虑弹塑性材料的非线性屈曲分析还可以模拟结构的塑性失稳,从而可以进一步提高工程分析的精度。本文结合基于弹塑性材料的薄壁圆管非线性屈曲分析算例,研究了几何初始缺陷、材料的屈服强度及应变硬化对结构失稳临界载荷的影响,为空调管壳式换热器中换热管的设计提供了借鉴与指导。计算结果表明,在进行空调管壳式换热器中换热管的失稳分析时,不仅要考虑结构的初始几何缺陷,必要时还需考虑材料的弹塑性力学行为(比如翅片换热管加工时所发生的材料应变硬化行为)。在条件允许的情况下,建议通过拉伸试验得到材料的实际应力应变曲线作为有限元分析的输入,从而可以更准确地预测结构失稳的临界载荷,达到降低实验成本、优化结构设计的目的。
