双摆头型五轴数控机床的坐标变换关系研究
2020-03-02王馨李宪辉
王馨, 李宪辉
(1.山西机电职业技术学院,山西 长治046011;2.哈尔滨鑫润工业有限公司,哈尔滨150300)
0 引 言
随着装备制造业的快速发展,数控加工中心得到了广泛应用。尤其是五轴数控加工技术的出现为复杂曲面类零件的制造提供了可能。一次装夹可完成多道工序,使得数控加工在提高生产效率的同时保证了加工精度,提高了加工产品质量的稳定性,也避免了静点切削。其中,刀轴矢量驱动控制是五轴加工的特点,保证切削过程中刀位点坐标数据准确同样是五轴数控机床控制的关键。一方面,五轴机床运动模型可视为多体拓扑结构,系统末端的刀位点可看作最终的控制对象,实现运动学模型的计算与求解,完成数据转换关系是整体控制理论的核心,是五轴机床运动控制理论的基础;另一方面,数学计算后所得的数据需转换成符合特定机床运动模型及数控系统可以识别的程序代码,即后置处理。两者相结合才能实现控制机床运动、加工出符合技术要求的产品的目的。本文以C-A(X)型五轴数控加工中心结构为例,重点利用工程数学实现后置处理中运动模型数据换算,阐述双回转结构五轴机床的运动学原理。
1 后置处理在典型数控加工流程中作用
首先,在数控加工中,不同的机床由于运动模型、数控机床控制器的差异,NC程序格式也会不同;第二,使用自动编程软件得到的刀轨源文件(CLSF)是不能为数控系统所直接识取的,必须经后置处理,转换成特定机床能识别的NC代码,实现机床驱动并完成加工任务。完整的数控加工流程如图1所示,可见后置处理是连接计算机设计与机床驱动完成数控加工的桥梁,也是机床能否按照设计人员的意图加工出符合生产要求产品的关键。
一般来说,将刀具路径规划及刀轨的计算过程称为前置处理;将数学计算后所得的刀位数据转换成符合具体机床运动结构、操作系统可以识别的程序代码(即数控加工程序)的过程称为后置处理(Post Processing)[1]。我们把能够实现后置处理任务的模块称作后置处理器,内部包含机床运动模型和控制系统信息。图2是以某工艺品的加工为例,直观展示产品从设计到加工任务完成的整体流程。

图1 数控加工流程图
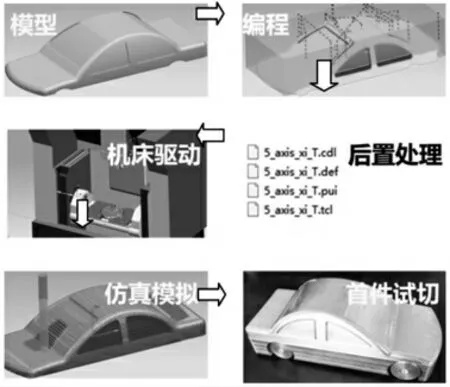
图2 数控加工任务流程
由此可以看出,后置处理的本质是提取数控加工轨迹,即刀位文源件CLSF(Cutter Location Source File)转化成刀位数据,结合特定的数控加工中心结构实现运动学求解,并最终转换为机床可执行的NC代码[2]。狭义的后置处理就是指后置处理算法,即将刀位源文件的数据转换为数控加工程序数据的计算规则。由此可见,后置处理器综合了刀位数据算法处理、机床运动学模型计算求解和数控系统多个模块,决定了数控程序的可靠性。
目前,专业化的建模编程软件丰富,如德国SIEMENS公司的NX软件、美国CNC Software 公司的MasterCAM软件,以及中国北京数码大方公司的CAXA软件,都具有良好的通用性,可以较方便地获得数控程序的刀位源文件。但是,除了随编程软件绑定的后置处理器外,提供专用后置处理器的厂家较少,尤其是在根据实际生产需要改装数控机床后,缺少专用且可靠的后置处理器,得到的NC代码可靠性也较低。因此,搭建满足生产需要的特定后置处理器尤为重要。后置处理器以机床运动模型的搭建及数据换算为数控机床运动控制基础,下面做具体阐述。
2 数控加工中心运动学模型的构建与求解
数控加工中心的后置处理算法是根据机床结构搭建运动学模型,运用坐标变换理论实现刀位点与工件坐标系之间的几何关系转换,并根据该关系式将刀位文件中的刀具矢量转换成加工时机床各轴运动矢量。通过计算推导出的后置处理算法[3],使刀位文件中的加工信息数据转换成数控系统的程序代码。其中后置处理的作用是将通用的前置处理生成的加工轨迹文件转换成特定数控机床识别的数控加工程序NC代码[4]。
在数控加工过程中,我们视工件为静止,刀具相对运动。五轴数控机床是在三轴的基础上加入两个回转轴,刀位点坐标及刀轴矢量作为表达刀具空间位置的重要参数。以实际编程中刀具的变化说明,如图3所示。可见在该曲面区域加工过程中刀位点与刀轴矢量因加工位置的不同有所区别。将刀位点和刀轴矢量分别作为独立变量,选取图中所示3个特殊位置,找出转换关系式并建立数学模型。

图3 数控加工中刀具运动变换示意图
特殊地,刀具由状态1运动至状态2,刀位点空间坐标变换:(X1,YI,Z1)→(X2,Y2,Z2);将两坐标点同置于任意坐标系下(编程坐标系),两者存在线性对应关系,坐标变换数学表达式为:

式中:a1、a2、a3、b1、b2、b3为待定系数;ΔXl、ΔYl、ΔZl为平动变换系数。可见,刀具的运动变换可以用一个空间位置坐标即3个单位矢量的组合构成一个3×4阶矩阵表示,为方便矩阵形式表达,引入比例因子w(设为1,方便计算),这样该线性变换的矩阵表达式如下:
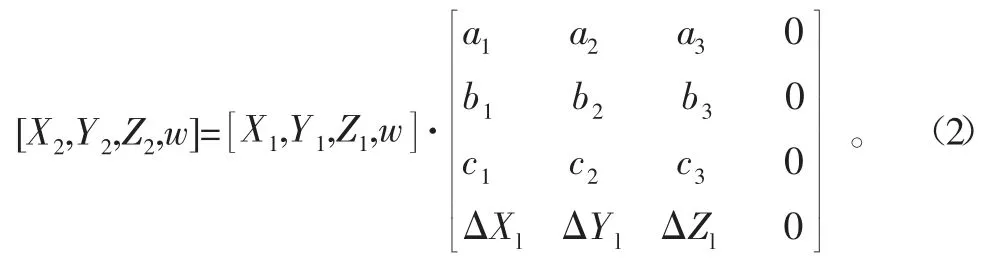
由五轴数控加工中心的结构不难理解,变换矩阵是刀具运动过程中包含平移变换和两个旋转变换(C-A(X)型五轴数控加工中心是A、C两旋转轴)的合成,首先讨论平移变换。
2.1 平移变换

图4 刀位点平动变换原理图
所谓的平动是刀具在运动过程中没有刀轴空间矢量的变化,只有刀位点的改变。如图4所示,在刀具平动过程中刀位点随刀具的运动由初始位置1变到终了位置2,为计算方便,以起始点1为原点建立空间坐标系,则点2可以投影到X-Y平面得到点2′,转变成平面基向量表达。根据公式(1),在XOY平面内内,点1与点2′的关系式可由下式表达:

转换成带有变换矩阵T的表达式:

根据矩阵与转置矩阵的关系,式(4)可改写为:


以上就是刀具在平动方式下X、Y、Z三个轴各自的变换矩阵。
2.2 转动变换
五轴数控加工中心可以实现绕轴旋转功能,这里分别用θa和θc表示绕A轴与C轴的转角。转动后,如果只引进转角,机床的X、Y、Z坐标值不相应加入变化补偿量会产生误差,导致加工执行轨迹与编程理想轨迹不一致,加工过程中会出现过切甚至撞刀情况。因此,多轴数控加工中心的后置处理算法的主要功能是换算出旋转变换引起的刀位点X、Y、Z 坐标值的改变,并引入补偿,实现绕轴旋转前后刀位点相对于工件保持不变,保证加工精度。下面以绕C轴旋转为例说明转动后的坐标补偿算法,如图5所示。

图5 转动变换矢量关系原理图

由平面几何矢量关系建立方程:

同理:

联立式(6)~式(10)得:

转化为矩阵表达如下:
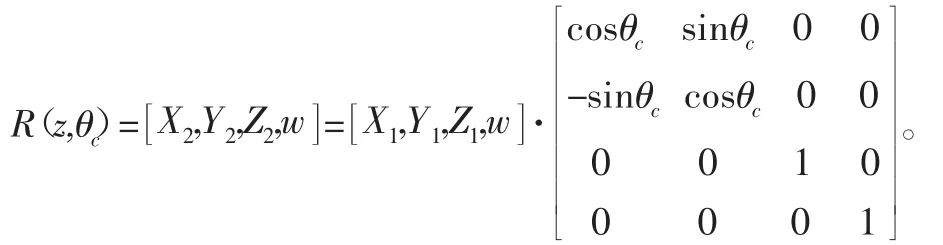
由此得出绕C轴旋转的转动变换矩阵为

同理可知,绕A轴旋转的转动变换矩阵为
3 建立A/C轴旋转角度与X/Y/Z轴向坐标数据补偿关系式
C-A(X)型五轴数控加工中心回转头结构如图6所示。认为A轴与C轴相交于一点,该点为摆动中心Om。摆动中心与五轴机床主轴端面的距离是摆长H,摆动中心到刀位点的距离是L,存在关系式:L=H+d。

图6 C-A(X)型五轴数控加工中心
在前面的推导中得知与工作台顺序连接的高序体的平动变换与转动变换矩阵分别是TX′、TY′、TZ′和R(z,θc)、R(z,θa)。控制刀具位置和姿态的重要参数是刀位点和刀轴矢量,并分别用γ(γx,γy,γz)和τ(τx,τy,τz)表示,其中平动变换坐标系原点的位置可看作任意位置,而转动变换坐标系原点设在转动轴线上,且刀轴初始方向与Z轴平行,故初始状态时,刀位点及刀位矢量在刀具坐标系中的齐次坐标可分别用[0 0 0 1]T和[0 0 1 0]T表达。刀轴矢量刀位点与回转轴焦点距离设为L,这样在以工作台为基准的数控加工中心运动模型中,刀位点到相邻低序体坐标系的静止变换矩阵表示为
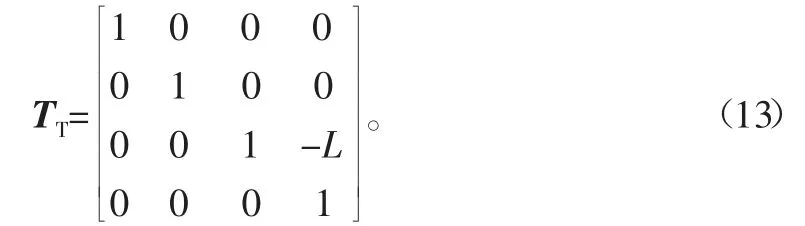
高序转动体子坐标系原点在低序转动体子坐标系中的位置变换矩阵为

参照C-A(X)五轴数控机床的几何多体拓扑结构(如图7)及相应的坐标转换关系式[5]:
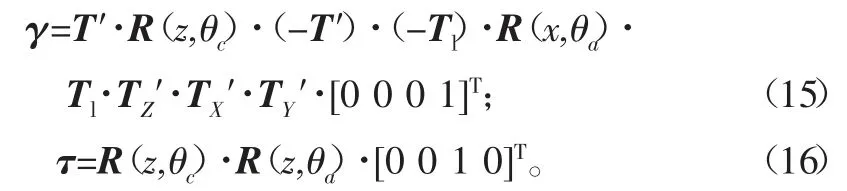
代入已知数据推导:
γx=(yw+yl)·sinθ·c(cosθa-1 )+zw·sinθ·asinθc+xw·z·lsinθ·asinθc;
γy= (yw+yl)·cosθc·(cosθa-1 )+zw·sinθ·asinθc+z·lsinθ·acosθc;
γz=-sinθ·a(yw+yl)+z·l(cosθa-1 )+zw·cosθa;
τx=sinθa·sinθc(X值的变动与转动轴A、C转角有关);
τy=sinθa·cosθc(Y值的变动与转动轴A、C转角有关);
τz=cosθa(Z值的变动只与转动轴A转角有关)。

图7 C-A(X)型五轴机床多体拓扑结构
综上,最终得到五轴联动条件下A/C轴的转角在X/Y/Z三轴的线性坐标补偿表达式,实现控制刀具位置和姿态的重要参数方程,完成五轴机床的运动学求解。采用统一表达式,提高转动连续性。
4 结 语
1)给出数控加工中刀具分别做平动及转动下的刀位点坐标转换关系式;2)建立C-A(X)型双摆头五轴数控机床的多体拓扑结构;3)计算出五轴机床联动时A/C轴旋转角度与X/Y/Z轴向坐标数据补偿关系式,并完成机床运动学求解。
