环境规制与企业全要素生产率能实现双赢吗?——基于两控区政策的实证研究

(中国地质大学(武汉) 经济管理学院,湖北 武汉 430074)

随着环境问题日益恶化,世界各国政府开始重视环境规制。我国在现代化的过程中,虽然取得了GDP迅猛增长的巨大成就,但同时也为高能耗、高排放的粗放型增长方式付出了惨痛代价,严重影响了我国经济的可持续增长和社会的和谐稳定发展。为推动我国生态文明建设迈上新台阶,国家提出了“绿水青山就是金山银山”的新发展理念。但环境保护产业调整必然导致企业环保投资成本增加、技术效率相对迟缓,环境规制和企业生产率之间能实现“双赢”有待深入考证。

除了本地环境规制强度外,区域互动性也可能对本地企业生产率造成影响。在政绩考核体制和治理结构的双重作用下,地方政府为经济增长而展开竞争,环境规制可能存在向上或逐底竞赛现象。那么,由于地方政府环境规制互动形式的影响,企业会在迁址和创新之间做何抉择，从而如何影响本地企业生产率增长？此外,我国地域辽阔,各区域发展不平衡,在基础设施、经济水平、资源禀赋、环境污染等方面存在显著差异。1998年我国提出酸雨控制区和二氧化硫污染控制区,即“两控区"划分方案,两控区和非两控区环境规制力度、经济发展水平相差较大。如在绿色GDP十年研究中发现,如果按绿色GDP核算方法扣除,位于两控区的河北省GDP几乎是零增长甚至是负增长,而位于非两控区的海南省环境污染损失最少,占GDP的比例也很少[1]。那么，我国两控区环境规制政策是在提高环境质量的同时促进企业技术创新、刺激生产率增长,还是以降低经济增长和企业生产率为代价来换取环境改善呢？基于此,本文拟将地理空间的环境规制数据和企业层面的微观数据相结合,通过构建模型,探讨本地与邻近环境规制强度与企业生产率的关系,具体对两控区与非两控区进行对比分析,进一步讨论产权异质性。

1 文献综述

在理论研究方面,对环境规制与企业生产率之间的关系存在两种不同的观点[2]。

一是环境规制有利于企业生产率提高。Porter认为，环境规制和企业生产率之间具备实现“双赢"格局的现实可能性,合理的环境规制能刺激被管制企业在变动约束条件下,优化资源配置效率和改进技术水平,刺激出企业的“创新补偿"效应,从而在部分抵消企业“遵循成本"的同时,提高生产率和国际竞争力[3,4];Berman、Bui通过对空气质量环境规制研究发现,环境规制强度较大的地区企业全要素生产率反而有大幅提高[5];徐保昌等研究发现，我国排污征收费用和企业生产率呈“U"型关系,跨越门槛后才可促进企业生产率提升[6];吴明琴选择“两控区"政策下1992—2009年我国280个城市进行研究,发现相比非两控区,两控区的人均GDP增加了8.3%,环境保护与经济增长呈“双赢”局面[7];王俊、蔡濛萌、王佳等研究发现不管是贸易开放带来的环境规制技术溢出还是R&D投入获得的内生性绿色技术进步,都会带动不同污染程度行业企业的生产率提升[8-10];张成等研究表明，环境规制对企业生产率具有促进作用,且长期效果明显好于短期,说明创新补偿效应需要一定的时间过程[11]。

一是环境规制会阻碍企业生产率提高。“制约假说"认为，大多数企业已根据自身技术、资源、市场需求等方面做出最优选择,环境规制必然导致企业成本增加,短期内运用于生产经营的资金减少,会导致企业生产率下降[12]。“污染天堂假设"认为，当一个地区的生产成本因环境规制增加时,追求利润最大化的企业倾向于将企业转移到环境规制较轻区域,而这些区域成为污染密集型企业的“避难所"[13]。Simoes、Marques运用2001—2008年葡萄牙非平衡面板数据分析了5年环境规制对城市废弃物处理行业的全要素生产率影响,发现尽管由于规制透明提高了服务质量,但是城市废弃物处理行业全要素生产率却呈下降趋势[14];盛丹等研究发现，由于两控区严格的环境规制,生产成本大幅增加,两控区依然处在阻碍企业生产率增长的地位[15];孙文远研究得出，我国实施的“两控区"政策总体上不利于城市就业水平提高,导致城市人才流失严重,影响企业创新能力[16]。此外,金刚等研究发现因环境规制区域差异和逐底竞争现象,使污染密集型企业空间自选择效应较大,往往选择迁移至环境规制强度小的区域,导致环境规制区域互动和城市企业生产率形成以邻为壑的关系[17]。

综上所述,众多文献从不同的地区、行业和企业创新等角度出发剖析了环境规制与企业生产率关系。一是欧美等发达国家的环境规制严厉程度远超我国,即使是采用相同的行业数据,两者之间没有可比性。二是我国研究时间大多较为久远,一方面考虑到企业创新补偿需要一定的时间,另一方面随着我国环境规制政策不断修订与完善,可能存在理论研究与当前现实不符的情况。三是较少考虑区域互动性,未对其细分为本地环境规制和邻近环境进行同时研究,且大多数仅片面判断为促进或抑制关系。四是探讨“两控区"政策对企业生产率有何直接影响的文献相对较少,大多数是研究经济增长质量、污染治理绩效、就业情况等。

鉴于此,本文从区域环境规制视角出发,深入研究了本地、邻近环境规制强度对企业生产率的影响。首先,全样本检验我国本地、邻近环境规制与企业生产率之间呈何种关系;其次，将样本划分为两控区、非两控区,具体探讨了“两控区"政策下环境规制与企业生产率有何不同,并对产权异质性做了分析，以进一步厘清两者之间的关系。

2 理论分析与研究假设

实现环境规制和企业竞争、经济增长之间“双赢"的关键在于“创新补偿"效应的大小,准确地说,很大程度上取决于环境规制能否促进企业的生产技术进步。环境规制既有负面效应,也有正面效应。正如颉茂华所言,在生产管理投入一定的情况下,治理污染投入增加挤占了企业其他正常研发投入,必然导致企业生产率降低,这时本地环境规制与企业生产率、经营绩效呈负相关[18]。随着本地政府不断加强环境规制力度,当达到一个“极点"以后,被动接受环境规制不寻求生产创新的企业需要支付更高昂的环境规制成本,最终只能被淘汰,存留下来的富有市场竞争力的优势企业更重视技术创新。随着时间的推移,在治污技术创新边际绩效递减规律的作用下,企业更倾向于技术创新,通过提高企业的生产率水平或治污能力,最终减缓或抵消政府环境规制给企业增加的环境成本,称为环境规制的“创新补偿效应"。尽管在某些情况下生产中的污染排放可能会有所增多,但由于生产工艺的改进,提高了企业收益,可支付污染处理成本。正是在这种较强的环境规制下,企业生产率反而得到了较快提升。基于以上分析,提出假设1——本地环境规制强度与企业生产率呈“U"型关系。

考虑到各城市区域互动性既存在竞相向上,又存在逐底竞赛现象,邻近城市环境规制强度会对本地企业生产率产生显著影响。根据“污染天堂”假设,若地理相邻城市间环境规制强度有所差异,则会引起污染企业的空间自选择效应。随着邻近城市环境规制强度增大,不愿意就地创新的企业为了逃避环境规制成本,往往会选择迁移到环境规制强度较小的地区。此类企业大多数属于当地生产率较小的企业,考虑到相邻城市间整体平均生产率相差不大,会导致接收地的企业整体平均生产率下降,此时出现“以邻为壑"的现象。但随着邻近环境规制强度越来越大,两地环境规制强度相差甚远时,本地政府为了营造绿色良好环境，赢取外来投资者和公众的欢心,也会加强环境规制,邻近城市企业的污染转移天堂不复存在。同时,邻近地区环境规制强度加大,本地企业既无环境规制强度较小的地区转移,又不进行企业创新而遭淘汰。相反,存留下来的富有竞争力的企业倾向于选择就地创新,从而提高了本地企业生产率水平,此时出现“以邻为伴"的现象。基于以上分析,提出假设2——邻近环境规制强度与企业生产率呈“U"型关系。

我国在1998年批准实施的“两控区"政策,一定程度上缓解了空气污染加重的趋势,那么对企业生产率有何影响呢？从假设1、2可推测:当一个地区实行较为严苛的环境规制政策时,有助于更快跨过门槛,进入“U"型曲线的右半部分,环境规制与企业生产率呈正相关阶段。相比非两控区,两控区严格的环境规制,一方面使两控区内低效率企业淘汰比例更高;另一方面企业“被逼"技术创新,提高了自身生产率,在弥补环境规制成本的同时,反而促进了地区生产率和经济绩效提升,“波特假说"在此得到验证。相反,由于非两控区环境规制管理较宽松,企业往往采取被动治理污染或企业迁址的态度,创新补偿效应较弱,更多的是成本遵循,给企业带来较大的经济压力,“制约假说"和“污染天堂假设"在此得到验证。基于以上分析,提出假设3——两控区较严格的环境规制强度促进了该地区的企业生产率,非两控区则相反。

3 研究设计

3.1 样本选取与数据来源

本文以2014—2017年A股上市公司为研究样本。样本筛选过程包括:①剔除被PT、ST、*ST、S*和S的上市公司;②考虑到西藏地区的特殊性和“三废"数据较难收集,剔除了西藏地区的上市公司;③剔除某些计算指标缺失和异常的样本。经过以上程序,最终获得6152家样本。

本文的数据来源主要包括:①工业产值、工业“三废"数据来自于相关年份的《中国城市统计年鉴》、《中国环境统计年鉴》;②企业全要素生产率数据来自于国泰安数据库;③控制变量主要来自于相关年份的《中城市国统计年鉴》、国泰安数据库和上市公司的年报。

3.2 变量定义与衡量

被解释变量:对企业生产率指标的选择一直是相关研究的难点,也是本文的重点所在。本文参照鲁晓东、胡晓琳和叶康涛的研究，选用全要素生产率(TFP)作为企业生产率指标,分别运用OLS方法和LP方法进行生产率计算[19-21]。全要素生产率通常表示扣除相关要素贡献后的剩余生产率水平,更加贴合实际且具有研究意义。采取OLS方法估计TFP,作为以下方程得到的残差,lnVA=α+βklnk+βllnL+FixedEffects+ε。其中,Fixed Effects为年度、行业固定效应。采用LP方法估计TFP,半参数回归的因变量为lnVA,状态变量为lnK,自由变量为lnL,计算时同样控制了年度、行业固定效应。模型计算中的lnVA是按收入法计算的企业增加值取对数,该增加值为本期折旧摊销额+营业税金及附加+营业利润+支付的职工薪酬+利息净支出计算,并通过该省当年产品出厂价格指数平减。lnK为企业的固定资本存量取对数,该固定资产存量为企业固定资产和无形资产历史成本金额计算,并通过该省当年固定资产投资价格指数平减；lnL是企业的劳动力投入即从业人数取对数；lnM为企业的中间品投入,取对数,中间品投入为总产值(以营业收入代替)与增加值之差,并通过该省当年产品出厂价格指数平减。

解释变量:在目前的统计资料中,关于环境规制(ERS)措施的直接数据较难获取,已有文献采取多种不同的替代指标来衡量环境规制强度。环境规制指标分为不同类型,分别是行政命令型、市场激励型、公众参与型、环境规制总体综合指数[22]。本文采取第四种综合指数方法测量地区环境规制强度。由于环境规制的效果具有滞后性,选择相较于样本前一期的2013—2016年数据计算环境规制强度。

本地环境规制(ERS):借鉴黄志基、唐国平[23,24]关于“工业三废"排放量综合指数的计算方法,构建区域层面的环境规制强度指数ERSit。

计算城市在全国范围内的环境污染排放相对强度POijt:

(1)

式中,POist为第i个城市第t年第s种污染物的环境污染排放相对强度;Mist为第i个城市第t年第s种污染物的排放总量;Nit为第i个城市第t年的实际工业总产值。POist的数值越大,表示第i个城市第t年第j种污染物的排放强度在全国范围内相对越高,环境规制强度越弱。

计算环境污染排放相对强度综合指数POit。由于POijt是一个无量纲变量,因此进行加总平均是有意义的,计算公式为:

(2)

式中,POit为第i个城市第t年的环境污染排放相对强度综合指数。考察的3种污染物分别为：工业SO2、工业废水和工业固体。

计算环境规制强度综合指数:

ERSit=1/POit

(3)

式中,ERSit为第i个城市第t年的环境规制强度综合指数。环境污染排放相对强度POit越小,ERSit越大,表明实行较为严格的环境标准；反之，则实行较为宽松的环境标准。

邻近环境规制(WER):邻近环境规制表示除了研究样本所在城市以外的其他所有城市环境规制强度的加权平均和。本文运用地理距离权重矩阵法进行邻近城市的权重计算,与简单的Queen型0-1邻接矩阵相比,该矩阵假设任何城市均存在环境规制互动行为,只是距离相距较远则互动行为较弱,计算公式为:

(4)

式中,WERit为第t年除城市i之外所有城市环境规制执行程度的加权平均和;Wij为空间权重矩阵中的元素,指两城市i与j之间距离倒数标准化后的值。

控制变量:企业全要素生产率增长与企业自身属性和企业所在城市的区域属性具有密切的关联,因此本文选取以下相关变量加以控制:①企业层面控制变量，包括资产负债率(Lev)、企业全部从业人数(Size)、公司已上市的年龄(Age)、第一股东持股比例(Share1);②城市层面控制变量，包括法律保护水平(Law)、第二产业占GDP比重(Ind)、人均地区生产总值(Agdp),见表1。

表1 变量含义

3.3 模型设计

考虑到环境规制与企业全要素生产率不一定为简单的线性关系,本文将环境规制的一次项和二次项同时引入回归模型中,构建以下模型:

(5)

(6)

式中,TFPint为第i个城市第n个企业第t年的生产率,分为TFPOLS和TFPLP;ERSit-1、WERit-1分别为第i个城市第t-1年的本地环境规制强度、邻近环境规制强度;controls为控制变量,如城市层面和企业层面等;ε为残差项。模型估计采用Stata15.1软件。

4 实证分析及结果

4.1 实证分析

变量的描述性统计:从表2可见,LP方法计算的企业全要素生产率(TFPLP)均值为15.28,标准差为0.804,最小值为12.80,最大值为19.00，两者之间的差异不明显,标准差较小,说明企业生产率的数据较集中,采用OLS法的特征相同。环境规制强度综合指数(ERS)均值为3.798,最小值为0.218,最大值为11.45,最小值与最大值之间差距较大,表明本地环境规制强度存在明显差异,且大多数本地环境规制强度较小。邻近环境规制强度(WER)均值为2.461,标准差为0.691,最小值为0.674,最大值为4.580,说明不同地区的邻近环境规制强度存在明显差异。资产负债率(Lev)平均值为0.410,企业从业人数(Size)均值为6811。公司上市年龄(Age)均值为18.17,第一大股东持股比例(Share1)的均值为35.78%。该省法律保护水平(Law)的均值为9.147,第二产业占GDP比重(Ind)均值为41.43%,人均地区生产总值(Agdp)为74806。

相关性分析与共线性识别:相关分析可对变量之间的相关程度和相关方向进行初步了解,两个变量之间的相关系数绝对值越大,说明两个变量之间的相关性越强。一般情况下,解释变量与控制变量之间的相关系数在0.8以上,说明模型有可能存在严重的多重共线性问题。各变量之间的Pearson相关系数见表3。

表2 变量描述性统计

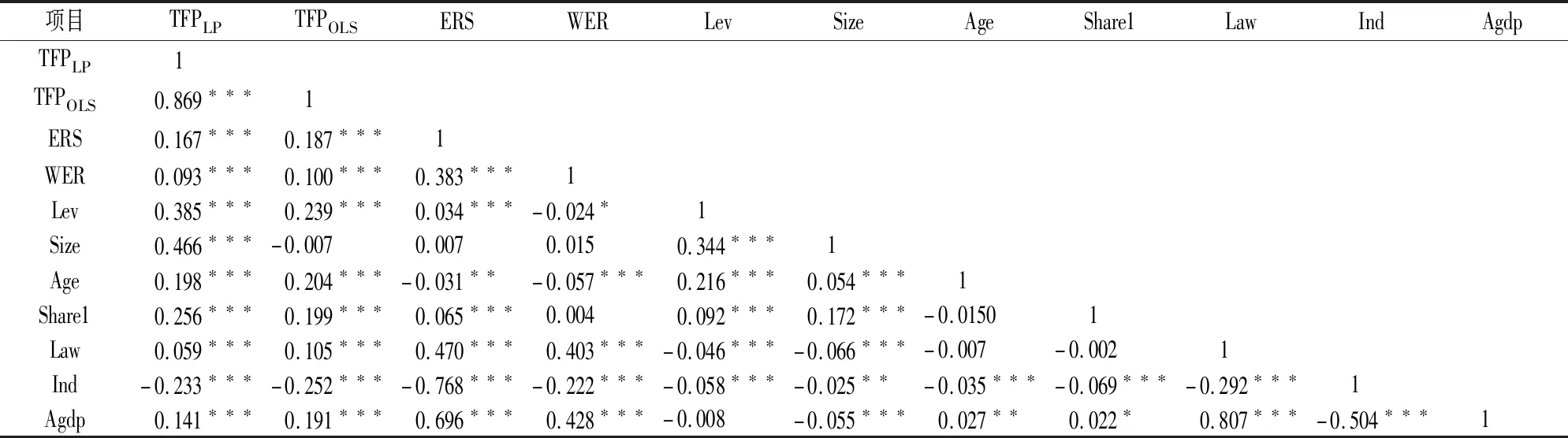
表3 变量的Pearson相关系数检验

注:*、**、***分别表示通过10%、5%和1%的显著性水平检验，表4、5、6同。

从相关系数可见,TFPLP、TFPOLS与ERS的相关系数为0.167、0.187,在1%的显著性水平下呈显著正相关,说明在没有其他因素影响的情况下,本地环境规制强度越强,企业的生产率越高。TFPLP、TFPOLS与WER的相关系数分别为0.093、0.100,在1%的显著性水平下显著正相关,说明在没有其他因素影响的情况下,邻近环境规制强度越强,企业生产率越高。TFP与Lev、Size、Age、Share1、Law、Agdp均呈正相关性,与Ind呈负相关性。相关分析只是对变量间的相关性进行初步分析,并未加入其他变量进行控制,具体分析需要在回归分析中进行验证。此外,大部分解释变量和控制变量之间的相关性都较低(在0.8以下),可推断模型不存在严重的多重共线性问题。为了进一步准确验证模型是否存在严重的多重性共线性问题,本文采用了方差膨胀因子检验,发现各变量的VIF值都较小(小于10),证实了模型确实不存在严重的多重共线性问题。

由表4可知,模型1的全样本ERS回归结果在LP、OLS方法下一次项系数分别为-0.0464、-0.0430,二次项系数分别为0.00476、0.00418,且都在1%的水平上显著,说明本地环境规制强度对本地企业生产率存在“U"型,且结果稳健,验证了假设1。模型2的全样本WER回归结果在LP、OLS方法下一次项系数分别为0.0536、0.0542,且在1%的水平上显著,二次项系数分别为0.0347、0.0288,且在5%的水平上显著,说明邻近环境规制强度对本地企业生产率存在“U"型关系,且结果稳健,验证了假设2。为了进一步考察两控区、非两控区不同环境规制强度对企业全要素生产率有何影响,本文将全样本细分为两控区和非两控区,并带入式(5)和式(6)进行检验。

表4 全样本ERS及WER回归结果

(续表4)

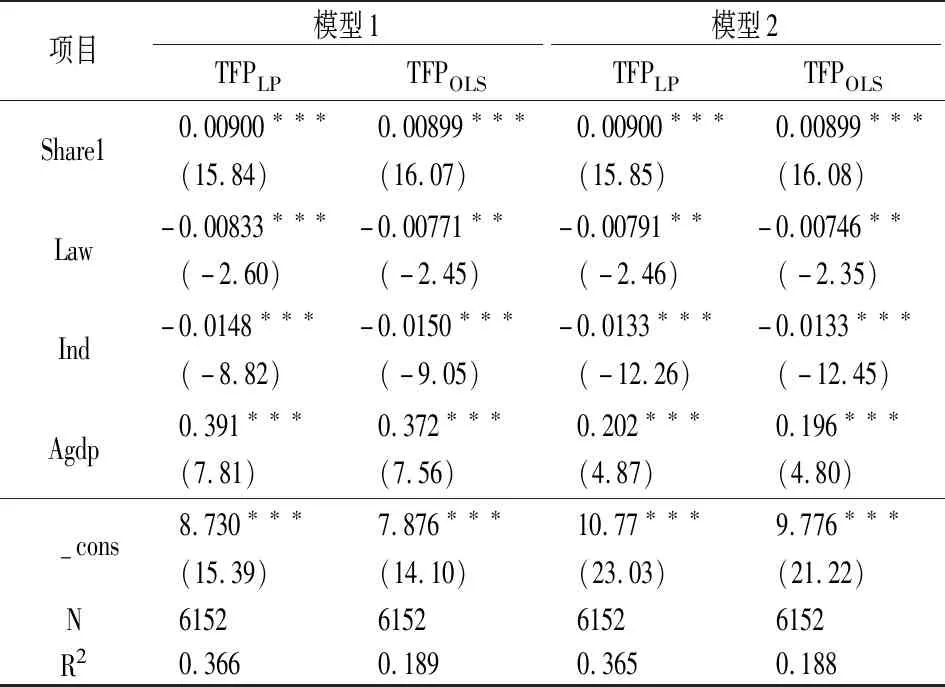
项目 模型1 模型2 TFPLPTFPOLSTFPLPTFPOLSShare1 0.00900∗∗∗ 0.00899∗∗∗ 0.00900∗∗∗ 0.00899∗∗∗ (15.84) (16.07) (15.85) (16.08)Law-0.00833∗∗∗-0.00771∗∗-0.00791∗∗-0.00746∗∗ (-2.60) (-2.45) (-2.46) (-2.35)Ind-0.0148∗∗∗-0.0150∗∗∗-0.0133∗∗∗-0.0133∗∗∗ (-8.82) (-9.05) (-12.26) (-12.45)Agdp 0.391∗∗∗ 0.372∗∗∗ 0.202∗∗∗ 0.196∗∗∗ (7.81) (7.56) (4.87) (4.80) -cons 8.730∗∗∗ 7.876∗∗∗ 10.77∗∗∗ 9.776∗∗∗ (15.39) (14.10) (23.03) (21.22)N 6152 6152 6152 6152R2 0.366 0.189 0.365 0.188

注:回归系数下方括号内为t值,下表同。

由表4可知,模型1的两控区ERS回归结果在LP、OLS方法下一次项系数分别为-0.055、-0.053,二次项系数分别为0.006、0.0058,且在1%的水平上显著,说明两控区本地环境规制强度对本地企业生产率存在“U"型关系,且结果稳健。模型1的非两控区ERS回归结果在LP、OLS方法下的一次项系数分别为-0.0358、-0.0294,且分别在5%、10%的水平上显著,说明非两控区本地环境规制强度与本地企业全要素生产率存在着负相关关系。对于两控区而言,非两控区的环境规制强度较低,处在“U"型关系的左半部分,本地环境规制抑制了企业全要素生产率。因此,我国应加强对非两控区的环境规制力度,以尽快突破拐点,进入“U"型的右半部促进阶段。

由表5知,模型2的两控区WER回归结果在LP、OLS方法下一次项系数分别为0.0842、0.0805,且在1%的水平上显著,说明两控区邻近环境规制强度与本地企业全要素生产率存在正相关关系,且结果稳健。模型2的非两控区WER回归结果在LP、OLS方法下二次项系数分别为0.129、0.132,且在1%的水平上显著,说明非两控区邻近环境规制强度对本地企业生产率存在“U"型,且结果稳健。表明相对非两控区而言,两控区的各个城市邻近环境规制强度大,处于“U"型关系的右半部分,对企业全要素生产率的促进作用显著。同时，说明我国“两控区政策"效果显著,既保障了地区环境质量,又促进了企业全要素生产率。

表5 两控区、非两控区回归结果

4.2 讨论

考虑政策的实施效果会因企业产权性质有所不同,在前文的基础上进行讨论。设国企为1、非国企为0,对模型1、模型2分别加入环境规制二次项与产权性质的交乘项进行回归(表6)。回归结果发现，回归系数显著为正,且通过1%的显著性水平检验，表明在两控区和非两控区中,产权性质差异对环境规制与企业生产率关系有显著的正影响。即与非国有企业比较,国有企业与企业生产率的关系更强。我国国有企业承担着大量的社会责任和政策性负担,为实现全社会福利的最大化,政府常作为国有股权的行使者或国有企业的“保护伞",金融机构乐于向国有企业提供政策性信贷,而非国有企业却面临着严重的信贷歧视。国企相对于非国企具有更雄厚的实力和政策适应性,适应环境规制的能力更强,对企业生产率的促进作用明显大于非国企。

表6 产权性质交乘项回归结果

4.3 稳健性检验

为了验证前面结果的可靠性,本文进行了稳健性检验:①将城市废水、费气污染治理设施当年运行费用之和与工业产值之比作为衡量环境规制强度的指标。②在回归模型中添加其他可能影响企业全要素生产率的变量,如企业层面的产权比率、总资产净利润率,以及城市层面的地区生产总值、普通高等学校数等。③将样本选取1/3,再次进行同样的回归。其稳健性检验结果显示,本文的假设通过检验,说明本文模型的稳健性较好。

5 结论与建议

我国各地区环境规制强度相差较大,且平均值和中位数都较小,倾向于向最小值靠近。本地环境规制、邻近环境规制强度与企业全要素生产率都呈“U"型关系。两控区的邻近环境规制与企业全要素生产率呈正相关关系，非两控区的本地环境规制与企业全要素生产率呈负相关关系,说明两控区更为严格的环境规制促进了企业生产率,非两控区则相反。与非国有企业相比,国有企业对环境规制与生产率的促进作用更显著。

综上所述,环境规制强度与企业全要素生产率呈“U"型关系,而我国企业目前环境规制强度普遍偏低,本文提出以下几方面建议:①政府必须做好引导作用。政府完善相关环境保护法律法规、强化环境规制执行力度是目前解决企业环境与企业生产率的前提和主要驱动力。我国现行环境规制强度整体偏低,政府还应加强各地区的环境规制力度,无论是两控区还是非两控区,都应制定更加严格且适当的法律措施,强化环境监督。此外,政府还应针对产权异质性“对症下药",切忌无的放矢,打击非国有企业环境保护的积极性。②企业创新是第一要素。环境规制与企业生产率的最大问题取决于环境规制对企业发展产生何种作用,只有将外生的环境规制阻碍转化为企业内在的发展动力才是当前和未来切实可行的方法。若企业能以环境规制作为契机,积极主动转向绿色创新,升级技术与设备,不但环境问题将迎刃而解,而且企业的生产效率也将随之提高,甚至有可能引领新一轮的经济增长模式。但是解决环境问题并不能一蹴而就,实现环境保护与企业生产率“双赢”也并非易事,只有在政府环境规制和企业自身创新这两方面的不断努力下,这些问题才能最终得以解决。