基于自适应方法的多无人机编队队形控制

2020-03-02张佳龙闫建国张普

航空学报 2020年1期

张佳龙，闫建国，张普

西北工业大学自动化学院，西安 710129

在实际工程中，多无人机编队具有一定的应用价值[1-2]，备受世界各国的广泛关注，尤其在军事应用中发挥着至关重要的作用。因此，无人机编队控制领域，也日益成为学者们研究的热点和关注的焦点。在无人机近距编队飞行过程中，编队控制是维持正常稳定飞行的关键因素之一[3-4]，无人机编队飞行稳定性受到很多外界因素的干扰，比如，风场、尾涡效应、机载任务、飞控系统以及链路等，这些干扰会严重影响无人机编队飞行的稳定性。尤其，风场的大小和方向会改变编队中任意一架无人机的气动力和气动力矩，进而改变其迎角和侧滑角，使得无人机偏离预设的队形，极易与其他无人机发生碰撞。因此，在风场干扰下风场信息的获取非常重要，这使得无人机编队飞控系统设计面临严峻的挑战。

在无人机近距编队飞行过程中，风场干扰是不可避免的。目前，有很多学者提出抑制或者减小风场扰动的控制方法，使无人机编队能够在风场干扰下稳定飞行。 Blake等[5]建立了一种在风场扰动下的无人机动力学模型，通过设计闭环反馈控制器以抵消风场扰动量，使无人机达到一种动态稳定，这种方法简单但精度不高； Saban等[6]提出了涡旋点阵模型方法，估计风场误差精度高且接近实验结果，但这种方法是基于模型控制系统设计，对模型的精度有很高要求，同时还需已知升力在机翼的分布，因而较难实现；雷旭升和陶冶提出了一种风场扰动自适应控制方法[7]，通过建立矢量场和滑模控制结合起来的复合控制方法，有效地实现了无人机编队在风场干扰情况下按照预期的轨迹飞行；本文作者团队[8-9]利用位置矢量合成对风场实时估计与航迹修正，能够准确估计风场信息，增强无人机的抗风场干扰能力；陈文华等[10]提出了一种基于干扰观测器控制(Disturbance Observer Based Control)方法，广泛应用于外界扰动、参数不确定性以及模型不确定性等领域，取得了显著的成效。在风场估计研究领域中尤为突出，能够有效抑制风场引起的扰动对无人机编队控制的影响。目前，在风场环境下，单机的航迹修正以及双机目标跟踪的相关研究已取得初步进展，但关于多无人机近距编队航迹的研究还鲜有文献研究[11]。针对非线性模型干扰观测器全部的状态量均已知的情形，目前尚未找到相关方法对所设计的干扰观测器进行鲁棒稳定性研究[10]。同时，在无人机编队抗风场扰动控制过程中，已有的控制方法从理论上解决了对扰动的感知和检测，并对扰动进行补偿或者消除，使得无人机编队能够快速达到期望队形并保持稳定飞行。例如，模糊控制[12]、神经网络[13]、经典PID[14]等。这些方法使得系统响应时间长、瞬态性能差。

其中，一些鲁棒控制方法已应用在未知风场扰动情况下的扰动抑制[15-16]和在噪声和模型的不确定性的多机编队飞行控制中[17-19]，取得了一定的抑制风场扰动的效果。由于鲁棒控制器是以闭环系统的鲁棒性作为目标设计所得到的固定控制器，具有较好的鲁棒稳定性，但控制很保守，未能达到预期的控制效果。

针对多无人机近距编队执行跟踪、侦察以及作战任务，通过分布式信息交互模式进行编队控制；将多无人机编队简化为相互连接的拓扑网络，通过对不同节点局部信息进行交互，实现对编队的实时控制。多无人机编队受风场扰动的自适应控制是基于网路拓扑图实现的，因风场扰动使得拓扑图中某一节点偏离预定的位置，通过改变节点状态的位置信息达到期望的队形。风场的准确估计是抑制扰动的关键。目前，对风场的状态估计研究主要是使用一致性理论[20-22],解决了机器人协同定位[23]、多机器人编队控制[24]以及协同航迹规划[25]等问题。然而，这些研究仅针对目标在二维空间或风场分解为二维平面进行研究。

针对风场产生的扰动破坏无人机编队队形，提出了一种三维空间的误差抑制自适应控制方法。在本文中，将“长机-僚机”近距编队所处风场简化为3个方向的标量，分别为横侧向、横向以及垂直方向。编队中任意一架无人机受到三维空间风场的干扰，都会使相邻两架无人机在空间3个方向上产生距离偏差，即相对运动模型产生一个增量，通过对3个方向风场的估计，以抵消所产出距离误差。相对于文献[26]，本文所提出的自适应控制方法在风场环境下，能够实现无人机之间相对运动的精确控制，使横侧向距离误差精度提高15%、横向距离误差提高10%以及垂直方向提高5%。因此，本文所提的自适应控制方法，能够有效实现对编队队形的实时控制。

1 数学模型建立

在惯性坐标系和机体坐标系下，建立“长机-僚机”三维空间运动学模型[27]。在惯性坐标系下，x、y、z箭头分别代表东、北以及垂直纸面向外；在机体坐标系下，x轴方向不变，y轴垂直纸面向内，z轴方向朝北。将惯性坐标系的正视图和机体坐标系的侧视图集于一个坐标系中，如图1所示。图中：le、fe和he分别为僚机相对运动的横侧向、横向以及纵向距离误差；lc、fc和hc分别为长机和僚机之间期望的横侧向、横向以及纵向的距离；VL、VF分别为长机和僚机在惯性坐标系下的速度；χL、χF分别为长机和僚机的方位角。

图1 “长机-僚机”近距编队相对运动示意图Fig.1 Schematic diagram of relative motion of leader-follower closed formation

1.1 无人机运动学模型

多无人机编队在飞行过程中，忽略外界因素的干扰，任意一架单机在三维空间的运动学模型为[28-29]

(1)

1.2 无人机动力学模型

在机体坐标系下，任意一架无人机(包括长机和任意一架僚机)的动力学方程为[29]

(2)

式中：u、v、r分别为无人机速度V在x、y、z轴上的分量;φ为滚转角；Fx、Fy、Fz分别为无人机在空间3个方向的合力；ax、ay、az分别为无人机在3个方向的加速度。

对式(1)时间求导，即

(3)

(4)

式(3)可进一步化简为

(5)

将式(5)代入式(2)，即

(6)

1.3 无人机相对运动模型

在“长机-僚机”模式下的近距编队飞行过程中，假设长机在前，僚机在后，同时长机和僚机之间的相对位置保持不变，按照期望的队形飞行。由图1知，lc、fc和hc的表达式为[27]

(7)

式中：χL为长机的方位角；xL、yL、zL和xF、yF、zF分别为长机和僚机在惯性坐标系下的位置。

对式(7)求导整理，可得长机和僚机之间的相对运动方程为

(8)

1.4 风场环境下的无人机相对运动模型

针对“长机-僚机”编队任意一架飞机，具有以下关系，即

ξ=ψ+β

(9)

式中：ψ为偏航角；β为侧滑角。偏航角ψ通常用于闭环控制器设计；侧滑角β在稳态飞行时，期望值等于零。然而，无人机受到风场扰动时，侧滑角β不等于零。因此，侧滑角β包含由风场扰动产生3个方向的误差，这也是本文设计自适应控制器的依据，即偏航角ψ和侧滑角β复合控制器设计。

在“长机-僚机”近距编队飞行过程中，假设除了风场带来的扰动，不受其他任何扰动，则任意一架无人机的侧滑角β不等于零。根据文献[26]知，风场扰动是长机和僚机的相对位置发生变化的诱因之一，本文将风场扰动分解为空间3个方向的定常扰动wx、wy、wz，他们的方向分别沿机体坐标系x、y、z且相对距离为常数。

基于上述的假设，“长机-僚机”之间的相对运动方程在风场环境下可以进一步重写为

(10)

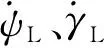
注1本文中，将风场模型解耦为空间3个方向的扰动，由于风场的具体模型作者已在文献[24]深入研究，在此就不做过多赘述。通过解耦的模型(wx,wy,wz)，能够准确对其估计，从而提高自适应控制的精度和编队的稳态特性。

2 自适应控制器设计

2.1 自适应控制方法

自适应控制是一种在风场扰动情况能够保持一致性的有效方法[30]。基于此，本文提出一种多无人机近距编队自适应控制方法用以抵消或者减小风场扰动引起的距离误差，有效保证无人机按照期望的编队飞行。所提出的自适应控制方法，如图2所示。

图2 “长机-僚机”近距编队自适应控制流程图Fig.2 Flowchart of “leader-follower” closed formation adaptive control

注2在文中，被控对象由N-1架无人机和一架虚拟长机组成；虚拟长机携带雷达侦察设备，其余无人机携带作战武器。在集结过程中，所设计的控制器能够使得任意2架无人机之间相对距离误差接近于零，即期望位置和实际位置重合，始终保持相对距离恒定，这样可以保证任意2架无人机避免发生碰撞。

2.2 控制器设计

无人机的运动方程如式(1)所示，它为忽略外界因素的干扰下的模型，加入风场后模型为

(11)

式中：vx、vy、vz为空速在空间3个方向的分量；wx、wy、wz为风场在空间3个方向的分量。风场的加入会影响模型的动力学特性，将风场对模型的扰动，用一组变量为

(12)

式中：Tx、Ty、Tz为无人机外界扰动在空间3个方向的合速度。

将式(12)代入式(11)，即

(13)

假设T*满足：

max(Tx,Ty,Ty)≤T*

(14)

式(14)为外界扰动耦合作用下的极限情形。

(15)

将式(12)代入式(15)，可得

(16)

同时加入风场u输入，即

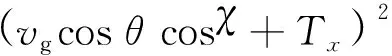
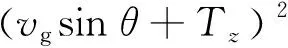
(17)

定义误差为

(18)

为自适应控制器设计做好铺垫，构造

(19)

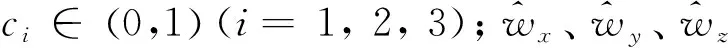
因此，设计以下控制器，即

(20)

考虑无人机编队在风场扰动下队形控制，构建李雅普诺夫函数为

(21)

当t≥0时，易得V≥0。

(22)

对式(22)时间求导，可得

(23)

将式(7)和式(10)代入式(23)，可得

(24)

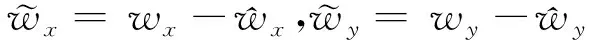
(25)

(26)

于是，式(26)可以改写为

(27)

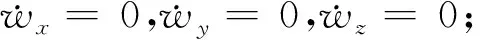
(28)

因此，可得到自适应控制律为

(29)

式中：ki∈(0,1)(i=wx,wy,wz)。如果ki>1(i=wx,wy,wz)，将对其进行归一化处理，确保其为小于1的常数。

2.3 稳定性分析

多无人机编队在风场环境下保持预设的队形飞行，队形稳定控制尤为重要。在2.2节，李雅普诺夫函数已建立，如式(21)所示。

式(22)可进一步化简为

(30)

对式(30)求导，可得

(31)

(32)

式(31)可进一步简化为

(33)

对式(18)时间求导，可得

(34)

将式(18)和式(34)代入式(32)的第2式，可得

(35)

式(35)可进一步简化为

(36)

对式(12)时间求导，可得

(37)

将式(12)和式(37)代入式(36)，可得

(38)

(39)

将式(12)和式(37)代入式(39)，可得

(40)

(41)

无人机编队在正常飞行过程中，有以下关系：

(42)

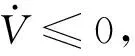
注3本文数据来源于项目的样机，包括质量、体积、气动参数以及相关的飞行参数。得到数据后，在可视化的仿真平台进行“长机-僚机”编队飞行。同时，仿真过程中，每架无人机具有相同运动特性，有助于仿真分析。

3 仿真验证

图3 样机示意图Fig.3 Prototype diagram

其他初始条件如下：CLl=0.118 rad-1,CL0=-0.049，CLα=3.258，CLq=0，CLδe=0.018 9，Γl=2.21，Wuw=0.264，Δα=0.36°，Df=45.65,ΔDf=9.13,Dff=36.52,Lf=1 448.7, ΔLf=43.6,Leff=1 492.3,CDf=0.04, ΔCDf=0.008,CDff=0.032,CLf=1.263 5, ΔCLf=0.038,CLff=1.301 5,ψL0=0 rad/s,xL0=20 m,yL0=20 m,zL0=30 m,xF0=0 m,yF0=0 m,zF0=0 m,le0=0 m,fe0=0 m,he0=50 m,c1=0.2,c2=0.15,kwx=0.009,kwy=0.000 9,kwz=0.001,lc=fc=hc=0 m。

3.1 收敛性分析

(43)

(44)

式(44)进行拉普拉斯变化，即

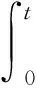
(45)

根据拉普拉斯函数性质，式(45)可进一步化简并整理为

(46)

因此，得出基于拉普拉斯的控制律如式(46)所示。

为了验证所提方法的优点，将所提控制方法与基于拉普拉斯控制方法进行对比。由于长机和僚机之间的相对横向、横侧向以及纵向的距离较近，他们属于近距编队飞行。“长机-僚机”在近距编队飞行过程中存在尾涡效应和风场影响，由于本文仅考虑风场对编队队形的影响。因此，本文在仿真开始阶段忽略尾涡效应。假设编队中任意一架无人机的所受风场扰动的3个方向的初始分量分别为wx=wy=0.6 m/s，wz=0.2 m/s。基于以上的假设和初始条件，仿真结果如图4～图8所示。

图4为“长机-僚机”同时采用拉普拉斯控制方法和所提自适应控制方法在风场中的轨迹图。由图可知，在“长机-僚机”编队飞行模型中，长机在前，僚机在后，且所提控制方法使得无人机编队在风场的环境下更容易收敛到理论值。多无人机编队在风场扰动情况下飞行，将风场3个方向的分矢量逐一准确估计，然后对前行距离误差、横侧向距离误差以及纵向距离误差进行逐一修正，使得编队的队形接近期望的队形。

图5为“长机-僚机”模式下横侧向距离误差收敛曲线。由图可知，无人机编队在风场整个飞行过程中，横侧向距离误差呈现一种先逐渐增大，而后减小直到稳态的趋势。刚开始，长机在前，僚机在后，且长机速度大于僚机，曲线呈现逐渐增大的趋势；在6 s之后，僚机速度逐渐减小，与长机保持28 m/s协同飞行，避免发生碰撞。在稳态状态下，所提自适应控制方法和拉普拉斯方法的横侧向距离误差分别为1.05 m和1.18 m，且所提控制方法误差值始终小于拉普拉斯方法的误差值。

图4 “长机-僚机”运动轨迹Fig.4 “Leader-follower” motion trajectory

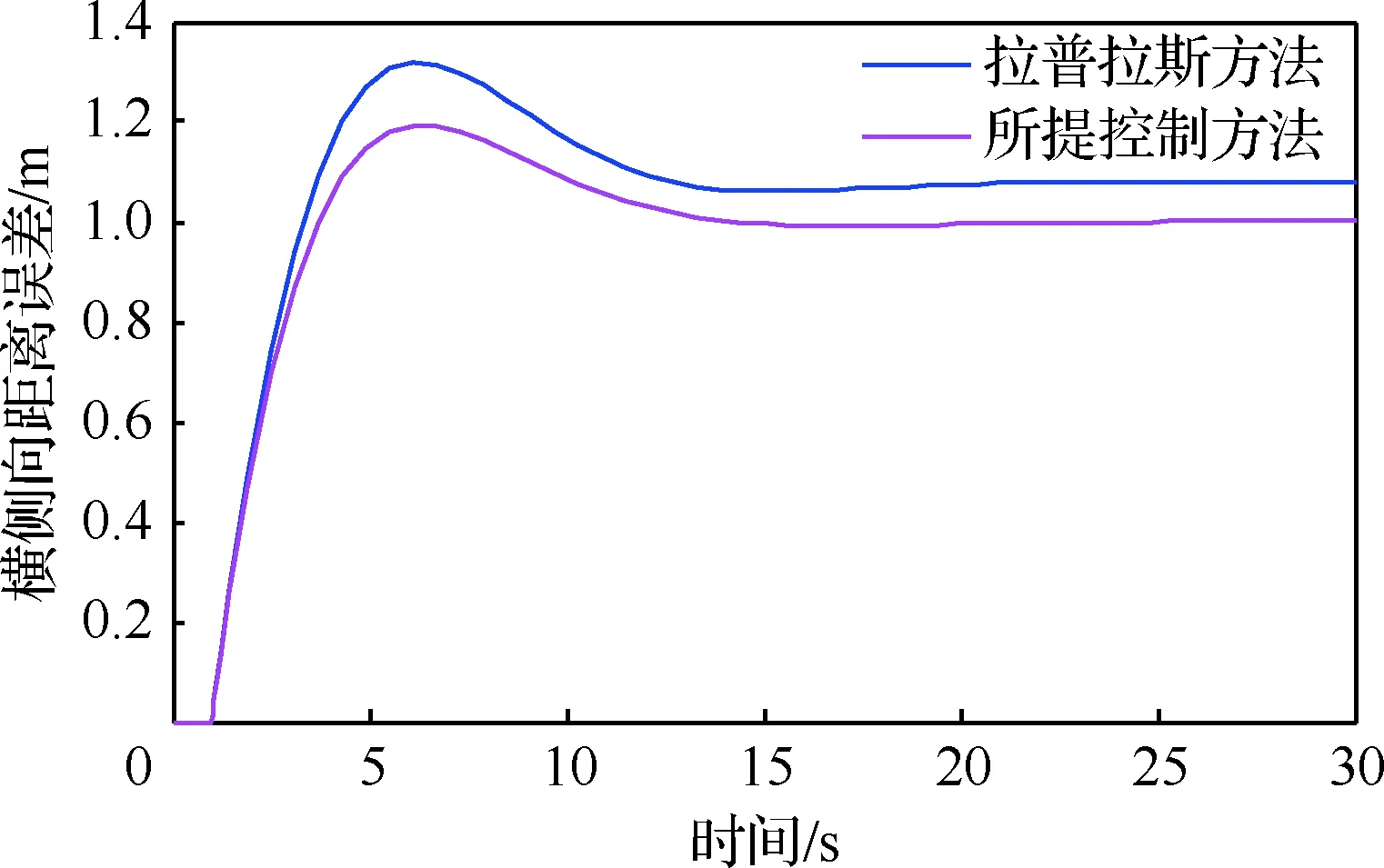
图5 横侧向距离误差收敛曲线Fig.5 Curves of converging lateral distance errors

图6为“长机-僚机”模式下横向(前行方向)距离误差收敛曲线。其距离误差呈现一种逐渐缓慢减小，而后趋于稳态的趋势。刚开始，僚机紧随长机之后，且僚机速度大于长机，他们之间的距离误差缓慢减小；在3 s后，僚机速度减小直至与长机相等，即达到期望的距离。而且，所提控制方法能够使得“长机-僚机”之间的横向距离稍微大些，保证期望队形同时也能够确保避障。

图7为“长机-僚机”模式下相对距离误差收敛曲线。他们之间的相对距离误差呈现一种缓慢减小直至稳态趋势。刚开始，他们之间的相对距离为50 m，随后编队飞行，他们之间的距离逐渐减小直至达到期望的近距编队队形。在无人机编队飞行过程中，风场逐渐被削弱或者被消除，即在消除扰动同时紧密编队飞行。同时，所提控制方法能够使得“长机-僚机”之间的相对距离大于翼展距离前提下，保持紧密编队飞行。

图8为“长机-僚机”偏航角指令曲线。他们的偏航角呈现逐渐增大的趋势。在风场扰动情况下，为了能够抵消3个方向的风场矢量扰动，无人机逐渐增大偏航角以修正航向使得按照既定的队形飞行。同时，所提方法能够在保证“长机-僚机”协同编队飞行。

图6 横向距离误差收敛曲线Fig.6 Curves of converging horizontal distance errors

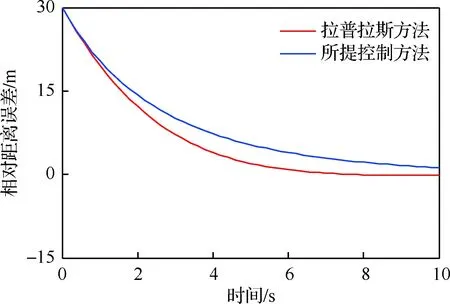
图7 “长机-僚机”相对距离误差收敛曲线Fig.7 Curves of converging relative distance errors of leader-follower

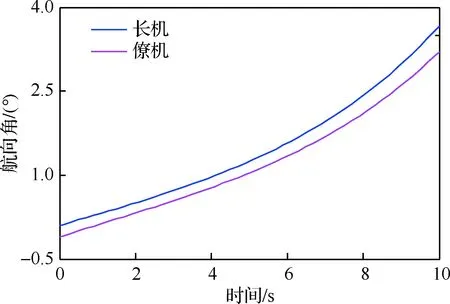
图8 “长机-僚机”偏航角指令曲线Fig.8 Curves of heading angle command of leader-follower

3.2 风场估计

多无人机编队在风场中飞行，风场估计的准确性直接影响编队的队形。在本节中，使用相同的参数和初始条件，对风场在空间3个方向的分量进行了准确的估计，如图9～图11所示。

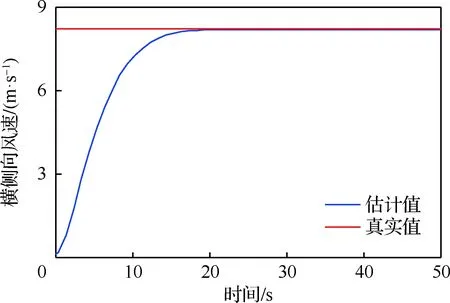
图9 横侧向风场扰动估计曲线Fig.9 Estimation curves of lateral windy field disturbances

图10 横向风场扰动估计Fig.10 Estimation curves of horizontal wind field disturbances

图11 纵向风场扰动估计曲线Fig.11 Estimation curves of longitudinal windy field disturbances

图9为“长机-僚机”模式下横侧向风场扰动估计曲线图。横向风场呈现一种缓慢增大直至稳态趋势。在16 s之前，横侧向风场值增大，使得式(5)等号右侧值增大，引起横向距离误差增大，所提控制方法使得无人机的反扰动能力增强以满足期望队形，即偏航角增大，如图7所示；在16 s后，风场的横侧向估计值逐渐接近真实值82 m/s，使得横侧向距离误差收敛于零。

图10为“长机-僚机”模式下横向风场扰动估计曲线图。横向风场呈现一种先缓慢增大后减小，直至稳态的趋势。在10 s之前，在“长机-僚机”编队模式下，僚机在长机之后且僚机速度大于长机的速度，他们之间的相对距离误差增大，曲线呈现先增大趋势；在10 s之后，其相对距离逐渐缩小，即横向距离误差减小，直至16 s之后收敛于零。既保持期望队形，又避免发生碰撞。

图11为“长机-僚机”模式下纵向风场扰动估计曲线图。纵向风场呈现一种先缓慢增大后趋于稳态，同时对无人机纵向产生距离误差，使得编队队形在三维空间发生改变。在9 s之前，纵向风场扰动不但会使得飞机表面气流分布产生影响，进而影响无人机的升力，而且队形也会受到影响；在9 s后，他们之间的相对距离误差逐渐缩小，直至收敛于零。

3.3 鲁棒性分析

为了进一步验证所提出自适应控制方法的鲁棒性，本节采用相同参数进行仿真研究。由于纵向风场对俯视平面的队形影响甚微，仅对横向和横侧向风速产生的相对距离误差进行对比，如图12和图13所示。

图12为“长机-僚机”在不同恒定风场扰动横侧向距离误差收敛图。可知，在4种恒定风场中，即w=1.8， 2.4， 3.0， 3.8 m/s，“长机-僚机”横侧向距离误差呈现一种先震颤后趋于稳态。“长机-僚机”编队在4种恒定风场中飞行，在10 s后横向距离误差均收敛于零且风场w=1.8 m/s的横向误差最小，即风场越小对队形的影响就很小。同时，所提控制方法均能使无人机在不同的风场情况下达到稳定的稳态，并具有良好的鲁棒稳定性。

图12 “长机-僚机”横侧向距离误差收敛图Fig.12 Convergence diagram of lateral distance errors in a “leader-follower” arrangement

图13 横侧向风场扰动距离误差收敛Fig.13 Convergence diagram of horizontal distance errors under windy field

图13为“长机-僚机”在不同恒定风场扰动横向距离误差收敛图。由图可知，4种恒定风场w=1.8, 2.4, 3.0, 3.8 m/s，呈现一种先缓慢增大后趋于稳定状态，直至接近真实值。在4种风场中，w=1.8 m/s的收敛时间t=6.5 s是最短的，这与图12的分析是吻合的。

4 讨论

4.1 所提方法可行性分析

为了更进一步验所提出方法的有效性，本节将提出的方法与拉普拉斯方法、滑模控制方法[7, 33-34]以及反步推演方法[35]进行了对比分析，同时将所提方法应用在3架无人机的样机进行了实验。采用相同的初始条件和参数，对无人机编队的横向相对距离和相对距离误差进行了分析，如图14和图15所示。

图14 无人机之间的横向相对距离曲线Fig.14 Horizontal relative distance curves between UAVs

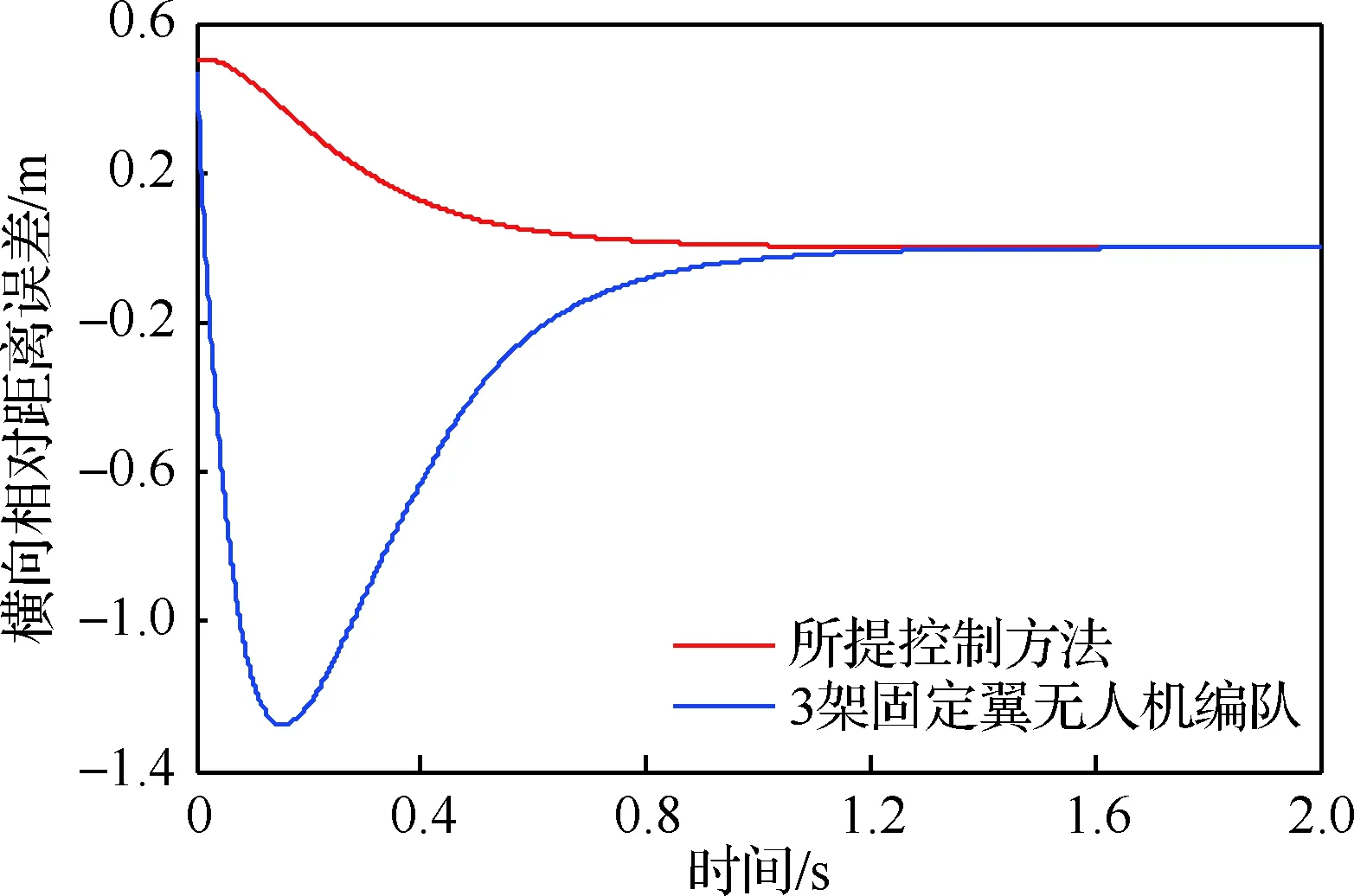
图15 无人机之间的横向相对距离误差曲线Fig.15 Curves of horizontal relative distance errors between UAVs

图14给出了无人机在4种控制方法作用下的横向相对距离曲线图。在实验过程中，将滑模控制方法和反步推演方法直接应用在模型中，采用相同的参数。由图可知，随着时间的变化，无人机之间的横向相对距离大致呈现出一种先快速上升，然后缓慢下降直至达到稳定状态的趋势。与此同时，可将无人机历经的过程分成3个阶段，分别为风场扰动阶段、自适应控制阶段以及稳态阶段。在8 s之前，无人机编队受到风场扰动，编队中的长机和僚机所产生的阻力不同，致使他们之间的相对距离增大，曲线大致呈现快速上升后缓慢下降；在8～13.8 s，无人机编队处于自适应控制阶段，无人机之间的相对距离减小到1 m，曲线呈现出缓慢减小后达到稳定状态；在13.8 s后，无人机编队处于稳定飞行状态，按照既定的队形稳态飞行。在4种方法的控制作用下，无人机编队达到稳态的时间依次为2.2、8、13.5、13.8 s，且滑模控制方法和反步法出现短时间的抖振现象，由此可知所提出的方法动态响应快，稳定性好。

图15给出了无人机之间的横向相对距离误差曲线图。将所提控制方法应用到3架固定翼无人机编队中，对编队中任意2架无人机之间的横向距离误差进行了研究。随着时间的变化，该曲线大致呈现一种先迅速下降后缓慢上升，直至稳定状态。这是由于，无人机在一般风场编队飞行过程中，经历阵风和湍流，该曲线呈现一种缓慢下降后上升趋势；在此之后，无人机之间的相对距离误差在自适应控制下缓慢减小至零，曲线呈现水平状态。因此，所提自适应控制方法能够使无人机编队消除风场干扰，从而稳定飞行。

4.2 一般风场估计和抑制控制分析

在本节，将对3.1节的定常风场估计拓展为一般风场估计，同时对一般风场抑制效果进行了验证，有利于工程实践。同样，使用相同的参数和初始条件，对湍流、阵风以及平均风场进行了估计，并采用本文所提自适应方法对一般风场进行抑制控制，如图16～图19所示。

图16为湍流风场估计曲线图。由图可知，随着时间的变化，无人机所受风场扰动呈现出一种连续抖振后缓慢衰减，直至趋于零的趋势。这是由于无人机编队在飞行过程中，突然遇到湍流风场的干扰，产生抖振，此时启动自适应控制方法，减小或抵消抖振使其缓慢衰减，最终，使无人机编队达到稳定飞行状态。

图17为阵风风场估计的曲线图。由图可知，随着时间变化，该曲线抖振强度呈现一种连续变化的趋势。无人机编队在飞行过程中，遇到阵风风场，则无人机编队队形会被破坏，同时也会使无人机产生连续的抖振。本文所提自适应控制方法，能够及时消除或减弱抖振，使无人机编队及时调整正常的编队稳定飞行。

图16 湍流风场估计曲线Fig.16 Turbulent wind field estimation curve

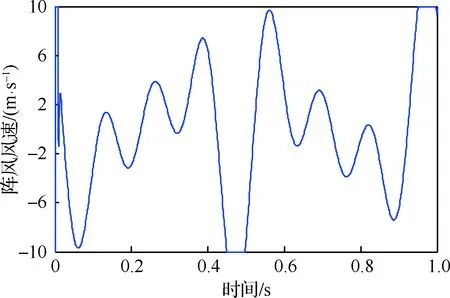
图17 阵风风场估计曲线Fig.17 Gusty wind field estimation curve

图18 平均风速流场估计曲线Fig.18 Average wind speed flow field estimation curve

图19 风场扰动误差曲线Fig.19 Wind field disturbance error curve

图18为平均风速流场估计曲线图。由图可知，随着时间的变化，该曲线呈现一种波动均匀的变化趋势。无人机在飞行过程中，风速的极大值和极小值都会影响无人机编队的飞行稳定性。一般风场的可能会是连续时变的，平均风速估计能够使得地面站工作人员对无人机编队进行实时在线控制。

图19为风场扰动误差曲线图。由图可知，随着时间的变化，该曲线(图16～图18对应的湍流风场、阵风流场以及平均风速流场的误差和)，呈现一种先迅速上升后缓慢下降，直至为零的趋势。刚开始，无人机受到3种类型的风场同时扰动，任意2架无人机之间的相对距离增大，空间3个方向的相对距离误差增大，此时自适应控制及时调整该距离，使其相对距离误差逐渐减小，直至为零。因此，本文所提自适应控制方法能够及时准确消除一般风场所产生的相对距离误差，保证无人机编队按照既定的队形编队飞行。

在本文中，针对定常风场和一般风场进行了估计，同时提出自适应控制方法快速消除一般风场所带来的干扰，能够使得无人机编队按照预期的队形稳定飞行。