基于改进准则法的复合壳阻尼结构拓扑减振动力学优化
2020-03-02袁维东高瞻刘浩康缪国峰
袁维东,高瞻,刘浩康,缪国峰
航空工业南京机电液压工程研究中心 航空机电系统综合航空科技重点实验室,南京 211106
减振作为现代机械发展中一项重要研究课题,如何有效地抑制结构无益振动是研究的首要内容,尤其是在航空航天、智能制造等高动力现代科技的领域,对结构的减振动力学性能提出了更高的要求。其中以“轻”“薄”为主要特性的壳板薄壁构件,在外部激励下极易引起振动,因此势必要对其振动进行控制[1]。对于结构振动的控制一般可分为:主动控制和被动控制。近些年来,在结构表面附加黏弹性阻尼材料的被动减振技术已成为一种实用、有效减振降噪措施。实践表明,黏弹性阻尼材料具有高阻尼特性,在振动变形过程中通过相位的时滞特性来耗散能量,能在十分宽泛的频带内抑制结构的振动与噪声,故常被用作振动结构的减振材料。自从Kerwin和Edward[2]提出以黏弹阻尼材料构建约束阻尼结构以来,其越来越广泛应用于工程实践。不过,对于具有高速和大动力化的减振对象,如航空航天中的多数结构,因其具有轻量化要求,采用在结构上全覆盖阻尼材料的方案,并非是减振控制的最优布局构型。为此,如何有效地敷设黏弹性阻尼材料、提高结构减振效果成为研究阻尼结构拓扑减振的重点。
不少学者研究了壳阻尼结构的减振特性,进一步完善了阻尼结构减振理论和技术。Bieniek和Freudenthal[3]通过建立壳中性面的受迫振动,分析了约束阻尼结构振动;王目凯等[4]提出了在指定频带内能量耗散系数的评价标准,对约束阻尼壳结构进行参数分析。同时,对于薄壁构件在约束阻尼结构最优拓扑构型方面的减振优化,也开展了相关研究工作。Pedersen[5]采用了连续体结构的优化准则法,分析了求解拓扑优化域的局部模态与优化参数的数学逻辑关系;杨德庆和柳拥军[6]提出阻尼胞单元和阻尼拓扑敏度概念,给出了灵敏度排序方式减振优化准则;Lima等[7]推导了复数形式的灵敏度公式,建立了约束阻尼板频率和温变响应的优化减振函数;郭中泽和陈裕泽[8]以模态损耗因子最大化为设计目标,采用变密度拓扑优化,实现了优化准则法求解最优分布构型。可以看出,结构拓扑减振优化的基础理论在不断地建立和推进,但较多的是以薄板的阻尼结构为首选对象给予了研究,而对薄壳减振优化的研究相对较少。Kumar和Singh[9-10]通过实验对圆柱壳主动约束阻尼层位置进行优化。王明旭和陈国平[11]基于均匀化方法,研究了约束阻尼壳结构的拓扑减振效果,得出多模优化效果更佳的结论;柳承峰等[12]以渐进优化算法,研究了约束阻尼壳结构的布局优化,获得较强的振动能量耗损;石慧荣等[13]选取前三阶模态最大损耗因子为目标函数,利用多目标遗传算法对两端简支的圆柱壳进行优化分析;Kim等[14]从模态振型、应变能密度和优化算法3方面,对约束阻尼壳结构减振拓扑构型的振动效果进行了数值仿真和实验验证,进而得出优化算法的拓扑减振优势。对于黏弹性阻尼材料本构数学模型,Johnson和Kienholz[15]基于模态应变能法(Modal Strain Energy, MSE),构建了将阻尼结构复数解简化为实数解模态损耗因子的理论方法。
优化准则法(Optimality Criteria, OC)是拓扑优化变密度法中的一种迭代求解算法,具有完备的理论依据和工程应用价值。其应用于静力学结构时,每一拓扑变量均能取得正数值,然而在动力学结构中则会有非全域迭代拓扑变量的负灵敏度,以至于全域优化变量并不能整体寻优。这种只有其中部分变量参与优化迭代的方式将导致拓扑变量值跳跃和不连续的状况发生,最终迭代结果将不收敛或局部收敛[16-17]。为了满足和提升结构的动力学性能,发挥OC法优势,应用于以航空航天等领域薄壳结构为研究对象的拓扑减振动力学优化问题研究,本文基于变密度法的拓扑动力学优化理论,从数学的理论角度,建立了优化目标灵敏度一般公式,演算全局优化设计变量的改进准则法,并分析了薄壳复合结构的拓扑减振以及多模态减振优化问题。
1 阻尼结构拓扑减振模型
1.1 结构模态损耗因子
为了衡量复合壳约束阻尼结构的减振效果,根据结构振动基本理论,可采用结构模态损耗因子推进阻尼结构拓扑减振动力学优化。对于黏弹性阻尼减振材料,其材料损耗因子比一般弹性材料高几个数量级,通常可忽略金属材料损耗因子,并且在优化迭代中涉及大量的结构动力学参数和阻尼材料复数本构模型的计算,十分耗时,故本文基于能量的角度进行研究。根据有限单元法(Finite Element Method, FEM)和模态应变能法(MSE),可得复合壳阻尼结构的模态应变能计算式为
(1)
式中:Ei、μi分别为第i阶模态应变能和振型;K为刚度矩阵。
黏弹性动力学理论表明,其有明显的温度和频率非线性的变化特性,目前已建立了多种不同的力学本构模型,但较为实用的是常复数模量模型[18],进而复合壳阻尼结构的模态损耗因子写成
(2)
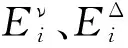
以便于谐响分析,对于复合壳阻尼结构采用黏弹性阻尼材料,基于模态应变能法[19],其模态损耗因子与模态阻尼比之间数学关系:ηi≈2ξi。并可写出阻尼结构的第i阶模态振动平衡方程:
(3)

1.2 插值函数变密度模型
变密度法是基于某种插值模型,建立优化结构材料的物理属性与伪密度之间的函数关系,通过优化设计变量的数值变化来决定优化结构材料的分布状态。固体各向同性材料惩罚模型(Solid Isotropic Microstructures with Penalization,SIMP)的优化求解过程中,阻尼结构的约束材料与对应的阻尼材料存在状态[0,1]作一致变化,可建立复合壳阻尼结构插值模型数学公式为

(4)
式中:E0、ρ0分别为阻尼材料的杨氏弹性模量和密度;n为有限元网格的单元数;χn为第n个单元插值模型的伪密度或设计变量;p、q为SIMP插值模型的惩罚因子;Emin、ρmin为了避免优化迭代中出现奇异值问题,通常设置为0.001;I1(χn)、I2(χn)为材料插值模型函数。
基于有限元法单元矩阵组合理论,可有
(5)
式中:下标s、v、c和上标e分别为约束阻尼结构的基层、阻尼层、约束层和有限单元标识;M为质量矩阵;TN为优化区域约束阻尼有限单元数。
1.3 结构动力学优化模型
任何实际问题均需要构建数学模型,以便于展开问题的定量分析。阻尼结构的拓扑减振优化也不例外,首先建立优化目标函数,明确指明优化求解的迭代方向。在约束阻尼结构中优化目标可以结构振动的固有特性参数,如固有频率、模态损耗因子或模态阻尼比等作为目标,当然也可采用若干特征点的振幅或加速度、动挠度以及响应频率等。鉴于模态损耗因子可以表征在某阶振动时耗损能量多少的度量,其值越大,表示阻尼结构耗能越多,故可以以模态损耗因子为优化目标。然而考虑到优化准则法是以目标函数的极小值形式出现,为了便于借助现存的一些成熟优化迭代技巧推进优化,本文以模态损耗因子负值最小作为优化模型的目标函数。在此基础上,增加移动常数,使目标函数为正值,以便于对目标函数进行数值分析。为满足减振设计的结构轻量化要求,通常优化模型的约束条件之一是对在基体上使用黏弹性阻尼材料的体积作一定限制,与此同时减振优化对象寻优前后,不宜使结构的动态特性如频率、模态、振型等出现过大的变化,影响预期结构优化性能[20-21]。综上因素,复合壳阻尼结构的拓扑减振优化数学模型为
(6)
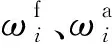
在工程实践中,结构的工作频率段振动通常包括前几阶振型,并且在不同激扰条件下,其振动贡献会发生一定的改变。因此,在考虑多模态复合优化的同时,通过不同的权重系数ϑi来控制各阶模态的减振效果,且最好依据模态参与因子取定ϑi。当然,也可对某一阶频率进行减振优化分析,选取权重系数为1,其他阶次频率权重系数为0,故可看出此拓扑优化目标函数具有较广的适用性。
2 减振优化目标灵敏度分析
变密度法拓扑优化中,优化目标函数的寻优方向主要取决于对拓扑优化设计变量求解的梯度,即灵敏度,它准确反映了优化迭代方向的敏感性。加之目标函数是单模态优化线性叠加的数值关系,由此可先推演单模态减振优化灵敏度数值公式。
对式(2)求模态损耗因子梯度,并整理可有
(7)
(8)
根据结构动力学有限元理论,可知复合壳阻尼结构模态满足:
(9)
将式(9)等号两边同时对χn求偏导,整理得
(10)
(11)
联立式(9)和式(10)整理求解可有
(12)
接着,将式(10)~式(12)变换求解可得
(13)
为了使目标灵敏度具有广泛的应用价值,基于材料插值模型函数,推导一般灵敏度计算公式。
将式(1)对设计变量求偏导,可有
(14)
联立式(7)、式(8)、式(13)和式(14),则整理推导出

(15)
式(4)可作变换有
E′(χn)=I′1(χn)E0=
(16)
ρ′(χn)=I′2(χn)ρ0=
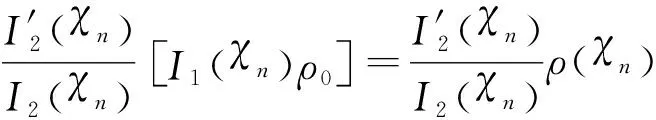
(17)
基于有限元的单元能量理论,可得
(18)
(19)
进一步将式(15)、式(18)和式(19)联立可有
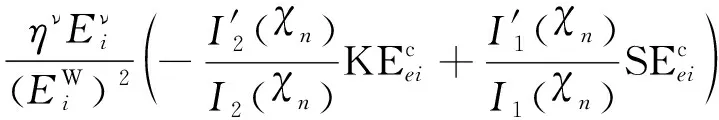
(20)
式中:KEei、SEei分别为当前某一迭代单元的第i阶模态动能和模态应变能;I′1(χn)、I′2(χn)为材料插值模型一阶导数。
3 拓扑减振优化算法
已有研究表明,基于优化准则法(OC)的设计变量启发式迭代格更新方法,是一种与优化结构设计变量数量无关的迭代公式,具有优化寻优效率高和严格的理论推导等特点。不过,在动力学拓扑优化中灵敏度数值以实数范围变化,即正数或负数均可出现。若直接采用静力学中优化准则法进行动力学优化求解,势必引起设计变量负值的出现,将会导致优化迭代无法进行。常规动力学优化准则法通过将正的灵敏度置为零,保留负灵敏度值,而这样做易引起拓扑变量跳跃以及局部优化解[22]。因此,以复合壳阻尼结构为研究对象,基于改进准则法进行拓扑减振动力学演算。
3.1 动力学改进准则法
建立不随优化目标凸性的求解算法,根据优化理论,基于数学规划法中序列凸规划方法构建相似性函数,并建立泰勒展开式逼近,推导优化数学模型严格凸性条件。首先对式(6)演算拉格朗日优化函数[23]:
(21)
式中:Λ、β-n、β+n均为拉格朗日乘子。仅须进一步满足Karush-Kuhn-Tucke条件,并求其极值点处的χn值,即有
∂ψ/∂χn+Λ(∂V/∂χn)-β-n+β+n=0
(22)
为了构造相似性函数,引入移动参数c,令ψ-cV=ψ*,Λ=Λ*-c,并代入式(22),得
(∂ψ*/∂χn)+Λ*(∂V/∂χn)-β-n+β+n=0
(23)
进一步令yn=(1/χn)ζ,根据泰勒展开思想构造逼近函数,即使自变量yn逼近ψ*,接着可令
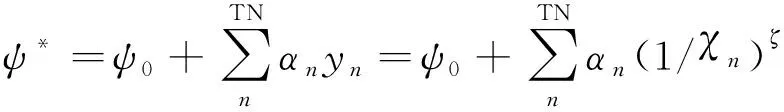
(24)
式中:ψ0为一常数。推导式(24)对yn导数,则
∂ψ*/∂yn=αn
(25)
显然,当αn≥0时,近似函数ψ*具有严格凸性。
另一方面推导式(24)对χn导数,可得
∂ψ*/χn=∂[αn(χn)-ζ]/∂χn=
∂(ψ-cV)/∂χn
化简并整理后,有
αn=-(∂ψ/∂χn-c(∂V/∂χn))(χn)ζ+1/ζ
(26)
c≥(∂ψ/∂χn)/(∂V/∂χn)
(27)
确定移动参数c数值关系,使αn≥0满足函数严格凸性条件。
3.2 构建改进准则法迭代律
在建立凸性条件的基础上,完成启发式迭代格的推导。为此,对式(21)进一步细化设计变量的优化迭代空间,并简化算式可令δn=∂V/∂χn,这样便将式(21)函数整理简化为
式中:
(28)
式中:Ω、-Ω、+Ω分别表示拓扑设计变量的中间值、最小值和最大值集合。为了求解式(28),在求解式(29)所示数学问题同时,结合式(22)和式(23)求得,即
min:ln,χmin≤χn≤χmax
(29)
同理,由拉格朗日极值条件易得
(30)
将αn、δn代入式(30)化简得设计变量满足极值条件迭代格为
(31)
式中:k为迭代次数。若令Q=(∂ψ/∂χn)/(∂V/∂χn),并结合式(27)可知,Q是一个与设计变量数量有关的参量,可建立第k次迭代中参数ck用∞-范数表示:ck=‖Q‖∞,且Q=[Q1,Q2,…,Qn]T。考虑到每次迭代时设计变量的移动极限,故改进准则法的设计变量迭代格为
(32)
并且,
式中:λ(0<λ<1)为设计变量移动极限值。
在优化算法寻优过程中,大量的伪密度设计变量更新带来了优化对象的不同片区物理属性跃变,避免优化前后振型发生紊乱致使优化拓扑构型失效。在迭代优化中通过振型控制因子(MAC)的数值大小[23],直观的反映每次迭代情况,其计算公式为
(33)
式中:τ≤1正系数,一般取值0.9。迭代格更新设计变量时,优化振型趋于稳定的量化MAC近于1。若有变化,则须调整迭代格参数,并作进一步迭代寻优。
复合壳阻尼结构减振寻优,借助大型商用软件ANSYS给予数值处理,通过二次开发语言APDL编程实现改进准则法迭代格。图1为算法程序流程图。

图1 复合壳结构减振拓扑优化实现流程Fig.1 Topology optimization procedure for damping shells
4 优化算例分析
为了进一步分析和验证上述减振拓扑优化的理论,采用航空航天等工程中应用广泛的复合壳结构作为优化对象。
壳结构外形尺寸参数弧度半径R=1 m,转角θ=30°,长度L=0.55 m。基体材料厚度3 mm,杨氏弹性模量43.2 GPa,泊松比0.33,密度1 810 kg/m3。黏弹性阻尼材料杨氏弹性模量15 MPa,密度为1 550 kg/m3,泊松比0.495,材料损耗因子0.75,铺设厚度1 mm。黏弹性阻尼材料应用于被动三层约束阻尼结构,约束层厚度1.5 mm,采用与基层相同的材料。同时作用于结构的谐响应激励力为单位力,提取频率1~200 Hz,图2给出了薄壳一端固支约束、激励点、提取点和前三阶模态应变场。
对结构前三阶模态振型,运用改进准则法进行拓扑减振优化,约束层与阻尼层视为一层优化结构,且优化后材料体积为全覆盖的50%。表1为优化目标函数权重系数的5种不同取值情况,分别代表全覆盖约束阻尼层、一阶优化、二阶优化、三阶优化和前三阶多模态减振优化数值计算的设定值,并列出了相应的结构损耗因子和固有频率的数值结果。其中,主要考虑前三阶模态减振中的权系数加权作用,以求结构损耗因子最大值的优化目标,因此权重系数ϑ1=ϑ2=ϑ3=1/3。以下拓扑减振分析中,未指明的情况下均为改进准则法的寻优数据。
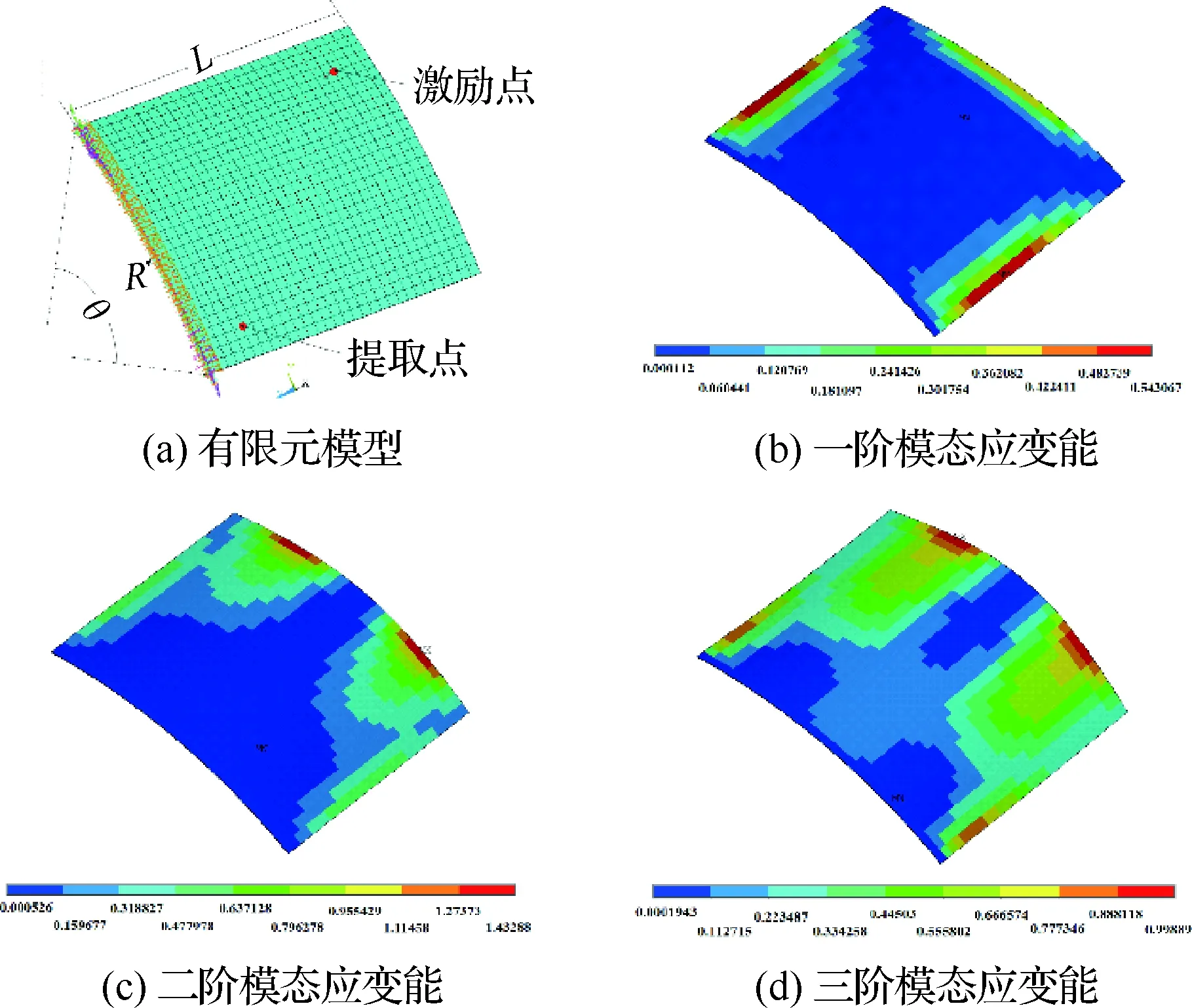
图2 薄壳模型与应变能分布Fig.2 Element model and modal strain energy of constrained damping shells
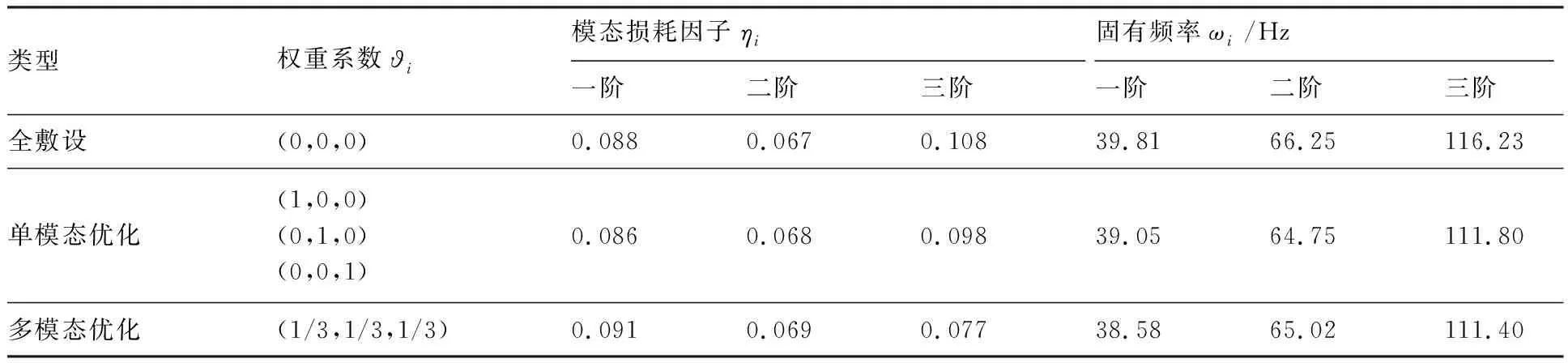
表1 不同权值薄壳结构模态损耗因子和固有频率Table 1 Modal loss factors and natural frequency of single-shell structure
图3(a)、图3(b)与图3(c)给出了针对前三阶单模态优化函数拓扑构型迭代历程。可见在前几次迭代中,拓扑迭代曲线有大幅度的变化,均有先下降再上升的趋势,说明了OC算法极值寻优的基本特性;同时拓扑构型云图中出现了大量的中间密度,并开始显现出优化拓扑构型的初始原貌。随着迭代的进行,设计变量的中间值逐渐变少,向[0,1]两端趋近(深蓝色为0,红色为1),最终优化拓扑构型稳定清晰。它表明从整体上看迭代稳定前波动幅度较大,目标函数的寻优域范围变化大,具有不单一变化于一极点而稳定的特点。进一步与图2中应变能云图对比分析,不难发现各阶拓扑构型迭代过程中,密度值较大的阻尼约束单元优先分布于应变能相对较大的位置,密度值小的处于应变能较小的位置,随着迭代的进行密度较大趋于1,表示敷设阻尼材料位置,密度较小多半趋于0,表示原基体。这主要由于应变能小的位置,黏弹性阻尼材料对振动能耗损相对较弱。从化增加,出现曲线的跌宕,这是由于随着非最大应变处粘贴阻尼材料的进行,最大应变与小应变处交替迭代更新,拓扑结构阻尼约束单元出现了大微量的变化,使得寻优范围扩大,出现了显著的不局限于已有某一迭代极值点的优化过程。
根据振动理论,结构振动通常是由多阶振型相互作用的结果,在工程实际中,常常是固有频率最低的几个振型的贡献占了压倒地位,多模态振动是承力件基本运动状态。图3(d)为多模态优化迭代历程,从图中可看出,伪密度值逐渐迭代至0或1,其数量比重增加,中间密度减少,稳定的减振拓扑构型渐显。同样可看出,高密度阻尼材料主要敷设在前三阶应变能较大的交集区,反之,低密度阻尼材料在最小应变能的交集区。
进一步可看出,薄壳阻尼材料的减振优化迭代次数较少,便于形成灰度值少(产生于中间密度数量少)的拓扑构型,迭代至25次以上可达到寻优稳定状态。不同的权值优化历程图均显示,在第4次迭代左右出现了起伏较大的波动,且优化拓扑构型云图趋向0值增多,这是由于集中于中间密度的趋势减弱,两级趋向性增强。在此基础上,随着迭代次数进一步增加,拓扑构型的灰度渐少,最终优化迭代至稳定的减振拓扑构型。
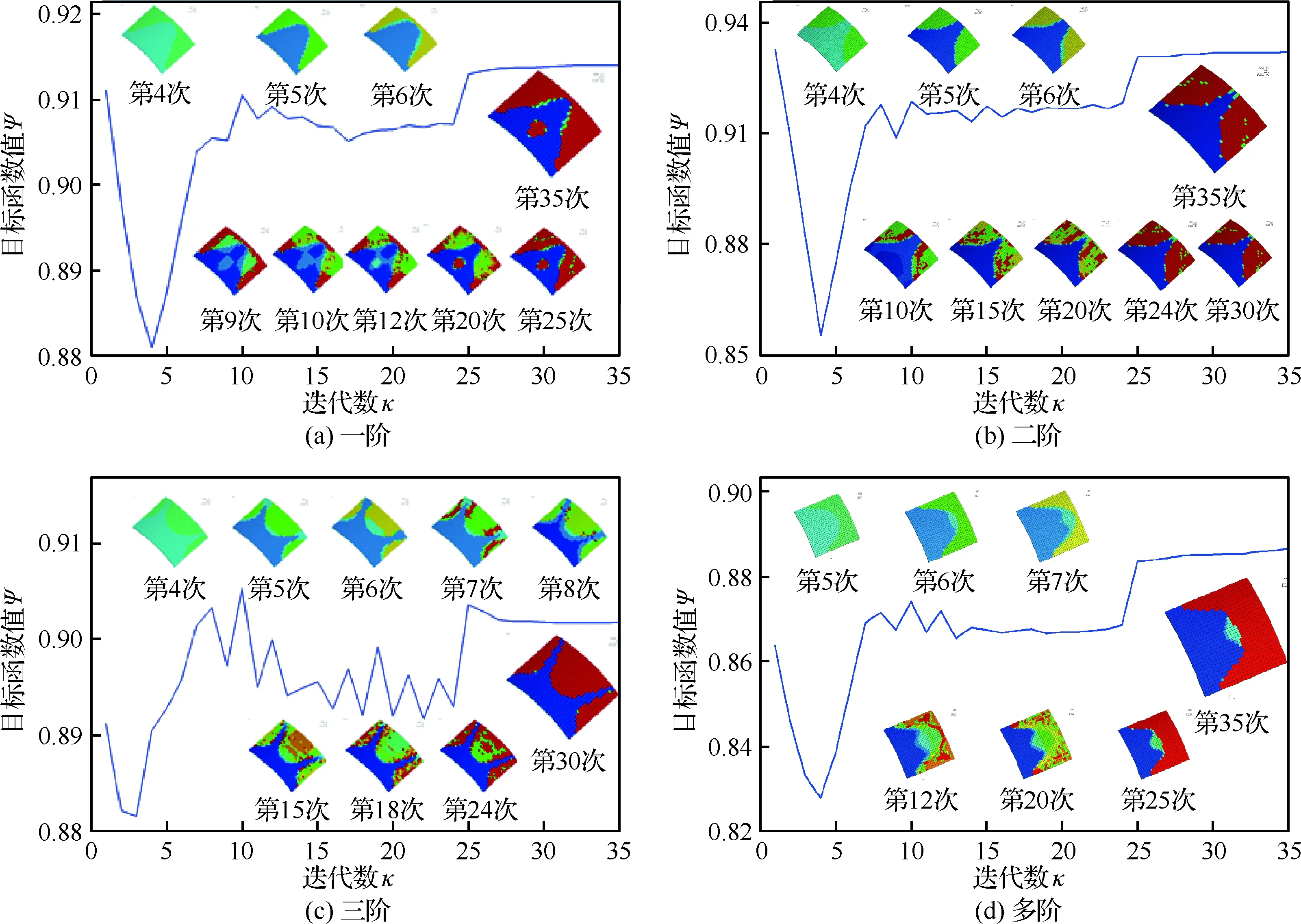
图3 模态优化函数拓扑构型迭代历程Fig.3 Iteration of modal optimization function and topology shape
对于不同权值函数,固有频率优化迭代变化随优化函数波动而改变。图4给出了其变化历程,各优化函数均以较小的波动范围引起固有频率的变化,变化差值在±5 Hz以内,因此模态损耗因子的优化不影响结构固有频率和振型,并且满足优化模型约束条件的给定值,优化稳定后的数值可见表1中给出前三阶模态固有频率。
随着优化函数的迭代,不同阶的模态损耗因子具有相应不同的变化。图5给出了对应于不同阶次优化函数的损耗因子迭代过程。从图中可知损耗因子值初期递增,随后减小逐渐趋于稳定,以及其优化曲线变化与目标函数的数值关系式(6)
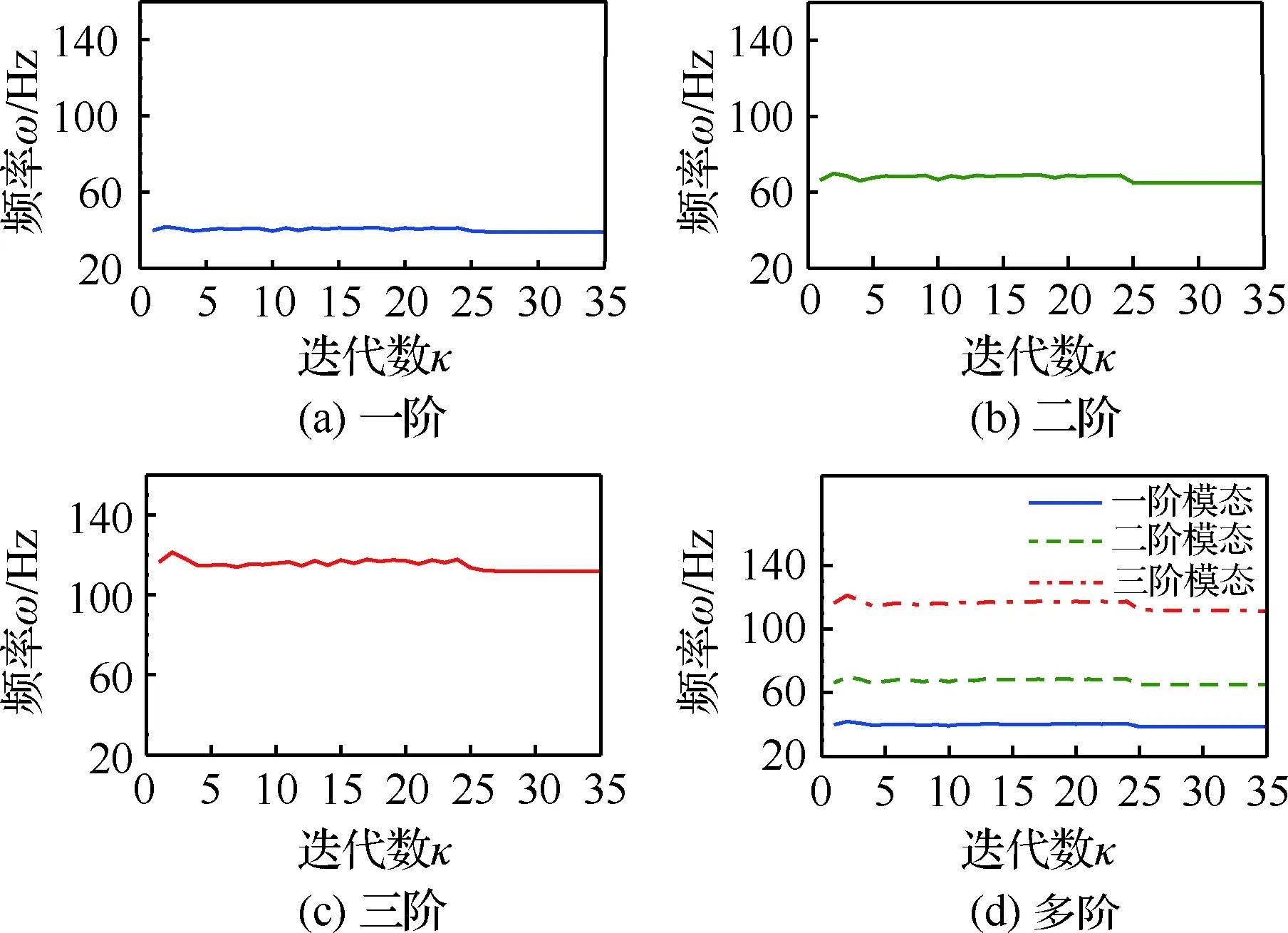
图4 模态优化固有频率迭代历程Fig.4 Iteration of modal optimization natural frequency

图5 模态优化损耗因子迭代历程Fig.5 Iteration of modal optimization loss factor
保持一致。同时可得中间密度较为集中时,模态损耗因子的数值出现随之增加的趋势,相反趋于两级或灰度值减少时,损耗因子呈现下降。这表明在目标函数值趋于稳定时,若灰度较多,虽表现出损耗因子增加或稳定,但由此提取的拓扑构型与计算的损耗因子相比会有所减小,导致结果存在虚增情况。在此,进一步验证了抑制灰度值的重要性。
不难发现,图3~图5中在迭代25次附近曲线出现突变,呈现出上升的趋势,紧接着趋于稳定变化。为了抑制灰度值的产生,并且使趋于1的或趋于0的伪密度分别为设计变量最小值χmin和最大值χmax,因此在算法迭代中可增大插值模型惩罚因子p和q,减小设计变量移动极限值λ,这样可以在优化迭代稳定的后期减少中间密度材料的存在,提高拓扑构型约束阻尼层与实际所采用材料属性的一致性。
图6给出了针对灵敏度的正负数量的迭代跟踪,提出灵敏度正数比=正数/总数,并以此作为度量分析。优化过程中起始迭代次数均以大于0.6的比值寻优,中间迭代数以低于0.6的比值寻优。反映了动力学优化中若仅以灵敏度负值参与迭代优化,难以满足体积约束条件,会使寻优域缩小,表明灵敏度正负比值的波动性,可能引起出现极值点解和拓扑构型跳跃。
为此,采用一般优化准则法对上述算例展开拓扑减振优化。图7(a)、图7(b)和图7(c)为一般法单模态优化迭代历程。与图3对比,可以看出在迭代优化初期,曲线变化比较相似,但从拓扑构型云图上看一般法优化的中间密度数量较多,趋向于密度为0或1的变化减弱。可看出,图7(a)在迭代10次附近、图7(b)在迭代13次附近曲线出现明显的下降,随着中间密度值增多,优化拓扑构型反而出现倒退的现象,并结合图6分析,可得能参与优化迭代的设计变量正数比明显高于体积约束系数0.5,致使中间密度增加,且优化满足不了减振优化模型的体积约束条件而迭代优化中止。
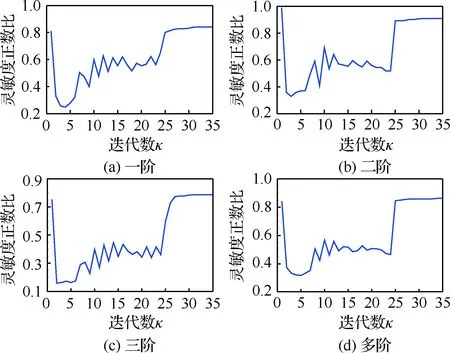
图6 模态优化灵敏度正数比迭代历程Fig.6 Iteration of modal optimization sensitivity positive ratio

图7 一般法模态优化拓扑构型迭代历程Fig.7 Iteration of modal optimization function and topology shape by unimproved OC method
图7(c)进一步表明一般法的参与设计变量正数比低于约束体积系数时,可进行迭代优化,中间密度较多,迭代变化平缓,反映出寻优极值点不易变化;从图6(c)中可得到迭代后期出现不满足约束条件的灵敏度正数比,但是在设计变量移动极限值的作用下,同样能稳定拓扑构型。
图7(d)给出了一般法多模态优化拓扑构型过程。同样反映出与一般法单模态迭代优化中不易满足体积约束条件的分析相一致的情况。
为了进一步验证其算法的优化效果,采用不同权值拓扑构型作谐响应分析,且与全覆盖约束阻尼层谐响应对比。图8(a)、图8(b)和图8(c)为单阶模态优化谐响分析曲线。与全覆盖阻尼激励幅值相比均有所增加,但增加的幅值较小,同时验证了表1中模态损耗因子变化,在体积减少50%的前提下,一阶和三阶模态损耗因子下降2.3%、9.3%以及二阶模损耗因子上升1.5%;图8(d)给出了针对前三阶多模态权值优化谐响分析曲线,另外结合表1中多模态优化特性数值,结果表明与单模态优化相比,有更好的减振效果,一阶损耗因子增加相对而言较多,提升了一阶单模态优化效果。优化阻尼和全覆盖阻尼结构谐响应分析的共峰值激励频率与表1中优化前后固有频率变化相一致,验证了其合理性。不过,可看出未优化的高阶模态减振幅值相对于全覆盖阻尼有所增加,由于高阶振型较复杂,与敷设在优化区域显现较集中的已优化拓扑构型相比,减振效果有所减弱。
从优化前后幅频特性曲线可以看出,第三阶共峰值均相对较小,根据振动理论,可知激励频率与固有频率较接近时其主振型起主导作用,并且图2(a)所示的提取点位置处固有频率主振型幅值较小,进而使未优化阻尼结构同样出现较低的共振响应峰。
在优化体积减少50%的前提下,壳结构均能优化得到与全敷设约束阻尼材料同等的减振效果,甚至在低频段优化效果有相对大的提升,结构的频率和振型保持在约束范围内,提高了结构的轻量化要求,改善结构减振控制中的稳定状态。
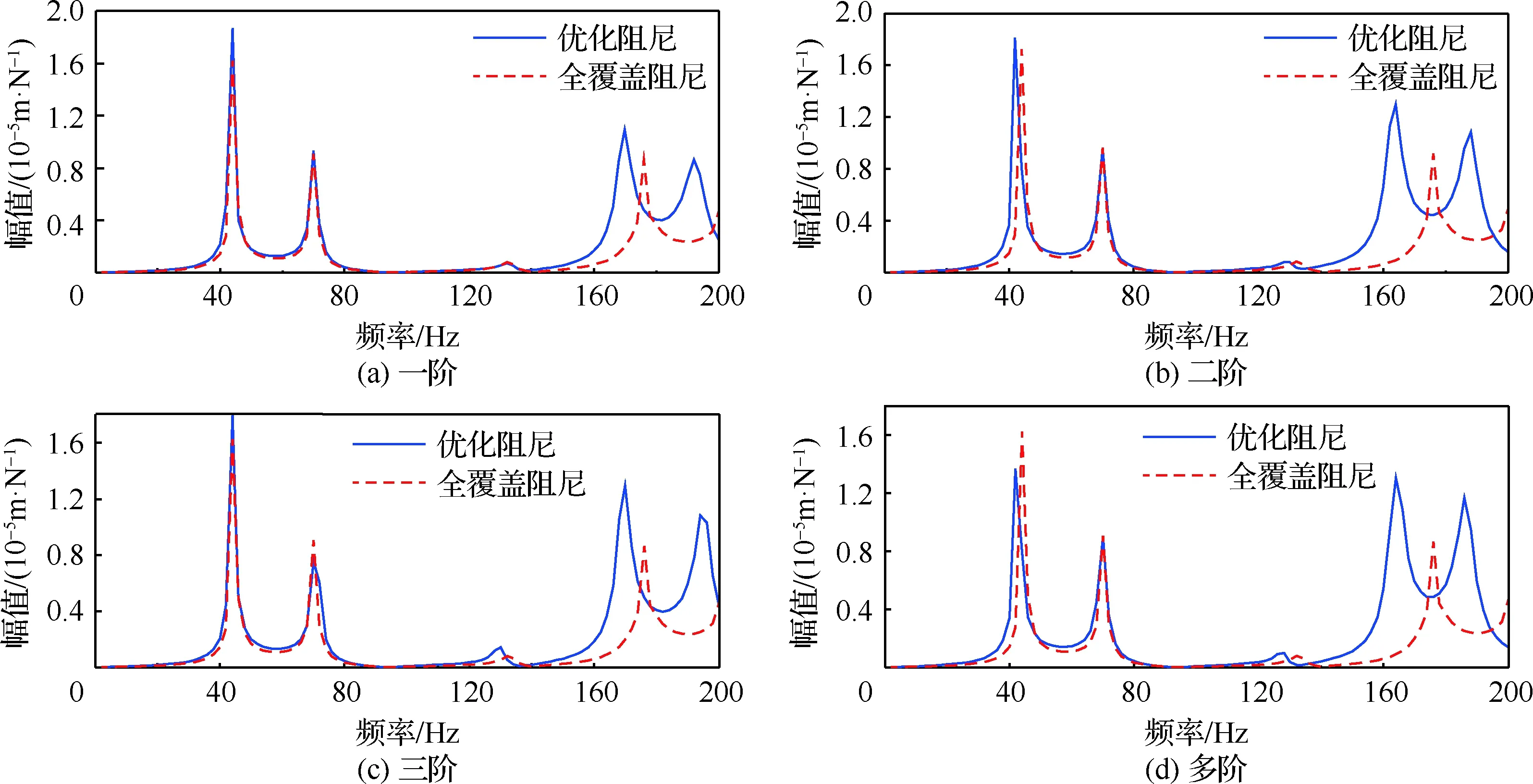
图8 模态优化前后谐响应分析Fig.8 Harmonic response analysis of single shell mode optimiz
5 结 论
1) 以50%为体积约束条件,多阶优于单阶模态优化,得到与全覆盖约束阻尼层相比,模态损耗因子偏差却不超过10%的效果,亦可在合适减少材料的情况下,引起结构损耗因子提高,增加能量耗散,抑制振动响应。
2) 提出对灵敏度正数比的分析,反映出动力学优化中灵敏度正、负数集共存,优化中应避免非灵敏度全域优化迭代发生和拓扑构型跳跃。
3) 拓扑构型灰度越大,模态损耗因子越大,进而在优化过程中,避免因为出现惩罚不够导致稳定构型包含较多中间密度值的情况发生,使得优化结果虚增,同时拓扑构型显示可将约束阻尼材料较多敷设在振动响应大的区域,能够最大限度的抑制振幅。
4) 全域灵敏度改进准则法对复合壳结构不同权值优化,验证了算法具有迭代快、寻优域广和拓扑构型清晰稳定的优势。
