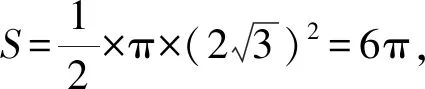立体几何中的“轨迹”问题

王丰萍

以立体图形为载体,以空间想象能力为立意,注重知识的整合与渗透,设置满足一定条件的动点,着力将动点运动的轨迹设计为直线、圆、圆锥曲线或圆锥曲线的一部分进行考查,这是出现在高考或各地模拟考试中立体几何的一类常见问题.这类与“轨迹”有关的问题,在立体几何与解析几何的交会处命题,对促进学生思维能力和掌握核心概念大有裨益,能很好地考查学生的直观想象能力和知识综合运用能力，下面举例来说明.

1 轨迹的判断

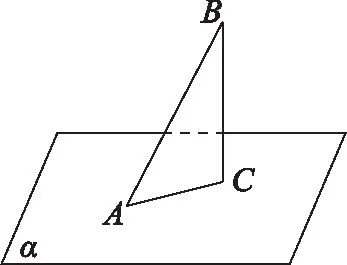
图1

A. 当λ=1时,点C的轨迹是抛物线

B. 当λ=1时,点C的轨迹是一条直线

C. 当λ=2时,点C的轨迹是椭圆

D. 当λ=2时,点C的轨迹是双曲线

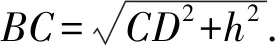
图2

在平面α内,以AD所在直线为x轴,以AD的中垂线为y轴建立平面直角坐标系,如图2所示，设C(x,y),则

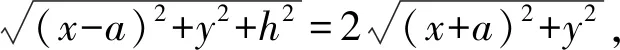
图3

A. 圆 B. 不完整的圆

C. 抛物线 D. 抛物线的一部分

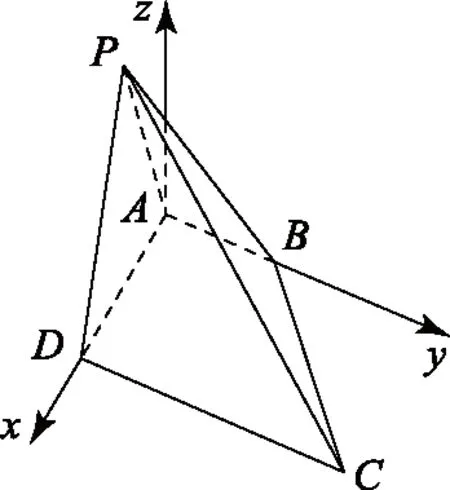
图4

设P(0,y,z) (z≠0),所以

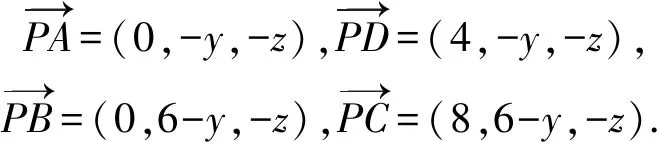
由∠APD=∠CPB,得

将坐标代入并化简得y2+z2+4y-12=0 (z≠0).所以，在平面yAz中,点P的轨迹是不完整的圆.故选B.

2 求运动轨迹的长度

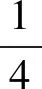
综上，曲线的长度是π+π+π=3π.故选D.

图5

3 求运动区域的面积

设直线l∥BC,延长OG交l于K,连接DK,则∠DKO是点D的平面Γ与底面ABC所成锐二面角的平面角.

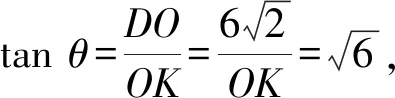
由对称性可知圆内含有3个与△OEF全等的三角形,则还有三个与扇形OEH相同的扇形,则

3∠EOH=360°-3×60°=180°,