A New Robust Adaptive Neural Network Backstepping Control for Single Machine Infinite Power System With TCSC

Yanhong Luo,, Shengnan Zhao, Dongsheng Yang,, and Huaguang Zhang,

Abstract—For a single machine infinite power system with thyristor controlled series compensation (TCSC) device, which is affected by system model uncertainties, nonlinear time-delays and external unknown disturbances, we present a robust adaptive backstepping control scheme based on the radial basis function neural network (RBFNN). The RBFNN is introduced to approximate the complex nonlinear function involving uncertainties and external unknown disturbances, and meanwhile a new robust term is constructed to further estimate the system residual error,which removes the requirement of knowing the upper bound of the disturbances and uncertainty terms. The stability analysis of the power system is presented based on the Lyapunov function,which can guarantee the uniform ultimate boundedness (UUB) of all parameters and states of the whole closed-loop system. A comparison is made between the RBFNN-based robust adaptive control and the general backstepping control in the simulation part to verify the effectiveness of the proposed control scheme.

I. INTRODUCTION

WITH the increasing scale and complexity of modern power systems, the issue of grid security and stability has become increasingly prominent. Undoubtedly, all power systems are driven by dynamic safety and stable operation,which makes research and development of power systems.The safety control theory and technology are becoming more and more important [1]. In recent years, thyristor controlled series capacitor (TCSC) has been used as a flexible AC transmission system (FACTS) device to change the apparent reactance smoothly and quickly. It has the function of reducing the subsynchronous resonance (SSR), suppressing the damping low-frequency oscillation and improving the transient stability in the operation and control of the power system [2]-[4].

In the actual operation, the single machine infinite power system is often affected by external unknown disturbance and parameter uncertainty, which leads to the decline of system dynamic stability and poor robustness. Therefore, it is necessary to design a nonlinear robust controller to improve the dynamic response performance of the system. At present,research on control algorithms in power systems containing TCSC has yielded many scientific research results. In [5], a robust nonlinear co-ordinated generator excitation and TCSC controller is proposed to enhance the transient stability of power systems. Reference [6] uses the linear quadratic Gaussian (LQG) to design the robust TCSC controller for power system oscillation damping enhancement, which can effectively dampen power system oscillations. The above methods ignore the nonlinear characteristics of the power system, and require that the system model must be accurate and the operating conditions are unchanged. In [7], the nonlinear optimal predictive control theory is applied to improve the transient stability and dynamic performance of the power system. The influence of system parameter uncertainties on the control algorithm is not considered. In [8],the nonlinear PI predictive control method is applied, and the uncertainties of the power system are considered to ensure the stability of the closed-loop system under the nonlinear controller. The influence of external unknown disturbances on the system is not considered. References [9] and [10] apply the backstepping method to design the control law, which is adaptive to unknown parameters, uncertain disturbances and model errors. The traditional inversion control is based on the principle of deterministic-equivalence and is used for the control of special structures. In the system, using this method in the recursive design process of the robust controller, there will be a large number of differential operations. In [11], an indirect fuzzy adaptive backstepping control method is applied to design a nonlinearL2gain disturbance attenuation controller with parameter update law. The design process is complex and the storage function of the constructed system is also a difficult problem. In [12], the sliding mode adaptive control method is applied to avoid the state oscillation caused by the coupling of the parameter estimator and the system state. Compared with the adaptive backstepping control, the time to reach the steady state is greatly shortened. When the sliding mode control is close to the sliding surface, factors such as speed, inertia, acceleration, and switching surface need to be considered, and the switching function has a dead zone. An unpredictable chattering interval may be formed in the actual control process.

The combination of artificial neural network and nonlinear control has become a research hotspot in recent years. In [13],the adaptive neuro-fuzzy inference system and the Levenberg Marquardt (LM) artificial neural network algorithm are used to suppress the frequency oscillation and improve the dynamic performance of the power system. In [14], the traditional PID control combined with the radial basis function neural network (RBFNN) is applied to design nonlinear adaptive damping controllers. The controller not only has the characteristics of traditional PID, but also can adjust the parameters of the PID controller online by using the Jacobian matrix information identified by RBFNN, and has strong adaptability to changes in system operating conditions.

In this paper, considering the above problems, an RBFNNbased robust adaptive backstepping controller is proposed.And through the numerical simulation, the dynamic response performance of the proposed controller is compared with that of the general backstepping controller. The results show that the obtained system states converge faster than that by the general backstepping method.

The contribution of this paper can be summarized as follows:

1) It is the first time that the RBFNN is introduced to the robust adaptive backstepping control scheme for the single machine infinite power system with TCSC, which is applied to approximate complex nonlinear functions including system model uncertainty, nonlinear time-delay and external unknown disturbance without knowing the upper bound of the disturbance and uncertainty terms.

2) An online updating robust term is proposed to reduce the residual error of the system to ensure the uniform ultimate boundedness of all the weight parameters and states of the whole closed-loop system without knowing the upper bound of the adaptive parameter. The ideal weights of neural networks and the adjusting rule of the adaptive parameter can also be updated online.

3) Introducing inequalities 0 ≤|x|-xtanh(x/ς)≤0.2785ς,for ς ＞0, avoids the appearance of chattering and obtains a smooth robust adaptive control law.

A. Modeling of Single Machine Infinite Power System with TCSC

Fig. 1. A single machine infinite power system structure diagram with TCSC.

Consider the single machine infinite power system with TCSC shown in Fig. 1 . Assuming that the generator is represented by a constant voltage source after transient reactance, and the TCSC device can be regarded as an adjustable reactance connected in series to a node of the power system transmission line, the mathematical model of the TCSC system can be established as follows [15]:

whereThe generator q-axis transient potentialand the prime mover output mechanical powerPmare set as constants in the normal modeling process. The electromagnetic transient process on the transmission line and the active power loss on the transformer transmission line resistance are negligible. The physical meanings represented by the parameters in(1) are given in Table I.

TABLE 1 THE PHYSICAL MEANING OF EACH PARAMETER

λis the TCSC controller gain factor (λ ＞0) anduis the equivalent control input for the TCSC controller.

In physical significance of parameters, time-delaydis caused by the differences between triggering time and turn-on time of its thyristor controller [16], [17].

Considering that the generator damping coefficientDis difficult to measure accurately in the actual operation of the power system,Dcan be regarded as an uncertain parameter,that is, θ is an uncertain term.

Considering that the power system may be affected by external unknown disturbances during operation, such as superposition perturbation on the system admittance and uncertain disturbances on the generator rotor due to aging of the circuit components of the system, when the rotor of the generator is displaced, an axial thrust is generated. If it is not adjusted in time, it will affect the normal operation of the generator rotor, and if it is serious, it will damage the generator. This is not conducive to the safe and stable operation of the power grid. Based on the above considerations, letA=[A1,A2]Tbe the unknown disturbances superimposed on the generator rotor and the system admittance, whereA1andA2are unknown disturbance functions in spaceL2, and satisfy |Ai|≤Λi,i=1,2, Λi＞0.

Define the state variable of the system asx1=δ-δ0,x2=ω-ω0,x3=ytcsc-ytcsc0. According to the structure of (1),

Therefore, the mathematical model (1) of the TCSC system can be transformed into the following model:

The stable operating balance of the system isand the system state variable isx=[x1,x2,x3]T. For the case where the system has uncertainty and is affected by external unknown disturbances, we propose a robust adaptive backstepping controllerubased on RBFNN, the state variablex(t)of the system asymptotically converges to 0, i.e.,limt→∞x(t)=0. That is to say, whether the system is changed in operating conditions, the parameters are uncertain, or is subject to external unknown disturbances, the rotor power angle δ, the rotor angular velocity ω and the system admittanceytcscasymptotically converge to their corresponding operational steady-state values δ0, ω0,ytcsc0. At this time, the dynamic stability of the single machine infinite power system is guaranteed.

B. RBFNN-Based Robust Adaptive Backstepping Controller Design

The robust control model of a single machine infinite power system with TCSC (2) has uncertainty and is affected by external unknown disturbances, therefore, an RNFNN-based robust adaptive backstepping control scheme is proposed.Meanwhile a sufficient condition for stable operation of the system and an adaptive update law of RBFNN estimation error are obtained. The overall structure of the control system is shown in Fig. 2.

The first step is to define the coordinate transformation of the state variable as follows:

α1and α2are intermediate virtual control quantities.Construct the first Lyapunov function as follows:

Fig. 2. Overall structure diagram of control system.

Deriving the timeton both sides of (4), we obtain

Define intermediate virtual control α1=-c1z1, wherec1is a constant to be designed andc1＞0 . Substituting α1with (3)into (5) yields

According to (2) and (3),z2is derived with respective to timetto obtain

In the second step, construct the second Lyapunov function as follows:

wherek1is a constant to be designed andk1＞0.

The two sides of (8) are simultaneously derived with respective to timetto obtain

Based on (3), we can obtain

Then

Due to the uncertainty of the system and the influence of external unknown disturbances, the complex nonlinear part of(11) is set as a nonlinear function separately as follows:

Then (11) is converted to:

The neural network can be used to approximate the characteristics of any nonlinear function, and the nonlinear functionf1in the model is estimated by the neural network[18]-[20].

Remark 2: Disturbances and uncertainties widely exist in almost all physical systems in the real world, in the form of unknown system dynamics or external perturbations. For the control of such systems, a disturbance observer and related techniques have provided a powerful tool to dynamically estimate and compensate the diverse disturbances and offer desired control performances [21], [22]. Compared with the extended state observer (ESO) [23], neural networks have stronger ability to approximate nonlinear functions and fault tolerance, and, therefore, are especially suitable for multiinput and multi-output systems. In addition, neural networks do not need to model the system, and therefore the neural network model is unlikely becoming very complicated due to the increased complexity of the system. Therefore, the neural network can be used as a black box model of the actual system, using the input and output data of the system for training without knowing the exact system structure.

RBFNN is the popular network in the forward network.Under the condition that there are enough hidden layer nodes,after sufficient learning, any nonlinear function can be approximated with an arbitrary precision, and it has the best approximation ability. In addition, it has a fast convergence speed, powerful noise immunity and repairing capabilities,and the learning method also avoids the local optimal problem[24]-[27]. Therefore, this paper uses an RBFNN to approximate the nonlinear functionf1as follows:

where ε is the estimated error of the RBFNN, and |ε|≤ε*,ε*is an unknown constant.W1is the optimal weight matrix of the RBFNN, which satisfies

where φ (xj) is the basis function of RBFNN [22], and

wherecjis the center of thejth basis function, σjis the width of the basis function, andjis the number of hidden layer nodes. Therefore, (13) can be expressed as

Define the intermediate virtual control amount α2as follows:

wherec2is a constant to be designed andis the estimated value of RBFNN.

Substituting (18) into (17) gives

α2is derived with respect to timetto obtain

According to (2), (3), and (20),z3is derived with respect to timetto obtain

The weight learning rule for the first neural network is given by

where Ξ is a positive definite diagonal matrix to be designed,γ1＞0 is a constant to be designed,W10is the initial weight of the RBFNN.

The third step is to construct the third Lyapunov function as follows:

wherek2is a constant to be designed andk2＞0.andW~1is the approximate error.q(x(τ)) is a nonnegative function.

The two sides of (23) are simultaneously derived with respect to timetto obtain

Substituting (19)-(22) into (24) gives

当前，政府、企业、社会多元共治新格局仍未全面形成，打击侵权假冒工作与人民的殷切期盼还有差距，政府维护市场秩序的公信力仍有待提高。在依法打击侵权假冒案件基础上，及时完善我国相关法律法规和体制机制，营造良好市场营商环境，防止劣币驱逐良币，避免逆向淘汰，从国家、社会、企业和个人视角，多层面、多维度、全方位促进消费市场的健康稳定发展，多措并举保护广大消费者合法权益，已迫在眉睫、势在必行。

Due to the influence of external unknown disturbances,there is a nonlinear term in (25). Since the known terms in(25) are too complicated and difficult to calculate, we put them together to form a nonlinear function as follows:

Then (25) is converted to

Similarly, we use the second RBFNN to approximate the nonlinear functionf2as follows:

where η is the estimated error of the RBFNN, and |η|≤η*,η*is an unknown constant.W2is the optimal weight matrix of the RBFNN.

Therefore, (27) can be expressed as

Define a nonnegative functionq(x(t))=|a2k2(x3z3)(t)|, and then we can obtainq(x(t-d))=|a2k2(x3z3)(t-d)|. An inequality is established as

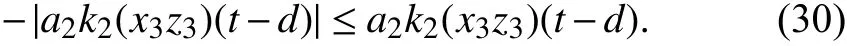
Since neural networks are used to approximate the unknown nonlinear function, the system has residual error, then we letbe the reconstruction error term as follows:

Due to the existence of the error term, we introduce a robust termurto reduce the reconstruction error to ensure the stability of the system as follows:

In summary, we design the final robust control inputufor the system as

wherec3is a constant to be designed andis the estimated value of RBFNN.is the approximate error.

Substituting (30)-(33) into (29) gives

The weight learning rule for the second neural network and the adaptive law for the robust term are given by

where Θ is a positive definite diagonal matrix to be designed,ρ ＞0 is the learning rate, γ2＞0, κ ＞0 are the constants to be designed,W20is the initial weight of the RBFNN.

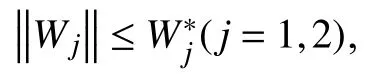
Remark 4: Sensor (measurement) and actuator faults have a significant impact on the control of linear systems, nonlinear systems, and discrete time systems. During the actual operation of the control system, sensor and actuator selfvalidation is a critical step in system control and fault diagnostics. If sensors do not work properly, one cannot rely on their outputs to further deduce system status. Similarly,faulty actuators will not satisfy system performance objectives and may cause disasters in feedback control systems. The reliability of a process machine can be significantly enhanced by introducing a fault-tolerant control system in it [28]-[33].In the next step, we will introduce the sensor (measurement)and actuator faults into the proposed control method and conduct a detailed study.

C. Proof of Stability

Theorem: The robust control model for a single machine infinite power system with TCSC (2), if the control law is(33), and the adaptive learning law of the RBFNN weight online learning algorithm and the adaptive law for robust term are (32), (35) and (36), it can ensure that all parameters and states of the closed-loop system are uniformly and ultimately bounded.

Proof: Select the Lyapunov function as

The two sides of (37) are simultaneously derived with respect to timetto obtain

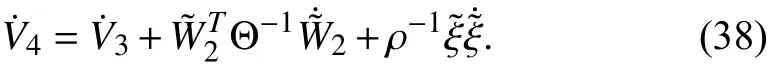
Substituting (34)-(36) into (38), and usingwe get

Substituting (40)-(42) into (39) gives

Multiply both sides of (44) byectto get

Integrate both sides of (45) on [ 0,t] [37]-[39] to get

Combining equations (4), (8), (23) and (37), we can get

Accordi ng towe can get

Accor ding to the definitions of α1, α2, (3) and (48), we can get

According to (46) and letting µ*=2µ/c, we can get

Similarly, the uniform ultimate boundedness of the state variable of the closed-loop system and the weight parameters of the neural network can be derived as follows:

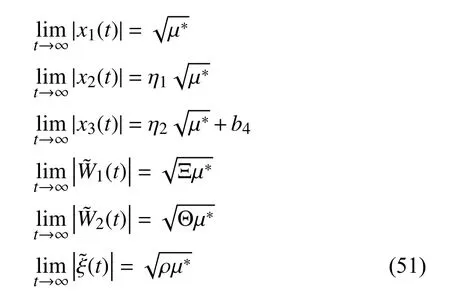
Remark 5: It can be seen from the above proof that the convergence domain of the tracking error, neural network weight parameter and the robust term can be changed by adjusting the parametersc1,c2,c3,k1,k2, γ1, γ2, κ , ς. For example, increasingc1or decreasing ς can reduce the tracking error and the convergence of the neural network weight parameters to the radius, and other parameters can be selected according to needs. So we conclude that the tracking error and neural network weight parameters can converge to an arbitrarily small neighborhood near zero by adjusting above parameters.

D. Numerical Simulation

In order to verify the effectiveness of the proposed method,the presented controller and adaptive updating law are numerically simulated by the MATLAB/Simulink software.

The parameters of a single machine infinite power system containing a TCSC are as follows:H=8,Vs=1.99,=1,Xd=0.88,XT=0.88,XL=0.48,BL-Bc=0.25. We select the controller parameters as follows:λ=1,c1=3,c2=6 ,c3=12 ,k1=1.5,k2=100. The equilibrium states corresponding to δ, ω andytcscare δ0=57.2°, ω0=314.159 rad/s andytcsc0=0.6p.u.. Let the unknown disturbance in theL2space beA1=e-3tsin(4t)sin(5t),A2=e-4tcos(6t)cos(8t), and let the disturbance begin to act on the controlled system (2) at timet.

The number of neurons in the hidden layer of RBFNNs is 9,the center point of the basis function is evenly distributed in interval [-2,+2], the learning gain is ρ=3, the parameters γ1=2, γ2=3, κ=3, the initial value of the neural network

weight isW10=0,W20=0.

Four case studies are performed to simulate the nonlinear TCSC systems with different time delaysdor friction damping coefficientsD. Cases 1-3 aim to compare the stability and robustness of TCSC control systems designed by the proposed RBFNN-based robust adaptive bakstepping(RRAB) method, and the adaptive backstepping (AB) method in [40].dandDare set to 0.01 s and 0.8 p.u. in Case 1, 0.02 s and 0.8 p.u. in Case 2, and 0.04 s and 0.8 p.u. in Case 3,respectively. In Case 4, simulations of our designed TCSC system withd= 0.02 s are performed atD= 0.4 p.u. andD=1.2 p.u., respectively.

The system state variable initial value is set to the following non-zero initial conditions:x1(0)=0.5,x2(0)=2.5,x3(0)=0.1.

Fig. 3 shows the transient response comparisons of δ, ω,

ytcscin Case 1. It can be seen that the transient responses of the state variables of the RRAB controller are faster than those of the AB controller.

Fig. 4 shows the transient response comparisons of δ, ω,ytcscin Case 2. The transient trajectories of the RRAB controller fluctuate less strongly and quickly converge to steady state than those of the AB controller in finite time,suggesting that the proposed RRAB method results in better system performances.

Fig. 5 shows the transient response comparisons of δ, ω,ytcscin Case 3. The result of Case 3 reveals that the proposed method can guarantee that the state variables of the nonlinear TCSC system are globally bounded and transient responses will eventually converge to a stable value regardless of what delay time is considered. A comparison of the transient responses of the RRAB controller in the three cases shows that the transient responses in Case 3 converge more slowly and the system stability is attained in a longer finite time.Similar comparative results are obtained for the AB controller.

Fig. 6 shows the transient response comparisons of δ, ω,ytcscin Case 4. The simulation results are compared to investigate the effect of the friction damping coefficientDon the stability and robustness of TCSC control systems. It can be seen that althoughDtakes different values, the transient responses of the state variables eventually converge to the stable value. The above results show that the proposed RRAB controller has good robustness.

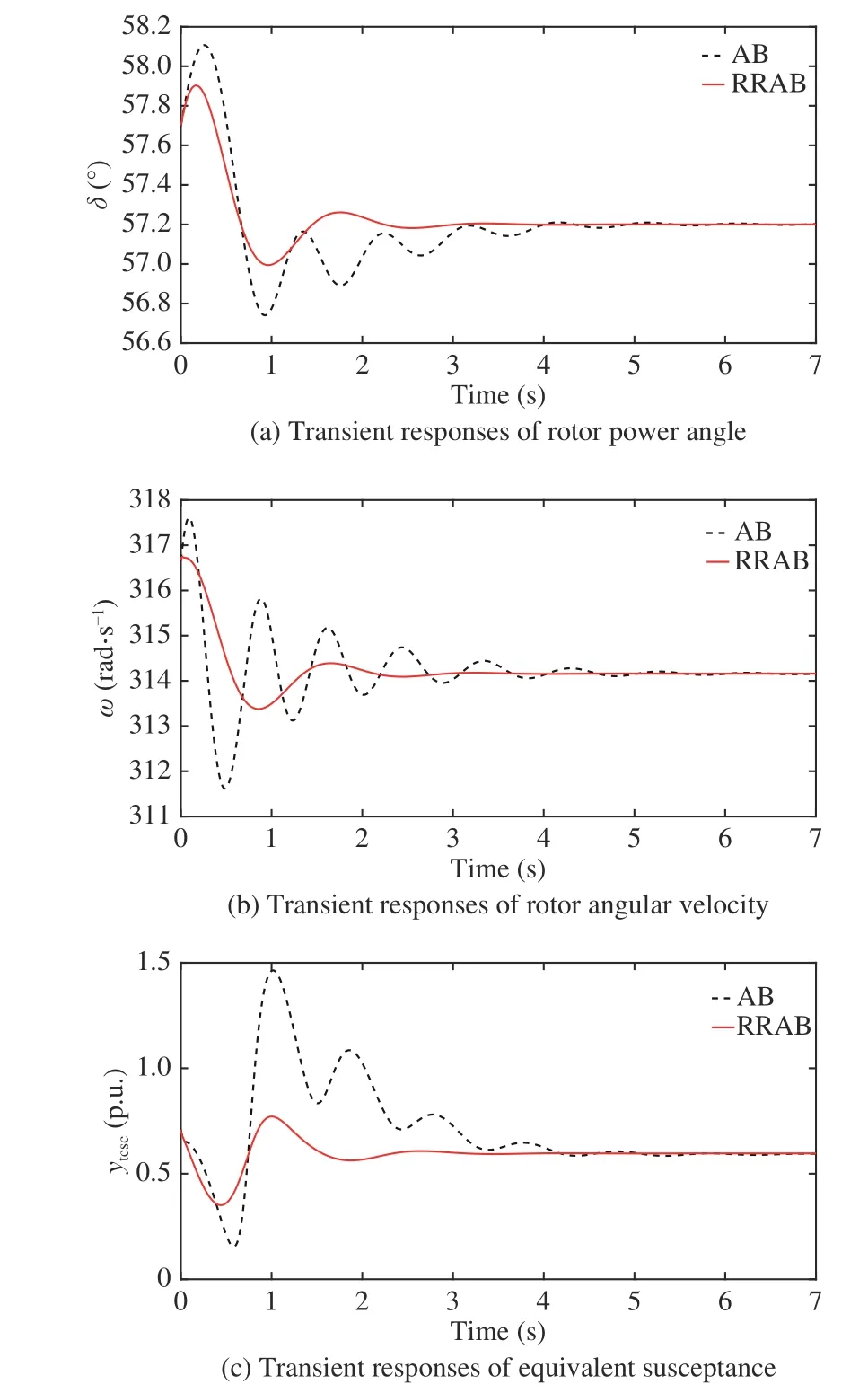
Fig. 3. Transient responses in Case 1.

Fig. 4. Transient responses in Case 2.

Fig. 5. Transient responses in Case 3.

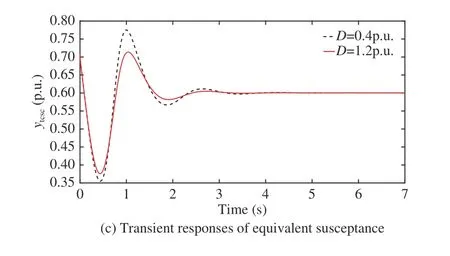
Fig. 6. Transient responses in Case 4.

II. CONCLUSION

In this paper, aiming at the stability control problem of the single machine infinite power system with TCSC, considering the model uncertainty, nonlinear time-delay and the influence of external unknown disturbance, an RBFNN-based robust adaptive backstepping control method is proposed. The simulation results show that the designed controller can achieve stable control of the single machine infinite power system with TCSC and has good robust performance.