基于二次剩余的密钥体制的构造①

(安徽理工大学数学与大数据学院，安徽 淮南 232001 )

0 引 言

随着云时代的到来，许多人将自己重要的信息上传至互联网服务器上，由此而来的互联网通讯与共享的数据安全性备受关注。为确保数据的安全，首先要做的就是信息加密。在密码学中加密的方式众多，公钥密码体制因其独特的优点[1],有着不可代替的作用[2]。当选好加密密钥时，每个明文和每个密文之间的对应关系是双射的。然而，当把明文进行加密时，对于公钥密码体制来说，加密算法的密钥通常是提前公布出来的。所以，一般而言确定的公钥密码体制是很难抵挡住选择明文的攻击。对于公钥密码体制的这一缺憾，1984年Goldwasser和Micali首次提出了概率密码体制的概念[3]，但因膨胀率过大没有实用的价值。文献[4]和文献[5]分别提出了基于顺序和无序序列的多变量概率公钥密码体制，有着良好的随机性，安全性得到保障。

本文基于二次剩余以及概率加密的思想，对概率公钥密码深入研究，构造了一种以二次剩余为基础的多项式加密密钥体制。新构造的二次剩余密钥体制能够很好地抵挡选择明文的攻击[6]，同时它的密文膨胀率低于Blum和Goldwasser提出的BG密码体制的密文膨胀率，且密码体制的安全性不低于RSA公钥密码体制的安全性[7]。

1 基本定义与相关定理

设n是正整数集，Zn={x|0x

定义1.2 若n=p·q，其中p和q为两个互不相同的素数，并且满足p≡q≡3mod4，则称n为Blum数。

定理1.1[8](欧拉定理)若(a,n)=1，则aφ(n)≡1modn。

定理1.3[9]设p和q为两个互不相同的素数，n=p·q，则对任一整数a∈Zn*，有a∈Qn，等价于a∈Qp且a∈Qq。

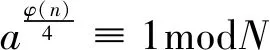
定理1.5[9]设N=p·q为Blum数，a∈Qn，则对于x2≡amodN有：

(1)在模N下有4个平方根

(2)这4个平方根有且仅有一个属于Qn，且

定理1.6 设N=p·q，其中p和q为两个互不相同的奇素数，则分解N计算上等价于求模N的平方根。

2 密码算法设计

2.1 密钥选取

首先：Bob找出两个较大的素数p,q(不能公开)，使得p≡q≡3mod4，同时需要计算Blum数N=p·q

其次：Bob将N公开，作为加密算法中的加密密钥。

最后：Bob将p,q作为解密算法中的解密密钥。

2.2 加密算法

步骤1：在Zn上的n次不可约多项式P(x)=a0+a1x+a2x2+…+anxn，明文M为(a0,a1,…,an)，(a0,a1,…,an)为n次不可约多项式的系数序列。

步骤2： Alice找到Bob提前公布的加密密钥N，作如下计算：

b0≡a02modN

b1≡a12modN

⋮

bn≡an2modN

得到序列B=(b0,b1,b2,…,bn)

x0≡k2modN

x1≡x02modN

⋮

xn+1≡xn2modN

得到序列D=(x1,x2,x3,…,xn+1)

步骤4：再计算出xn+2≡xn+12modN

步骤5：计算E=(b0×x1,b1×x2,…,bn×xn+1)，记c1=b0×x1，c2=b1×x2，…，cn+1=bn×xn+1

步骤6：传送密文C=(c1,c2,…,cn+1,xn+2)给Bob。

2.3 解密算法

步骤1：Bob获得Alice发送的密文C=(c1,c2,…,cn+1,xn+2)之后，根据定理1.5，依次计算：

⋮

得到序列D=(x1,x2,x3,…,xn+1)

步骤3：由序列B=(b0,b1,b2,…,bn)以及定理1.5可得：

⋮

步骤4：最终解出明文M=(a0,a1,…,an)，因此Bob就破译了Alice发给他的密文。

3 密码算法的分析与评价

3.1 正确性分析

3.2 安全性分析

从加密解密过程中不难看出，如果敌方截获密文和加密密钥，想要得到明文的相关信息，就一定要去计算模N下的平方根，由定理1.6，该问题归结为分解大合数为素数之积的问题，故该加密算法的安全性就等同于RSA加密算法的安全性。同时，我们在加密过程中添加了随机数k，使得密文具有随机性。即我们对一样的明文使用一样的加密密钥，选取不同的随机数进行加密时所获得的密文是有差异的，有效地防止了选择明文攻击。所以，这种基于二次剩余的多项式加密的概率公钥密码体制的安全性不低于RSA密码体制的安全性。

3.3 性能分析

从加密解密过程可知，本文设计的概率公钥密码体制主要涉及计算数模的平方根运算，接下来就对其性能进行分析，主要包括密文膨胀率以及加解密效率两大方面。

3.3.1 密文膨胀率

3.3.2 加解密效率分析

这种基于二次剩余构造的密钥体制在加密时的时间主要是用在两次平方求余的计算上，解密是用在两次模的计算上，其时间复杂度略高于BG密码体制，而小于RSA等公钥密码体制的时间复杂度[11]O(k3)。因此，新的概率公钥密码体制的加解密效率较高。

4 结 语

公钥密码体制是密码学中较为普遍且广泛应用的加密体制[12]。对于公钥密码算法的加密密钥而言，通常是提前公布出来的[13]。所以公钥密码体制是抵挡不住选择明文的攻击。本文以大数因数分解的困难性和模Blum数的二次剩余求平方根的不易性为理论基础，引入随机数，构造了一种以二次剩余为基础的多项式加密密钥体制。同时，论证了它密码体制的安全性是不会低于RSA的安全性。利用给出的密码体制，加解密的效率较高，当传输的明文较长时，它的密文膨胀率近似为1。此外，新构造的密钥体制是针对多项式的概率加密，若是把多项式的系数序列表示成二次型的矩阵，那么新构造的密钥体制对于图像加密也同样适用。