失效树模型在弧形钢闸门可靠性评估中的应用

杨娟娟，洪 伟，吴 振，杜子立，王 颖，林立旗

（1.水利部水工金属结构质量检验测试中心，河南 郑州450044；2.水利部综合事业局，北京100053；3.山东省水利科学研究院，山东 济南250013）

0 引言

水工钢闸门在水电枢纽中起着泄洪、拦水、引水发电的重大作用，因此对水工钢闸门可靠性进行评估的工作具有重要意义。当前，针对水工钢闸门展开的评估方法主要集中在闸门结构安全方面[1-4]。由于影响水工钢闸门可靠性的因素存在较大不确定性，均为随着时间或空间变化的随机函数或过程。因此，采用失效概率的方式对其进行反映较为合理。为了满足闸门结构体系可靠性评估需求，本文将失效树分析模型引入闸门体系可靠性评估中，建立了弧形钢闸门结构体系可靠性评估模型，并以某二级水电站弧形钢闸门为研究对象，进行了演算分析，借此来实现对弧形钢闸门结构体系的可靠性评估。

1 失效树分析理论及方法

失效树分析方法，也称为故障树分析方法，是可靠性分析领域最常用的方法之一[5]。失效树分析法主要是用来识别系统中可能存在的故障及事件，并依据资料分析该故障引起整个系统发生故障的可能性。通过失效树分析可以找到系统失效的真正原因。

1.1 定性分析

一般而言，导致一个系统失效的原因可能有A1，A2…等中的一个或多个。在失效树分析中，称系统失效为顶事件。顶事件与导致系统失效的原因A1，A2…之间存在诸多逻辑关系，这些逻辑关系称之为逻辑门。通常逻辑门主要有3种，即“或门”“与门”“非门”。“或门”代表的逻辑关系为任何一个事件Ei的发生都能导致事件A的发生。“与门”代表的逻辑关系为所有事件Ei都发生才导致事件A发生。“非门”代表的逻辑关系为事件Ei与事件A不会同时发生且状态总是相反。3种逻辑门的标识表达如图1所示。

图1 逻辑门表达符号

在失效树分析中，可能导致顶事件发生的最低限度事件（可同时发生）的集合，称为最小割集。一个最小割集代表系统的一种失效模式，故而，失效树定性分析是建立在最小割集的基础上的，因此，最小割集中的底事件类型是需要注意的重要因素。

1.2 定量分析

定量分析主要是为了计算顶事件发生的概率。假设n为某一失效树中不同底事件的个数。

Y（t）=[Y1（t），Y2（t），…Yn（t）]为系统的状态向量。在t时刻，顶事件状态用变量ψ[Y（t）]描述：

对于有n个底事件的失效树，若已知各个底事件及顶事件发生的状态，可以得到：

变量ψ[Y（t）]，称之为失效树的结构函数。

假设qi（t）为t时刻底事件i发生的概率（i=1，2，…，n），则qi（t）的定义为：

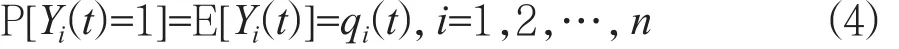
假设Q0（t）为t时刻顶事件发生的概率，则Q0（t）的定义为：

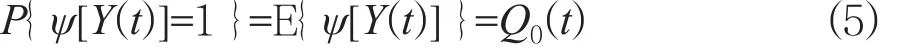
在此，需要注意的是在失效树中，顶事件或者底事件其内涵是系统工作的实际状态。例如，“在t时刻底事件i发生”其实是指t时刻底事件i的系统处于的实际状态。

令pi（t）为第i个系统单元在t时刻处于正常工作的概率，qi（t）为第i个系统单元在t时刻的不可靠度，Q0（t）为t时刻系统的不可靠度，则：

假定所有的底事件都是相互独立的，底事件和顶事件都只有两种状态，即发生和不发生，也就是说组成弧形钢闸门结构体系的部分或构件只有两种状态，即正常和失效，则根据底事件发生的概率，按失效树的逻辑结构逐步向上运算，即可得顶事件发生的概率。

2 弧形钢闸门的失效树分析模型

弧形钢闸门结构较为复杂，可视作系统。对于系统的可靠度分析，依赖于对其底事件的分析。在闸门在结构系统可靠度分析中，由于系统失效树的建立，使得对全系统的可靠度分析有了可能。建立弧形钢闸门失效树分析模型的过程步骤如下：

（1）确定顶事件。弧形钢闸门其主要功能是挡水及泄水，以实现水利工程蓄水、泄洪、发电等功能。因此，顶事件就应该是弧形钢闸门功能障碍，即弧形钢闸门不能开启或关闭，记顶事件为F。

（2）确定顶事件的最小割集。弧形钢闸门一般由门叶结构、闸门滑槽的埋件与启闭机械设备3大部分组成。因此对于顶事件的最小割集的确定应是包含弧形钢闸门自身结构原因及运行的周边条件。当弧形钢闸门门体结构出现损伤、启闭系统故障时，弧形钢闸门均不能完成开门或闭门功能，因此这二者必是顶事件的最小割集。在弧形钢闸门的安装过程中，也存在出现安装缺陷的情况，因此安装失误也为最小割集。至此，顶事件的全部最小割集都已经得到，分别记作：门体结构损伤A1、启闭机故障A2、布置缺陷A3，逻辑图见图2。

图2 弧形钢闸门顶事件及其最小割集失效树

（3）确定各最小割集的底事件及基本事件。上文确定了弧形钢闸门失效分析的顶事件是弧形钢闸门不能正常开启或关闭，顶事件最小割集有3个事件，即门体结构损伤A1、启闭机故障A2、布置缺陷A3，如图 3、图 4、图 5 所示。

图3 事件“门体损伤”失效树

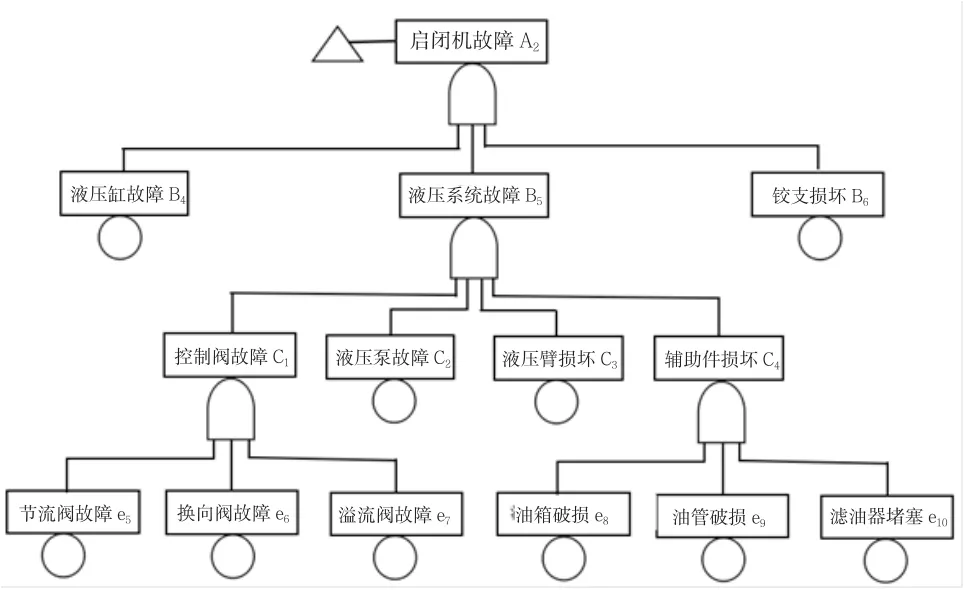
图4 事件“启闭机故障”失效树

图5 事件 “布置缺陷”失效树

3 基于失效树模型的弧形闸门可靠性评估

某流域二级水电站装机规模为7万kW，正常蓄水位735.00 m以下，水库库容约等于17万m3。该水电站导流冲砂洞工作闸门为双主横梁直支臂圆柱铰弧形钢闸门，尺寸为5.0 m×7.0 m（宽×高），正常蓄水位为19 m，设计水位为20.2 m，校核水位为23.5 m，设计使用年限30年。本文以该电站弧形钢闸门为例，结合该弧形闸门的安全检测材料，开展可靠性评估分析。

3.1 闸门失效概率的计算

由前文所建立的弧形钢闸门失效树分析模型可知，确定该弧形闸门失效顶事件的概率，需计算每一个底事件的发生概率。

（1）事件“门体损坏”发生概率的计算。如图3所示的事件“门体损坏”的失效树分析模型。“门体缺陷”记事件A1，其下有割集事件：门体失稳B1、主梁失稳B2、支臂失稳B3，最小底事件一共有5件，即事件B1、e1～e4。采用上行法来确定事件A1的发生概率。

依据现场实测数据，该弧形钢闸门结构静应力测试最大拉应力值为85 MPa，最大压应力值为-140 MPa，运动状态结构应力测试最大拉应力值发生在闸门2.7 m开度，其测试值122 MPa，最大压应力值发生在闸门0 m开度时，其测试值-169 MPa，且在闸门启闭期未出现共振现象，其结构动态性能满足工程需要，因此主梁、面板、支臂是较为稳定的。对于事件“面板失稳B1”“主梁失稳B2”“支臂失稳B3”而言，其整体或局部构件的稳定性按照文献[6][7]标准中的方法进行稳定性校核，校核结果均满足安全条件，因此事件B1、e1～e4在当前状态下不会发生，出现结构失稳导致弧形钢闸门门体不正常启闭的概率为0%。故事件A1发生的概率：

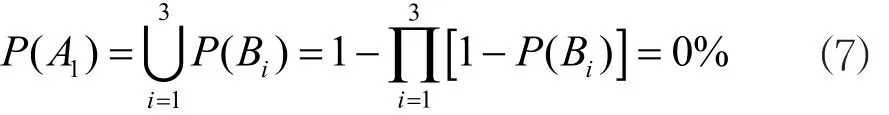
（2）事件“启闭机故障”发生概率的计算。该弧形钢闸门启闭机一直维护良好，各项参数显示正常，在使用记录中未出现任何不良记录。因此，在此认为事件B4、e5～e10发生概率均为0%，据此可以计算事件“液压系统故障B5”发生概率为0%。对于事件“铰支损坏B6”，该弧形钢闸门支铰处存在一定程度的锈蚀，对于固定螺栓及支铰结构的强度有影响，锈蚀厚度平均为1.2 mm，依据文献[8][9]提供的计算方法，可以计算事件“铰支损坏B6”发生的概率为0.1%。由此，可计算事件A2发生概率为：

（3）事件“布置缺陷”发生概率的计算。现场采用姿态测试仪器对该弧形钢闸门做过姿态检测，未发现该弧形钢闸门存在姿态不正的情况，因此事件“姿态不正B7”发生的概率为0%。对于制造质量，该弧形钢闸门出厂取得了安全许可证，在使用过程及检测过程中，未发现较为明显的外形及焊缝缺陷，故而，事件e11～e12发生的概率均为0%。在该弧形钢闸门的启闭过程中，未出现流态恶劣的情况，且在各开度下下支臂翼板的振动比腹板强烈，下支臂靠近横梁处的振动最大，在启闭过程中没有出现门叶共振现象，故事件“共振损伤B9”、“流态恶劣B10”发生的概率均为0%。因此事件“布置缺陷A3”发生的概率为：

至此，顶事件的全部最小割集事件的发生概率都已经确定：事件“门体结构损伤A1”发生概率为0%；事件“启闭机故障A2”发生概率为0.1%、事件“布置缺陷A3”发生概率为0%。因此，顶事件“闸门故障F”发生的概率为：

3.2 闸门可靠度指标的确定

由前文可知，依据所建立的弧形钢闸门的失效树分析模型，只需要对各个底事件进行分析，求得其失效概率qi（t），就可以求得弧形钢闸门结构系统在t时刻系统的不可靠度为Q0（t），从而弧形钢闸门结构系统的可靠度为1-Q0（t）。可靠度指标β是度量结构可靠性的数量指标，也是标准正态分布反函数在可靠概率处的函数值。因此，依据定义，可以实现弧形钢闸门结构系统可靠概率与可靠度指标β换算。假设求出的弧形钢闸门结构系统的失效概率（即为不可靠度）为Q0（t）、闸门结构系统的可靠概率为1-Q0（t），则可靠度指标β可由下式求出：

根据文献[10]，结构的可靠度水平应根据结构构件的安全级别、结构及其构件的失效模式及经济因素综合来确定，依据结构的安全性及实用性应设置不同的可靠度水平，具体安全级别构件的目标可靠度指标如表1所示。

表1 目标可靠度指标βT

一般而言，当闸门结构或构件的实际可靠度指标β小于极限状态值βL，则认定闸门结构失效，不能再使用。因此，将该极限状态值βL作为结构最低可靠指标限值，可以对弧形钢闸门的安全进行评估。一般认为βL=0.8βT比较适用[11-13]。按照《DL5108-2003水电枢纽工程等级划分及设计安全标准》电力标准划分，该弧形钢闸门所在的二级水电站为Ⅲ等，属于中型工程的工程规模，泄洪冲砂洞的安全级别为III，其破坏类型应为二级破坏。因此，该弧形钢闸门结构目标可靠度指标βT为3.2。由此可计算该闸门结构的极限状态可靠度指标：

由式（1）～（10）可知，顶事件“闸门不能开启或关闭F”发生的概率为0.1%，即弧形钢闸门结构系统不可靠度为 0.1%。依据式（1）～（11）所建立弧形钢闸门系统可靠概率与可靠性指标的计算关系，可计算得到该弧形钢闸门可靠度指标β为：

由前文内容可知，该弧形钢闸门安全等级对应的可靠度指标限值βL为 2.56，则：β＞βL，因此该弧形钢闸门是满足安全要求的，这与对该闸门进行安全检测所得结论是较为一致的。

4 结论

对于弧形钢闸门而言，其结构体系的可靠性应不仅仅与其载荷、抗力有关，还要考虑其服役环境、有接触的上下结构等因素。因此，采用工程结构可靠度理论的研究方法虽较为精确、可信度更高，但其对水工弧形钢闸门结构体系的可靠性分析存在较多困难。本文将水工钢闸门作为一个系统，引入失效树分析方法，建立了水工弧形钢闸门结构体系的可靠性分析模型，并开展了具体算例分析，对弧形钢闸门的可靠性进行了评估。虽然失效树模型是在理想状态下建立的，且存在一定的主观性，但为水工弧形钢闸门结构体系的可靠性评估分析提供了一种研究思路。随着今后失效树模型研究应用的深入与完善，失效树分析模型将会在水工弧形钢闸门可靠性评估研究领域发挥更为重要的作用。