基于屈服线理论的混凝土护栏计算研究
2020-02-28董佳霖马芹纲
董佳霖,马芹纲
(浙江省交通规划设计研究院有限公司 杭州市 310000)
0 引言
护栏作为桥梁一项重要附属结构,其合理安全的设计是保障交通安全和人民生命财产的重要设施。据美国一项调研发现,每年因车辆与护栏碰撞事故死亡人数约14000人,受伤人数高达100万人,直接或间接损失高达800亿美元[1]。可见,车辆护栏碰撞分析、护栏设计理论及设计方法的研究至关重要。
国内对桥梁混凝土护栏的研究主要集中在碰撞模型、碰撞仿真模拟、护栏-车辆动力响应等方面,大多是基于能量守恒的理论分析[2-3]和碰撞试验、计算机模拟[4-5]等。石红星等人[6]根据动量定理,以汽车与护栏发生碰撞时动能全部转化为汽车倾覆的势能为极限状态,提出了护栏高度与冲击力的简化计算方法;闫书明[7]通过一段48m的护栏试验段足尺试验和有限元动态模拟,验证某单坡面混凝土护栏具有400kJ防撞能力;余江等人[8]建立了护栏局部和整体受力的有限元模型,研究护栏在不同荷载作用模式下的应力分布,对比分析了集中荷载和均布荷载作用下的护栏受力,确定了设计荷载的分布宽度;赵鸣等人[9]建立了车-护栏连续系统分析模型,考虑车和护栏的共同变形,采用Runge-Kutta法模拟汽车的运行轨迹、车体转角、加减速度等。
屈服线理论基于结构塑形变形范畴,被广泛应用于预应力混凝土双向板[10]、节点局部受力[11]等结构设计中。在混凝土护栏设计方面,美国AASHTO-2012[12]中最早采用屈服线理论进行护栏设计,国内卫军等人[13]通过车辆-护栏碰撞动力响应分析,获得撞击过程的碰撞力和分布长度,通过分析护栏不同的屈服破坏模式,建立车辆碰撞护栏的塑形变形屈服线,确定护栏抗碰撞设计方法。
以护栏合理设计、护栏安全性能评价为出发点,详细介绍了基于屈服线理论的混凝土护栏设计理论和设计方法。
1 计算原理
1.1 基于屈服线的设计原理
规范中规定混凝土护栏构件的设计采用屈服线分析和强度设计的理论[14]。屈服线分析方法原理为:模拟车辆以一定的动能和碰撞角度撞击护栏,假设护栏为刚体,在碰撞过程中不发生位移,根据能量守恒原理建立车辆撞击护栏过程的能量方程。根据护栏可能出现的塑形变形破坏模式,按结构动力学原理和能量守恒原理求解护栏极限承载力、冲击力分布长度(即屈服线长度)。对于不同护栏等级,最小的极限承载能力所对应的破坏变形即为护栏设计控制破坏模式[12]。设计中按照护栏配筋,计算出护栏对横向碰撞荷载的抗力标准值,抗力值应大于横向碰撞力设计值。
碰撞发生在护栏标准段和端部时破坏模式分别见图1(a)、图1(b)。碰撞发生在标准段时,护栏屈服面(破坏面)沿车辆碰撞中心对称分布,护栏内侧与外侧均发生屈服破坏,破坏面呈现楔形,屈服线范围内内侧两条破坏面直通护栏顶部与桥面板交界处,在向外侧冲击的作用下,护栏板顶端发生的横向位移为,外侧有一条撞击破坏面。碰撞发生在护栏端部时,屈服面自车辆碰撞中心沿纵向向护栏中部延伸,护栏内侧发生屈服破坏,外侧则未达到屈服破坏。
1.2 计算公式
碰撞发生在护栏标准段时,护栏对横向荷载的抗力标准值和屈服线发生的临界长度的计算公式为:
(1)
(2)
当碰撞发生在护栏端部或伸缩缝处时,计算公式为:
(3)
(4)
式中:H为护栏的有效高度(m);Lc为屈服线破坏分布的纵向长度(m);Lt为碰撞荷载分布的纵向长度(m);Rw为护栏的总的横向承载能力(kN);Mw为护栏关于其竖向轴的弯曲承载力矩(kN·m);Mb为护栏顶部除Mw之外的横梁附加弯矩承载力矩(kN·m);Mc为悬臂型护栏关于桥梁纵轴的弯曲承载能力(kN·m/m)。
《公路交通安全设施设计规范》(JTG D81-2017)中对混凝土护栏横向碰撞荷载的设计值及分布长度的规定详见表1。
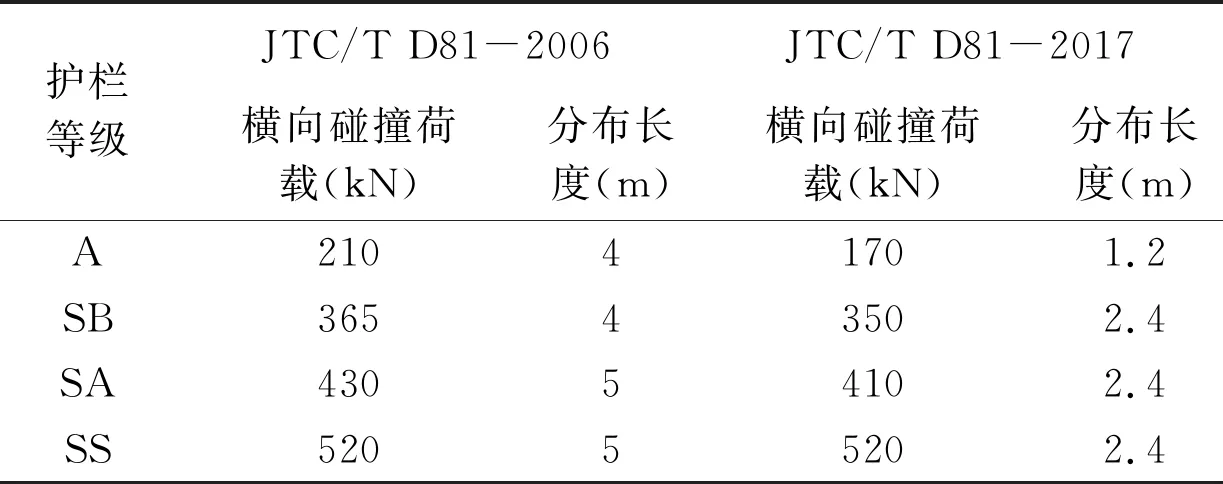
表1 护栏横向碰撞荷载及分布长度取值表
1.3 设计流程
基于屈服线理论的混凝土护栏设计流程见图2。
2 SS级混凝土护栏计算示例
以某SS级护栏为例,详细介绍基于屈服线理论的混凝土护栏设计方法。护栏的横断面如图3所示,护栏高1.3m(含20cm铺装厚),纵向点筋直径为12mm,沿护栏高度共有16根;护栏箍筋直径为16mm,沿行车方向10cm间隔布置。
2.1 护栏标准段验算
(1)Mw计算
Mw是指护栏关于其竖向轴的弯曲承载力矩,Mw的计算截面如图4所示(图中di为编号为i的钢筋所在截面的有效高度,如d1为1号钢筋至护栏内侧混凝土边缘的距离)。沿护栏纵向共布置16根C12钢筋,其中1~8号为外侧钢筋编号,9~16为内侧钢筋标号。由于沿护栏高度方向护栏的宽度不同,因此分别计算每根钢筋的抗弯承载力。
根据矩形截面受力平衡,有:
fsdAs=fcdbx(对于竖向轴而言,b为护栏高度1.3m)
受压区高度为:
该矩形截面的抗弯承载力为:
其中,φ为结构重要性系数,取值为1.0。
碰撞发生在护栏标准段时各根钢筋的抗弯承载力计算如表2所示。
根据屈服线理论,碰撞发生在护栏标准段时,在护栏内侧产生两条屈服线,护栏外侧存在一条屈服线,因此护栏关于其竖向轴的弯曲承载力矩按照内侧钢筋承载力2/3和外侧钢筋承载力1/3加权平均:
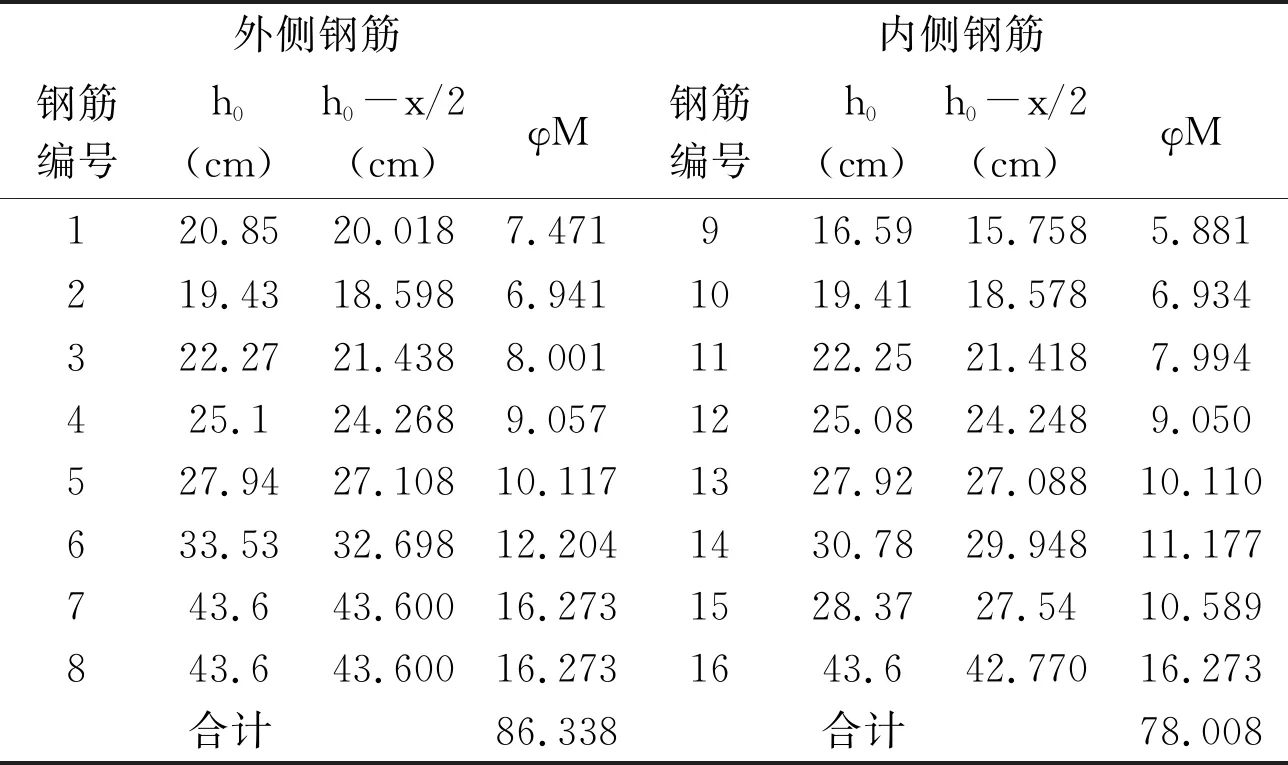
表2 护栏标准段Mw计算表(弯矩单位:kN·m)
(2)Mc计算
Mc是指护栏关于桥梁纵轴的弯曲承载力矩,沿纵桥向取1m护栏截面作为Mc计算截面,箍筋的间距为10cm,共计10根C16钢筋。因为护栏宽度不同,以护栏内侧折点作为划分点,将护栏沿横断面分为上部和下部两个计算截面,计算图示如图5所示。选取护栏上下截面的有效宽度(箍筋中心至另一侧混凝土边缘的距离)的平均值作为计算截面的有效宽度,按照矩形计算表格见表3。
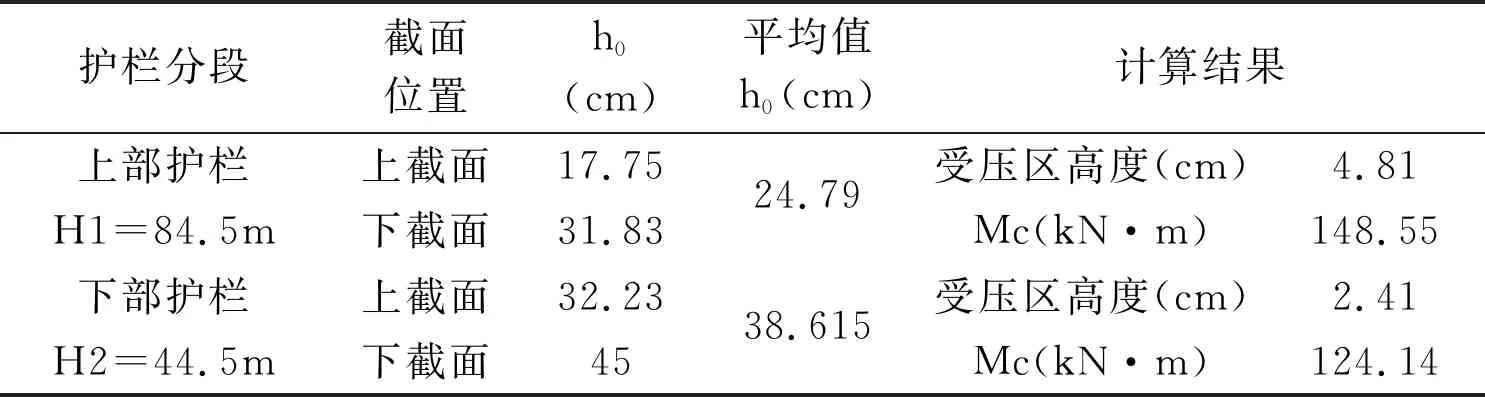
表3 护栏标准段Mc计算表
按照矩形截面受弯构件分别计算护栏上、下部截面受压区高度和弯矩承载能力。由于护栏下部箍筋并未形成完整的圆箍,这里参照美国AASHTO-2012规范并结合我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》对箍筋的抗弯承载能力进行折减。
对于C50混凝土(桥面板)中的HRB400钢筋,受拉钢筋直端最小锚固长度为30d,受拉钢筋弯钩端的最小锚固长度为25d。对于伸入至桥面板的箍筋N1,由于存在如图6所示的90°弯钩,相当于增加了5d的锚固长度,因此该环形钢筋的折减系数为:
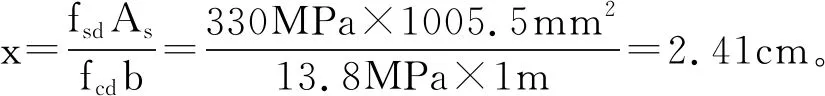
护栏下部的抗弯承载力为:
上部、下部计算的Mc值按高度取加权平均值为:
(3)护栏抗力Rw计算
对于无横梁的钢筋混凝土,Mb=0。SS级护栏屈服线长度Lt=2.4m,将上述Mw、Mc计算结果分别带入式(1)、式(2),破坏的临界长度和护栏对横向荷载的抗力标准值分别为:
经计算,护栏标准段满足抗横向碰撞的要求。
2.2 护栏端部验算
(1)Mw计算
因碰撞发生在护栏端部时,仅护栏内侧发生屈服破坏,护栏关于其竖向轴的弯矩Mw仅考虑护栏内侧钢筋的抗弯作用,其破坏模式如图7所示。假定屈服线的临界长度为2.6m。对于C30混凝土,受拉钢筋直端的锚固最小长度的35d(42cm),即当屈服线内侧纵向点筋的长度大于35d时才能完全发挥作用,小于时按照实际长度/最小锚固长度对钢筋面积进行折减。
折减后能提供护栏关于竖轴抗弯承载力的钢筋面积为866.59mm2,因此受压区高度为:
分别计算纵向点筋所在截面的抗弯承载能力,Mw的详细计算过程见表4。
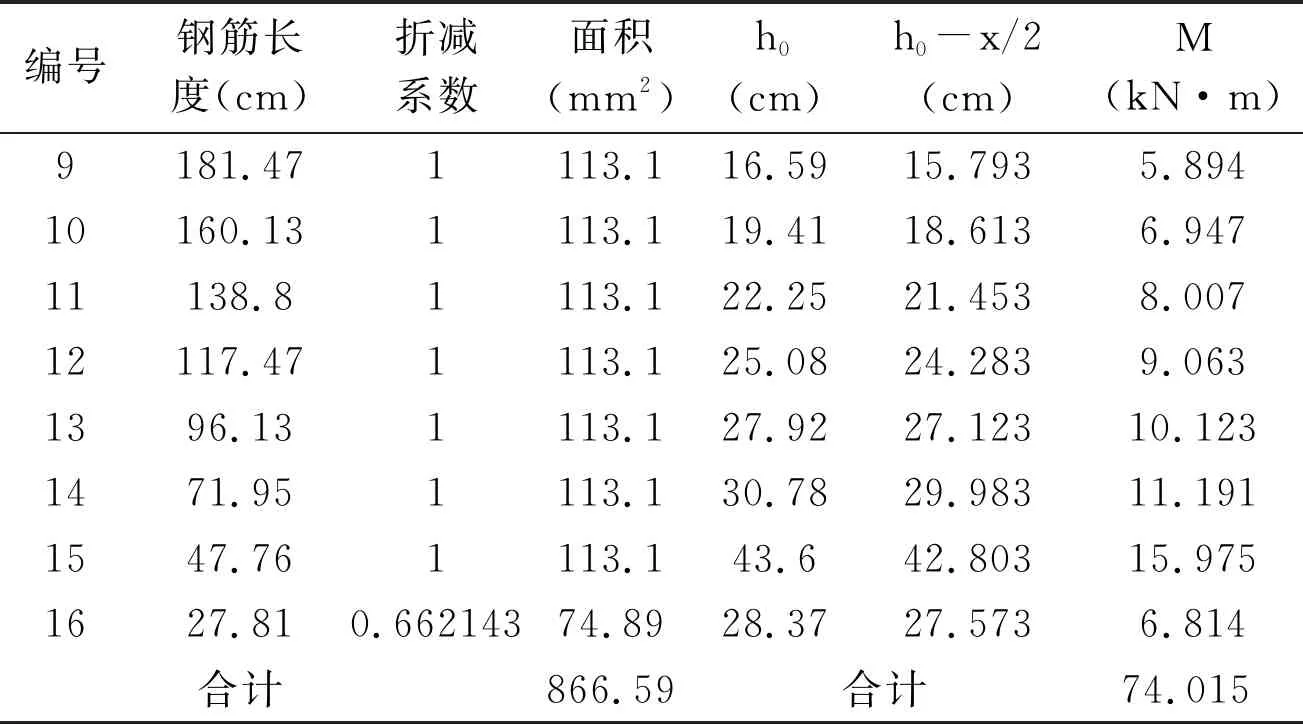
表4 碰撞发生在护栏端部或伸缩缝处Mw计算表
(2)Mc计算
假定2.6m的屈服线范围内考虑24根箍筋的抗弯承载力,即每延米9.23根箍筋。由于端部箍筋的配筋与标准段一致,因此考虑将标准段的Mc值进行一定的折减即为端部的Mc值,折减系数为9.23/10=0.923。因此Mc=140×0.923=129.24kN·m/m。
(3)护栏抗力Rw计算
对于无横梁的钢筋混凝土,Mb=0。SS级护栏屈服线长度Lt=2.4m,将上述Mw、Mc分别带入式(3)、式(4)计算破坏的临界长度和护栏对横向荷载的抗力标准值分别为:
经计算,横向碰撞发生在护栏端部或伸缩缝处的屈服临界长度为2.67m,与Mw计算时假定的临界长度2.6m相差不多,Mw的计算基本符合实际。护栏端部和伸缩缝处满足抗横向碰撞的要求。
3 结语
梳理了基于屈服线理论的混凝土护栏设计原理、设计流程、设计示例,得到的主要结论如下:
(1)按照屈服线设计理念,针对护栏横向碰撞承载能力验算,结合中美规范提出了相应的设计流程和方法,为混凝土护栏设计和安全性能评价提供了依据。
(2)基于屈服线理论的混凝土护栏设计,充分结合了车-护栏动力学反应、塑性变形理论、能量守恒定理等,推导出护栏发生碰撞破坏的临界长度和横向荷载抗力标准值。相比于传统的强度设计理念,该方法与护栏实际碰撞模式相符程度更高,计算更为准确。
(3)按照屈服线理论,护栏与桥梁悬臂板的设计是相辅相成的(由于篇幅有限,本文不详述)。护栏设计的前提假定是桥面板的破坏模式发生在护栏范围内,并不延伸至桥面板。因此桥面板的设计应保证桥面板的屈服滞后于护栏,护栏设计也应避免因过度设计导致桥面板过度设计。
