真三轴状态下盘形滚刀破岩特性

史越，傅鹤林，张加兵，胡才超，刘运思，邓皇适

（1. 中南大学 土木工程学院，湖南 长沙 410075；2. 湖南科技大学 土木工程学院，湖南 湘潭411201）

近年来，随着我国城市轨道交通、山岭隧道、地下管线等深部岩体工程的兴起，隧道自动化掘进装备得到了飞速发展和广泛应用.盘形滚刀是隧道掘进机破岩的核心部件，在不同的应力状态、设计形式和贯入度等条件下，会表现出不同的工作特性.开挖面岩体是一种复杂地质体，随着埋深的增大和地应力场的变化，其力学特性和破坏模式等通常也会出现显著变化.因此，真实考虑开挖面岩体的受荷状态，准确计算开挖过程中岩体破碎情况和滚刀受力变化，具有重要的理论价值和工程指导意义.

在岩体强度计算理论方面，传统的Mohr-Coulomb 等单轴或一般三轴模型无法合理描述中主应力对岩体力学性质或行为的影响，难以解释深部岩体现场所表现的变形或破坏现象，而Drucker-Prager 准则[1]解释了静水压力对岩石材料屈服与破坏的影响，表述了真三轴状态下岩土体的应力路径，且计算效率较高、收敛性好，近年来已在岩土工程计算中得到了逐步应用和完善：Alejano 等[2]、邓楚键等[3]通过M-C 准则与D-P 系列准则的匹配关系，提出了D-P 系列准则的应用条件、相互关系和转换方法；许文松等[4]基于M-C 准则和D-P 系列准则的匹配关系，探讨了粘聚力、内摩擦角和Lode 参数在围岩稳定分析中的折减规律和衰减路径；何川等[5]采用D-P 屈服准则对渗流影响下的圆形隧道围岩进行弹塑性分析，并结合现场实测和数值计算结果进行了对比验证. 在滚刀破岩力的理论计算与模拟分析方面，破岩过程中的刀岩接触关系和仿真模型精度始终是该方向的研究重点：Yang 等[6]建立了考虑岩体脆性损伤、刀盘运动轨迹和切削磨损的有限元分析模型，提出了一种侧向力非对称理论模型；Choi 等[7]、杨圣奇等[8]、刘学伟等[9]、谭青等[10]等提出了含结构面岩体的切削力计算方法，建立了滚刀破岩离散元模型；Labra 等[11]将离散元和有限元分别应用在被切削岩石样品断裂损伤和未损伤的两个子域中，提出了滚刀破岩过程中的离散-有限元混合模型，并与室内试验结果进行了对比验证；夏毅敏等[12-13]和张桂菊等[14]基于M-C 理论和数值计算结果，得到了不同围压和温度条件下的岩石破碎特征和滚刀荷载特性.

在实际工程中，滚刀破岩类似于多轴状态下的加载破碎，各向应力的相对大小往往比等围压工况更具研究意义.本文借助表征中主应力效应的系数β[15]，将CSM（Colorado School of Mines）常截面滚刀模型中的切削单元体置于三轴应力状态下，建立了基于D-P 准则的滚刀破岩理论模型和仿真模型，在验证模型可靠性的基础上，研究真三轴状态对滚刀破岩特性的影响规律，从而为盾构机掘进参数设置、刀盘设计优化和刀具选型配置等问题提供理论和技术参考.

1 基本理论

1.1 Drucker-Prager 强度理论

Drucker 和Prager[1]取压应力为正，拉应力为负，在π 平面用一簇光滑圆曲线逼近M-C 准则，提出了Drucker-Prager 准则：

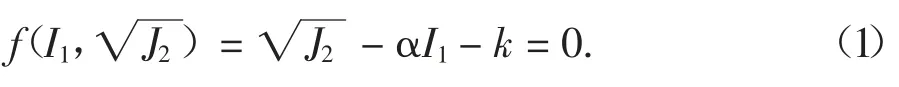
式中：I1为第一应力不变量；J2为第二应力偏量不变量；α，k 为对应不同形式D-P 准则的试验常数，一般与岩石的内摩擦角和内聚力有关.

为研究受荷岩体各向围压的相对大小，定义中主应力系数β 为：

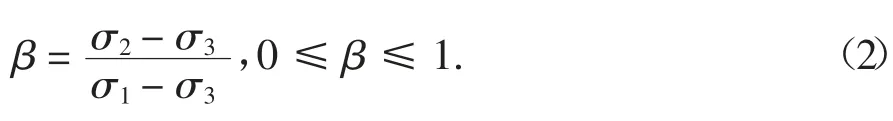
式中：σ1、σ2、σ3分别为岩体所受大、中、小3 个主应力的量值，MPa.

D-P 准则在真三轴极限条件下（三轴拉伸，σ1＝σ2≥σ3），与M-C 外角点外接圆（DP1）匹配；在一般三轴条件下（三轴压缩，σ1≥σ2＝σ3），与M-C 内角点外接圆（DP2）匹配[2-3]，π 平面屈服线如图1 所示，此时α 和k 的表达式为：

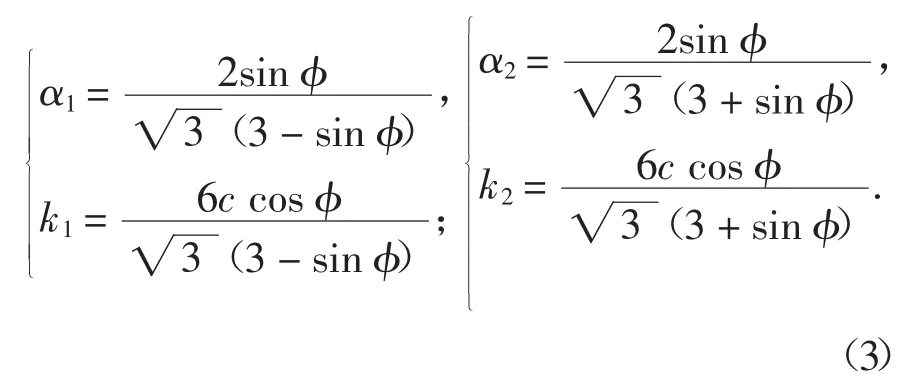
结合式（1）（3），式（2）可表示为：

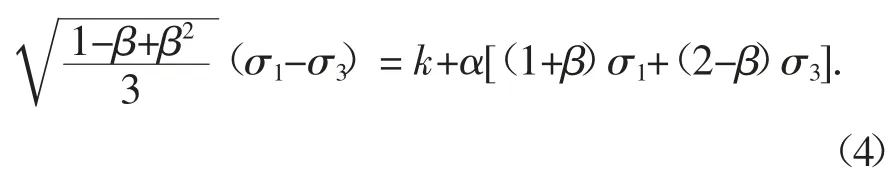
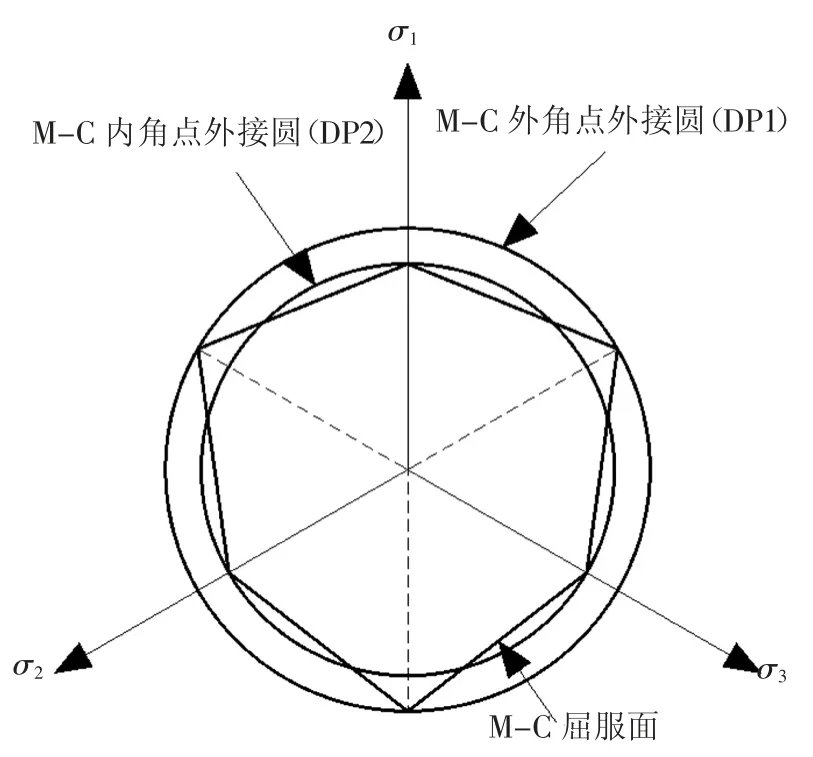
图1 π 平面上M-C 准则与D-P 准则的关系Fig.1 Relationship between M-C and D-P criterion on π plane

根据文献[15]中的计算结果，Dunham 白云岩（φ=35°、c=78 MPa）在σ3=25 MPa 的情况下，D-P 准则两匹配圆（DP1 和DP2）的强度变化情况如图2 所示.可以看出，真三轴极限状态（DP1）比一般三轴状态（DP2）的岩石计算强度增大很多，反映出中间主应力对岩石强度变化有较为明显的影响，这是单轴或一般三轴强度理论无法表达的.

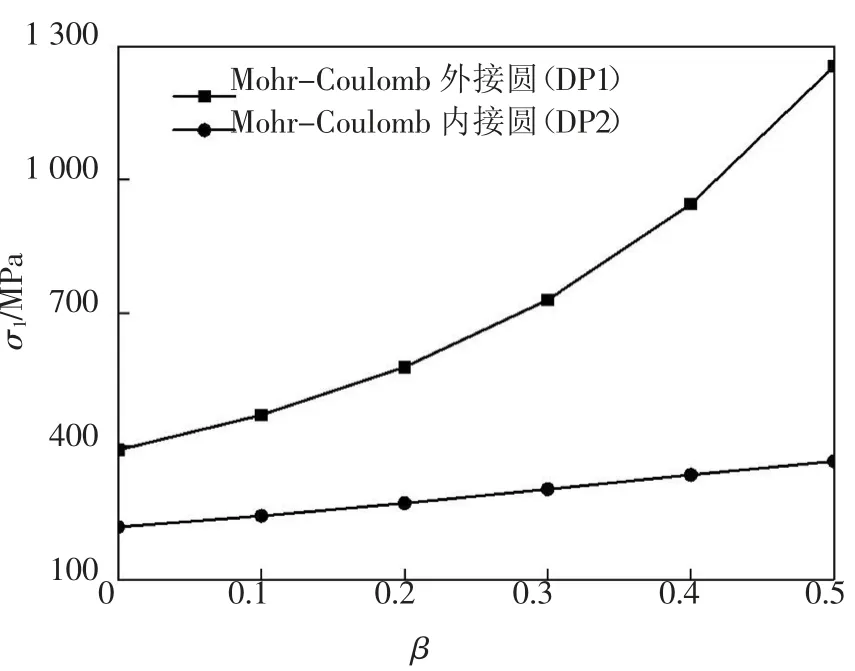
图2 DP1 和DP2 的关系Fig.2 Relationship between DP1 and DP2

1.2 滚刀-岩体作用模型

基于室内线性切割试验结果，Rostami 等[16]提出了CSM 常截面滚刀破岩接触模型.该模型认为，滚刀与岩石间的滚动摩擦力远小于径向压力而作纯滚动运动；掘进方向上的围岩抗力是滚刀破岩时所受的主要阻力；滚刀在切割岩石时接触面上的压力近似均匀分布；岩石受滚刀碾压作用而破碎，其在受压状态下主要发生剪切破坏.但该模型并未考虑被切削岩体在不同围压下的强度变化，计算结果难以表征深部应力场的强度特性，因此，可在刀岩接触面上任取一个岩石单元进行三轴应力状态分析，σ1为滚刀破岩应力，σ2和σ3为单元体侧面围压，如图3 所示.

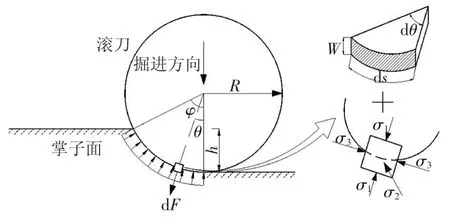
图3 滚刀下的应力分布及分析单元受力状态图Fig.3 Stress distribution under the hob and stress state of an analysis element

盘形滚刀在破岩过程中的三向受力情况如图4所示.沿刀岩接触弧面对分析单元积分，可得到滚刀受力的近似计算式：

式中：Fr为切向滚动力，kN；Fn为法向垂直力，kN；W为刀刃宽度，mm；R 为滚刀半径，mm；θ 为刀岩接触方向与竖直方向的夹角；φ 为刀岩接触面弧度；ψ 为刀尖压力分布系数，取0.1；p0为Rostami 通过实验和回归分析得到的滚刀正下方基准压力计算值[15]：

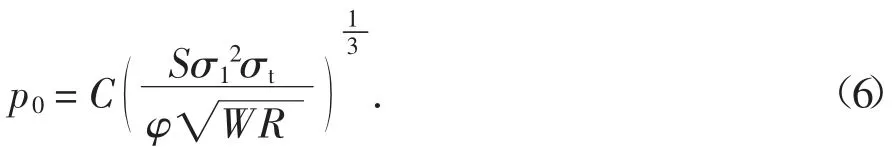
式中：σ1为岩石抗压强度，MPa；σt为岩石抗拉强度，MPa；S 为刀刃间距，mm.令h 为滚刀贯入度，由图3可得几何关系：

由于贯入度h 远小于滚刀半径R，所以φ≈sinφ，（2R-h）≈2R，则

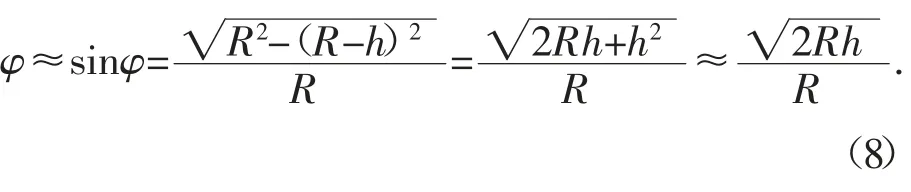
又因为

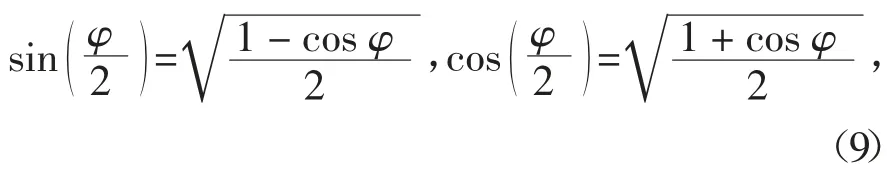
且岩土类材料抗压强度σ1为抗拉强度σt的8～12倍，取σt=0.1σ1，可得：

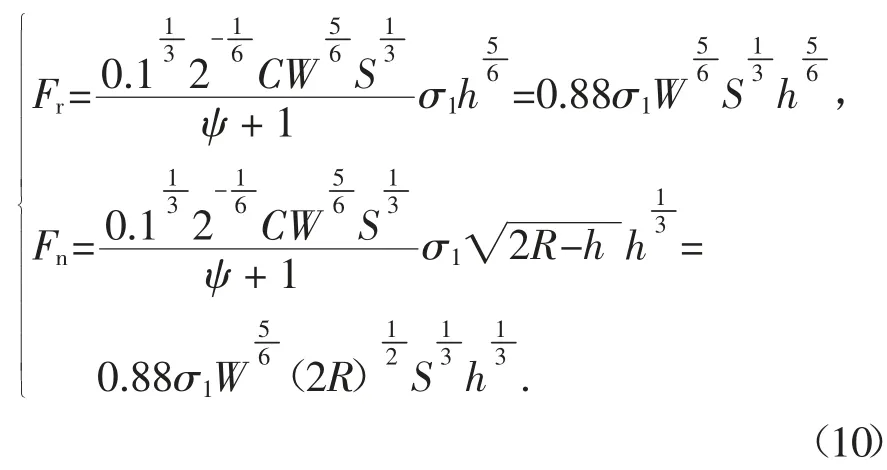
将式（10）与式（4）组合，可得到真三轴状态下基于D-P 准则的盘形滚刀破岩力计算模型.

图4 盘形滚刀受力分析Fig.4 Force analysis of a disc cutter

1.3 掘进总推力计算模型

掘进总推力F 主要包括：盘形滚刀破碎掌子面岩层的推力F1；盾体克服围岩摩擦阻力的推力F2；刀盘稳定掌子面侧向压力的推力F3；掘进机后配套设备牵引力F4；克服盾尾与管片间摩擦阻力的推力F5；曲线掘进时克服变向阻力的推力F6.因F1～F3约占总推力的90%～95%[17]，所以对F4～F6的影响，本文忽略不计，则隧道掘进机总推力计算式为：

盾构刀盘上虽然交错排列着数十把不同类型的刀具，同一时刻不同位置的滚刀还有自转和公转两个自由度，运动轨迹和受力情况各不相同，但从统计角度分析盾构掘进过程中刀盘的受力时，可认为破岩行为由盘形滚刀来完成且其平均受力近似相等[18]，F1可近似表示为：

式中：N 为刀盘上安装的滚刀数（忽略中心刀、面刀和边刀的区别）.借鉴Rostami 等[16]的滚刀破岩推力计算模型，F2的计算式为：

其中

式中：D 为盾构机外径，m；L 为盾构主机长度，m；fs为地层与盾壳之间的摩擦因数；G 为刀盘质量，t；k为岩体侧压力系数；p1为盾构机上部压力，kN/m2；p2为盾构机底部压力，kN/m2；p3为盾构机上部侧压力，kN/m2；p4为盾构机底部侧压力，kN/m2；γ 为岩体的重力密度，kN/m3.F3计算式为：

其中

式中：Pd为刀盘轴线处侧向压力，kN/m2；k0为岩体压力系数.

2 算例分析

长株潭城际铁路某盾构区间全长4.3 km，断面直径为9.34 m，管片外径为9 m，内径为8.1 m，洞顶埋深为6～49 m.地质勘探报告显示，洞顶埋深42～49 m 范围内主要揭露岩层为含砾砂岩层，开挖面岩体强度较高、整体性良好、地质构造形迹不明显，对刀具的磨损较为严重，如图5 所示.在此工况下，准确计算单把滚刀破岩过程中的受荷情况、优化刀具配置就显得十分必要.

图5 盘形滚刀的破岩损耗Fig.5 Partial grinding of a disc hob in tunneling

在隧道开挖的过程中，盾构司机室的监视系统实时采集各类掘进参数，主要包括总推力、贯入度、土舱压力、注浆压力、刀盘转速、刀盘扭矩、刀盘出口压力、螺旋输送机转速、各组推进油缸压力和行程等.选取埋深45 ～49 m 范围内十环做典型断面，掘进参数见表1，破岩力反算参数见表2.

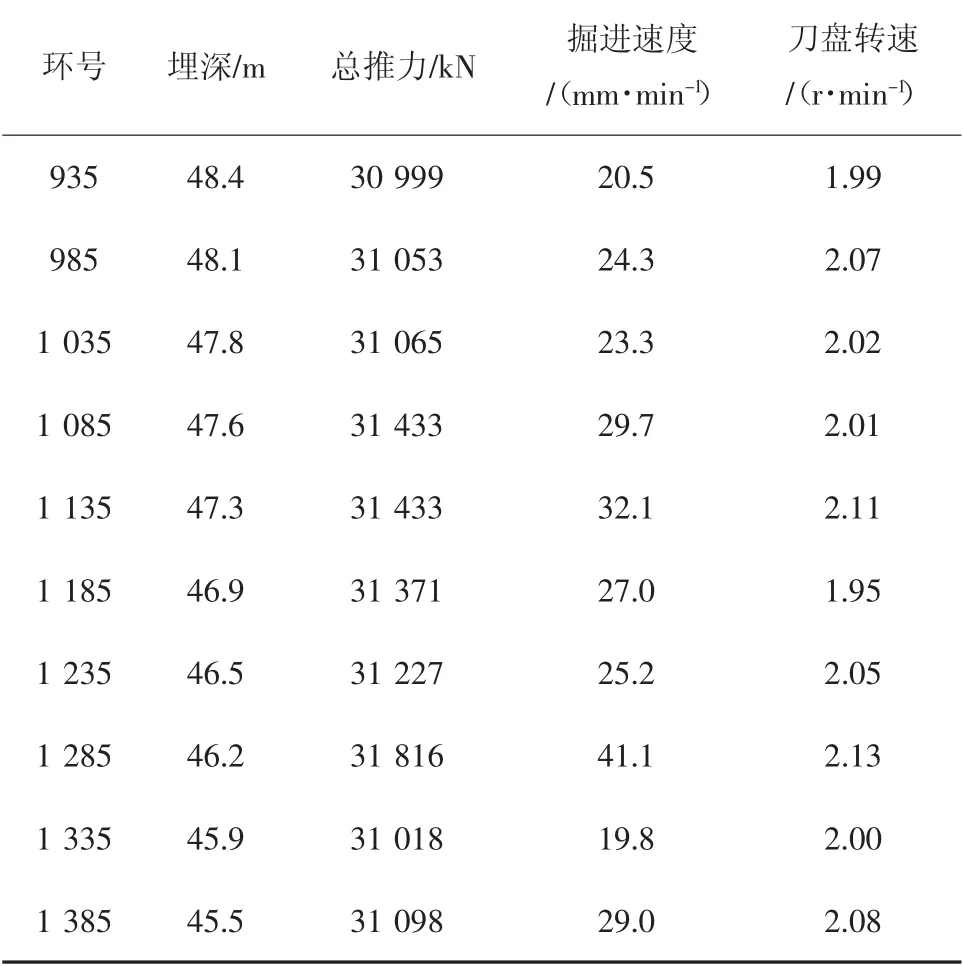
表1 典型断面掘进参数Tab.1 Driving parameters of typical section

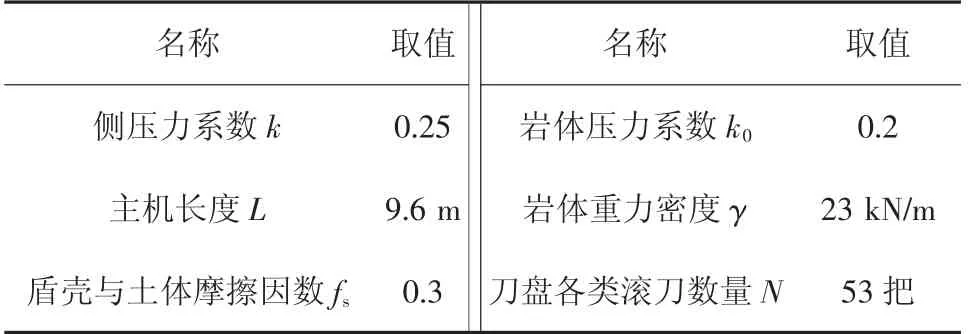
表2 典型断面破岩力反算参数Tab.2 Back calculation parameters of rock breaking force for typical sections

根据式（11）～（16）和典型断面掘进参数（见表1），对滚刀破岩力进行反算，盾体克服围岩摩擦阻力的推力F2为23 505 kN，刀盘稳定掌子面侧向压力的推力F3为1 839 kN，盘形滚刀破碎掌子面岩层的推力F1和单把滚刀法向垂直力Fn的计算结果如表3所示.

由于盾构区间含砾砂岩层埋深在42～49 m 范围内，结合地质勘探情况和室内压缩试验可知，10 个典型断面的地层压力变化不大且中主应力系数β 在0.02 左右，因此，取β=0.02 代入式（4），得到典型断面岩体强度σ1，将真三轴强度代入式（10）便可得到单把滚刀破岩垂直力的理论值，并与表3 中的总推力实测反算值进行对比，如图6 所示.实测掘进总推力的大小主要与滚刀法向垂直力有关，而与切向滚动力的关系不明显，所以无法对比滚动力的情况.

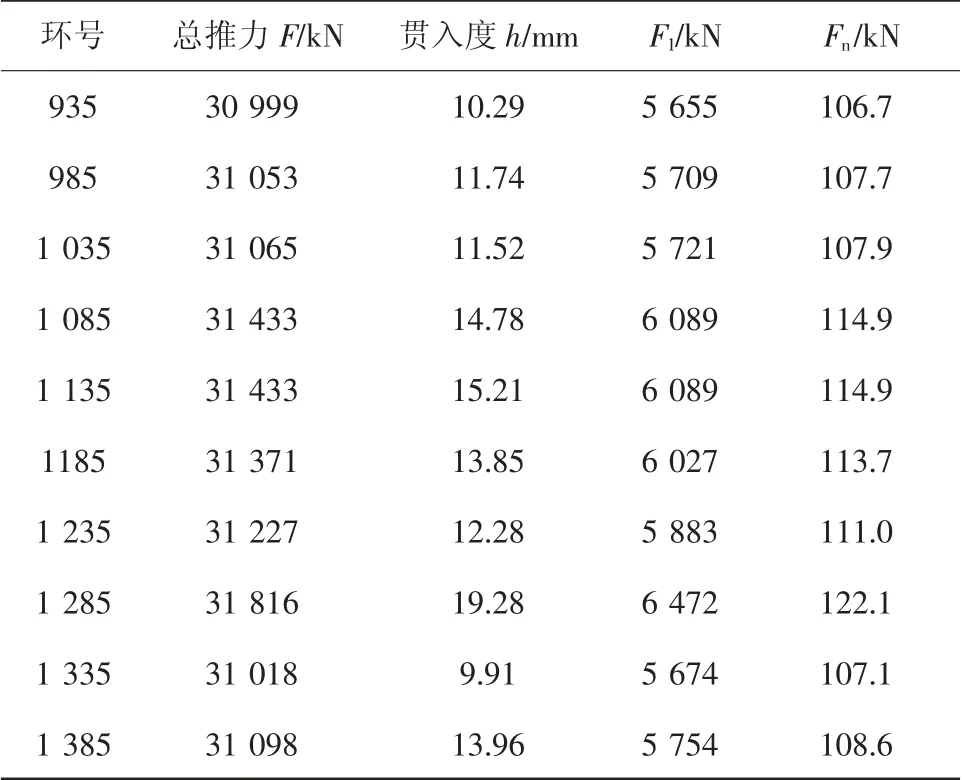
表3 典型断面单把滚刀破岩力计算表Tab.3 The rock breaking force of a hob for typical sections

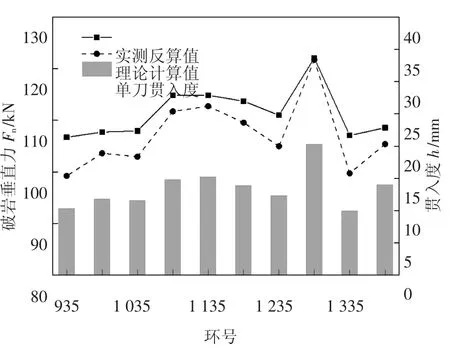
图6 典型断面单刀破岩垂直力实测值和理论值对比Fig.6 Comparison of measured values and calculated values of vertical forces for a single hob cutter in typical sections

由图6 可知，典型断面盘形滚刀破岩垂直力的实测值和理论值变化趋势基本一致，最大相对误差为7.5%，在一定程度上验证了本文所提模型的正确性和准确性；实测反算值均略大于理论计算值，这主要是由于本文中的总推力模型忽略了F4～F6的影响，也反映出F4～F6在总推力中所占的比例较小，可以适当简化；在典型断面各向应力基本相同的情况下，贯入度越大理论值与实测值越接近，这是由于贯入深度较大时岩体的损伤程度增加，降低了后续破岩所需的推力.

3 建立仿真模型

在当前工程技术条件下，中主应力系数β 的取值一般很小，而在深部岩体工程中进行数据采集又较为困难，因此，仿真分析软件为高地应力场盘形滚刀受力和岩石破碎情况研究提供了良好条件.盘形滚刀各部件较为复杂，本文忽略刀轴、刀毂等部分，将其简化为刀圈来研究，滚刀破岩计算模型如图7 所示.模型中岩石材料参数见表4，滚刀刀圈材料参数见表5，且设定岩石部件服从D-P 强度理论和剪切失效准则.

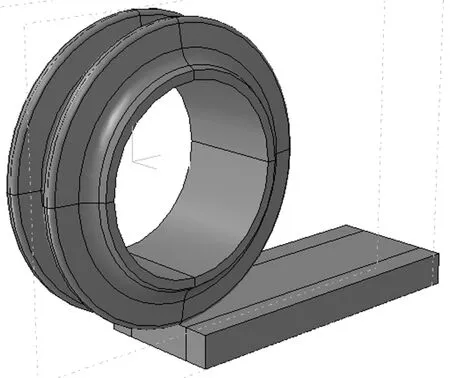
图7 盘形滚刀破岩数值计算模型Fig.7 Numerical calculation model of rock breaking process

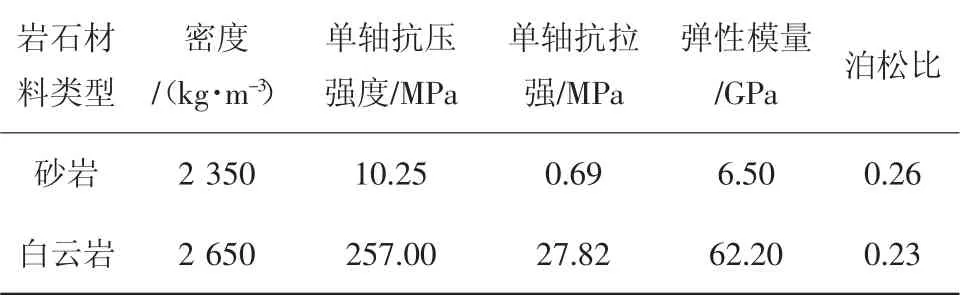
表4 岩石材料参数Tab.4 Material parameter of sandtone

表5 盘形滚刀刀圈参数Tab.5 Cutter ring parameters of disc hob

计算前在滚刀中心建立参考点，并将其与刀圈表面耦合，岩石底面施加全约束，岩石切削面不施加约束，刀岩接触关系为面-面接触、运动接触法、有限滑移，设置不同的岩石侧面初始均布载荷σ2、σ3和刀盘贯入度h，计算工况如表6 所示.其中，工况1 为典型断面现场实测数据，工况2～8 为MOGI 对Dunham白云岩的真三轴压缩试验结果[19].

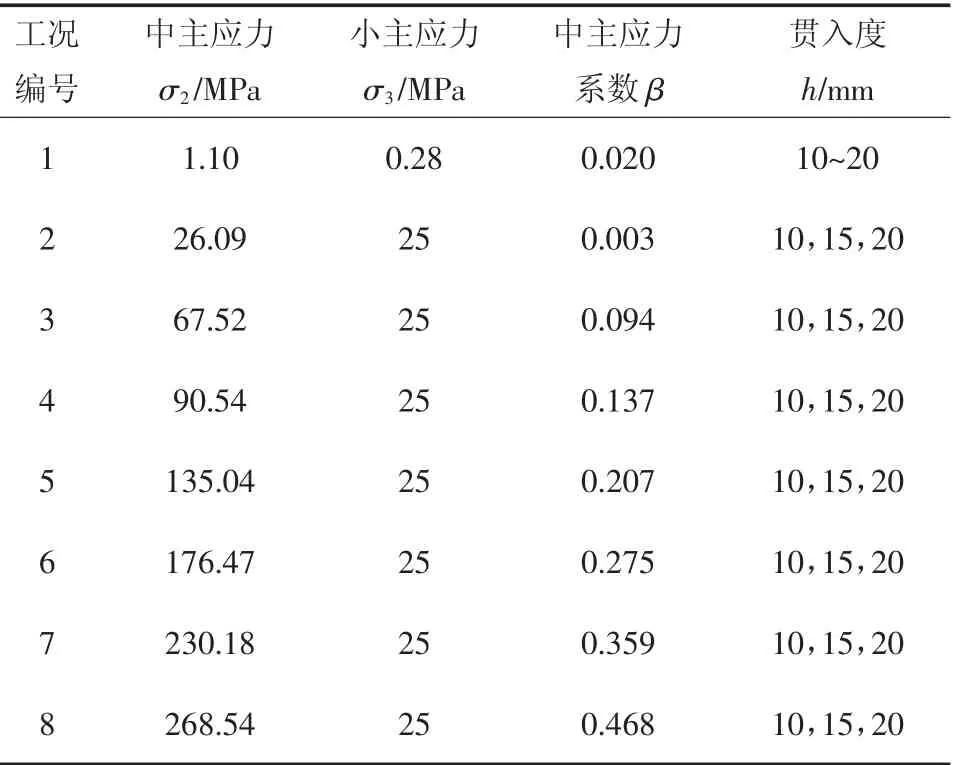
表6 模型计算工况Tab.6 Calculation condition of model

在盾构机破岩掘进的过程中，油缸顶进和刀盘转动两个工序循环配合进行，因此，各工况设置为剪切破岩和滚压破岩两个分析步（如图8 所示）：1）滚刀垂直岩石表面下切达到指定贯入度，设置与贯入度相应的下切速度v1，时间历程0.05 s；2）滚刀以近似直线轨迹切割岩石部件，速度v2，为使刀岩之间没有相对滑移，还需设置相应自转角速度ω，时间历程根据实际切削速度设置.模拟过程中记录滚刀所受的垂直力、滚动力、侧向力以及岩石的破碎情况.

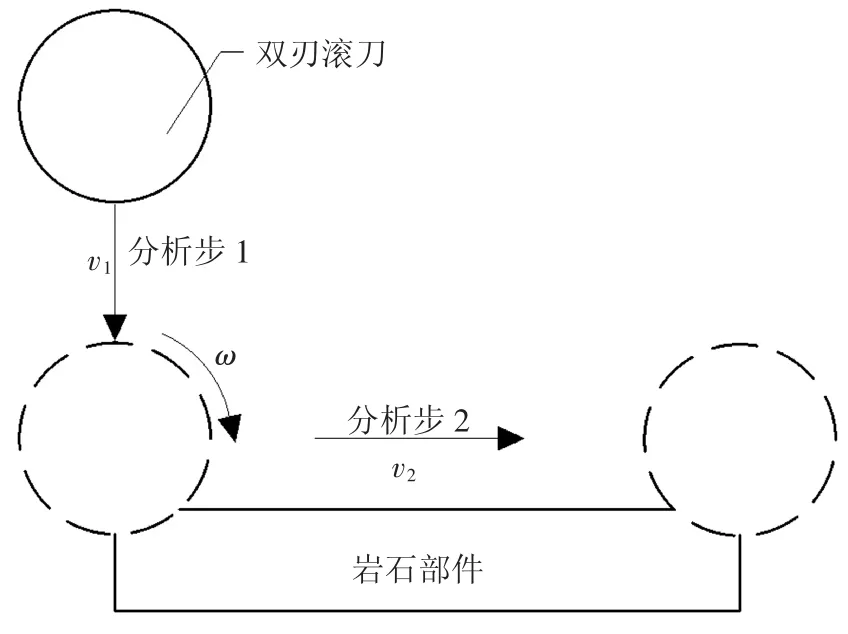
图8 滚刀破岩模型分析步示意图Fig.8 Analysis step of rock breaking model

4 模拟结果分析

工况1 条件下滚刀破岩垂直力和滚动力的实测反算值、理论计算值和仿真值如图9 所示.可知：仿真结果与实测值和计算值的变化趋势相同，垂直力最大相对误差为11.4%，证明了所建仿真模型的可靠性和准确性；仿真结果相对较小且贯入度越大偏差越明显，这主要是由于有限元软件通过单元删除来模拟岩体破碎，当贯入度较大时，破碎单元的大量删除和应力清零使滚刀受荷较小，造成了计算误差.

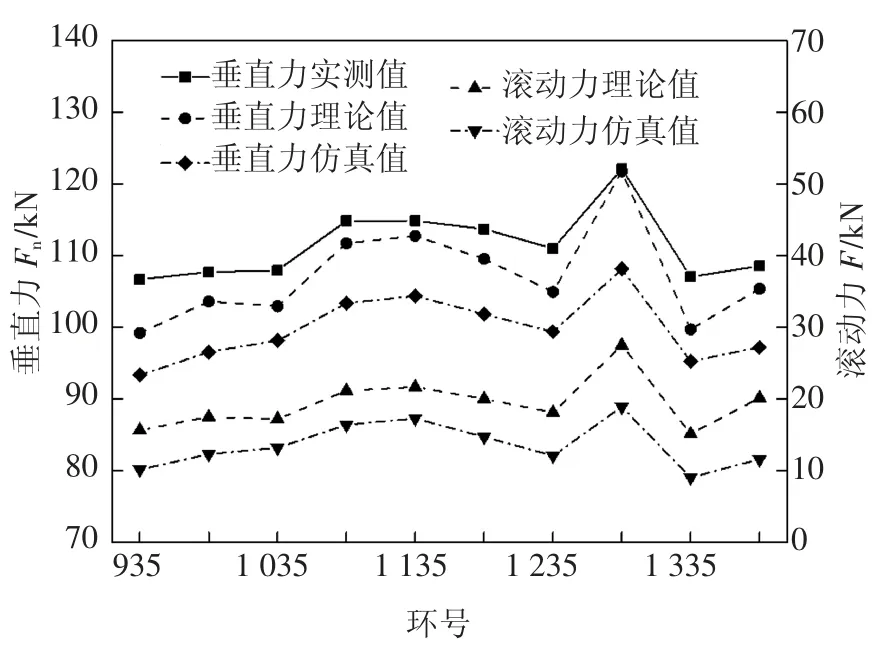
图9 典型断面破岩力实测值、计算值和仿真值对比Fig.9 Comparison of measured values，calculated values and simulation values of rock breaking forces for typical sections

4.1 岩石的破碎特征

各工况计算结果虽有较大不同，但模型的应力云图和破碎特征类似，这里以工况2（h=10 mm）为例进行说明.如图10 所示，可以看出，分析步1 为剪切破岩，刀岩接触点在滚刀正下方，此时接触点受力与刀具相同且瞬时较大；分析步2 为滚压破岩，刀岩接触点为切槽前端面，待切槽贯通后（图10（e）），虽然滚刀尚未离开岩石，但此时岩石所受的大主应力明显减小.

对工况2～8 的破岩单元数量进行统计并绘制其变化曲线，如图11 所示，分析可知，贯入度相同时，随着中主应力系数的增加，破岩单元数量呈指数型减少，20 mm 贯入度下β=0.468 较β=0.003 时减少了50.2%，这是由于中主应力作用增大了岩石强度，造成了刀岩接触面附近的岩石单元难以达到屈服，破碎困难；中主应力效应相同时，随着贯入度的增加，破岩单元数量明显增加，中主应力系数β=0.003时，h=20 mm 较h=10 mm 增加了2.1 倍，这是由于贯入度越大，对岩石的扰动和损伤就越大，且贯入的刀尖宽度增大，造成了破碎单元数量的增加.

图10 盘形滚刀破岩过程中的大主应力云图（工况2，h=10 mm）Fig.10 Major principal stress cloud chart of disc hob in rock breaking process（condition 2，h=10 mm）

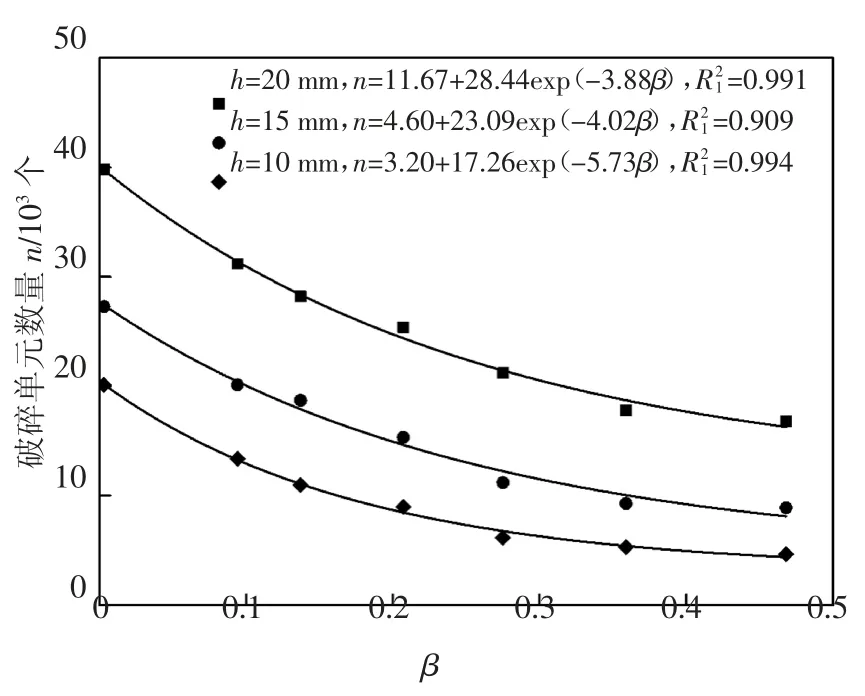
图11 岩石破碎单元数量与中主应力系数的关系Fig.11 Relationship between the number of rock breaking units and coefficient of intermediate principal stress

4.2 破岩力变化特征

数值计算得到的滚刀各向力时程曲线是瞬时波动力，由计算结果可知，工况2～8 的波动趋势基本类似，其波动极值反映了各工况的载荷特性，这里以工况2（h=10 mm）为例进行说明.如图12 所示，可以看出，随着刀岩接触面岩体塑性应变的增大，各破岩力迅速增大，岩体破碎瞬间又迅速下降，此过程反复发生从而完成破岩；滚刀剪切破岩所受的垂直力明显大于滚压破岩阶段，两阶段极值相比达到了2.2倍，这主要是由于剪切破岩须使岩石部件形成“切槽”，滚压破岩时只需沿该槽继续前进，从而降低了滚压破岩期间滚刀垂直方向所受的载荷；滚动力、侧向力的时程变化与切削方式的关系不大，在破岩过程中极值没有出现明显的衰减；同时刻滚动力和垂直力的变化趋势基本相同，这也验证了本文式（10）对二者类似表达形式的推导；破岩过程中侧向力始终较小且出现了正负方向的变化，这是因为侧向力是由刀刃两侧的不平衡力相互抵消而产生的，该力会导致滚刀沿轴方向的振动，引起刀刃偏磨，进而影响滚刀寿命.

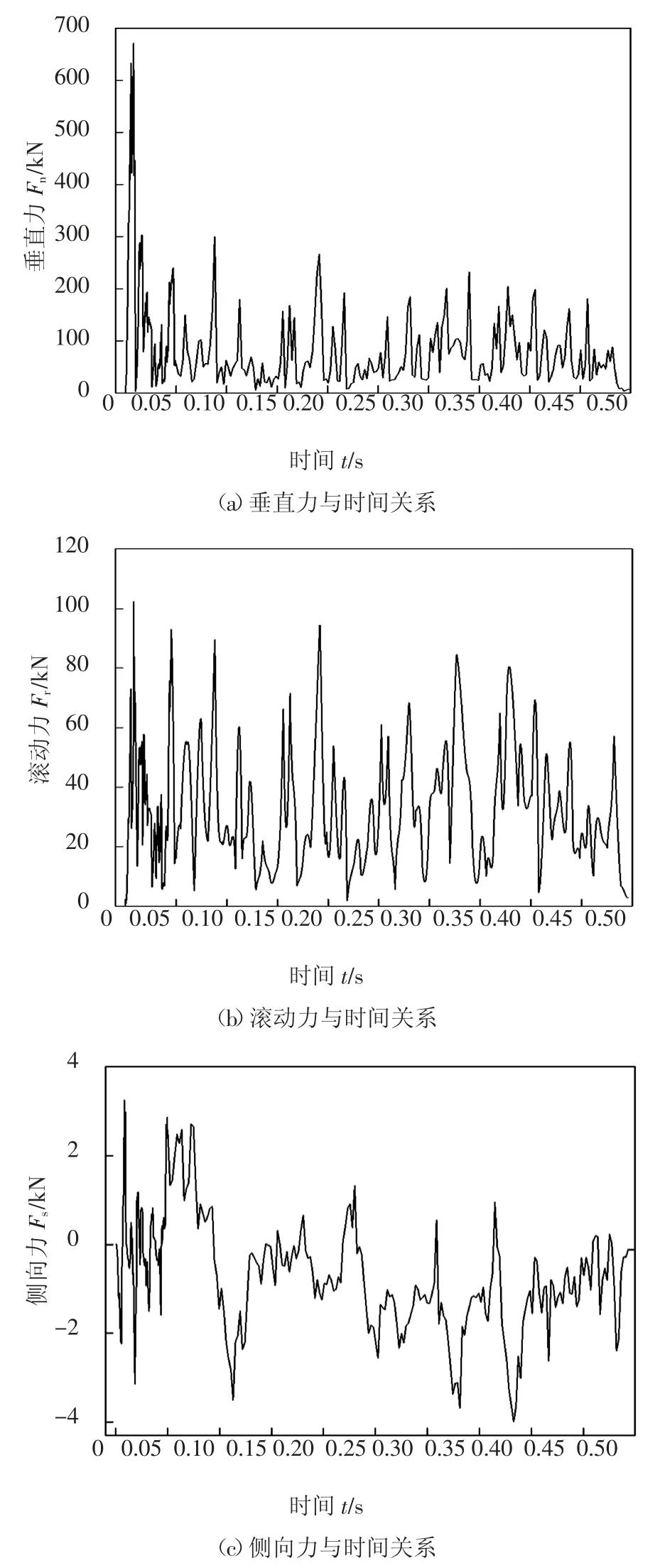
图12 滚刀破岩过程中的破岩力时程曲线（工况2，h=10 mm）Fig.12 Force curve of disc hob during rock breaking process（condition 2，h=10 mm）

从图12 的各向力时程曲线可知，明确不同的应力条件下的滚刀最大载荷对配置刀具和设置掘进参数等都具有重要意义.因此，在不考虑滚刀材料受荷能力的情况下，对工况2～8 的最大破岩力进行计算并绘制其变化曲线，如图13 所示.分析可知，贯入度相同时，随着中主应力系数的增加，破岩最大垂直力、滚动力和侧向力均呈指数型增加，20 mm 贯入度下β=0.003 时的最大垂直力、滚动力和侧向力分别为β=0.468 时的33%、34%和47%，说明随着中主应力效应的增强，岩石强度得到了提高，需要更大的破岩力才能使之破碎，由于侧向力反映的是刀刃两侧的压力差，所以增幅相对较小；由回归曲线可知，β=0.468 时h=20 mm 与h=10 mm 相比垂直力、滚动力和侧向力分别为1.6 倍、1.7 倍和2.1 倍，且随着贯入度的增大，垂直力、滚动力和侧向力曲线的斜率均增加，其中侧向力的增幅最大，表明滚刀与岩石接触面积越大，刀具的载荷效应越强，受力增加越显著.滚刀各向受力的增加显著降低了滚刀的使用寿命，因此，对于高地应力场工程应采取增大滚刀直径、增加多刃滚刀配置数量和及时开舱换刀等措施，以保证滚刀的破岩效率.

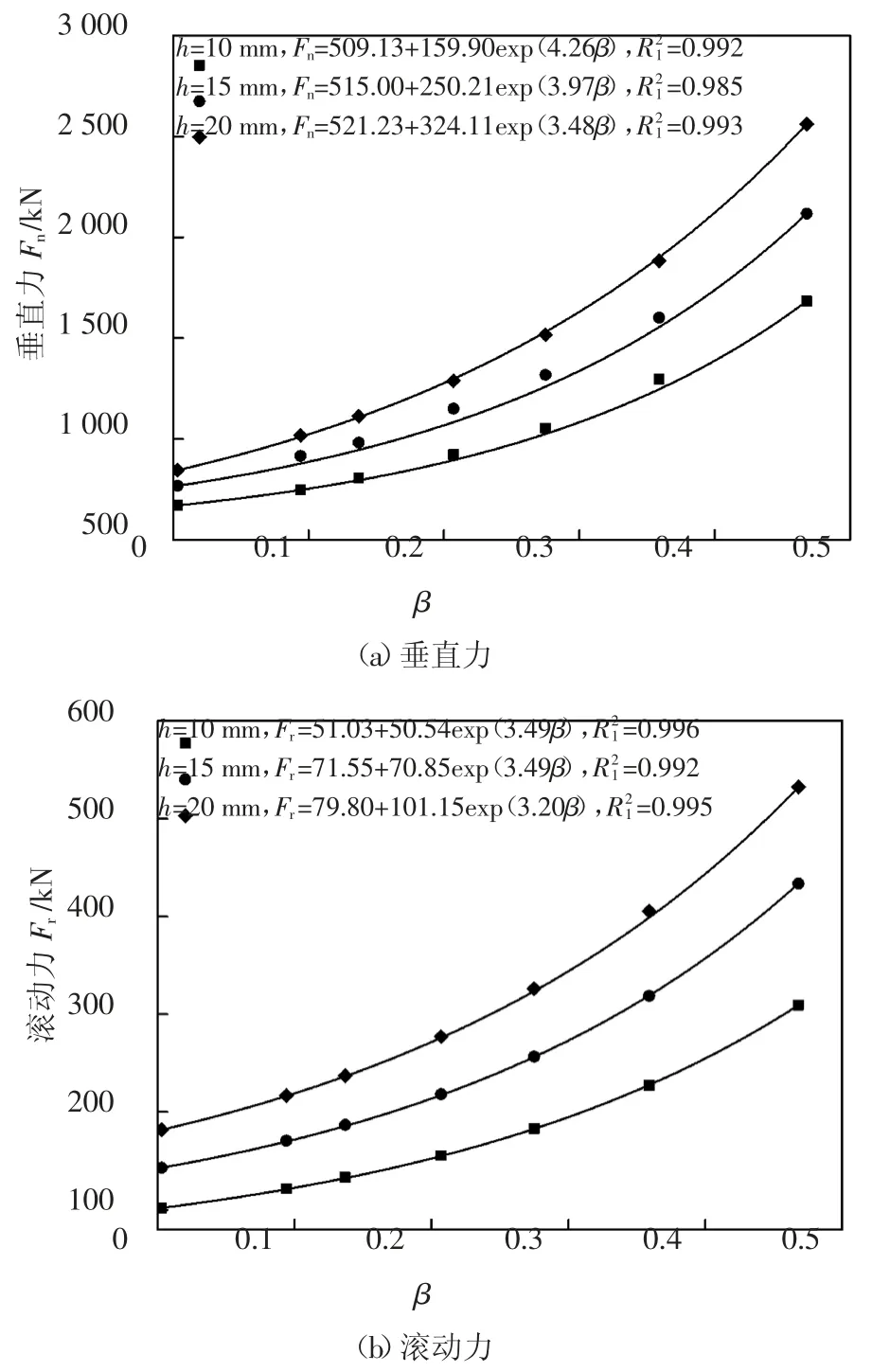
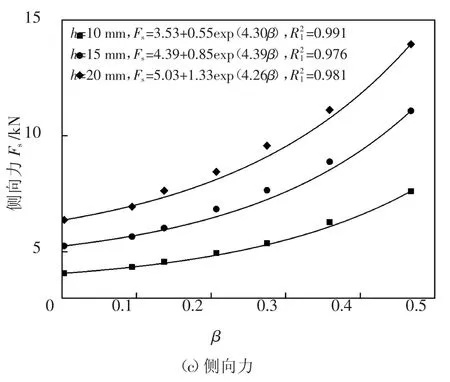
图13 最大破岩力与中主应力系数的关系Fig.13 Relationship between the maximum rock breaking force and coefficient of intermediate principal stress

5 结 论

针对高地应力场隧道掘进机盘形滚刀的载荷问题，提出基于Drucker-Prager 强度准则和CSM 修正模型的滚刀受力计算方法，根据真三轴状态下三向应力的相对大小，探讨中间主应力的作用效应，主要结论如下：

1）π 平面上Mohr-Coulomb 屈服面的外接圆和内接圆构成了岩石真三轴极限状态和一般三轴状态的强度包络线，其差值是由中主应力的作用引起的，且影响显著，这是单轴或一般三轴强度模型所无法表达的.

2）将CSM 滚刀-岩石接触模型中的岩石单元修正为真三轴状态，结合Drucker-Prager 强度准则建立三向应力条件下滚刀破岩载荷模型；根据隧道掘进机的工作原理和滚刀载荷理论模型，将滚刀破岩划分为剪切破岩和滚压破岩两个过程，建立滚刀破岩仿真模型，将现场实测反算值、理论计算值和仿真结果对比，验证了理论模型和仿真模型的可靠性和准确性.

3）剪切破岩阶段垂直力极值明显大于滚压阶段，两阶段极值相比达到2.2 倍，而滚动力和侧向力始终在理论范围内波动，与破岩模式的关系不大，侧向力较小但方向不断变化，造成了刀具的振动与偏磨，降低了刀具的使用寿命.

4）贯入度相同时，随着中主应力效应的增强，破碎单元数量呈指数型减少，最大垂直力、滚动力和侧向力均呈指数型增加，其中侧向力的增幅相对较小；相同中主应力条件下，随着贯入度的增大，破碎单元数量和三向破岩力均增大，且各向破岩力的增加也越来越显著，其中侧向力的增幅相对较大.

5）滚刀各向受力的增加显著降低了滚刀的使用寿命，因此，对于高地应力场工程应采取增大滚刀直径、增加多刃滚刀配置数量和及时开舱换刀等措施，以保证滚刀的破岩效率.