网格式框架的等效抗侧刚度分析

吴琴，张华刚†，李富江，张鑫，魏艳辉，马克俭，2

（1. 贵州大学 空间结构研究中心，贵州 贵阳550003；2. 湖南大学 土木工程学院，湖南 长沙410082；3. 贵州建工监理咨询有限公司，贵州 贵阳550081）

我国的磷矿资源较为丰富，对湿法生产磷酸后排放的磷石膏进行资源化利用，是综合治理磷石膏污染的有效途径.鉴于当前对磷石膏应用的领域主要集中在化工、建材、农业和矿山回填等这一现状[1-2]，马克俭等[3]提出现浇磷石膏-混凝土网格式框架组合墙结构，可将磷石膏作为承重材料现浇应用于建筑结构中；张华刚、吴琴等[4-5]系统测定了现浇磷石膏的抗压强度和本构关系，并在小高层结构中成功进行了组合墙的工程实践[6]；卢亚琴等[7]开展了低周往复水平荷载作用下的缩尺模型试验，表明这种组合墙破坏时主要表现为剪切型破坏，这是因为网格式框架是在普通框架基础上增设了中间柱和层间梁，从而形成密柱密梁框架，并使框架和现浇磷石膏互为有效约束的缘故.姜忻良等[8-9]对混凝土密排内框架-纤维石膏板组合墙所做的低周往复荷载试验表明，内框架仅在层高处设混凝土梁连接密排芯柱，因此结构破坏时密排芯柱表现为弯曲型破坏，结构的受力性能类似于带竖缝的剪力墙，可见设置层间梁将改变结构的受力性质.

现浇磷石膏具有高度脆性性质[4]，在将组合墙应用于高层建筑而现浇磷石膏又开裂后，混凝土网格式框架将成为结构的主要承重骨架[7]，而网格式框架的面外刚度又相对较弱.张华刚等[10]对其开展了稳定承载力研究，获得了弹性临界力的解析解.在组合墙自身平面内，网格式框架的抗侧刚度将成为影响结构抗侧性能的关键因素，王其明等[11]、刘阳等[12]主要基于有限元分析，讨论了梁柱线刚度比值等因素对抗侧刚度的影响.上述研究工作对推动这种组合墙的工程应用是有益的.

水平荷载对高层建筑的影响往往起控制作用，设计时需经过多轮计算才能合理确定结构的承载力.在现浇磷石膏-混凝土网格式框架组合墙中，地震作用下现浇磷石膏可作为结构抵抗水平荷载的安全储备，因此有必要提供网格式框架抗侧刚度的等效计算公式，以便预估结构的抗侧能力，提高结构设计效率.本文基于D 值法，综合考虑剪切变形和弯曲变形的影响来推导网格式框架的等效抗侧刚度，并采用有限元法和试验结果加以验证，以期为结构的工程应用提供参考.

1 网格式框架的等效抗侧刚度

1.1 结构的剪切刚度

如图1 所示，由D 值法可得网格式框架第j 列第i 行柱的抗侧刚度为[13]：

式中：αij为梁柱线刚度比值对柱剪切刚度的影响系数；hci为结构第i 行网格的高度；icij为柱的线刚度.则结构第i 行网格的抗侧刚度为：

式中：2n 为结构的柱总数.水平荷载作用下结构第i行网格的侧移为：

则其剪切变形为：

式中：Vi为结构第i 行网格的总剪力.当γi=1 时，可得其剪切刚度为：

可见，当梁柱的线刚度改变时，网格式框架的剪切刚度随即会变，为简化计算，可采用加权平均值来表征其剪切刚度：

式中：H 为结构总高度；m 为结构的竖向网格数.

图1 计算简图Fig.1 Calculation diagram

1.2 结构的侧移计算

1.2.1 侧移计算原理

将结构整体看作悬臂立柱，则水平荷载引起的侧移将由弯曲侧移和剪切侧移叠加而成，其中弯曲侧移由柱的拉伸和压缩引起，剪切侧移由梁柱自身的弯曲变形引起，均可由虚功原理计算[14].

在图1 上从某行网格的柱中点截断结构后，水平荷载引起的结构总弯矩M（x）将由柱轴力合成的弯矩来平衡，如图2 所示.假设柱的轴力在水平截面上按线性分布，则第j 列柱的轴力Nj（x）与边柱轴力Nb（x）的关系见式（7）.

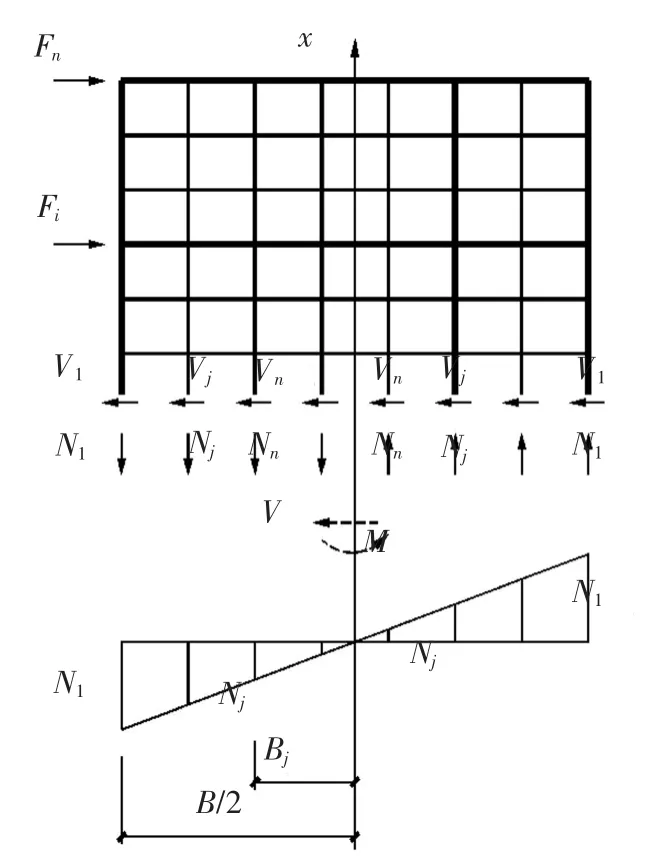
图2 结构内力平衡Fig.2 Structural internal force balance

式中：B 为网格式框架的宽度；Bj为第j 列柱与x 轴的距离，则由力矩平衡关系可得边柱的轴力为：

式中：n 为网格式框架B/2 宽度内的柱数，因此结构的弯曲侧移可按式（9）计算.

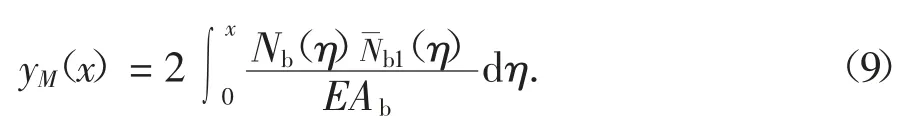
式中：N（bη）为结构在η 高度处由荷载引起的边柱轴力η）为在x 高度处施加单位水平力后引起η 高度处的边柱轴力；EAb为单侧边柱的轴向刚度，近似采用加权平均值表示：

剪切变形引起的侧移按虚功原理为：

叠加式（9）、式（11）得网格式框架的总侧移为：

1.2.2 结构侧移计算

1）倒三角形分布荷载作用

在倒三角形分布荷载q 作用下，由式（8）可得网格式框架的边柱在任意高度x 处的轴力为：

其中M0=qH2/3，为倒三角形分布荷载作用下结构的柱脚总弯矩.在结构x 高度处施加单位水平集中力后，边柱在结构高度η 处的轴力为：

引入相对坐标ξ=x/H 后，由式（9）可得结构的弯曲侧移为：

由式（11）可得结构的剪切侧移为：

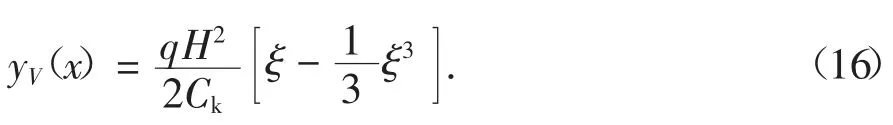
当ξ=1 时，由式（12）可得结构的顶点侧移为：

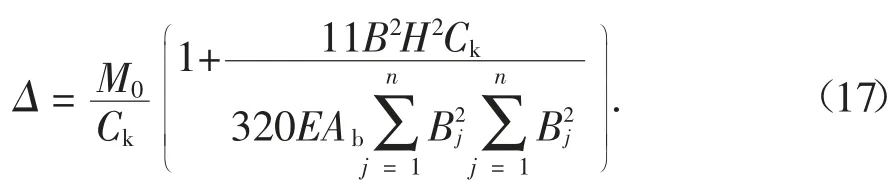
2）顶点集中荷载作用

在顶点水平集中荷载F 作用下，由式（8）可得结构边柱的轴力为：

在高度x 处施加单位水平集中力后，引起边柱在结构高度η 处的轴力为：

则由式（9）和式（11）可分别得结构的弯曲侧移和剪切侧移为：

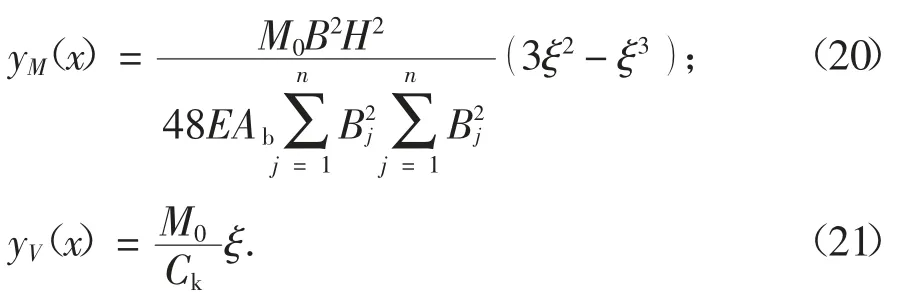
其中M0=FH，为顶点集中力引起的柱脚总弯矩.同样由式（12）可得结构的顶点侧移为：

3）均布荷载作用

由式（8）可得到均布荷载q 作用下结构边柱轴力为：

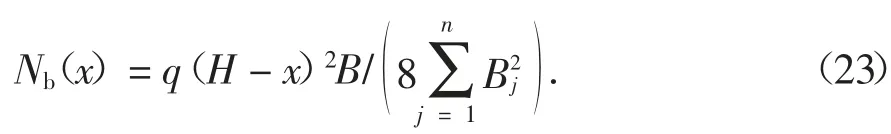
在结构高度x 处施加的单位水平力引起结构高度η 处的边柱轴力为：

因此由式（9）和式（11）分别得结构的弯曲侧移和剪切侧移为：

其中M0=qH2/2，为均布荷载引起的结构柱脚总弯矩.则由式（12）可得结构的顶点侧移为：

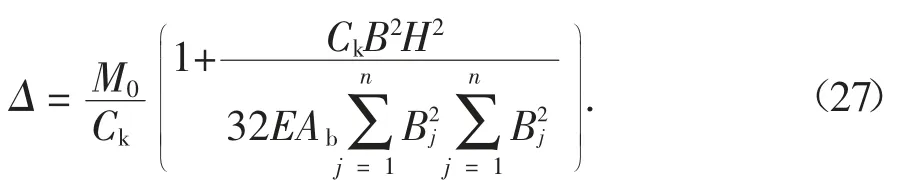
1.3 结构的等效抗侧刚度

比拟荷载作用下悬臂梁的位移计算，可由式（17）、式（22）和式（27）得到网格式框架的等效抗侧刚度，并统一表述为：

式中：β 为计算系数，倒三角形分布荷载作用时取为1/3.64，顶点集中荷载作用时取1/3，均布荷载作用时取1/4；γ 为柱轴向变形的影响系数，按以下公式计算.

1）倒三角形分布荷载作用

2）顶点集中荷载作用

3）均布荷载作用

当不计中柱轴向变形对弯曲侧移的影响时，γ 可简化为：

1）倒三角形分布荷载作用

2 有限元验证

此处基于有限元基本原理来验证前述式（28）的计算精度.算例情况如图3 所示，混凝土的强度等级为C30.

图3 算例简图Fig.3 Example diagram

按前节理论，由式（6）计算网格式框架加权剪切刚度的过程见表1，结构等效抗侧刚度及顶点位移的计算结果详见表2，其中弯曲侧移和剪切侧移分别按式（9）和式（11）计算.结构顶点位移计算所用的荷载值分别为：1）倒三角形分布荷载作用时，q=225 kN/m；2）顶点集中力作用时，F=100 kN；3）均布荷载作用时，q=250 kN/m.

有限元分析时，由于楼层梁和层间梁的跨度较小而有可能成为深梁，采用普通梁单元将不能估计梁的剪切变形影响，故全部结构构件均采用了8 节点弹性块体单元[15]，柱脚节点均约束其三向线位移以模拟嵌固支承，有限元模型如图4 所示.混凝土的弹性模量Ec=3×104N/mm2，泊松比ν=0.2，忽略钢筋的影响，分别施加前述3 种荷载进行计算，顶点位移的结果详见表2，表中还给出了按顶点位移折算的结构抗侧刚度.

理论计算结果表明，中柱的拉伸和压缩变形对结构等效抗侧刚度和顶点侧移的影响几乎可忽略.在本算例的顶点总侧移中，剪切侧移的占比在98%左右，因此结构在水平荷载作用下以剪切变形为主.与有限元结果相比，本算例在前述3 种荷载作用下，理论计算的结构等效抗侧刚度约小于有限元计算结果折算抗侧刚度的5.0%～10.0%，倒三角形分布荷载的理论侧移值与有限元结果的误差均值为5.62%，均布荷载误差均值为9.745%，顶部集中荷载的误差均值为9.062%.可见式（28）的计算精度较为理想，且可不计中柱的拉伸和压缩变形对结构等效抗侧刚度的影响.

表1 结构的加权剪切刚度计算Tab.1 Weighted shearing stiffness calculation of the structure

表2 结构等效抗侧刚度及位移计算Tab.2 Equivalent lateral stiffness and displacement calculation of the structure

图4 有限元模型Fig.4 Finite element model

3 试验验证

3.1 试验概况

试验数据来源于现浇磷石膏-混凝土网格式框架组合墙低周往复荷载试验的对比结构，相关试验结果将另文介绍，此处以3 榀网格式框架在混凝土开裂前的试验结果来验证等效抗侧刚度计算公式的精度.

试件情况如图5 所示，试件编号为KJQ-1、KJQ-2、KJQ-3，结构厚度均为50 mm.混凝土的实测弹性模量为25 463 N/mm2，立方体抗压强度标准值为20.09 N/mm2.试验加载装置如图6 所示，在试件顶部采用50 t 的千斤顶施加有水平可滑动的竖向荷载，并保持恒定，水平荷载通过25 t 的MTS 作动器以位移控制、并往复施加在结构顶部的梁轴上.

图7 所示为混凝土开裂前在水平荷载为1 kN时3 个试件的楼层梁水平位移测试结果，图8 所示为试件在单调加载时的顶点荷载-位移曲线.可见3个试件在相同水平荷载作用下的侧移结果较为接近，且近似呈线性关系.

图5 网格式框架试件Fig.5 Grid frame structure specimen

图6 试验装置Fig.6 Test equipment

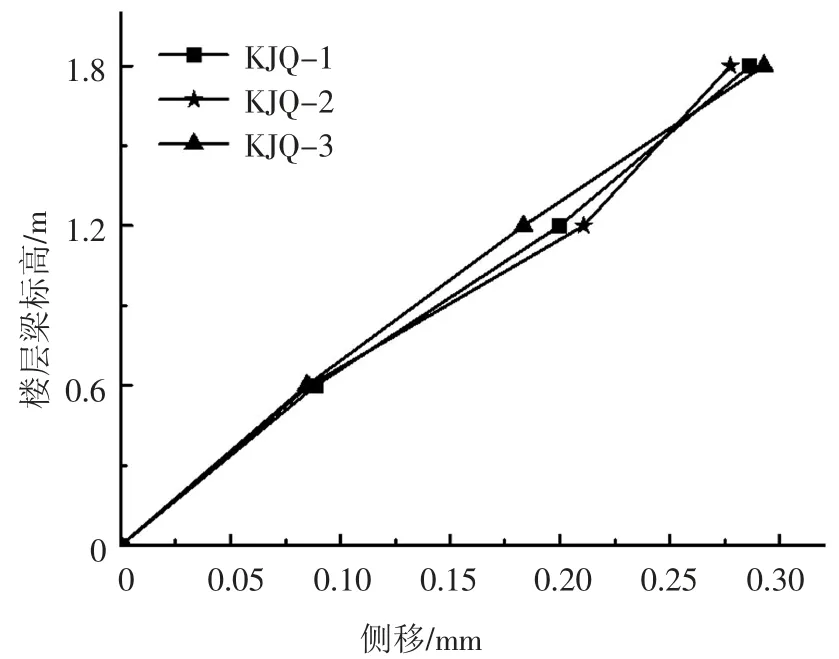
图7 楼层梁水平位移测试结果Fig.7 Horizontal displacement test results of floor beam

图8 单调加载的荷载-位移曲线Fig.8 Load-displacement curves of monotonic loading

3.2 计算结果验证

表3 给出了有限元计算的位移结果及3 个试件楼层梁位移的平均测试值，测试结果与有限元计算结果较为接近.

根据前节分析，不计中柱轴向变形对弯曲侧移的影响，按式（20）和式（21）计算的理论侧移值与试验值相比，最大侧移约大10.5%；当不计弯曲变形时，最大侧移约小10.6%.理论侧移值与有限元计算的结果相比，当考虑弯曲侧移时，最大侧移约大14.5%；当不计弯曲侧移时，最大侧移约小14.8%，这是与前节算例的不同之处，因为从表3 可看出，结构高度的增加将使弯曲侧移在总侧移中的占比增大，故结构侧移计算应考虑弯曲变形的影响.

表3 结构侧移结果的验证Tab.3 Verification of structural lateral displacement results

不计中柱的拉伸和压缩变形影响，按式（28）计算的等效抗侧刚度见表4，大体与有限元方法折算的抗侧刚度相当，但与试件折算的平均抗侧刚度相比，约小8.6%，可见式（28）具有理想的计算精度.

表4 结构等效抗侧刚度的验证Tab.4 Verification of equivalent lateral stiffness of structure

4 结 论

1）本文等效抗侧刚度公式考虑了结构弯曲变形和剪切变形的影响，可用于预估结构抗侧能力.

2）应用本文等效抗侧刚度计算公式时，网格式框架的侧移及等效抗侧刚度计算可不考虑中柱轴向变形的影响.

3）与有限元法及试验结果的折算抗侧刚度相比，本文等效抗侧刚度具有理想的计算精度.

4）在结构总侧移中，本文等效抗侧刚度计算的弯曲变形占比随着结构高度的增加而增加，结构侧移计算应考虑弯曲变形的影响.