陶瓷基复合材料连接结构失效 分析方法

刘宝瑞，侯传涛，赵丽滨，吴建国，高魁垠

（1.北京强度环境研究所 可靠性与环境工程技术重点实验室，北京 100076； 2.北京航空航天大学 宇航学院，北京 100191）

碳纤维增强碳化硅陶瓷基复合材料（Carbon Fiber Reinforced Silicon Carbide, C/SiC）具有耐高温、高比强、高比模、抗烧蚀等一系列优异性能，在新一代高超声速飞行器、天地往返飞行器热结构设计中具有广阔的应用前景[1]。其中机械连接是C/SiC 复合材料结构设计的薄弱部位，在地面热强度考核试验过程中，多次出现结构非正常破坏现象，破坏的起始部位往往位于连接部位。因此，C/SiC 复合材料连接结构的强度分析对于整体结构的完整性评估和优化设计具有十分重要的意义。

随着商用有限元软件的不断更新和进步，以ABAQUS 为代表的商用软件已经能够对复合材料结构进行铺层建模，分析获得单个铺层的受力与破坏情况，具备模拟每个铺层的各向异性、渐进损伤和失效破坏分析的能力，很多学者以此为基础，针对复合材料结构失效行为开展了大量的研究工作。Kilic 和Haj-Ali[2]采用ABAQUS 自定义材料子程序，基于Tsai-Wu 失效准则和Ramberg-Osgood 非线性行为对复合材料螺栓连接和开孔结构的拉伸强度进行了分析。Mccarthy M A 等[3][4]建立了复合材料螺栓连接结构渐进损伤有限元模型，分析了结构产生损伤后的性能以及连接间隙等对结构的力学行为和损伤模式的影响。Schuecker C 和Pettermann H E[5]发展了连续损伤模型，与WWFE 的试验结果进行了对比分析。Hochard C[6]等基于剪切损伤和非线弹性应变演化定律编写了ABAQUS 用户材料子程序，研究了开孔试样的损伤行为和强度特征。Lapczyk I 和Hurtado J A[7]基于渐进损伤模型对铝合金/复合材料三明治开孔结 构的拉伸强度进行了仿真分析。Zhang Z[8]等建立了加筋板结构有限元模型，基于改进Hashin 准则研究加筋板的破坏行为。Staniszewski J[9]建立了复合材料层合板的渐进损伤分析程序LAMPATNL，分析了复合材料开孔板的损伤扩展行为。Zhao L 等[10]建立了复合材料螺栓连接结构渐进损伤分析模型，研究了拉伸载荷作用下偏弯效应对连接结构损伤的影响，计算获得的载荷位移规律及失效模式结果与试验数据一致性良好。

以上这些研究方法均未涉及到C/SiC 复合材料机械连接结构的强度与失效分析，且无法同时模拟C/SiC 复合材料的各向异性和非线性特征。文中围绕C/SiC 陶瓷基复合材料连接结构失效分析问题，对几种不同的复合材料失效准则进行了验证与分析。通过分析表明，改进三维Hashin 失效准则应用于C/SiC复合材料结构具有可靠的精度。提出了模量突降和渐进损伤两种分析方法模拟材料的各向异性和非线性特征，针对典型C/SiC 复合材料连接结构进行了失效行为计算，并与试验结果进行了对比分析，验证了两种分析方法的有效性。

1 复合材料结构失效分析方法

1.1 本构模型

文中所研究的C/SiC 复合材料纤维预置体为正交编织的碳纤维布铺层结构，属于典型正交各向异性材料，采用正交各向异性本构模型表征其力学行为，见式（1）。

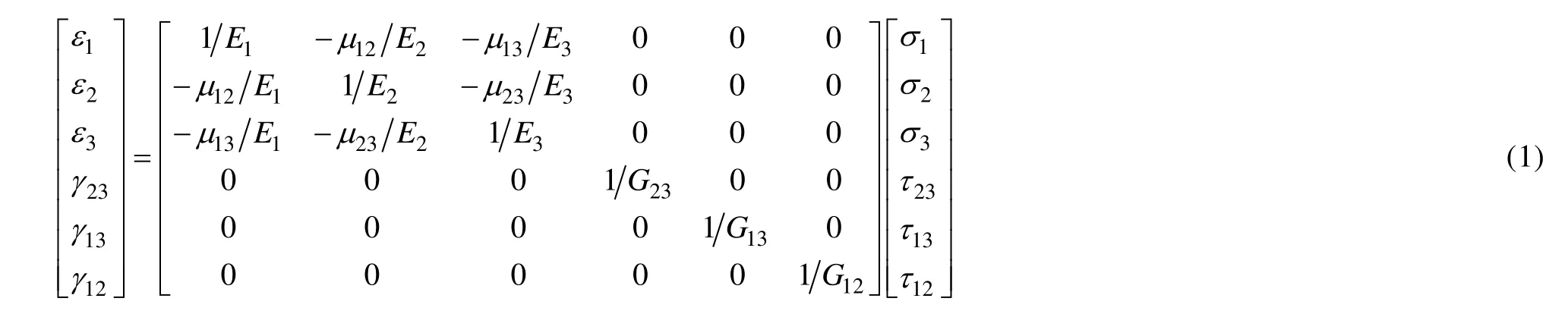
纤维增强陶瓷基复合材料属于非均质材料，包含碳纤维、界面层、基体等复杂组分，制备温度在1000 ℃以上。冷却到室温后，由于各组分的热膨胀系数不同，导致组分间存在热失配，细观结构存在众多微裂纹、孔隙等缺陷。在外界力热载荷作用下，各组分间存在复杂的传力关系，内部细观缺陷也会扩展演化，使得整体复合材料结构呈现出复杂的力学性能非线性特点。文中采用宏观损伤理论来模拟复合材料结构的力学性能非线性特征，并对结构的失效行为进行预测。材料退化方法是宏观损伤理论的重要组成部分，其基本思想是通过降低材料的模量来模拟材料的损伤情况。文中探索了模量突降和渐进损伤两种材料退化方法在复合材料结构力学行为与失效预测中的应用。所用到的材料初始力学参数见表1。

表1 材料力学性能参数Tab.1 Parameters of mechanical performance of materials

1.2 模量突降分析方法

材料模量突降分析模型是当材料发生损伤时，将损伤材料的所有弹性模量乘以一个损伤量d。典型材料模量突降模型的退化因子通常取0。

式中：Ed是损伤后的有效材料模量；E 是未损伤的材料模量。

损伤分析方法中，结构的最终失效判定方法有两种：一种是非收敛准则，该准则定义渐进损伤分析过程中发生不收敛时的最大载荷作为结构的最终失效载荷；另外一种是载荷突降准则，在渐进损伤分析过程中，监视施加位移与总的支反力之间的变化情况，当由于材料失效导致位移载荷增加而支反力明显下降时，模拟终止，最大载荷作为结构失效载荷。

C/SiC 复合材料结构典型的损伤模式包括基体开裂、分层、界面脱粘、纤维断裂等模式，载荷作用方式不同，引起的损伤模式以及导致的材料力学性能下降程度也不一样。文中采用的材料退化模型见表2。其中基体开裂损伤模式的材料模量退化因子根据材料级力学性能和连接结构试验数据确定。

表2 材料退化模型Tab.2 Material degradation model

1.3 渐进损伤分析方法

根据材料力学性能试验数据，采用经验公式拟合的方法获得拉伸、剪切、压缩等典型载荷作用下材料的应力-应变关系，求导获得弹性模量随应变的变化关系[12]。

采用五次多项式函数描述拉伸、剪切的应力应变关系为：

式中：σi为面内主方向应力，MPa；ε 为主方向应变；τ12为面内切应力，MPa；γ12为切应变；εi,tb为拉伸断裂应变；γ12,b为剪切断裂应变；Ai和Bi为拟合系数，由试验曲线拟合得到。对应材料的切线模量见

式（5）和式（6），拟合参数见表3。

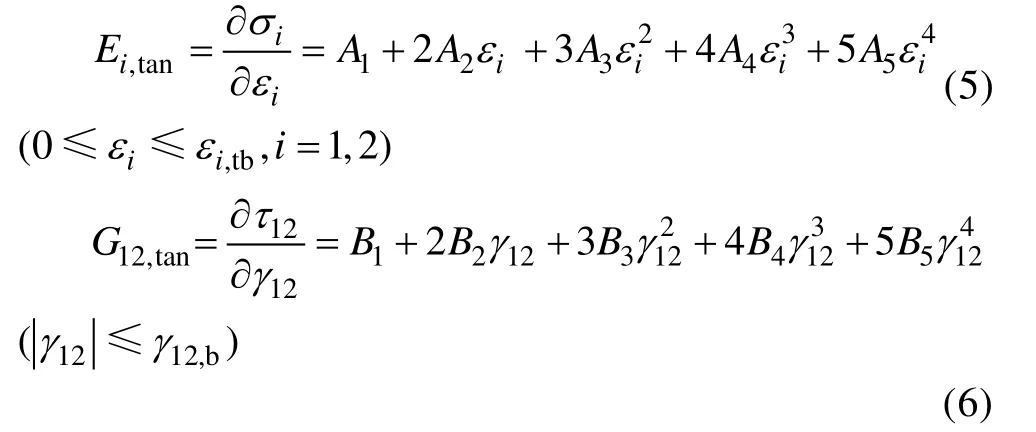
表3 拟合参数Tab.3 Fitting parameters

材料在压缩失效前，应力应变关系近似保持为线弹性，因此假设面内两个方向上的压缩应力应变关系函数为：

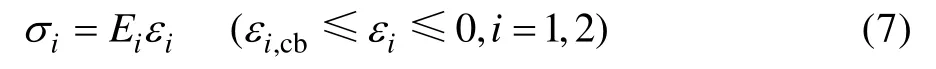
式中：εi,cb为材料主方向上的压缩断裂应变；Ei=105 GPa。

1.4 失效准则

目前，纤维增强复合材料失效准则主要分为以下三类。

1）第一类是唯象失效准则，其特点是忽略复合材料内部具体的损伤模式，在某些典型载荷状态下，能够比较准确地预测复合材料结构的强度破坏值，但是不能解释复合材料的破坏机理。这类强度准则有最大应力准则、最大应变准则、Tsai-Wu 准则等。

2）第二类是“基于机理”的失效准则，可以判断材料的失效模式，如Hashin 准则、Puck 准则等。由于该类准则的触发条件是某种特定的载荷和损伤模式，而实际上结构在受载过程中往往是多种损伤模式互相耦合，准则中损伤模式的假设和损伤演化的时序与理想推论有较大的差距，导致该类准则虽然考虑因素全面，但实际应用中的准确性往往较差。

3）第三类准则是借鉴Tsai-Wu 准则中考虑张量的模型构建方法，在宏观层面上采用多项式展开的方法构建失效准则，典型的有Christensen 失效准则。

针对复合材料结构的失效准则问题，英国的著名复合材料力学专家Hinton 等人发起了WWFE（World Wide Failure Exercise），邀请了世界上纤维增强复合材料破坏理论研究领域的11 个研究组织和知名专家对14 个复合材料破坏理论进行了全面、客观的评估。研究发现，尚没有能够精确预测所有失效模式和所有载荷边界条件的失效准则。也有学者指出，根据不同复合材料的力学性能和载荷特点，对经典的失效准则进行改进和组合使用，在实际应用中往往能够获得较好的结果[14]。

文中在前人研究的基础上，对三维Tsai-Wu、三维Hashin 和Christensen 失效准则在C/SiC 复合材料典型结构失效中的应用效果进行研究。同时根据C/SiC 复合材料非线性、双模量、脆性等力学性能特点，结合最大应力失效准则对Hashin 失效准则进行改进，提出了改进三维Hashin 失效准则。

三维Tsai-Wu 失效准则：

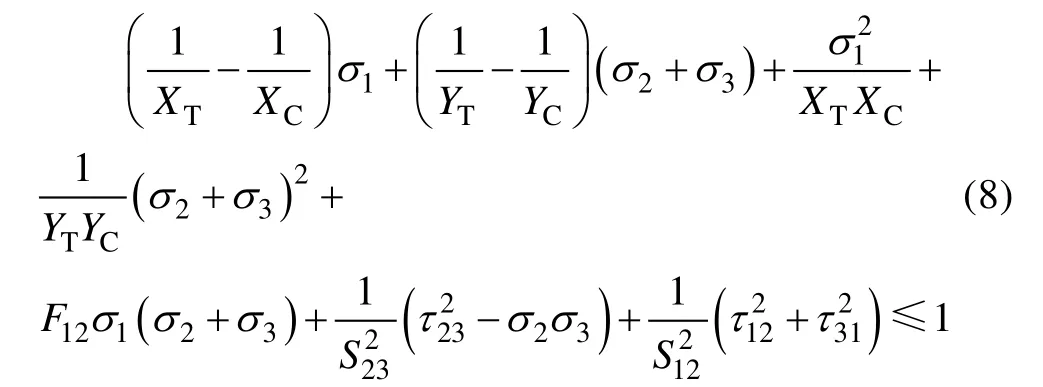
三维Hashin 失效准则：

Christensen 失效准则：

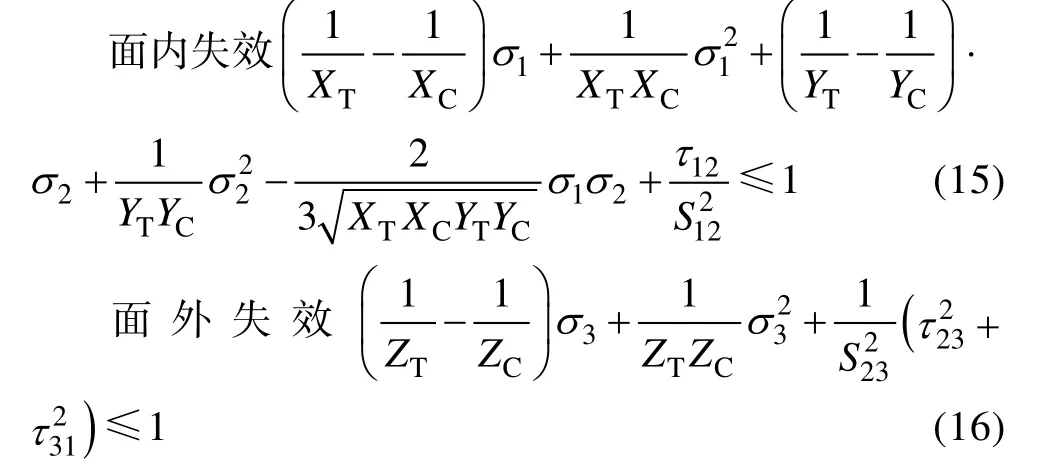
改进三维Hashin 失效准则：

针对文献[15]中的C/SiC 复合材料开孔板拉伸试验，采用渐进损伤分析方法，结合以上四个失效准则开展开孔板的失效分析与对比，结果见表4。可以看出，对于C/SiC 复合材料开孔板，Tsai-Wu 准则和Hashin 准则的失效模式与试验结果一致，但失效载荷明显偏低。Christensen 失效准则的失效载荷与试验结果较为接近，但失效模式误差较大。相比较来看，改进三维Hashin 准则的失效模式与失效载荷与试验结果较为接近。

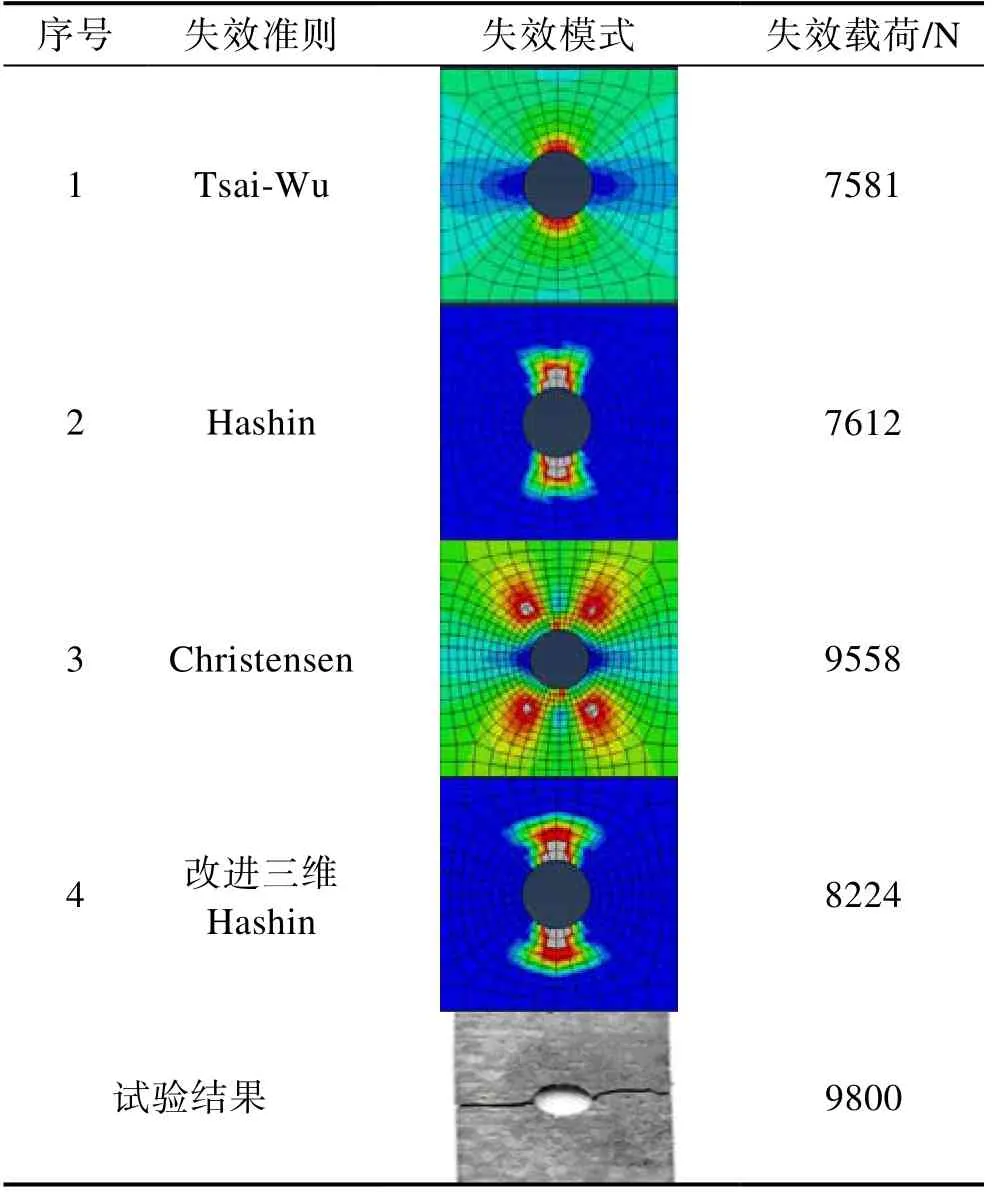
表4 开孔板拉伸失效仿真分析Tab.4 Tensile failure simulation analysis of orifice plate

2 算例分析与验证

分别针对模量突降和渐进损伤两种分析方法，结合改进三维Hashin 失效准则编写Abaqus-Umat 自定义材料有限元分析程序，对典型C/SiC 复合材料试样和C/SiC 连接结构开展失效分析。

2.1 典型复合材料试样拉伸失效分析

采用典型C/SiC 复合材料力学性能试验数据来对两种方法进行验证。建立复合材料试样有限元分析模型（如图1 所示），一端固支，另一端施加拉伸载荷。采用模量突降分析方法和渐进损伤分析方法对该试样拉伸载荷作用下的力学行为进行计算 分析。

图1 C/SiC 复合材料试样模型Fig.1 C/SiC composites sample model

两种方法得到试样的最大主应力分布规律如图2所示。两种方法中间区域最大主应力值相差不大，误差约2.1%。渐进损伤分析方法的应力场分布比较合理，与理论分析一致。模量突降分析方法在试验件的一端存在局部应力畸变现象。

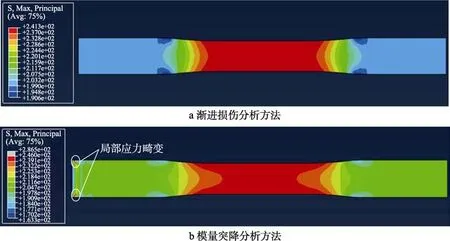
图2 拉伸载荷作用下C/SiC 复合材料试样最大主应力分布Fig.2 C/SiC composites under tensile load sample maximum principal stress distribution: a) progressive damage analysis method; b) modulus plunged by analysis method

提取中间段等应力区域，分析拉伸过程应力-应变关系，结果如图3 所示。渐进损伤分析方法由于模型来源于试验数据，因此和试验结果吻合良好。模量突降法在160 MPa 以下的中低应力区具有较高的计算精度，但在超过160 MPa 的高应力区误差较大。

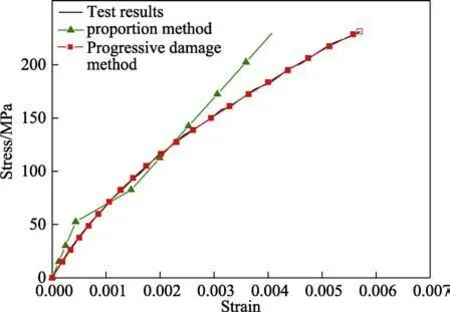
图3 拉伸过程C/SiC 试样应力-应变关系Fig.3 Stress-strain relationship of C/SiC sample during tensile process

2.2 典型复合材料连接结构拉伸失效分析

针对某C/SiC 三钉螺栓连接结构开展强度建模分析。采用C3D8I 单元建立的结构有限元模型如图4所示。螺栓采用实际尺寸建模，为了减少接触对，螺母与螺栓建立为一个整体，螺栓属性与搭接板一致。一个螺栓建立4 个接触对，模型中除了螺栓与搭接板接触之外，搭接板之间也存在一个接触对，模型中总共13 个接触对。接触对法向求解通过直接约束法，切向关系通过库伦摩擦模拟，摩擦系数为0.5。所有部件采用结构化网格，为得到较精确的应力分析结果，对孔边进行网格细化，并对钉孔建立辐射化网格。计算过程中在截面D 上施加固支约束，在截面A 上施加位移载荷，同时由于在试验中夹具限制了搭接板的面外弯曲，在截面B、C 上施加了只允许纵向位移的约束，模型中预紧力施加在螺栓横截面上。

结构一端固支，另一端施加位移载荷。计算获得结构最大主应力场分布如图5 所示。两种方法计算获得的应力场分布规律类似，最大应力位置相同，但渐 进损伤分析方法计算的应力分布云图更加均匀，不同应力水平的过渡更加平滑。

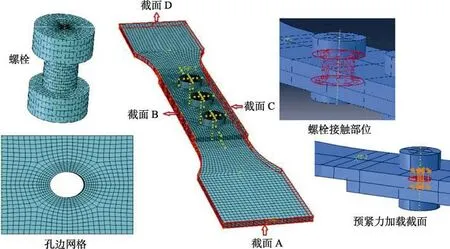
图4 有限元模型Fig.4 The finite element model

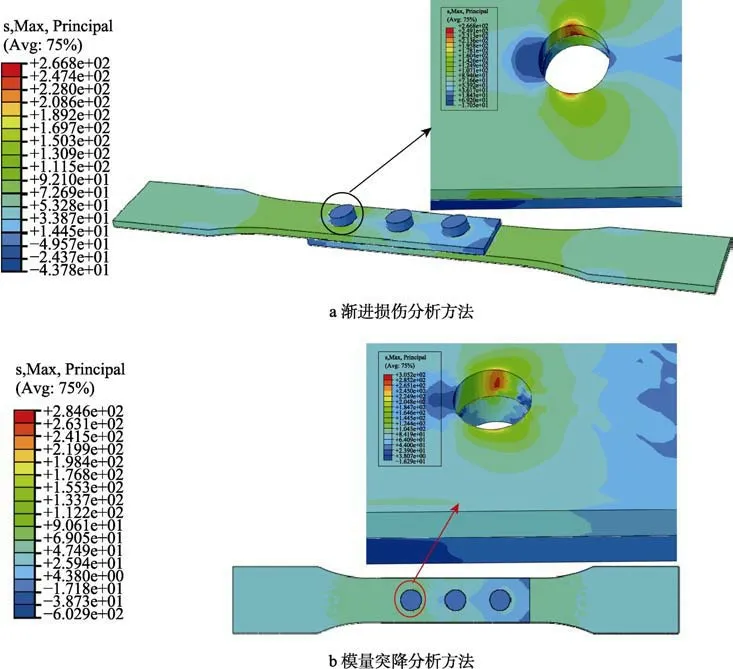
图5 连接结构最大主应力分布Fig.5 Maximum principal stress distribution of connection structure: a) progressive damage analysis method; b) modulus plunged by analysis method

结构局部拉伸损伤失效情况如图6 所示。失效位置相同，均位于连接件第一个孔边的部位，和试验结果一致。渐进损伤分析方法的场分布相对比较均匀，模量突降分析方法依然存在局部突变的情况。

图6 局部拉伸损伤失效情况Fig.6 Local tensile damage failure situation: a) progressive damage analysis method; b) modulus plunged by analysis method; c) test results

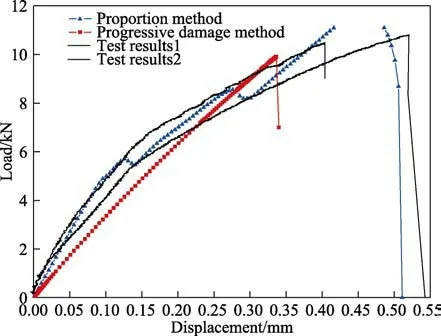
图7 载荷-位移曲线Fig.7 Load-displacement curve

两种方法对于连接结构载荷-位移曲线的计算结果与试验数据的对比如图7 所示。由于模量突降分析方法在数学模型设计过程中根据连接结构试验数据对表1 中基体开裂模量的折减系数进行了调整，因此计算获得的载荷-位移曲线整体趋势上和试验数据取得了较好的一致性，但是存在两个明显的突降和阶 跃。渐进损伤分析方法整体真实模拟了C/SiC 复合材料结构受载过程中的渐进损伤过程，但载荷-位移曲线和试验值误差稍大。试验件1 的破坏载荷为10.5 kN，试验件2 的破坏载荷为10.8 kN，平均为10.65 kN。渐进损伤分析方法计算的破坏载荷为9.9kN，预测误差为 7.0%；模量突降分析方法计算的破坏载荷为11.7 kN，预测误差为9.9%。

通过以上比较分析，模量突降方法通过典型结构的强度试验，调整中间损伤状态模量的折减系数，预测连接结构载荷-位移曲线及最后破坏载荷具有较高的精度。由于采用线性模型过于简化，未考虑C/SiC复合材料受载过程中不同载荷作用下的不同力学行为，针对复杂结构的细节应力-应变分布预测精度相对比较差，且计算获得的载荷-位移曲线存在明显的阶跃现象。这是由于计算过程中，部分单元由于发生基体开裂，引起了刚度退化，使得载荷发生下降。随着加载的继续，相邻的单元继续承载，从而使得载荷继续增大，呈现出阶跃的特征。计算过程中，通过调整基体开裂后刚度退化系数（文中的刚度退化系数取为0.47），使得计算的载荷-位移曲线能够维持在两组试验曲线之间。

渐进损伤分析方法的数学模型来源于C/SiC 材料级力学性能试验数据，能够精确模拟复合材料多种载荷作用下的复杂力学行为，在简单结构的力学行为与失效分析中具有较高的模拟精度。对于复杂连接结构，开孔部位切断了纤维，导致连接板局部开孔周围性能削弱，而螺栓紧固件对结构又存在一定加强作用，采用基于材料级力学性能试验数据建立的本构模型无法真实模拟局部连接区域的受力特征及应力应变状态。因此，虽然渐进损伤分析方法的物理过程模拟比较合理，但是由于局部连接接触部位材料力学性能考虑不充分，导致整体连接结构的载荷-位移关系预测误差略大。

3 结语

围绕C/SiC 陶瓷基复合材料连接结构失效分析问题，对几种不同的复合材料失效准则进行了验证与分析。研究表明，改进三维Hashin 失效准则在预测C/SiC 复合材料结构失效行为时具有较可靠的精度。发展了模量突降和渐进损伤两种分析方法，结合改进三维Hashin 失效准则，基于Abaqus 软件平台编写了有限元分析子程序，针对典型C/SiC 复合材料连接结构进行了失效行为计算分析，获得结构的失效模式与试验结果规律一致，破坏载荷的预测误差在10%以内。通过与试验结果的对比分析，验证了两种方法的有效性，发展的失效分析方法能够为飞行器复合材料热结构的强度分析提供技术支撑。