温度对平流层飞艇囊体材料渗漏性能的影响
2020-02-27袁明清赵海涛陈政李若薇陈吉安
袁明清,赵海涛,陈政,李若薇,陈吉安
(上海交通大学,上海 200240)
浮空气体渗漏率是浮空器蒙皮材料的重要设计参数之一,直接影响浮空器的驻空时间和成本。对于平流层飞艇而言,在其服役过程中,补充浮空气体几乎不可能实现,因此浮空气体的渗漏将直接影响飞艇的飞行与驻空能力。高性能的飞艇囊体材料一般采用阻氦层等阻隔结构来降低浮空气体渗漏,但飞艇的表面积巨大,即使单位表面积的氦气渗漏率较低,长时间的服役仍不可避免地渗漏氦气,导致浮力不足或囊体负压的情况[1]。此外,由于平流层飞艇在服役期间经历昼夜循环,昼夜温度的变化也对飞艇囊体的氦气渗漏以及囊体内外压差造成影响。徐向华等[2]研究了平流层飞艇在高空大气环境中的全天温度变化规律。李小建[3]研究了临近空间浮空器热力学与结构力学的相互作用,并预测了飞艇内部浮空气体的温度变化特性,为飞艇服役过程中昼夜循环温度下的渗漏特性分析提供了理论、数据基础。
复合材料的渗漏行为包括扩散渗透和微裂纹泄露两种方式。微裂纹导致的浮空气体泄露是指在外载荷或环境温度变化的作用下,飞艇囊体材料的涂层内部产生微裂纹,当微裂纹在囊体的厚度方向形成贯穿的渗漏路径时,就发生了气体渗漏。试验研究表明[4],流体分子通过贯穿渗漏路径时的有效渗漏率比仅由扩散渗透引起的有效渗漏率高3 个数量级。在生产制备的过程中,应尽量避免飞艇囊体蒙皮材料微小损伤的产生,但平流层飞艇在昼夜循环温度环境下,囊体内外压差发生变化,微裂纹的产生在所难免,因此研究飞艇在变温环境下的氦气渗漏特性可以从微裂纹分析入手。
国内关于蒙皮材料涂层微裂纹导致的氦气渗漏率研究较少。刘东旭等[5]将氦气的扩散渗漏率转换为当量微孔损伤尺寸,通过当量微孔损伤来反映扩散渗漏和损伤渗漏的共同作用,并对正球形高空浮空器的渗漏特性及驻空时长进行了量化分析。文中采用细观力学有限元方法,通过微裂纹密度以及平均裂纹开口大小求解氦气渗漏路径的横截面积,进而预报飞艇囊体的初始渗漏速率。分析了昼夜循环温度下飞艇囊体的渗漏速率及内外压差的变化情况,对平流层飞艇的设计具有指导意义。
1 飞艇囊体材料初始渗漏速率
1.1 复合材料的刚度退化模型
根据复合材料的特点与试验规律[6],对含有微裂纹的飞艇囊体材料的涂层进行理想化假设:横贯裂纹贯穿厚度方向;整个裂纹代表性体积元为线弹性材料;横贯裂纹严格周期性排列;裂纹断口的上下顶端的裂纹开口大小为0,即裂纹代表性体积元的上下顶端完全连续。这些理想化假设在细观力学的刚度退化模型或宏观力学有限元模型中都适用。
含有一定裂纹密度的裂纹单胞模型如图1 所示,尺寸为2L×2W×2h,且含裂纹的囊体材料可以等效为周期性分布的裂纹代表性体积元。由于裂纹断口的存在,裂纹代表性体积元所代表的蒙皮材料弹性刚度下降(主要是2 方向弹性模量的降低)。定义囊体材料中的裂纹密度为ρ,即每毫米的横贯裂纹数量,裂纹代表性体积元模型2 方向的长度为2L,则:

对不同裂纹密度的蒙皮材料赋予材料参数,并进行基于细观力学有限元的复合材料等效参数计算,可以得到随裂纹密度变化的飞艇囊体材料的等效材料参数,表示为E1(ρ)、E2(ρ)、E3(ρ)、ν23(ρ)、ν13(ρ)、ν12(ρ)、G23(ρ)、G31(ρ)、G12(ρ)。同时得到各裂纹代表性体积元的裂纹开口大小,并计算单位应变下的平均裂纹开口大小,用u(ρ)表示。
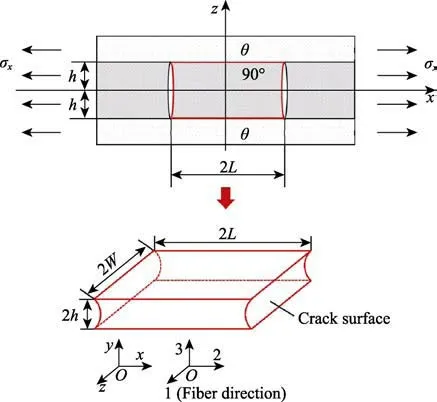
图1 裂纹单胞模型示意图Fig.1 Schematic diagram for unit cell model of crack
1.2 裂纹密度与应变关系推导
考虑尺寸为2h×2W×2L 的代表性体积元,如图2a 所示。分别对裂纹密度为0 和ρ 的两个代表性体积元施加相同的载荷P1,且P1=A×σ2(ρ)=4hW×σ2(ρ)。则在载荷下相应地产生位移v1、v2,如图2b 所示。

图2 代表性体积元示意Fig.2 Representative volume element: a) representative volume element of crack geometry size; b) loading of representative volume element
由于裂纹密度为ρ 的代表性体积元发生了材料刚度退化,在载荷相同的情况下有v1>v2。假设载荷P1均匀作用在代表性体积元2 方向的表面上,且根据正交各向异性材料的平面应力状态,复合材料代表性体积元的本构关系可以表示为:

1.1 节中求解得到的弹性参数与裂纹密度一一对应,是瞬时状态下的材料刚度退化。根据线弹性断裂力学理论中的恒载荷情形,2 方向的应力分量与裂纹密度的关系可以由式(3)计算:

式中:Gmc为囊体材料涂层的临界断裂能量释放率。
式(3)中的裂纹密度ρ、各裂纹密度下2 方向的弹性模量E2(ρ)为已知,涂层临界断裂能量释放率Gmc为材料相关的常数,则可以求出裂纹密度从0~ρ时所需的加载应力大小σ2(ρ),σ2(ρ)也可以看作复合材料囊体微裂纹的萌生应力。由于在宏观的飞艇结构有限元分析中,没有考虑复合材料囊体在产生涂层微裂纹后的刚度退化,按照相同应变情况进行换算,得到的宏观飞艇有限元分析获得的应力场结果σ2(ρ)'与微裂纹密度ρ 之间的关系为:

式中:L0为宏观飞艇有限元分析中2 方向的有限单元尺寸;等式右边第一项表示复合材料囊体宏观结构中初始微裂纹产生时的应力大小。
2 循环温度下的渗漏特性预报
飞艇囊体在制造、充气、上升、驻空过程中都会导致囊体材料涂层微裂纹的产生,微裂纹相互交错并形成气体渗漏路径时,就发生了飞艇气体渗漏。飞艇在到达工作高度后,在高空大气压强、第一次升温的共同作用下,飞艇囊体承受的内外压差是整个服役过程中的最大值,导致飞艇囊体中产生涂层微裂纹,并形成气体渗漏路径。在后续昼夜循环温度的作用下,由于温度、飞艇浮空气体压力的变化,飞艇囊体发生持续但不匀速的气体渗漏。飞艇囊体在循环温度下的渗漏特性预报分为两个步骤进行:囊体初始渗漏率预报;温度循环下持续渗漏模型。
对飞艇囊体建立宏观有限元模型,并在囊体内部加压,压力大小为假设飞艇不发生浮空气体渗漏时,从地面上升到工作高度并伴随温度变化时囊体承受的最大内外压差。一般来说,飞艇的内压比外大气压高一定的百分比[7],可以根据内外压差的控制确定飞艇整个服役过程中的最大压差值ΔPmax。对飞艇囊体的宏观有限元模型加载压力ΔPmax,并求解计算,可以获得飞艇在最大压差条件下的应力场、应变场、位移场结果。
根据囊体各有限单元的应力结果,按照式(4)可以计算该有限单元的裂纹密度ρi。该有限单元的平均裂纹开口大小ui由宏观应变分量εi2及相应裂纹密度代表性体积元在单位应变下裂纹开口大小u(ρi)按照式(5)计算:

式中:下标i 表示宏观有限元的单元编号。
在囊体材料中形成的浮空气体渗漏路径在垂直方向的涂层微裂纹交叉点处产生[8],浮空气体的渗漏路径横截面近似为四边形,则一个有限单元中渗漏路径的横截面积由式(6)计算:
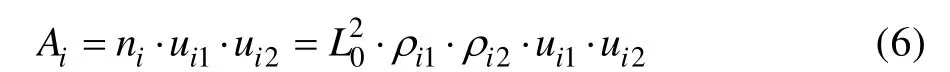
式中:ui1、ui2分别表示宏观有限元坐标系下1、2 方向的平均裂纹开口大小;ni为该有限单元涂层微裂纹的交叉点数量,由各方向裂纹密度计算。
则飞艇囊体的渗漏路径横截总面积为:

式中:n 为飞艇囊体的有限单元数量。
为有效描述飞艇囊体在服役过程中浮空气体渗漏量的变化情况,根据气体渗漏路径横截总面积以及囊体内外压差,可以计算浮空气体的渗透量。由伯努利方程推导出的渗漏流量与渗漏路径横截面积的等式关系为:

式中:dmH为渗漏的浮空气体质量微元;ρH为浮空气体密度。
飞艇囊体材料的渗漏速率Q 表示为:

3 算例与讨论
3.1 飞艇囊体材料的微裂纹密度
文中采用的飞艇囊体材料参数:密度为730.769 kg/m3(面密度为 95 g/m2),弹性模量 E= 6.9 GPa,泊松比ν=0.45,厚度t=0.13 mm[5],涂层临界断裂能量释放率Gmc=156 J/m2[9]。飞艇囊体材料的代表性体积元尺寸为 2h×2W×2L=0.13 mm×1 mm× (1/ρ) mm,ρ 为涂层微裂纹密度。
通过细观力学有限元分析,飞艇囊体材料的弹性模量及泊松比随裂纹密度增加而衰减。定义正则化弹性模量E(0)/E(ρ)以及正则化泊松比ν(0)/ν(ρ),正则化的弹性模量及泊松比随涂层微裂纹密度的变化如图5 和图6 所示。飞艇囊体材料的弹性模量和泊松比随涂层微裂纹密度的变化趋势相似,在涂层微裂纹密度达到0.8 mm-1时,材料参数均下降到原始参数的0.713 倍。

图3 弹性模量随涂层微裂纹密度变化Fig.3 Elastic modulus changing with coating micro crack density

图4 泊松比随涂层微裂纹密度变化Fig.4 Poisson′s ratio changing with coating micro crack density
通过线弹性断裂力学分析,获得飞艇囊体响应应力与微裂纹密度的关系如图7 所示。在飞艇囊体材料应力达到175.484 MPa 时,囊体材料中开始产生涂层微裂纹,并且随着响应应力增加,涂层微裂纹密度也随之增大。
3.2 飞艇囊体宏观有限元模型
平流层飞艇的经典几何外形[10]如图8 所示。采用经典双椭圆形状,其中a=75 m,b=25 m,囊体厚度t=0.13 mm。飞艇总长为181.066 m,最大直径为50 m。在有限元软件中,建立的飞艇几何模型及网格划分如图9 所示。有限单元网格尺寸约3 m,采用四边形膜单元M3D4。

图5 飞艇囊体材料的涂层微裂纹密度随响应应力的变化Fig.5 Airship capsule material coating micro crack density along with the change of stress response
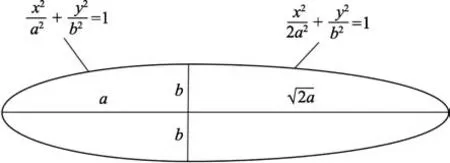
图6 平流层飞艇经典外形Fig.6 Classic shape of stratosphere airship

图7 飞艇囊体的几何模型及网格划分Fig.7 Airship capsule of geometric model (a) and mesh (b)
飞艇囊体材料参数同3.1 节,在飞艇左侧端点施加固定约束,内部施加压力载荷ΔPmax=1076.563 Pa。内部施加的压力载荷根据飞艇处于20 km 高空时,保持内部浮空气体平均压强比外界大气高4%,并在第一次升温温差达到266.78 K 时计算。提交飞艇囊体的有限元计算,获得的飞艇囊体响应应力结果与应变结果如图10 所示。

图8 飞艇囊体应力与应变场结果Fig.8 Stress and the strain field results of airship capsule body: a) Mises stress field; b) axial stress field; c) circumferential stress field; d) shear stress field; e) axial strain field (logarithmic strain); f) circumferential strain field (logarithmic strain)
3.3 飞艇囊体初始渗漏率预报
按图7 中的应力与涂层微裂纹密度关系计算,有限单元的平均涂层微裂纹密度为0.0348 mm-1,即一个尺寸为 3 m 的飞艇囊体有限单元中,将产生10899.36 个微裂纹渗漏点。单位应变下有限单元平均裂纹开口大小为0.354 mm,加载条件下的有限单元平均裂纹开口大小约为0.0113 mm,即一个有限单元中平均涂层微裂纹渗漏路径横截面积为1.328 mm2。
根据飞艇的应力、应变场结果,以及线弹性断裂力学分析,计算得该180 m 长的飞艇总渗漏路径横截面积为1295.297 mm2。将上述参数代入式(9),当浮空气体为氦气时(标准大气压下的氦气密度ρH=0.1786 kg/m3),计算得飞艇囊体的初始渗漏率速率为0.295 kg/s,即氦气渗透率为0.736 L/(m2·d)。

图9 20 km 高度飞艇氦气平均温度昼夜变化曲线Fig.9 Diurnal change of average temperature of helium for 20 km altitude airship

图10 飞艇囊体的氦气渗漏速率随时间的变 化曲线Fig.10 Helium leakage rate curve of airship capsule changing over time
3.4 飞艇囊体昼夜循环温度下的渗漏特性预报
根据式(9)表达的飞艇囊体材料的氦气渗漏速率,以及图11 所示的飞艇工作高度昼夜循环温度曲线,则可以求解飞艇驻空过程中的氦气渗漏速率(如图12 所示),且可以通过氦气渗漏质量求得飞艇在昼夜循环温度下的囊体内外压差变化情况。该飞艇在5 天内的囊体内外压差变化曲线如图1 所示。与当量损伤直径方法进行对比,两种方法吻合良好。在昼夜变化导致的循环温度环境中,飞艇囊体的内外压差由初始值65.12 Pa 上升到1068.45 Pa,且在飞艇飞行过程中,不断发生飞艇囊体的氦气渗漏。随着时间推移,不同天的同时刻飞艇囊体内外压差持续降低。飞艇每飞行一天,囊体内外压差最大值下降约20 Pa。
该飞艇在7 天内的囊体内外压差变化曲线如图14 所示。飞艇飞行时间超过120 h 时,在低温条件下, 飞艇囊体内压力略小于外界大气压,因此飞艇的驻空时间在第5 天已经达到极限。

图11 5 天内飞艇囊体内外压差随时间的变化曲线Fig.11 Differential pressure inside and outside airship capsule varying with time in 5 days

图12 7 天内飞艇囊体内外压差随时间的变化曲线Fig.12 Differential pressure inside and outside airship capsule varying with time
4 结论
文中采用细观力学有限元方法,预报了平流层飞艇的初始浮空气体渗漏速率,并计算了飞艇在昼夜循环温度环境下的氦气渗漏速率以及囊体内外压差变化情况。可以得出以下结论:
1)飞艇囊体材料在承载过程中,由于涂层微裂纹导致的浮空气体渗漏将直接影响飞艇的驻空时长。当浮空气体质量一定时,持续的渗漏将导致飞艇内外压差逐渐降低,甚至出现负压情况。
2)飞艇囊体的内外压差与囊体材料断裂性能、工作高度、昼夜循环温度有关。囊体材料的涂层断裂能量释放率越小,飞艇飞行过程中越容易产生高密度的渗漏路径;昼夜温差越大时,飞艇囊体的内外压差变化越显著。
3)通过优化复合材料的生产工艺、飞艇升空与驻空过程的受载状况等方式,可以降低飞艇囊体材料内涂层微裂纹密度,从而达到提高飞艇抗渗漏设计的目的,提高飞艇的驻空能力。
4)细观力学有限元方法能够有效预报飞艇应力与渗漏特性之间的关系,对飞艇囊体的设计加工过程具有指导意义,为平流层飞艇设计提供技术支持。
