基于GA-BP神经网络模型鉴别2型糖尿病性周围神经病变的分类模型研究

黄仕鑫，浦科学，桑祎莹，罗亚玲

1重庆医科大学医学数据研究院，重庆 400016，2重庆市渝北区人民医院人力资源科，重庆 401120；3重庆医科大学医学信息学院，重庆 400016

目前，2型糖尿病的发病率持续增高，已成为严重危害世界各国人民健康的主要慢性非传染性疾病[1]。糖尿病性周围神经病变(diabetic peripheral neuropathy，DPN)属于糖尿病神经病变范畴，是糖尿病最常见的微血管并发症之一[2]，具有起病缓慢、隐匿性强、症状逐渐严重、不易逆转的特点[3]。

DPN可致残、致死，对家庭及社会的经济负担重，目前尚无特效疗法，主要依靠早期发现、早期治疗[4]。对DPN的鉴别诊断主要依靠生化指标、肌电图检查及物理检查等测定，但其临床表现复杂多样，如何早期、准确地进行诊断是目前的研究热点及难点[5-6]。近年来数据挖掘技术广泛应用于医学领域，在疾病诊断、预后预测、风险评估等方面具有良好的应用价值[7-10]，其中决策树模型、贝叶斯模型、神经网络是常见的数据挖掘模型。与算法低效的决策树和泛化性较差的贝叶斯模型相比，反向传播(BP)神经网络有着自学习、自组织等优势；但易陷入局部最优，得到局部最优解；且因BP神经网络模型开始权值和阈值的设定是随机的，使其模型不够稳定。为改善BP神经网络的缺陷，可采用遗传算法优化神经网络的学习过程来弥补。遗传算法能模拟生物进化规律，具有良好的全局寻优能力。有学者将遗传算法和BP神经网络相结合，应用于工业技术等领域，结果显示其具有较好的准确性及可行性[11-14]。本研究创新性地将数据挖掘中的决策树、贝叶斯模型、神经网络方法应用于DPN的诊断预测中，以期为临床诊断提供准确的辅助模型。

1 资料与方法

1.1 临床资料 选取重庆医科大学附属医院内分泌科2016年1－12月收治的DPN患者2240例作为病例组，同期骨科、中医康复科、心血管内科、呼吸内科、泌尿外科等收治的非DPN患者2632例作为对照组。病例组入选标准：①2型糖尿病患者；②符合DPN诊断标准，即以下5项检查中有2项及以上异常：神经传导速度有2项及以上减慢，振动觉异常，温度觉异常，踝反射消失，足部感觉消退；③病历中主要诊断为DPN。对照组入选标准：①非DPN患者；②无糖尿病史。两组排除标准：①年龄<18岁；②采集的检验指标缺失值>40%。

1.2 方法

1.2.1 数据处理 对原始数据进行分析整理，对个别有缺失值的样本进行抛弃处理，并对样本数据进行归一化处理。预处理后的数据不仅可以保持原始数据的完整性，而且提高了数据挖掘的运算效率。

1.2.2 观察指标 包括与2型糖尿病患病相关的41项检查指标：性别、年龄、纤维蛋白原、凝血酶时间、部分凝血活酶时间、凝血酶原时间、尿pH值、低密度脂蛋白胆固醇(LDL-C)、高密度脂蛋白胆固醇(HDL-C)、三酰甘油(TG)、总胆固醇(TC)、碱性磷酸酶、尿酸、钙、氯、钠、钾、白蛋白、直接胆红素、总胆红素、谷丙转氨酶、肌酐、尿素、葡萄糖、白细胞计数、单核细胞百分比、血细胞比容、红细胞分布宽度分布系数、红细胞分布宽度标准差、红细胞计数、淋巴细胞百分比、淋巴细胞计数、平均红细胞体积、平均红细胞血红蛋白含量、平均红细胞血红蛋白浓度、血红蛋白、血小板压积、血小板分布宽度、血小板计数、中性粒细胞百分比、中性粒细胞计数。

1.2.3 单因素分析 采用SPSS 21.0软件将2240例病例组与2632例对照组患者的41项指标进行χ2检验或t检验。P<0.05为差异有统计学意义。

1.2.4 决策树模型 采用R软件将计量指标转换为分类指标，采用自顶向下的递归方式建立决策树模型，在每个内部节点进行属性值的比较并判断该节点以下的分支，在叶子节点得到分类的结论。

1.2.5 贝叶斯模型 采用R软件利用先验信息和样本数据信息确定事件的后验概率。

1.2.6 BP神经网络模型 为误差反向传播神经网络模型，因采用BP算法而得名，即以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值[15]。采用MATLAB 2014a软件构建BP及遗传算法优化反向传播(GA-BP)神经网络模型，并将样本随机分为训练样本和测试样本[16]。

1.2.7 BP神经网络设计 ①样本归一化处理：将样本值归一到区间[-1,1]内，对输入输出变量进行归一化处理，提高网络的训练速度，采用χbij=[2×(χij－χij,min)/(χij,max－χij,min)]－1；②确定层数及个数：3层BP网络可以实现任意非线性映射，最适合用于模拟输入输出关系[17]，且训练时间相对较短：网络输入为单因素分析有统计学意义的变量指标，并将这些输入提供给输入层的单元，共计37个。

隐单元数的确定比较复杂，目前仍无理想的解决方法，一般根据多次尝试来确定最优个数；通常使用公式为确定隐单元数的范围[16]，最终确定隐单元数范围为[5,19]。GA-BP神经网络模型将病例组和对照组进行分类，因此输出节点数为1，如果输出值≤0.5，为未患DPN，输出值>0.5为DPN。

1.2.8 BP神经网络的参数选择 隐含层及输出层的传递函数采用S型函数及双极性S型函数：，值域在(0,1)；学习率设置为0.01，训练函数选择L evenberg-Marquardt方法，权重更新方法为梯度下降法：。

1.2.9 遗传算法的设计 ①种群和进化代数：种群规模为50，进化代数为10；②编码：将BP网络的输入层与隐含层的连续权值、隐含层的阈值、隐含层与输出层的连接权值、输出层的阈值进行编码，初始值设置为0；③设定适应度函数：通过寻找适应度函数的最小值来找到最优权值和阈值，使分类识别的输出值与期望值间误差最小[公式为：Error=∑(|simoutputn-outputn|)]；④选择、交叉和变异：采用轮盘赌法选择新个体；选择单点交叉，交叉概率为0.3；变异概率为0.1[18]。

2 结 果

2.1 单因素分析结果 将病例组与对照组的41项指标变量进行比较，除年龄、性别、红细胞计数、血小板压积外，其余37项差异均有统计学意义(P<0.05，表1)。

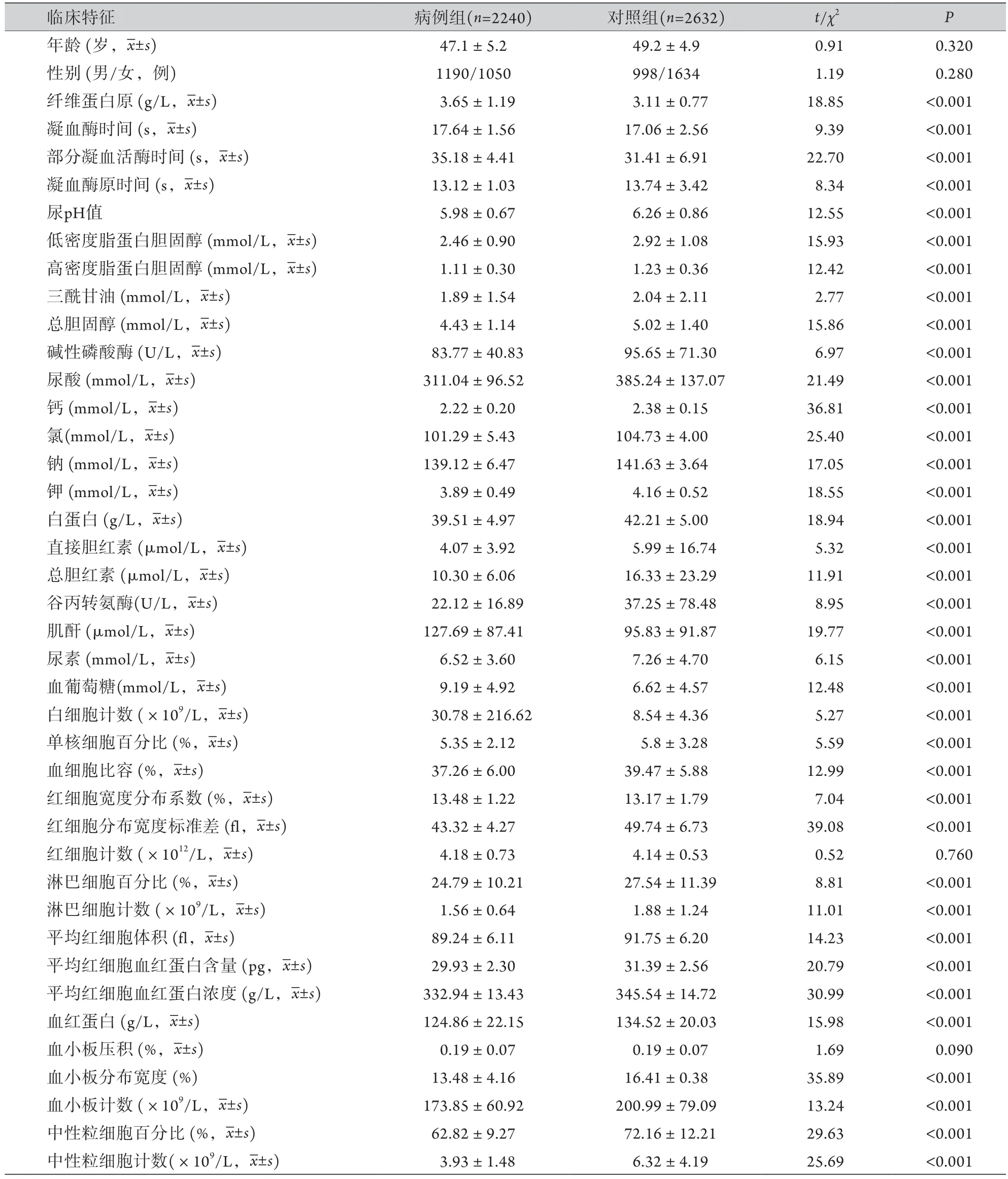
表1 病例组与对照组的41项临床指标比较Tab.1 Comparison of 41 clinical indexes between DPN group and non-DPN group (Univariate analysis of data)

2.2 GA-BP神经网络分类模型 将单因素分析有统计学意义的37项指标纳入GA-BP神经网络模型之中，根据隐单元范围[5,19]分别取其值对训练集进行多次训练；当隐单元数为19时，GA-BP神经网络对数据的拟合效果最好，对训练集和测试集的预测准确率分别达99.51%及99.50%。

2.3 决策树、贝叶斯、BP神经网络及GA-BP神经网络模型比较 GA-BP神经网络模型的准确率最高，贝叶斯模型准确率最低；GA-BP神经网络模型约登指数最高，贝叶斯模型约登指数最低(表2)。

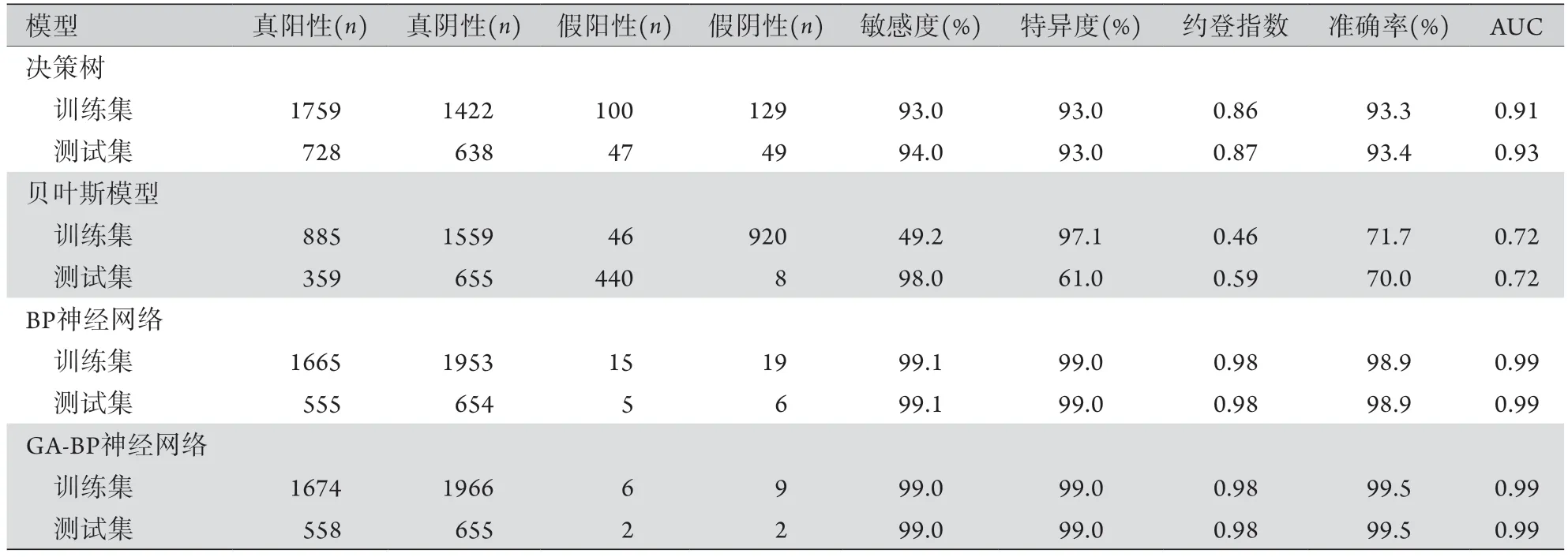
表2 4个模型对DPN的诊断参数比较Tab.2 Comparison of diagnostic parameters of DPN for 4 models

2.4 GA-BP神经网络模型的性能、训练结果及适应度曲线 模型性能用均方误差(MSE)表示，GA-BP神经网络模型的训练集和测试集的性能不断被优化，最终在模型迭代8次处达到最优(图1)；从GA-BP神经网络模型的训练结果可知模型内部的参数和函数选择，且显示了模型结束条件为精度达到预设值0.01(图2)；模型适应度曲线表明模型在不断优化，且最终达到最优(图3)。

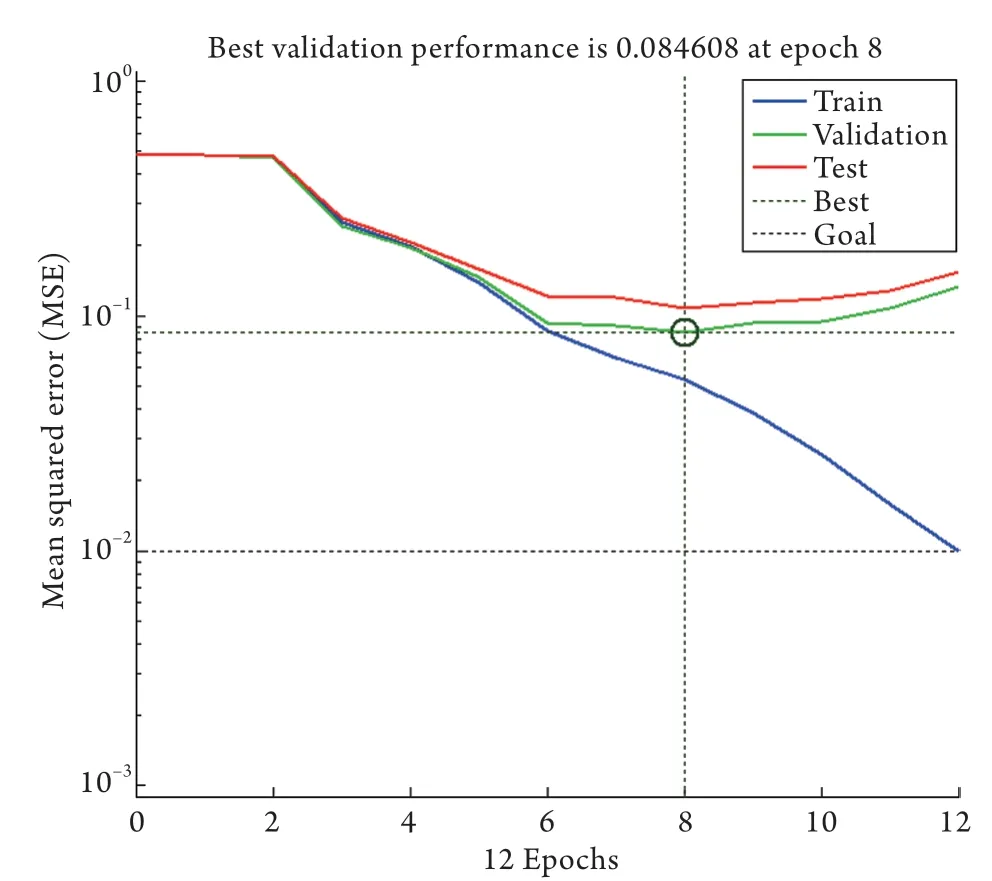
图1 GA-BP神经网络模型的性能Fig.1 Performance of GA-BP neural network model

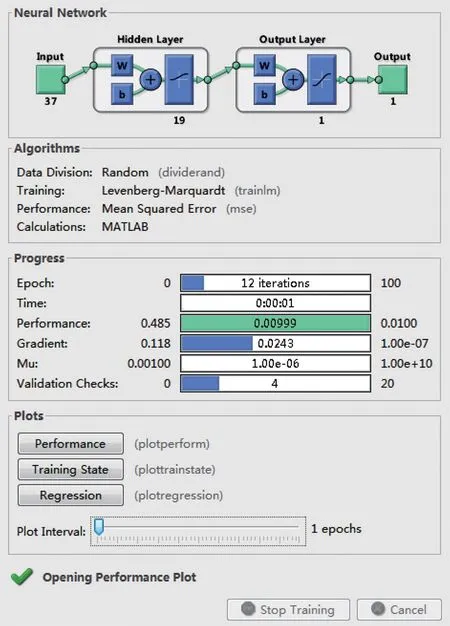
图2 GA-BP神经网络模型训练结果Fig.2 Training results of GA-BP neural network model

3 讨 论

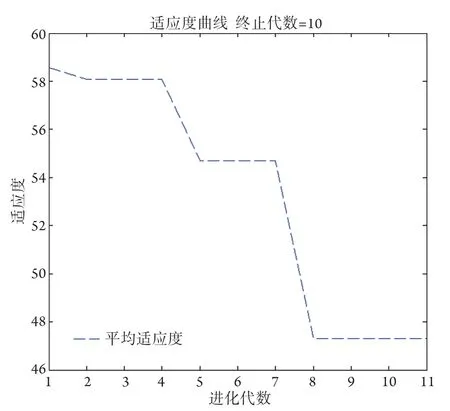
图3 GA-BP神经网络模型的适应度曲线Fig.3 Fitness curve of GA-BP neural network model

DPN是多因素共同作用的结果，其发病机制目前尚不完全清楚。对糖尿病患者和非糖尿病患者发生周围神经病变进行疾病分类预测，不仅可为个人自我保健提供准确的指导，同时还可为医师有效判断DPN提供一定帮助。本研究数据来源于重庆医科大学附属医院2016年1－12月的临床数据，具有良好的同质性；采用决策树、贝叶斯模型、BP神经网络、GA-BP神经网络对DPN进行分类建模，通过比较各项评估参数以衡量各个模型的优劣，为DPN的诊断提供了一种有价值的计算机辅助方法。

经典决策树模型是一种简单但是应用广泛的分类器，通过训练数据构建决策树，可以高效地对未知数据进行分类。其主要优点是具有描述性，有助于人工分析，且分类效率高；缺点是会导致过度拟合。但其在本文中的训练集准确率为93.3%，测试集准确率为93.4%，说明本次建立的决策树模型预测准确率较高。

朴素贝叶斯模型是一种简单有效的常用分类器，指在统计资料的基础上，依据某些特征计算各类别的概率，从而实现分类。其主要优点是有稳定的分类效率，对缺失数据不太敏感，算法也相对简单，缺点是模型假设属性之间是相互独立的，这个假设在实际应用中往往是不成立的，所以会间接影响预测模型的准确率。其在本文中的训练集准确率为71.7%，测试集准确率为70.0%，说明本次建立的贝叶斯模型预测准确率一般。

BP神经网络模型是一种按照误差反向传播算法训练的多层前馈神经网络，以网络误差平方为目标函数，采用梯度下降法来计算目标函数的最小值。其主要优点是具有很强的非线性映射能力和柔性的网络结构，缺点是模型容易陷入局部最小值，网络推广能力有限。其在本文的训练集准确率为98.9%，测试集准确率为98.9%，说明本次建立的BP神经网络模型预测准确率很高。

GA-BP神经网络模型避免了单独观察某一个指标所产生的片面性，解决了DPN各项指标与诊断结果之间的非线性关系，本文中的模型经过12次训练，达到了预期设置的性能指标(MSE=0.01)，其诊断效果得到了很好的验证，且模型的各项评估参数(约登指数、准确率)均高于决策树、贝叶斯模型和BP神经网络模型。

与BP神经网络模型相比，GA-BP神经网络模型虽在各项评估参数上无明显优势，但其具有BP神经网络所不具备的全局寻优和稳定性的特点；BP神经网络存在局部最优的直接原因是自身算法不完善，而遗传算法具有全局寻优的特点；BP神经网络的不稳定性是因为初始权值和阈值是随机产生的，缺乏选择依据，而网络连接权值和阈值的整体分布决定了模型的效果，遗传算法通过编码、选择、交叉、变异得到优化后的权值和阈值，并将其设置为BP神经网络的初始权值和阈值，从而提高模型的稳定性。模型适应度曲线显示，在第4代和第7代突破局部最优解，在第8代达到最优；图1训练集在第8次训练之后MSE呈现下降达到目标精度，反映此模型逼近学习目标的程度优秀(准确性)；模型在训练过程中未出现MSE升高，反映此模型在面对相近规模的不同训练集时，其估计结果较好(稳定性)。GA-BP神经网络模型能应对复杂的大规模数据及无先验知识的资料，有较好的拟合精度。同时神经网络在医学中有着广泛的应用，医学专家可以借助它作出更合理的判断和决策。

本研究的优势：①将所有符合标准的检验项目纳入模型，排除了主观经验选取，避免了选择偏倚；②样本量较大，且患者的检验数据保持了同质性；③GA-BP神经网络模型设置了训练集和测试集以保证结果的真实性和可推广性。但本研究同时具有一定的局限性：①并未得出模型的具体危险因素的权重值；②虽然全面采集了实验室指标，但由于某些指标数据量低于40%，故未纳入分析，其与DPN的关系有待扩大数据量后进一步分析；③GA-BP神经网络模型并不具备专业临床诊断思维，只能对临床医师的诊断决策起辅助作用。