基于变刚度变阻尼的柔性喷管动态模型

胡嘉鑫，薛牧遥，杨敬贤，童 悦，邹 杰，郑 庆，任军学

（1.北京航空航天大学 宇航学院，北京 100191；2.上海航天动力技术研究所，上海 200125）

0 引言

柔性喷管主要由活动体、固定体、柔性接头等部件组成［1］，其与伺服系统共同构成推力矢量控制系统［2］，主要应用于高过载机动飞行的防空导弹及反导导弹中［3-4］。柔性喷管的动态特性主要由柔性接头和伺服系统决定。由于实现摆动的柔性接头中的橡胶材料的黏弹性和摩擦性，柔性喷管在受正弦激励力作用做正弦摆动时，其恢复力矩-摆角曲线会出现迟滞现象，形成迟滞曲线。迟滞曲线受柔性接头工作压强、工作温度、摆动振幅、摆动频率，以及橡胶材料性能等多方面因素的影响［5-6］，使柔性喷管的动态特性变得十分复杂，模型难以将各个因素均考虑在内，影响了控制系统的控制精度［7］。针对柔性接头动态特性问题，通常将柔性接头视作简单的质量-弹簧系统［8］（定刚度定阻尼模型），未考虑摆动振幅、摆动频率对刚度系数和阻尼系数的影响，无法反映迟滞曲线的变化趋势。Naupapac等［9］使用查表法作为柔性接头的运动模型，但只适用于某一振幅下某一频率的迟滞曲线；郑开发等［10］提出了刚度系数可变、阻尼系数可变的柔性接头运动模型，可以预测某一振幅下不同频率的恢复力矩。此外可借鉴橡胶隔振器的研究方法，Markou等［11］将隔振器视为非线性弹簧、弹塑性模块、迟滞阻尼器的组合，可以预测隔振器在同一频率下不同振幅的迟滞曲线，但不能预测同一振幅下不同频率的迟滞曲线。龚宪生等［12］考虑到了隔振器存在的黏性阻尼、干阻尼以及高阶阻尼，构建了新的阻尼模型，该模型能够清晰地反映隔振器中阻尼的组成成分及其大小，但对信噪比要求高，参数识别困难。上述研究对柔性接头的动态模型很有借鉴意义，但除了文献［8］中的定刚度-定阻尼模型和文献［9］中的查表法模型之外，其余研究均未结合伺服机构模型进行研究。

为了更准确模拟柔性接头的迟滞特性，并明确电液伺服机构和柔性接头在系统中的作用，本文将基于柔性接头变刚度-变阻尼模型构造电液伺服机构-变刚度变阻尼模型，与电液伺服机构-定刚度定阻尼模型进行了对比，并研究电液伺服机构不同参数和柔性接头工作参数对模型的影响。

1 柔性接头动态实验

柔性接头的实验装置如图1 所示。该装置由高压气瓶向压力容器填充高压N2模拟柔性接头的工作压力，并通过电液伺服机构驱动作动器产生设定振幅，设定频率的正弦激励力，用于产生柔性接头摆动所需要的摆动力矩。2 个水平安装的位移传感器用来测试柔性接头的摆角，结合铅垂的位移传感器可测量柔性接头的摆心［13］，拉压力传感器用于测试作动器所施加的作用力，在得出摆心和作动力后，按照文献［1］所提到的方式即可计算出作动力矩。

图1 柔性接头实验系统Fig.1 Experimental system for flexible joints

当工作压力为9、6、3 MPa，柔性接头摆动振幅为6°、5°、4°，频率为0.1～1.0 Hz（间隔为0.1 Hz）时，分别测量了摆动力矩随摆动角度的变化关系，即迟滞曲线，相关实验结果如图3（a）、图4（a）、图5（a）所示。柔性接头变刚度变阻尼模型是在实验结果的基础上建立的，并进一步结合电液伺服机构模型构建了电液伺服机构-变刚度变阻尼模型。

2 电液伺服机构-变刚度变阻尼模型

2.1 变刚度变阻尼模型

将柔性接头的摆动力矩分解为惯性力矩MI=其中，I为转动惯量，δ为摆角），阻尼力矩Mc=Kr·，以及弹性力矩Mk=Kδ，其角运动符合二阶非线性齐次微分方程，即

在之前的研究中，一般将柔性接头简化为刚度系数K和阻尼系数Kr不变的质量-弹簧系统（定刚度定阻尼模型），忽略了摆动振幅、摆动频率、工作压强、橡胶材料特性等对K、Kr的影响［8］。柔性接头的定刚度定阻尼模型与迟滞曲线实验结果吻合较差，且不能反映迟滞曲线随频率的变化趋势（参见2.3 节）。本文采用了刚度系数与阻尼系数均可变化的模型（变刚度变阻尼模型）［10］，预测某一摆动振幅下不同摆动频率的恢复力矩与摆角之间的关系。

在变刚度-变阻尼模型中，仍将恢复力矩M分解为弹性力矩Mk、阻尼力矩Mc、惯性力矩MI3 部分，所不同的是刚度系数可随频率f变化，弹性力矩为Mk=K0+K1·δ+K2·δ2+K3·δ3，阻尼系数也可随频率f变化，阻尼力矩为Mc=c·，

根据第1 节的试验方法得到摆动力矩-摆角试验数据后，在某一振幅下4 组不同频率迟滞曲线实验结果（频率分别为0.1、0.4、0.7、1.0 Hz）的基础上，运用最小二乘法对刚度系数和阻尼系数进行识别，可得到该振幅下刚度系数和阻尼系数关于频率的函数关系，函数形式为

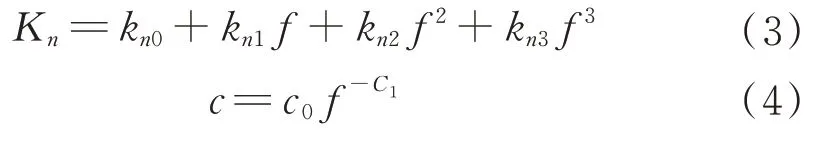
2.2 电液伺服机构

柔性喷管的动态特性不仅取决于柔性喷管本身，也取决于与之匹配的伺服系统［8，14］。本模型采用电液伺服系统作为柔性喷管的伺服系统。为方便分析，忽略电液伺服机构的非线性因素、结构变形、油泵动态、蓄能器影响等因素，所构建的信号综合方程为

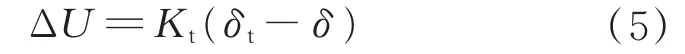
式中：δt为指令摆角；Kt为反馈系数；ΔU为误差信号。

伺服器放大变换方程为

式中：Kui为放大器静态放大系数；IV为放大器的输出电流。

电液伺服机构一阶传递函数为

式中：YV为阀芯的真实位移；Ks为电液伺服机构增益；ωs为电液伺服阀一阶表现频率。

流量分配方程［8］为

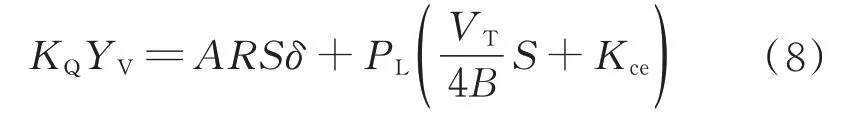
式中：δ为实际摆角；KQ为滑阀流量增益；A为作动器的活塞面积；R为力臂长度；PL为滑阀负载压差；B为油液容积弹性模数；VT为受压容积；Kce为总压力流量系数。

结合柔性接头变刚度变阻尼模型，由于电液伺服机构作动器所提供的力矩M=ARPL和柔性接头变刚度-变阻尼模型的摆动力矩M=Mk+Mc+相等，则可得方程

结合式（5）～式（9）构建电液伺服机构-变刚度变阻尼模型，如图2 所示。

图2 电液伺服机构-变刚度变阻尼模型示意图Fig.2 Schematic diagram of the electro-hydraulic servo mechanism-variable stiffness and variable damping model

2.3 电液伺服机构-变刚度变阻尼模型与电液伺服机构-定刚度定阻尼模型的对比

摆动频率对迟滞曲线影响如图3 所示。图3（a）为柔性接头在不同摆动频率作用下的迟滞曲线实验结果。由图3（a）可以看出：随着频率的增加，迟滞曲线所围成的面积稍有增大，在0°摆角位置的力矩稍有增大，迟滞曲线沿顺时针方向发生了转动。图3（b）为不同摆动频率作用下的电液伺服机构-定刚度定阻尼模型迟滞曲线。由图3（b）可以看出：随着频率的增加，迟滞曲线所围成的面积大幅增加，在0°摆角位置的力矩也大幅增大，迟滞曲线不发生转动，与图3（a）实验结果相差较大。图3（c）为不同摆动频率下的电液伺服机构-变刚度变阻尼模型迟滞曲线。由图3（c）可以看出：与电液伺服机构-定刚度定阻尼模型相比，电液伺服机构-变刚度变阻尼模型所构造的迟滞曲线可以更加准确地与实验结果相吻合，并符合实验结果随频率变化的规律。

3 柔性接头工作参数对电液伺服机构⁃变刚度变阻尼模型的影响

为了明确柔性接头工作参数对电液伺服机构-变刚度变阻尼模型的作用，需研究柔性接头工作压强、摆动振幅等参数对电液伺服机构-变刚度变阻尼模型迟滞曲线和动态响应的影响。

柔性接头工作压强对系统迟滞曲线影响如图4所示。图4（a）为柔性接头在不同工作压强下的迟滞曲线实验结果。由图4（a）可以看出：随着柔性接头工作压强的增大，迟滞曲线所围成的面积增大，在0°摆角位置的力矩增大，迟滞曲线沿顺时针发生了转动。图4（b）为柔性接头不同工作压强作用下的电液伺服机构-变刚度变阻尼模型迟滞曲线。由图4（b）可以看出：电液伺服机构-变刚度变阻尼模型所构造的迟滞曲线可以准确地与实验结果相吻合，并符合实验结果随压强变化的规律。

摆动振幅对系统迟滞曲线影响如图5 所示。图5（a）为柔性接头在不同摆动振幅作用下的迟滞曲线实验结果。由图5（a）可以看出：随着摆动振幅的增大，迟滞曲线所围成的面积增加，在0°摆角位置的力矩增大，并沿逆时针旋转。图5（b）为不同摆动振幅作用下的电液伺服机构-变刚度变阻尼模型迟滞曲线。由图5（b）可以看出：电液伺服机构-变刚度变阻尼模型所构造的迟滞曲线可以准确地与实验结果相吻合，并符合实验结果随振幅变化的规律。

此外由图4 还可以看出：电液伺服机构-变刚度变阻尼模型迟滞曲线的最大振幅及其对应的力矩相对迟滞曲线实验结果较小一些。这是由于当有指令δc输入，系统会产生与之相对应的跟随输出δ，跟随输出δ将产生惯性力矩MI、阻尼力矩Mc、弹性力矩MK，系统需要建立压差力矩M=ARPL以平衡MI、Mc、MK之和，从而产生压差PL，在流量压力系数有限的情况下（Kce≠0），系统需产生一定的偏差Δδ=δ−δc用来弥补压差PL所引起的流量变化，使得跟随输出δ相对指令输入δc较小，电液伺服机构-变刚度变阻尼模型迟滞曲线最大振幅及其所对应的力矩相对实验结果较小。图5中摆动振幅对系统迟滞曲线影响的原因同理。

图3 摆动频率对迟滞曲线影响Fig.3 Effects of the oscillating frequency on the hysteresis curves

图4 柔性接头工作压强对系统迟滞曲线影响Fig.4 Effects of the flexible joint working pressure on the hysteresis curves

4 伺服机构参数对电液伺服机构⁃变刚度变阻尼模型的影响

为了明确电液伺服机构对电液伺服机构-变刚度变阻尼系统的作用，需研究电液伺服机构反馈系数Kt、放大器静态放大系数Kui、电液伺服机构一阶表现系数Ks、电液伺服机构一阶表现频率ωs、滑阀流量增益KQ、作动器活塞面积A、力臂长度R等伺服机构主要参数对电液伺服机构-变刚度变阻尼模型迟滞曲线和动态响应的影响。由于电液伺服机构-变刚度变阻尼模型可简化为图2中的形式，则可将Kt、Kui、Ks、KQ视作KtKuiKsKQ，将A、R视作AR。

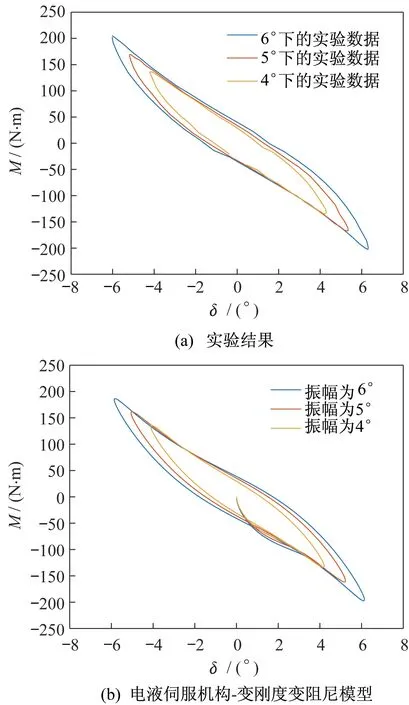
图5 摆动振幅对系统迟滞曲线影响Fig.5 Effects of the oscillating amplitude on the hysteresis curves

图6为KtKuiKsKQ增大为设定值的2 倍、保持不变以及缩小为设定值的1/2 后对系统动态特性的影响。图6（a）为不同KtKuiKsKQ作用下的系统闭环幅频特性曲线。由图6（a）可以看出：随着反馈系数Kt、放大器静态放大系数Kui、电液伺服机构增益Ks、滑阀流量增益KQ的增加，带宽变大，响应也随之变快。图6（b）为不同KtKuiKsKQ作用下的电液伺服机构-变刚度变阻尼模型迟滞曲线。由图6（b）可以看出：电液伺服机构-变刚度变阻尼模型迟滞曲线的最大振幅及其对应的力矩相对迟滞曲线实验结果较小，且变小程度随着Kt、Kui、Ks、KQ的增大而变小。图6（c）为不同KtKuiKsKQ作用下的电液伺服机构-变刚度变阻尼模型动态响应曲线。由图6（c）可以看出：随着Kt、Kui、Ks、KQ的增大，响应速度变快，振荡变剧烈，超调量增加，稳态误差减小。由此可见，Kt、Kui、Ks、KQ对系统动态影响很大。

图7为作动器活塞面积A与力臂长度R的乘积AR增大为设定值的2 倍、保持不变以及缩小为设定值的1/2 后对系统动态特性的影响。图7（a）为不同AR作用下的系统闭环幅频特性曲线。由图7（a）可以看出：随着作动器活塞面积A、力臂长度R的增加，带宽变大，响应也随之变快。图7（b）为不同的AR作用下的电液伺服机构-变刚度变阻尼模型迟滞曲线。由图7（b）可以看出：随着作动器活塞面积A、力臂长度R的增大，电液伺服机构-变刚度变阻尼模型迟滞曲线在振幅最大处的相对迟滞曲线实验结果变宽。图7（c）为不同作动器活塞面积A、力臂长度R作用下的电液伺服机构-变刚度变阻尼模型动态响应曲线。由图7（c）可以看出：随着作动器活塞面积A、力臂长度R的增大，响应速度变快，超调量、振荡次数、调节时间、稳态误差均减小。

图6 Kt、Kui、Ks、KQ对系统动态特性影响Fig.6 Effects of Kt，Kui，Ks，KQon the dynamic characteristics of the system

图7 由作动器活塞面积A 与力臂长度R 的乘积AR 对系统动态特性影响Fig.7 Effects of the product（AR）of the piston area of the actuator（A）and the length of the moment arm（R）on the dynamic characteristics of the system

图6中Kt、Kui、Ks、KQ对系统动态特性影响的原因是：当有指令δc输入，系统会产生压差PL以及用来弥补压差PL所引起的流量变化的偏差Δδ=δ−δc，而当Kt、Kui、Ks、KQ增大时，单位偏差可以产生更大的流量变化，则可以用更小的偏差Δδ来弥补压差PL所造成的流量变化。因此Kt、Kui、Ks、KQ增加，系统所产生的偏差Δδ减小（见图6（b））；稳态误差减小（见图6（c））；相同频率下，闭环幅频特性曲线所对应的对数幅频值增大，闭环幅频特性曲线衰减减慢，带宽随之增加（见图6（a））。此外，当摆角到达最大值附近时，速度很小，接近于0，目标角与输出角之差约等于稳态误差，而随着Kt、Kui、Ks、KQ的增加，稳态误差减小，电液伺服机构-变刚度变阻尼模型迟滞曲线最大振幅及其力矩也随之增加。图7中AR对系统动态特性影响的原因同理。

由图6 和图7 还可以看出：作动器活塞面积A、力臂长度R对系统动态特性影响次于电液伺服机构反馈系数Kt、放大器静态放大系数Kui、电液伺服机构一阶表现系数Ks、滑阀流量增益KQ。

图8为电液伺服阀频率ωs对系统动态特性的影响。图8（a）为不同ωs作用下的系统闭环幅频特性曲线。由图8（a）可以看出：随着ωs的增加，带宽基本不变。图8（b）为不同ωs作用下的电液伺服机构-变刚度变阻尼模型迟滞曲线。由图8（b）可以看出：ωs对迟滞曲线影响不大。图8（c）为不同ωs作用下的电液伺服机构-变刚度变阻尼模型动态响应曲线。由图8（c）可以看出：随着ωs的增大，动态响应曲线的超调量略增加，响应速度、调节时间、稳态误差的变化均不大。综上所述，电液伺服阀频率ωs远大于系统带宽频率，对系统的动态特性基本无影响。

图8 ωs对系统动态特性影响Fig.8 Effects of ωson the dynamic characteristics of the system

5 结束语

本文结合电液伺服机构和柔性接头变刚度-变阻尼模型，构造了柔性喷管的电液伺服机构-变刚度变阻尼模型，分析了不同参数对电液伺服机构-变刚度变阻尼模型动态特性的影响，并和柔性喷管的电液伺服机构-定刚度定阻尼模型相比较。分析结果表明：与电液伺服机构-定刚度定阻尼模型相比，电液伺服机构-变刚度变阻尼模型所构造的迟滞曲线可以更准确地与迟滞实验结果相吻合，预测实验结果随频率变化的规律，并可以准确地模拟不同工作压强、振幅条件下的柔性接头迟滞曲线实验结果；电液伺服机构反馈系数、放大器静态放大系数、电液伺服机构增益、滑阀流量增益对系统动态特性的影响最为显著，作动器活塞面积、力臂长度对系统动态特性影响次之，电液伺服阀一阶表现频率对系统动态特性影响最小。此外，值得注意的是，本文所构造的模型只能预测迟滞曲线实验结果随频率的变化规律，无法对实验结果随振幅、压强的变化规律进行预测，在之后的工作中将针对这一问题进行改进。