空间伸展臂热应变与热变形光纤监测技术
2020-02-26黄居坤于惠勇李翔宇张旭苹
黄居坤,王 勇,曾 捷,,于惠勇,吴 肖,卢 李,李翔宇,张旭苹
(1.南京航空航天大学机械结构力学及控制国家重点实验室,江苏南京 210016;2.上海宇航系统工程研究所结构系统研究室,上海 201109;3.南京大学智能光传感与调控技术教育部重点实验室,江苏南京 210093)
0 引言
空间伸展臂作为一种基本的可伸展结构,不仅是卫星天线系统的重要组成部分,还可以用于太阳帆板和望远镜支架、太空机械手以及空间平台等[1-2]。以方形管为单元的空间伸展臂结构,具有收展原理简单、易调节、调节精度高等特点。
卫星天线在轨运行时长期处于高低温循环热载荷作用下,其本体结构在不均匀热载荷作用下存在热胀和冷缩效应,不可避免地产生热应变,导致结构热变形以及疲劳损伤,降低了卫星天线指向精度,进而影响卫星天线在轨运行的可靠性[3-5]。
空间伸展臂在轨服役过程中热属性监测参量主要包括:温度、热应变以及热变形等。如何准确快速测量这些参量,对于未来实现航天器结构形态感知和在轨健康状态辨识具有重要意义。黄桂平等[6]针对真空环境高低温载荷下航天器变形监测难点,提出采用数字近景摄影技术,获取卫星天线面板高低温变形。贾卫芳等[7]提出了一种基于温度补偿法的光纤光栅热应变监测方法,用于获取单向板和平纹机织层压复合材料内部应变信息。Sun等[8]提出了一种基于双光纤Bragg 光栅的测量系统,用于测量材料的热膨胀系数与热变形。Kim等[9]利用光纤布拉格光栅(Fiber Bragg Grating,FBG)传感器测量结构热膨胀系数,进而实现对均匀温度载荷下钢结构试件热变形状态监测。但考虑到航天器在轨监测实时性与温度载荷分布的非均匀性特征,如何实现针对非均匀温度载荷作用下空间伸展臂温度、热应变与热变形分布及变化信息的多参量集成在线监测显得至关重要。
FBG 具有监测参量众多、质量小、柔韧性好、耐腐蚀、抗电磁干扰以及易于分布式组网等优点,能够满足航空航天器在轨监测的诸多特殊要求[10-11]。因此,本文选择以铝合金空间伸展臂方形管单元模型为研究对象,提出采用FBG,结合热传导理论,分别实现针对伸展臂温度、热应变以及热变形的在线实时监测。
1 FBG 热应变监测原理
FBG 传感器为一种反射型传感器件,当一束宽带光传输到传感器栅区时,在栅区折射率周期性作用下使得只有特定波长附近的光信号反射,而其他光则没有影响。该特定波长称之为FBG 传感器中心波长λB,中心波长取决于光栅周期Λ与有效折射率neff。根据模式耦合理论,FBG 传感器反射光谱中心波长表达式为[12-13]

由式(1)可以看出,任何引起光栅周期、有效折射率变化的因素都能够使得传感器中心波长发生偏移,基于这一原理,FBG 传感器具有传感能力,如图1 所示。

图1 FBG 传感原理Fig.1 Sensing principle of the FBG sensor
空间服役环境下伸展臂主要受到高、低温热循环载荷作用,FBG 在监测伸展臂由于热胀冷缩产生的热应变时,需要对环境温度、应变两个参量进行解析,分别解耦出两个参量对FBG中心波长偏移量的影响,从而得到伸展臂温度与热应变变化信息。
目前FBG 温度、应变交叉敏感解耦方法大致可以分为4 类:双波长矩阵运算法、双参量矩阵运算法、温度参考光栅法[14]以及温度补偿封装法[15]。本文选择规格相同的FBG1、FBG2 布置于同一待测点,其中,将FBG1 与待测点胶接固连,使得其同时受到温度与热应变的信息,FBG1中心波长偏移量为

式中:α为FBG 线性热膨胀系数;ξ为FBG 热光 系数;Peff为纤芯有效弹光系数;ΔλB为热应变FBG中心波长偏移量。
FBG2 布置于FBG1 所在位置附近,处于仅感温不受力状态,其中心波长偏移量[16]为

式中:ΔλT为温度变化FBG中心波长偏移量。
将式(2)减去式(3),可以得到伸展臂热应变εT为

2 数值仿真
数值仿真采用铝合金材料构成的伸展臂方形管单元模型,见表1。

表1 伸展臂材料参数与尺寸Tab.1 Material parameters and dimensions of the deployable mast
利用ANSYS Workbench 仿真软件,对伸展臂一端保持恒温加载,其他部位与空气接触形成热对流交换。环境温度设置为24℃,热对流交换系数为8 W·m−2·℃,考虑到伸展臂端面截面积较小,故只考虑伸展臂内壁以及外壁与空气之间热对流交换,数值仿真中分别对伸展臂单端施加80℃、120℃、160℃以及200℃4 种温度载荷。
当伸展臂一端受到200℃恒温载荷作用时,结构轴向温度分布、热应变分布以及热变形分布,如图2 所示。
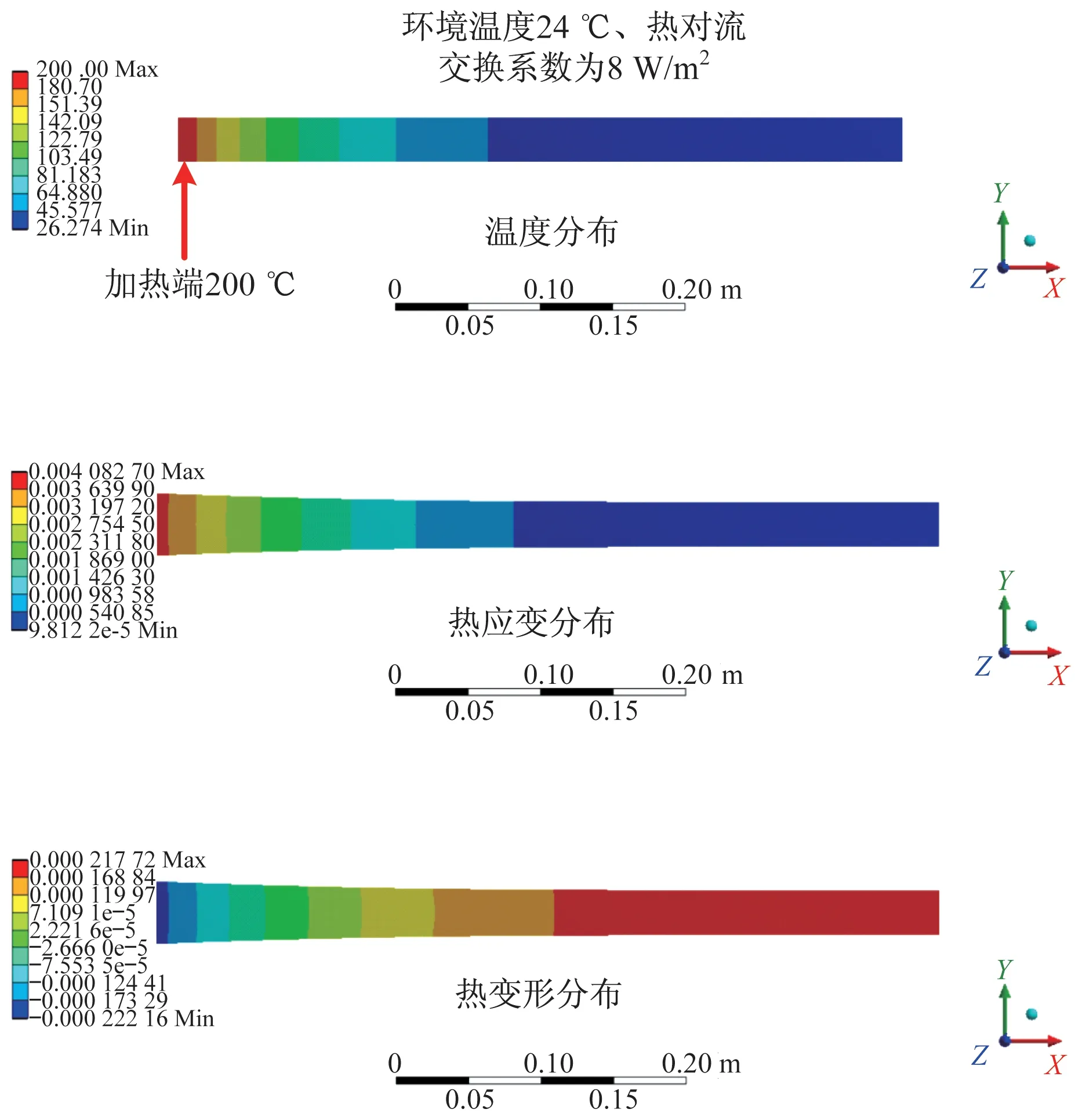
图2 200℃轴向温度、热应变与热变形分布Fig.2 Distributions of the axial temperature,thermal strain,and thermal deformation at 200℃
由图2 可以看出:伸展臂处于单端恒温加载时,热量逐渐由加载端向另一端传递,故温度分布沿着伸展臂轴向呈现递减趋势,在末端趋于稳定。铝合金伸展臂热应变与热变形也呈现类似趋势。在热源附近较大,沿着轴向位置逐渐减小。不同热载荷下伸展臂轴向温度、热应变以及热变形仿真结果如图3 所示。

图3 伸展臂轴向温度、热应变、热变形变化曲线Fig.3 Variation curves of the axial temperature,thermal strain,and thermal deformation of the deployable mast
3 热变形反演计算方法
3.1 基于有限元仿真数据拟合的伸展臂轴向热应变与热变形计算方法
根据图3 可以看出:数值仿真所得温度、热应变以及热变形沿着轴向方向变化曲线类似于指数分布曲线,由此可推导出一种基于有限元拟合法的结构热应变与热变形计算方法。建立伸展臂结构轴向位置坐标系,如图4 所示。图4中,A、C点分别为结构两个端面处,B点位于结构的中点。取xA=0,xB=L/2,xC=L,且A、B、C点应变值ε1、ε2、ε3。

图4 基于3 点应变感知的伸展臂示意图Fig.4 Deployable mast diagram based on three-point strain sensing
根据有限元仿真得到热应变曲线规律呈现指数函数分布,假设伸展臂结构轴向各点热应变变化规律表达式为

式中:a、b、c为关系式系数。根据A、B、C3 点的热应变信息,利用待定系数法,便可得出3 个系数关于热应变值的表达式为

将系数带入式(5),得出伸展臂轴向热应变场函数为

最后计算由于温度变化产生的热变形为

3.2 基于热传导理论的伸展臂轴向温度与热变形计算方法
针对于伸展臂典型方形管结构,不考虑空气与杆件之间的热传导,可将热量等效为一维传播模式。根据热传导理论与能量守恒定律[17-18],在结构达到热稳定状态时,热量的传入与传出相等,即

式中:Qx为微单元在x处导入热量;Qdx+x为微元体在dx+x处导出的热量;Qc为伸展臂热扩散到空气中的热量。

式中:α为热膨胀系数;p为管状结构的长度;λ为导热系数;S为结构的截面积。
整理上述各式可得
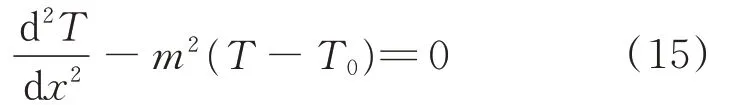
根据式(15),得到其通解为

式中:a和b为通解常数,可由方程边界条件计算得到。
采用单端加热模式,当伸展臂到达热稳定状态时,则其温度边界条件为:x=0 时,T=T(0);x=L时,T=T(L)。
一是全面实施绩效管理。财政部门制定全面实施绩效管理意见,在预算编制、执行和监督环节全面引入绩效管理理念及要求。扩大绩效评价范围,健全绩效评价指标库,完善财政预算管理工作绩效评价机制,将部门预算管理评价结果纳入省级机关绩效考核范围,实现财政管理评价结果与相关支持政策挂钩。
具体情况如图5 所示。

图5 基于两点温度感知的伸展臂示意图Fig.5 Deployable mast diagram based on two-point temperature sensing
将边界条件带入式(16),得出通解常数a和b:

将上述a和b代入式(16),得到方形管伸展臂轴向温度随几何位置分布方程:

由于温度变化产生的热变形计算公式为
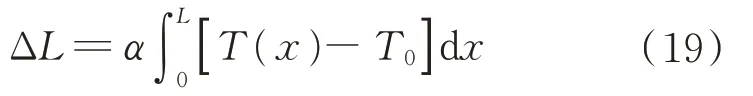
将式(8)带入热变形式(9),通过积分求得伸展臂热变形为

在试验过程中,垂直放置的铝合金方形管伸展臂模型轴向变形包括重力对其的影响,但是重力引起的变形量微小,远小于温度变化引起的热变形,故本文介绍的两种算法均忽略重力引起的微小变形影响,直接监测反演热胀冷缩引起的结构热变形。
4 试验系统
试验对象为铝合金方形管伸展臂缩比模型,结构材料尺寸与仿真模型一致,轴向长500 mm,横截面为边长30 mm 正方形,臂厚为1 mm。试验系统主要由ET-100 加热试验台(加热范围20~350℃,控温精度在±1℃)、用于记录FBG中心波长偏移量的MOI光纤光栅解调仪、用于温度的标定和补偿的Pt100 铂电阻(测温范围为−200~300℃)等设备共同组成。基于分布式光纤传感器的单端热载荷作用下伸展臂温度、热应变与热变形监测试验系统,如图6 所示。

图6 伸展臂温度、热应变与热变形监测试验系统Fig.6 Test system for monitoring the temperature,thermal strain,and thermal deformation of the deployable mast

图7 伸展臂结构表面分布式光纤传感器布局Fig.7 Distributed fiber optic sensor layout on the surface of the deployable mast
5 试验结果与讨论
5.1 伸展臂温度测量与分布反演
通过调节加热台温度,使得伸展臂加热端分别保持80℃、120℃、160℃、200℃恒定温度。依次保持预设温度一段时间,待热电偶显示温度稳定后,记录位于伸展臂轴向不同位置的光纤光栅温度传感器中心波长,如图8 所示。
由图8 可以看出:随着温度升高,各FBG 传感器中心波长向长波方向偏移,且呈现较好线性关系,但由于FBG5 黏贴于伸展臂未加热段,温度变化较小,易受到环境温度影响,导致线性度较差。根据FBG 温度传感原理,将FBG中心波长偏移量转化为伸展臂表面温度值,并与有限元仿真结构进行对比,见表2。
由表2 可以看出:当加热端温度恒定时,伸展臂表面实测温度与有限元仿真所得温度存在一定误差,这是由于仿真条件下轴向热传导及其与空气热扩散效应均匀。而在真实试验中材料属性呈现一定非均匀性,环境温度存在微小变化以及热对流不稳定等因素,会导致实测温度与有限元仿真所得伸展臂轴向温度分布存在稍许偏差。
根据FBG 传感器实测所得各点离散化的温度信息,基于热传导理论,可以反演得到伸展臂轴向温度场分布,并与有限元仿真轴线温度场曲线对比,如图9 所示。

表2 不同温度载荷下伸展臂温度仿真值与光纤传感器实测值对比Tab.2 Comparisons of the temperature simulation values of the deployable mast and the measured values of the fiber optic sensor under different temperature loads
基于热传导理论推导的结构轴向温度场计算方法,构建基于LabVIEW 实时监测系统,导入不同热载荷下FBG 传感器测量所得温度值,反演得到伸展臂结构轴向温度曲线以及温度场云图,如图10所示。
5.2 伸展臂结构热应变测量与分布反演
以80℃作为应变测量基准,将得到温度补偿后的FBG 应变传感器中心波长变化量转化为应变值,并与电阻应变片所测应变值进行对比,得到的结构热应变与温度之间关系曲线,如图11 所示。由图11可以看出:伸展臂温度从80℃变化为200℃时,伸展臂从加热端开始布置的FBG 应变传感器FBG4、FBG3、FBG2、FBG1 测量的最大热应变值分别为776.4、445.3、163.8、109.4 με,呈现递减态势。这是因为热量从加热端向另一端传输,距离越远,热传导的热量越少,伸展臂温度越低,故导致产生的热应变值越小。
根据有限元分析拟合所得伸展臂轴向热应变函数,结合FBG 实测热应变数据,反演得到伸展臂轴向其他位置应变信息,进而重构出整体热应变场。同样以80℃作为基准,将120℃、160℃以及200℃温度下轴向4 个不同位置热应变导入Lab⁃VIEW 可视化实时显示系统,得到伸展臂轴向热应变曲线与应变场云图,如图12 所示。
5.3 伸展臂热变形计算结果与分析
将分布式光纤传感器实测温度信息代入热传导解析法,同时将热应变FBG 实测值代入有限元拟合法,可以计算得到不同温度载荷作用下伸展臂轴向热变形状态。最后将上述两种由FBG 传感器实测数据反演计算所得结果与有限元仿真所得热变形量进行对比,见表3。

图9 伸展臂轴向温度反演曲线与有限元曲线对比图Fig.9 Comparisons of the inversion curve of the axial temperature and the finite element curve of the deployable mast
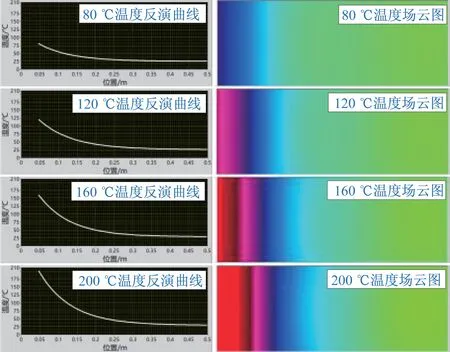
图10 伸展臂轴向温度响应曲线与温度场云图Fig.10 Axial temperature response curves and temperature field contours of the deployable mast
不同温度载荷下伸展臂轴向热变形有限元仿真结果与计算结果,如图13 所示。由图13 可见,无论是热传导解析法还是有限元拟合法,计算所得热变形值均略微高于有限元仿真结果。这主要是由于轴向热传导以及空气的热扩散不均匀性所导致,具体误差对比见表4。由表4 得出:热传导解析法计算所得热变形的平均相对误差为3.56%,而有限元推导解方法计算热变形量的平均相对误差为5.26%。有限元拟合法热变形计算误差略大于热传导解析法,表明上述两种热变形计算方法具有较好的热变形反演精度与较强的工程适用性。
6 结束语
本文针对空间伸展臂热属性监测需求,研究了一种基于分布式光纤传感器的铝合金方形管伸展臂模型温度、热应变和热变形测量技术。
1)以方形管伸展臂结构为研究对象,提出了基于有限元拟合与热传导理论的两类伸展臂轴向热变形计算方法。
2)利用ANSYS Workbench 仿真软件,构建单端热加载模型,得到伸展臂沿轴温度、热应变与热变形分布特征,为分布式光纤传感器传感网络优化配置提供了依据。

图11 伸展臂轴向热应变-温度变化曲线Fig.11 Axial thermal strain-temperature curves of the deployable mast
3)通过在伸展臂结构轴向布置的若干离散FBG 温度传感器与FBG 应变传感器,实时采集结构温度、应变分布以及变化信息,进而反演出结构轴向温度场与应变场。基于热传导理论解析法与有限元拟合法两种计算方法反演所得结构轴向热变形平均相对误差分别为3.556%、5.256%,验证了两种热变形计算方法的可行性。
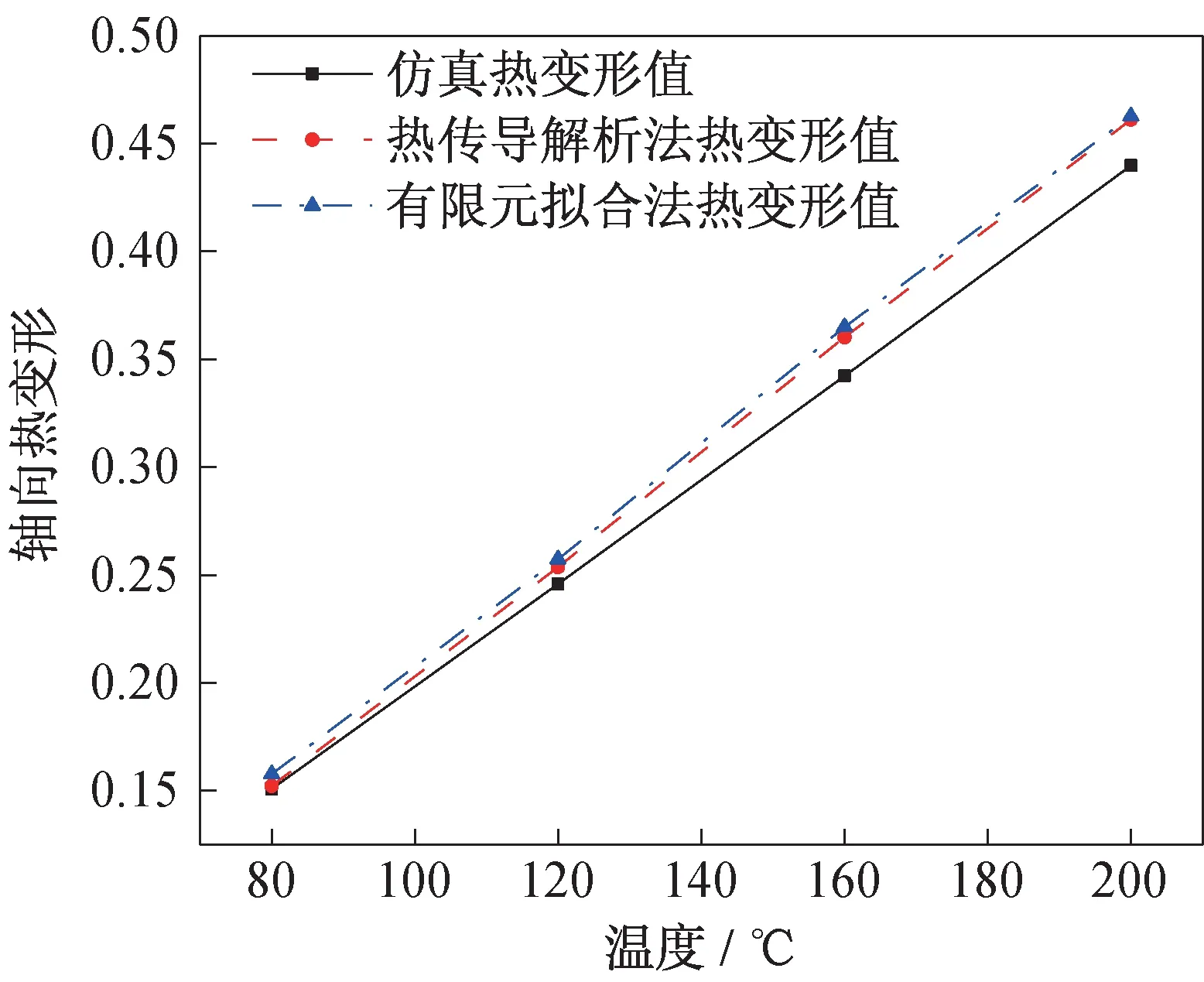
图13 伸展臂轴向热变形计算结果对比Fig.13 Comparison of the calculation results of the axial thermal deformation of the deployable mast
4)本文所提方法具有非视觉测量、实时性好以及多功能集成监测等优点,能够为在轨实时准确获取空间伸展臂结构热属性参数,实现空间伸展臂结构健康监测与形态自适应调节提供有力保障。
5)后续将分别开展针对不同位置或多源热载荷同时加载,以及三维复杂航天器结构温度、热应变与热变形等多物理参量的分布式光纤传感器集成在线监测与反演技术研究。

表3 不同温度下伸展臂轴向热变形计算值与有限元仿真结果对比Tab.3 Comparison of the calculated and simulated values of the axial thermal deformation of the deployable mast at different temperatures

表4 不同温度下伸展臂轴向热变形仿真值与计算值误差对比Tab.4 Error comparison between simulation and test values of the axial thermal deformation of the deployable mast at different temperatures
