改进LMS的光谱信号去噪算法

郑国梁, 朱红求, 李勇刚

中南大学自动化学院, 湖南 长沙 410083

引 言

微型光谱仪是一种利用光的色散原理研制出的光学仪器， 实现对物质浓度和成分的定量和定性分析， 具有检测精度高、 速度快、 非接触等优点[1]。 在利用微型光谱仪对高浓度比背景下多种痕量重金属离子浓度的检测时， 由于离子之间化学特性相近， 导致不同离子之间的原始光谱信号存在一定的重叠[3]。 然而， 多种痕量重金属离子的光谱信号幅值相对于高浓度锌的光谱信号幅值微小， 极容易受到外部环境噪声(包括光源发射功率的不稳定而引起的照射光幅值的波动以及电源、 地线带来的噪声)和内部电路引起的噪声(包括静电感应、 电磁感应以及漏电流感应而仪器的噪声)的干扰[4]， 这些噪声种类多、 来源广且随机性强， 给有效光谱信号的提取和高浓度比背景下多种痕量重金属离子浓度的检测带来了极大的困难。

如何有效的从信号中消除噪声， 针对具体的应用场景， 目前国内外学者已经进行了许多研究工作。 文献[5]中利用Savitzky-Golay (SG)去噪算法对遥感领域中的高光谱数据进行降噪分析； 文献[6]作者设计了一个收缩因子， 能够正确区分高频系数中包含的噪声系数和信息系数。 文献[7]提出了一种新的自适应阈值函数去噪法， 改进了传统的软硬阈值函数， 提升了去噪效果； 但其阈值函数较复杂， 不适用于工程实践。

基于梯度下降法发展起来的最小均方(least mean square, LMS)自适应滤波算法[8]是依据最小均方误差准则来不断修正滤波器系数从而达到去噪目的的算法。 该算法能够在无先验知识的条件下， 通过与外部环境的接触不断修正模型参数从而提高对信号处理性能， 在许多需要对信号进行滤波处理的领域上有着广泛的应用[9]。 然而， 标准LMS算法在对数据进行去噪处理过程中， 存在着对噪声信号敏感、 收敛速度慢、 易出现过拟合的问题。 因此， 本工作提出了一种基于sigmoid误差约束的改进型LMS自适应去噪算法。 首先对标准LMS算法原理进行分析， 并结合微型光谱仪的数据干扰影响情况对标准LMS滤波器结构进行优化改进； 利用sigmoid函数具有误差约束的特性， 将误差计算模块进行优化改进； 由于改进后的最小均方误差损失函数是一个非凸函数、 求解过程容易陷入局部最优解的问题， 为此， 提出一种类交叉熵损失函数， 将非凸出数转化为了一个凸优化问题， 保证了局部最优解也是全局最优解， 同时结合Adam算法来自适应的调整学习率因子； 结合实验数据利用交叉验证的方法选择最佳参数。 最后， 通过交叉验证的方法对所提方法进行实验验证。

1 LMS算法原理及改进

1.1 标准LMS算法原理

LMS算法是依据最小均方误差准则， 采用梯度下降的方法来实现损失函数最小化的去噪算法。 如图1所示， 该算法结构主要由滤波器结构、 误差计算模块、 LMS自适应滤波算法结构组成。 滤波器结构如式(1)所示：

y(n)=W(n)TX(n)

(1)

其中，X(n)=[x(n)，x(n-1)， …，x(n-L+1)]T， 表示与n对应的自适应滤波器的输入信号矢量；y(n)表示n对应的滤波器输出信号；L代表该滤波器的阶数；W(n)=[w0(n)，w1(n)， …，wL-1(n)]T， 表示n状态下的自适应滤波器权系数向量。

误差计算模块通常用式(2)进行表示：

e(n)=y(n)-s(n)

(2)

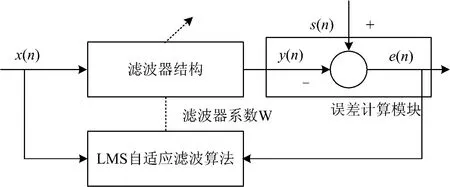
图1 LMS算法结构

其中，s表示n对应的参考输入信号； LMS自适应滤波算法结构是采用最小均方误差函数作为优化的目标函数。 因此， 可以用式(3)描述：

(3)

其中,W=[w0，w1，…，wL-1]。 将式(2)代入式(3)， 用式(4)进行描述：

(4)

利用梯度下降逐步最小化损失函数， 标准LMS算法迭代方程可用式(5)描述：

(5)

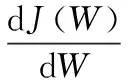
1.2 改进型LMS算法

由式(1)可知， 标准LMS算法是根据前L个输入数据点来对当前数据点进行预测。 微型光谱仪常采用的是电荷耦合器件(charge coupled device, CCD)作为感光组件， 实现光信号转换为数字信号[11]。 CCD感光组件是通过一系列排列在一起的感光像元矩阵单元组成， 如图2所示。 当一束平行光照射至感光像元矩阵单元， 所有的感光像元同时采集信号。 若将所有的感光像元进行有序编号， 图2中x(n-m)位置的感光像元受到的干扰不仅来自于A+方向的反射光、 散射光、 杂散光的干扰影响， 同时也来自A-方向的干扰影响， 而式(1)只能实现对A+方向的消噪。 因此， 对式(1)进行优化改进， 用式(6)描述：

(6)

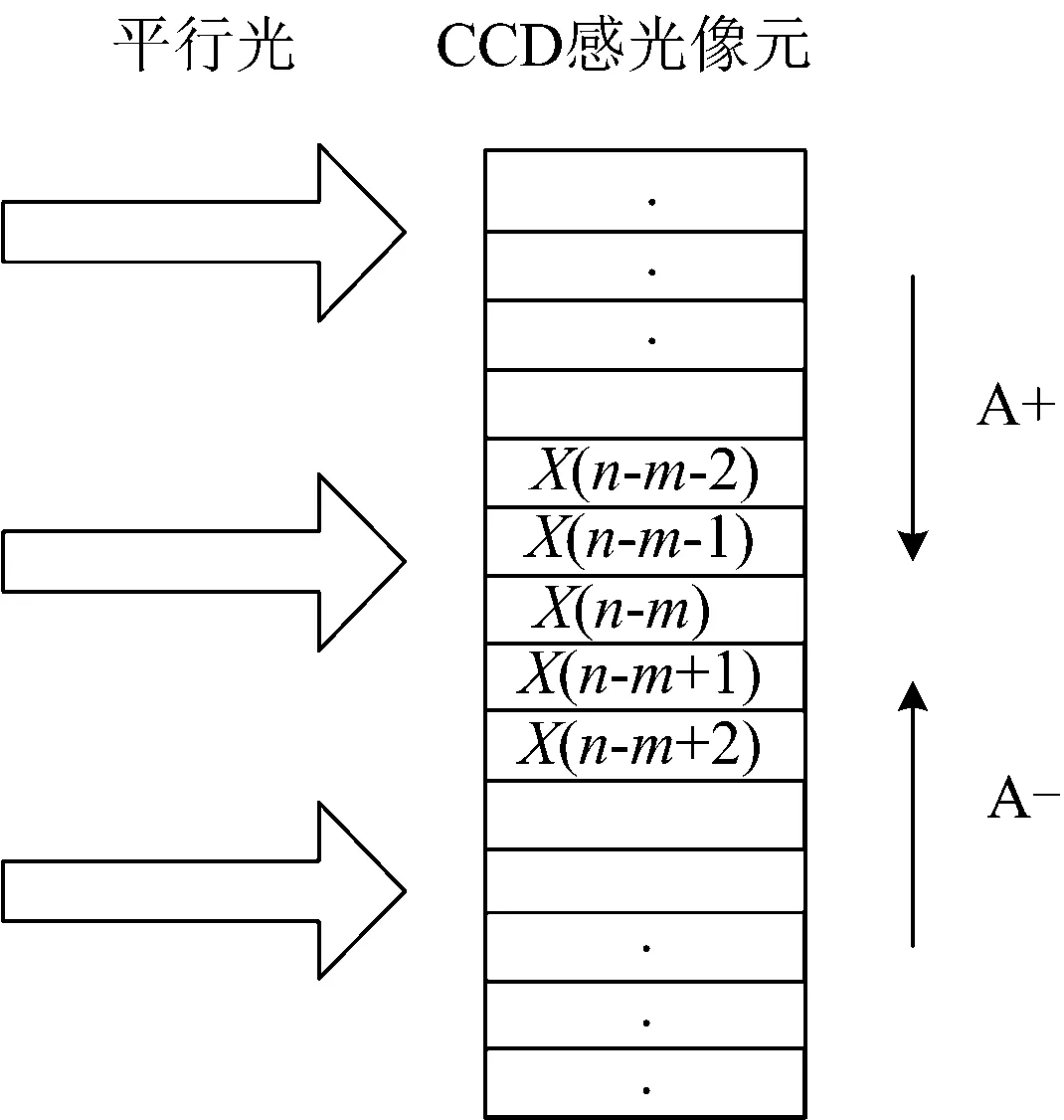
图2 CCD采光原理

利用式(2)计算误差的过程中， 仅利用训练样本中的一个样本来进行误差计算， 将导致对噪声信号比较敏感， 且容易陷入局部最优解中， 当噪声信号过大时， 则计算得到的偏差非常大， 利用式(5)进行权系数向量W迭代的过程中， 权系数向量值变化剧烈， 导致收敛时间变长， 甚至让整个算法模型处于不收敛状态。 为了避免该情况发生， 采用小批量随机梯度下降法[12]更新迭代权系数向量W， 同时为了避免算法对噪声信号的过度敏感性， 用式(7)对式(2)进行改写：

(7)

利用sigmoid函数将噪声信号引起的偏差量约束到-0.5至0.5之间， 如图3所示， 在某种程度上减低了算法模型对噪声信号的敏感性， 同时在进行权值更新迭代时， 自适应滤波器的权系数向量权值变化不会处于震荡状态， 有利于权值系数的快速收敛。

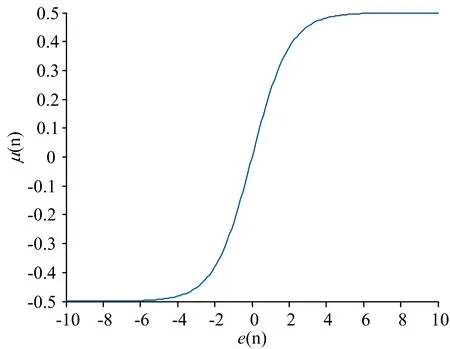
图3 误差约束

将式(7)代入由小批量随机梯度下降法建立起的最小均方误差函数， 用式(8)进行描述：

(8)

其中，k表示随机采样且用于模型训练的样本数量。 利用参数辨识的过程中， 式(8)是一个非凸函数， 存在许多局部最优解[13]， 避免局部最优解的干扰。 将式(8)中的μ(n)进行改进， 用式(9)进行描述：

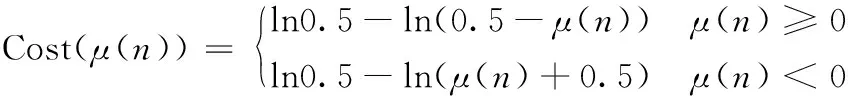
(9)

将式(9)代入式(8)， 然后用式(10)进行描述， 将其称为类交叉熵损失函数。 如图4所示， 将式(8)中的非凸问题转换为了一个凸问题， 在进行参数寻优的过程中， 有效地保证局部最优解也是全局最优解。

(ln0.5-ln(μ(n)(i)+0.5)))2

(10)

利用式(10)对样本数据进行模型迭代训练， 若算法模型选择了更多的参数、 更复杂的模型， 则意味着算法对样本训练数据处理非常好(J(W)≈0)。 但是这样获得的模型丧失了一般性， 从而导致在一个新给定的环境中处理未知样本数据的过程中存在处理效果差的情况。 为了让模型具有较高的泛化能力和抗噪能力， 通常采用正则化的方式对式(10)进行参数约束, 用式(11)对式(10)进行进一步优化改写。

(11)

其中，λ表示正则化系数。 当λ值过大时， 模型将处于欠拟合状态， 当λ值过小时， 模型将处于过拟合状态； 当λ>0时， 能够保证最小化损失函数是一个强凸函数。 将式(11)代入式(5)中进行更新迭代求解最优Wbest， 但是式(5)中的学习率因子α仍然为固定值， 为了不让α成为影响算法收敛速度的主要因素， 需要采用合适的算法来实时调整学习率因子。

图4 误差与损失函数之间的关系

1.3 优化求解

采用自适应矩估计(adaptive moment estimation, Adam)算法来实时调整对应的学习率因子α。 Adam算法[14]根据目标损失函数中每个参数的梯度的一阶矩估计和二阶矩估计动态调整针对每个参数的学习速率因子。 其中， Adam也是基于梯度下降的方法， 每次迭代参数的学习步长都有一个确定的范围， 不会因为很大的梯度而导致很大的学习步长， 保证参数的值比较稳定。 具体程序流程图如图5所示。

根据图5的算法步骤求解出最优W， 但是算法中依然存在超参数滤波器阶数m和正则化系数λ的选择； 采用交叉验证的方法找最佳超参数mbest,λbest。 首先， 将样本按照比例为70%, 15%和15%随机划分为训练集、 验证集和测试集， 其中训练样本用于训练模型， 验证样本用于检验和评价训练样本获得的模型性能， 并根据模型性能优劣来选择最优超参数mbest,λbest； 然后， 利用已选择mbest,λbest并结合训练样本和验证样本来再次训练改进型LMS算法模型获得最优Wbest； 最后， 利用测试样本来测试获得的模型性能。 采用信噪比(signal noise ratio, SNR)和均方误差(mean squared error, MSE)作为模型性能优劣的选择标准。

图5 Adam流程图

2 实验结果与讨论

为了验证所提方法的可行性和正确性， 选择厦门奥普天成有限公司生产型号为ATP2000的便携式微型光谱仪作实验， 光源采用氘卤灯， 比色皿选择石英比色皿。

2.1 数据获取

以锌湿法冶炼为背景， 配置Zn2+， Cu2+， Co2+， Ni2+浓度分别为16 g·L-1， 1.4 mg·L-1， 0.8 mg·L-1， 0.3 mg·L-1的混合标准溶液。 微型光谱仪采样积分时间设定为3 ms， 采样积分间隔为500 ms， 在相同实验条件下将该浓度的光谱信号重复采集4 000次。 图6(a)为其中一次采样获得的吸收光谱信号。 图6(b)是根据中心极限定理统计获得的吸收光谱信号， 在此作为参考吸收光谱信号。

2.2 仿真验证

为了验证方法的有效性和正确性， 选择MATALB2016b作为实验仿真平台。 首先选择图6(b)中的标准参考吸收光谱信号进行仿真实验验证， 选择matlab软件中函数名为awgn的函数， 获取添加高斯白噪后信噪比SNR=[8， 8.08， 8.16， …， 26]的仿真数据， 单位为dB， 总样本量为226。 如图7为信噪比为16.32 dB的光谱含噪仿真信号。 为了让算法模型具有较强的实用性， 在样本划分过程中， 将含噪的仿真数据进行归一化处理， 然后进行模型训练。 对图5中初始化值进行以下设定：

k=20;λ=[0.001, 0.005, 0.01, 0.1, 1, 2, 3, 6, 9, 15, 20];m=[3, 5, …, 29]; 最大迭代次数Tmax=300。

根据图5的程序步骤和交叉验证的方法对模型进行迭代求解， 同时独立重复100次实验验证。

图6 混合溶液的吸收光谱信号

为了进一步验证本方法的降噪效果， 选择标准LMS算法、 小波硬阈值去噪算法、 小波软阈值去噪算法、 SG去噪算法与本方法进行性能比较。 其中标准LMS算法参数设定为：α=[0.000 5， 0.000 1， 5.0×10-5, 1.0×10-5， 5.0×10-6， 1.0×10-6， 5.0×10-7， 1.0×10-7]；L=[3， 5， …， 30]； 选择连续性和对称性较好的”sym8”作为小波基函数， 并进行3层分解； SG滤波器窗口宽度选择3， 多项式拟合次数选择1次。

选择相同的测试集样本来评价这5种不同算法的性能， 如图8所示的均方误差和信噪比这两项性能指标进行统计计算， 本文所提出的改进型LMS算法相对于标准LMS算法、 SG去噪算法、 小波软阈值、 小波硬阈值去噪算法， 信噪比分别提高了9.225%， 19.678%， 7.591%， 12.042%； 均方误差分别降低了59.647%， 63.070%， 53.600%， 57.793%； 有效地说明了本方法的正确性和可行性。

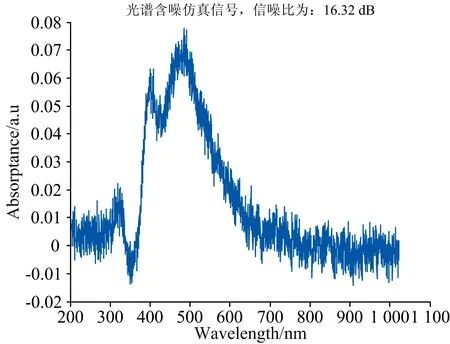
图7 信噪比为16.32 dB的光谱含噪仿真信号

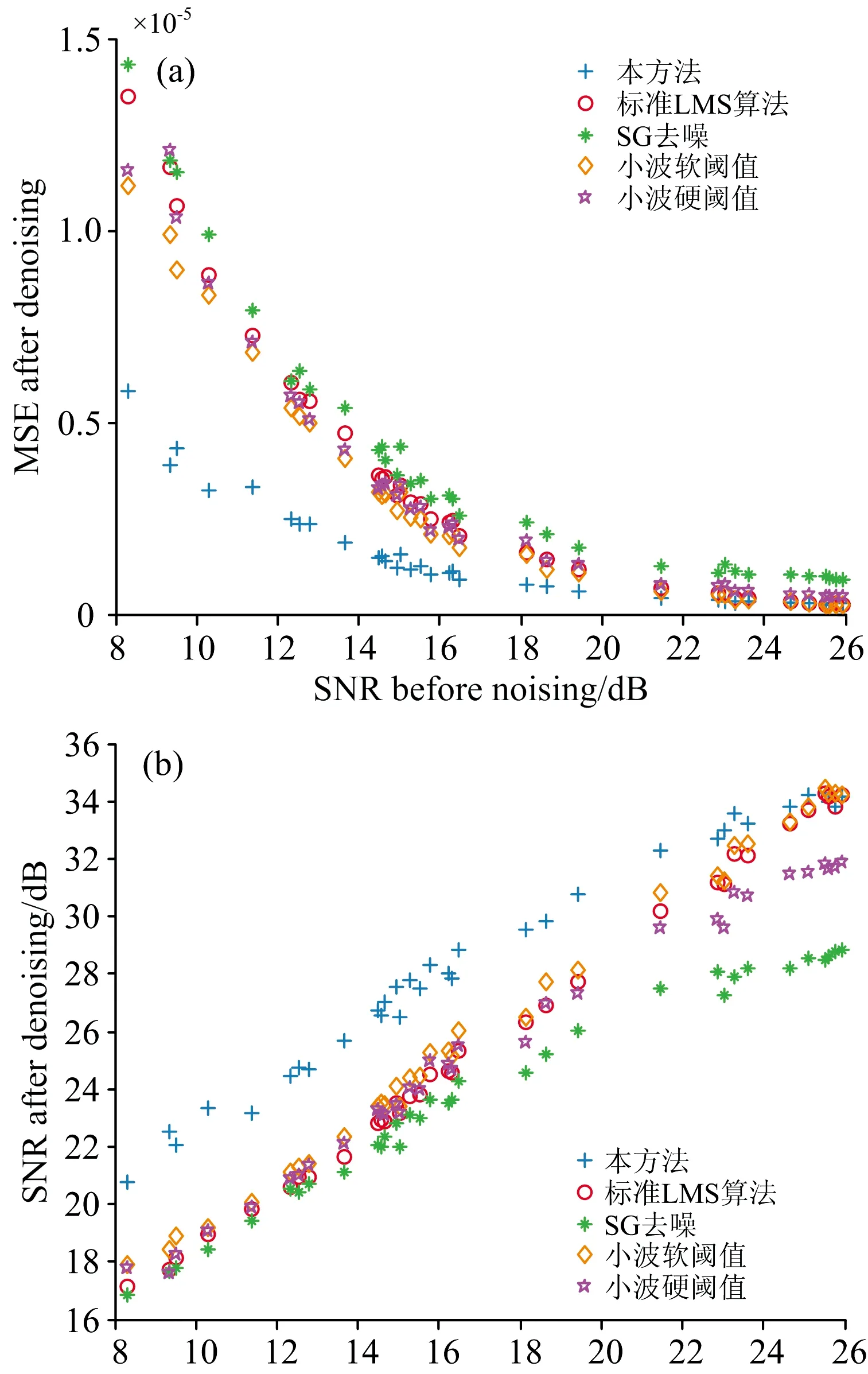
图8 不同算法性能指标对比

以图7中信噪比为16.32 dB的含噪仿真数据为例， 利用上述5种滤波去噪算法进行滤波处理， 去噪效果如图9—图13所示； 观察虚线框中的去噪后的信号， 改进后的LMS滤波算法能够较为真实的还原了原始信号的数据特征， 其他4种方法进行去噪后仍然存在较大的毛刺， 在某种程度上影响着光谱分析精度。

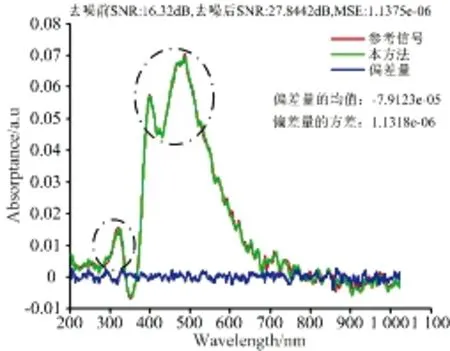
图9 改进LMS算法对仿真数据降噪效果

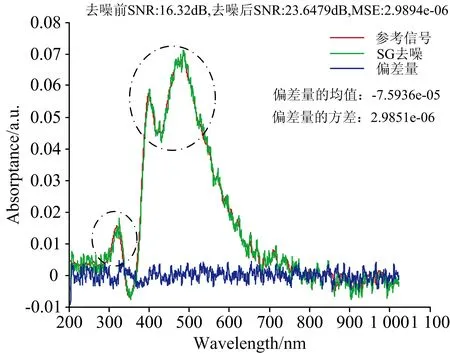
图10 SG算法对仿真数据降噪效果

图11 小波硬阈值算法对仿真数据降噪效果

2.3 实测光谱信号验证

利用本方法对微型光谱仪实测吸光度光谱信号进行去噪处理， 去噪效果如图14所示， 改进型LMS算法有效的消除了强噪声的干扰， 同时也有效的保留了高浓度比背景下多种痕量重金属离子的原始吸收光度图谱信号特征。

图12 小波软阈值算法对仿真数据降噪效果

图13 标准LMS算法对仿真数据降噪效果

图14 改进LMS算法对实测光谱数据降噪效果

3 结 论

微型光谱仪检测高浓度比背景下多种痕量重金属离子浓度的光谱吸收信号存在噪声信号大的问题， 通过对标准LMS算法原理和微型光谱仪的数据干扰影响情况进行了分析， 提出了一种基于sigmoid误差约束的改进型LMS自适应去噪算法， 有效降低了标准LMS算法对噪声的敏感性。 针对改进后的最小均方误差损失函数是一个非凸函数的问题， 本工作提出了一种类交叉熵损失函数， 将非凸问题转化为了一个凸优化问题， 并结合Adam算法来自适应的调整学习率因子， 保证了算法具有较快的收敛速度。 最后结合仿真实验和实测实验进行分析对比。 其结果表明： 对处理信噪比低的吸收光谱信号过程中， 所提方法在信噪比和均方误差的性能指标均优于标准LMS算法、 SG去噪算法、 小波软阈值算法、 小波硬阈值算法， 不仅有效去除无关噪声的影响， 保留光谱信号中的一些重要真实细节特征， 而且也避免了关键细节参数需要依靠主观判断选择的问题， 为分析低信噪比下的光谱信号提供了一种新的解决思路。