水下爆炸冲击波数值仿真研究

胡亮亮，黄瑞源，李世超，秦 健，王金相，荣 光

（1南京理工大学瞬态物理国家重点实验室，江苏 南京 210094；2海军研究院，北京 100161）

水下爆炸历来都是各国关注的重要研究项目。在军事上，水下爆炸是水中兵器设计技术、破坏效应和水下爆破工程的基础问题；在民用工业上，挖凿河道、破暗礁开航道以及爆炸成型等也都涉及到水下爆炸。因此，研究水下爆炸对军事[1]和民用工业[2]都具有十分重要的现实意义。

目前关于水下爆炸的研究方法有理论研究、实验研究和数值仿真。对于理论研究，水下爆炸过程非常复杂，只有少数问题存在解析解。对于实验研究[3-6]，水下爆炸实验周期长、耗费多、成功率低，且所获得的数据有限。近年来，随着计算机性能的迅速提高和数值仿真的深入发展，水下爆炸冲击响应的数值仿真[7-9]越来越受到重视。通过数值仿真，不仅可以减少实验工作量，而且还可以模拟分析实验无法达到的环境条件，获得很多实验无法测得的数据，把研究工作做得更深入、更系统、更完善。

水下爆炸对目标物的毁伤分为近距接触爆炸与远距非接触爆炸，其中爆破开凿河道、水下兵器破坏效应等近距接触爆炸，主要是通过水下爆炸冲击波和气泡脉动耦合作用使目标物产生严重破坏[10]；而在水下远距非接触爆炸中，主要是水下爆炸产生的冲击波对远距离目标物进行毁伤，因此冲击波产生和传播过程一直是抗爆防护研究的重点。冲击波的峰值压力与比冲量作为衡量冲击波毁伤威力的重要指标，对其进行相关研究具有重要意义。对于水下爆炸冲击波的数值仿真的研究，如何提高数值仿真的精度一直是学者们探讨的热点。徐豫新等[11]对Autodyn程序中常用的水的两种状态方程进行了分析，通过对比采用不同状态方程得到的峰值压力计算结果，讨论了两种状态方程的优缺点。刘科种等[12]通过TNT一维轴对称楔形计算模型，分析了人工黏性系数对水下冲击波压力衰减的影响。方斌等[13]采用Dytran程序分析了50 kg炸药水下爆炸情况下网格密度对仿真结果的影响。此外，还有其他学者[14-15]对影响水下爆炸计算精度的因素进行了研究，但缺少三者因素对冲击波峰值压力与比冲量计算结果影响的详细探讨。本研究以常规TNT炸药的水下爆炸为例，系统地对水的状态方程、人工黏性系数和网格尺寸大小这3个主要影响因素进行探讨，从而探寻这些因素对水下爆炸冲击波数值仿真的影响规律，为提高不同工况下水下爆炸冲击波数值仿真精度提供借鉴，从而为较远距离水下爆炸冲击响应数值仿真提供一定的指导。

1 状态方程与参数设置

TNT炸药状态方程采用标准的JWL状态方程，具体形式为

式中：η=ρ/ρ0；A、B、ω、R1、R2为常数，取值如表1 所示。

表1 TNT炸药的主要参数[16]Table 1 Main parameters of TNT explosives[16]

1.1 水的状态方程

1.1.1 Mie-Grüneisen状态方程

目前对于水下爆炸数值仿真，众多学者[17-18]采用Mie-Grüneisen状态方程，该状态方程形式为

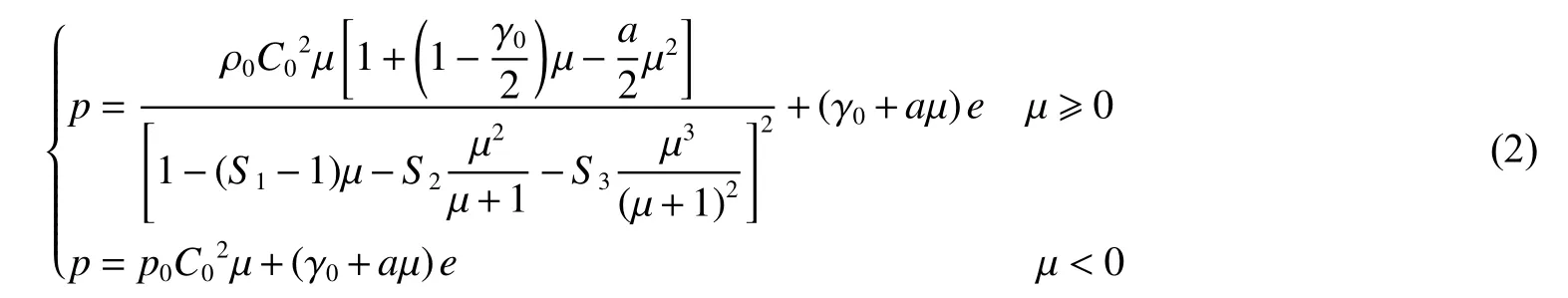
式中：μ为压缩比，μ=η-1。当μ＞0时，水处于压缩状态；当μ＜0时，水处于膨胀状态。C0为声速，γ0为Mie-Grüneisen系数，a为体积修正系数，S1、S2和S3为实验拟合系数。

Mie-Grüneisen状态方程在常用商业软件Msc.Dytran、Abaqus、Autodyn和Ls-Dyna等都运用很广，根据其不同的简化表达式，可得到SNL状态方程、HULL状态方程和Steinberg状态方程[19]等，其参数选取如表2所示。

表2 常用Mie-Grüneisen状态方程不同形式的参数Table 2 Commonly used parameters of the Mie-Grüneisen equation of state

1.1.2 多项式状态方程

多项式形式的状态方程也是常用的水的状态方程，也有许多学者[12,23-24]采用此类状态方程进行水下爆炸数值仿真，并取得了不少的成果。其中Autodyn多项式状态方程的具体形式为

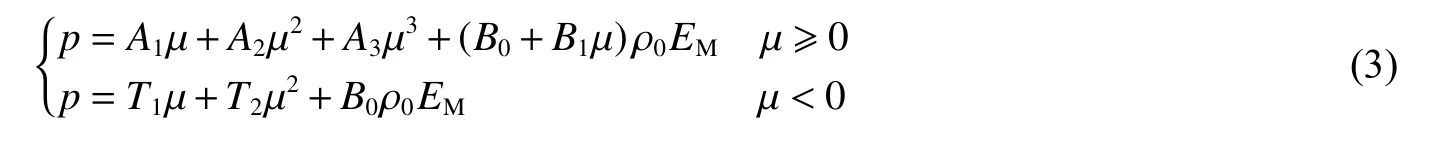
其常用的参数大小如表3所示。

表3 Autodyn程序提供的水多项式状态方程参数[12, 23]Table 3 Polynomial state equation parameters of water provided by the Autodyn program[12, 23]

在Msc.Dytran中多项式形式的具体形式如式(4)，参数如表4所示。

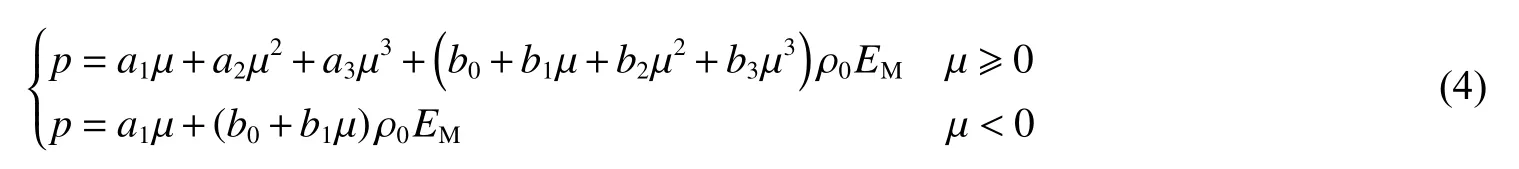
表4 Dytran中水的多项式状态方程的参数[24–25]Table 4 Polynomial state equations parameters of water in Dytran[24–25]

目前关于冲击波在水中的传播，有3种应用较为广泛的冲击波理论[10]，分别是基尔克乌特-别泽理论、基尔克乌特-布林克里理论和宾尼理论，都是根据流体动力学的基本方程式得到的近似解。但是，3种理论的解法和所作假设的物理根据却不同。当距离与药包半径之比大于10时，按基尔克乌特-布林克里理论计算出来的峰值压力与距离的关系曲线和实验值很一致；按基尔克乌特-别泽理论所得到的曲线则比实验值大15%～20%；按宾尼理论所得到的曲线则比实验值要低，但是在药包附近则急剧增加。相对于以上冲击波理论而言，在工程上人们更习惯于使用由相似理论得到的经验公式，而不同学者得到的经验公式却各不相同，其中Cole[26]、Zamyshlyayev[27]等推导得到的经验公式一直被各国水下爆炸研究者引用，本研究也以该经验公式作为数值仿真结果的对比参考，探讨不同条件对数值仿真结果精度的影响，其具体形式如式(5)和式(6)所示

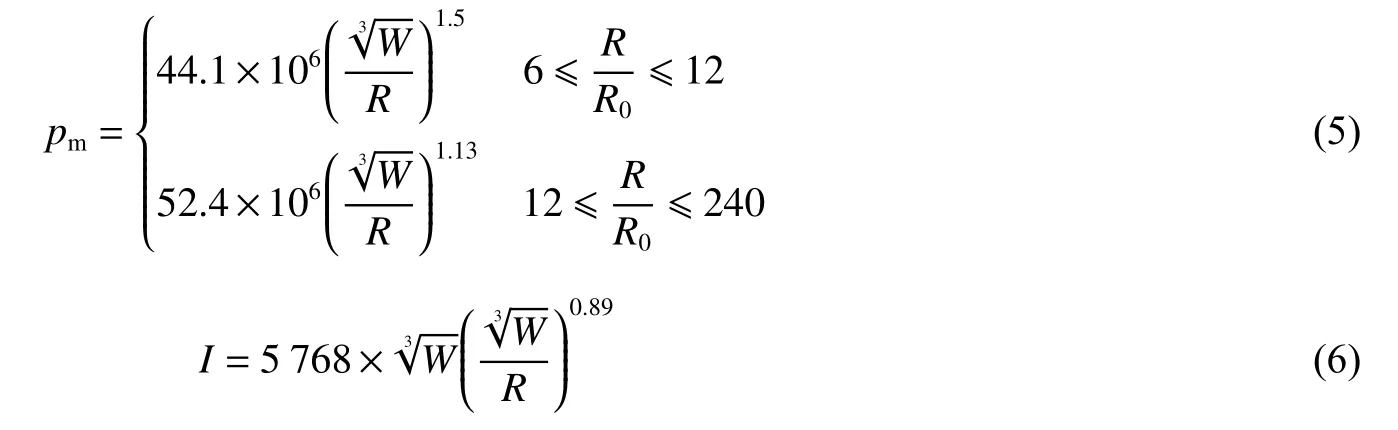
式中：pm为冲击波峰值压力(Pa)，W为炸药质量(kg)，R为爆距(m)，R0为药包半径(m)，I为比冲量(N·s·m-2)。

1.2 水的状态方程对数值仿真结果的影响

关于水的状态方程对数值仿真的影响，有许多学者进行了一系列的讨论。徐豫新等[11]对Autodyn程序中常用的SNL状态方程与多项式状态方程进行了研究，对采用不同状态方程计算得到的峰值压力进行了对比，讨论了这两种状态方程的优缺点。方斌等[13]对Dytran程序中Mie-Grüneisen状态方程与多项式状态方程进行了计算分析，认为它们的计算结果有一定差别。其他学者[20,24]探究了水的状态方程对水下冲击波数值仿真的影响，但缺少状态方程对冲击波比冲量计算结果的影响分析，也没有给出各状态方程在不同比例爆距下的具体误差分析。为深入研究水的状态方程对水下爆炸数值仿真结果的影响，本研究分别采用上述5种常用的状态方程对1 kg TNT在无限水域中的爆炸进行了系列计算，以2 mm的网格划分，监测爆距为7R0、10R0、15R0、20R0、25R0、30R0和35R0的点位，得到了不同状态方程下峰值压力与比冲量的计算结果，与经验公式进行对比，结果如图1和图2所示。

根据计算得到的峰值压力与比冲量，对其进行总结，并结合对比经验公式计算值，如表5和表6所示。

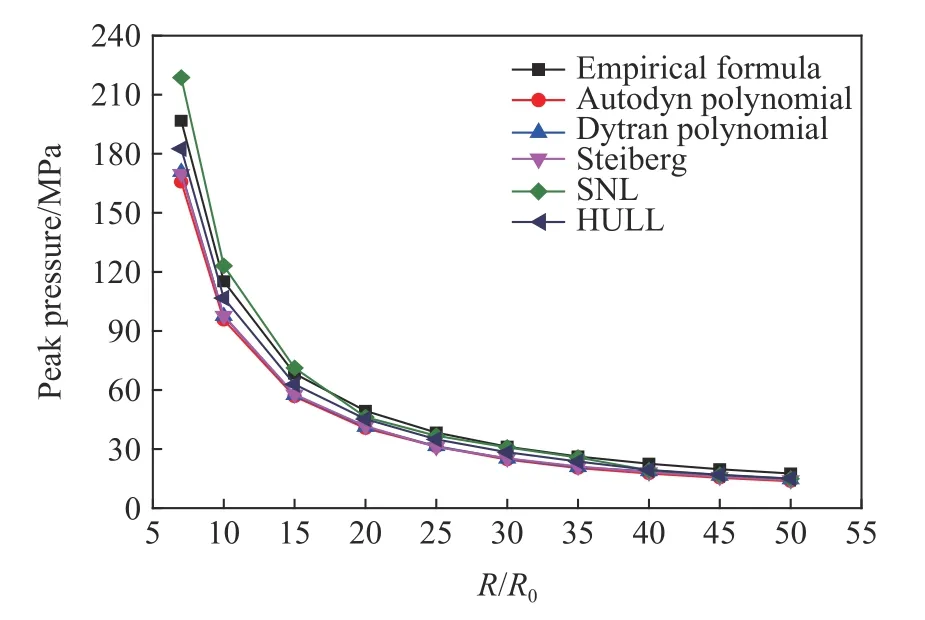
图1 采用不同状态方程得到的峰值压力计算结果Fig.1 Calculated peak pressure results using different equations of states

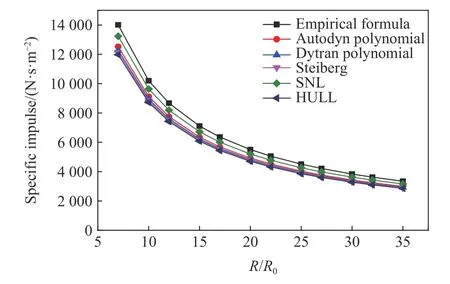
图2 采用不同状态方程得到的比冲量计算结果Fig.2 Calculated specific impulse results obtained with different equations of states

表5 1 kg炸药无限水域爆炸冲击波峰值压力Table 5 Shock wave peak pressure of 1 kg explosive infinite water fields explosion MPa

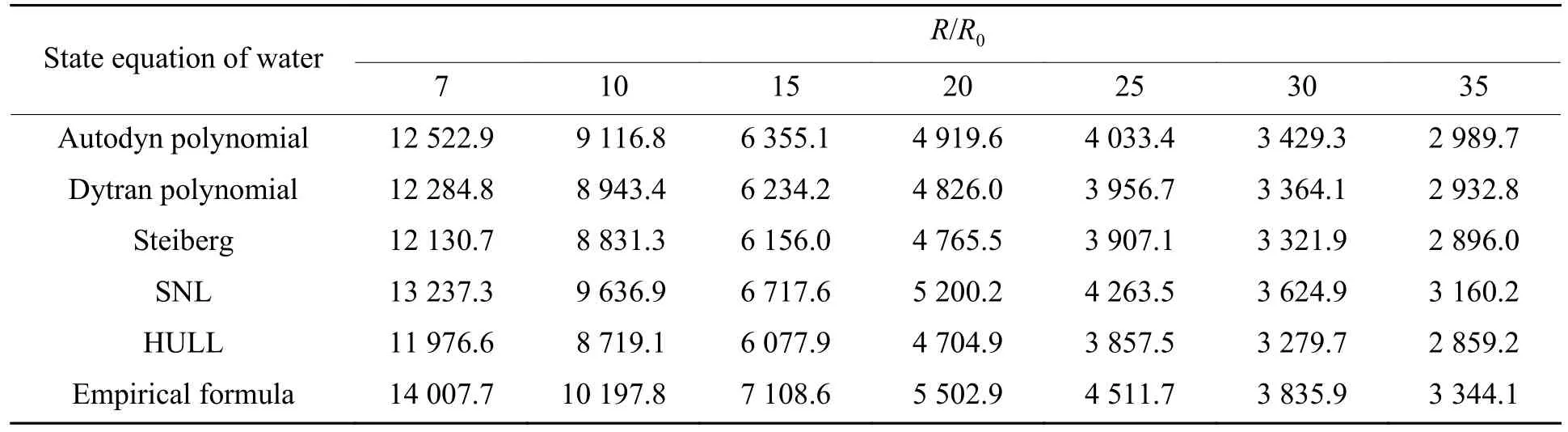
表6 1 kg炸药无限水域爆炸冲击波比冲量Table 6 Shock wave impulse of 1 kg explosives infinite water fields explosion N·s·m-2

结合表5和表6可以看出，这5种状态方程都可以模拟水下冲击波的衰减过程，但每种状态方程衰减的规律不同，从近场到远场的冲击波峰值压力与比冲量计算结果也有所差别，其中采用Autodyn多项式状态方程得到的峰值压力整体误差偏大，远场误差较近场大，比冲量计算结果近场误差较小远场误差较；Dytran多项式与Steiberg状态方程计算结果衰减规律相似，在(10～20)R0爆距处衰减平稳，近场比冲量误差偏大；SNL状态方程近场峰值压力比经验值大，在(7～20)R0爆距区间内衰减较快，远场误差较小，适合进行远场计算[24]；HULL状态方程整体误差较小，近场误差较小，适合进行近场计算。根据不同水的状态方程对计算结果的影响，本节总结了这些状态方程的适用范围与特点，如表7所示。

表7 5种常用水的状态方程的适用范围与特点Table 7 Applicable scope and characteristics of common five kinds of state equations for water

2 人工黏性系数

水下爆炸冲击波波阵面前后压力、密度等会出现突变，这种不连续的状态使得微分方程的求解面临困难，所以计算程序中通常引入人工黏性来解决这一问题，其中一次黏性系数削弱单位最高阶频率中的震荡，二次黏性引入一个阻抗压力来防止单元压溃。但是引入人工黏性会在计算域的几个网格宽度内光滑冲击波阵面，抑制陡峭峰值压力后的尾随振荡，影响冲击波峰值压力的大小。因此，人工黏性系数的选取对于计算结果有较大的影响。

在Autodyn程序中人工黏性一次项、二次项系数默认值为0.2和1.0[28]，人工黏性的形式为

式中：CL为一次项人工黏性系数,CQ为二次项人工黏性系数,l为特征长度,ρ'为材料密度,c为材料中波速,ε为体积变化率。

由于人工黏性系数对计算结果有着明显的影响，许多学者在进行水下爆炸数值仿真时，通过采用调整人工黏性系数来提高数值仿真的精度。徐豫新等[11]在其他计算条件相同的前提下，修改一次项黏性系数0.2为0.16、0.14，修改二次项黏性系数1.0为0.8、0.6进行计算得出冲击波波峰压力衰减的规律，认为通过减少黏性系数，可以提高冲击波峰值压力，使计算结果与经验公式更加接近。杨坤等[29]在控制二次项黏性系数不变的情况下，通过调整一次项黏性系数，分析一次黏性系数对峰值压力的影响。

为了更系统研究人工黏性系数对水下爆炸模拟结果的影响，本节以1 kg TNT炸药在无限水域中的爆炸为例，采用Autodyn程序中的SNL状态方程，并采用2 mm网格进行计算，分别调整一次黏性系数与二次黏性系数，通过与经验公式的计算值对比来研究黏性系数对计算结果的影响。在保持二次项黏性系数为0.9不变的前提下，通过调整一次项系数分别为0.005、0.010、0.020、0.040、0.080、0.200及0.400进行系列计算，监测爆距分别为7R0、10R0、15R0、20R0、25R0、30R0与35R0的点位，得到的计算结果如图3所示。从图3中可以看出，随着一次黏性系数的逐渐减小，峰值压力逐渐增大，近场区受一次项黏性系数的影响较大，并且当一次项系数小于0.040时，近场7R0处的峰值压力跟经验公式计算值的误差为9.43%，已经完全能满足工程精度要求。再通过保持一次项黏性系数为0.02不变，通过调整二次项系数分别为0.5、0.6、0.7、0.8、0.9、1.0，同样监测爆距分别为7R0、10R0、15R0、20R0、25R0、30R0、35R0的点位，得到的计算结果如图4所示。从图4中可以看出，二次黏性系数的改变对计算结果的影响不大，在取值为0.8～1.0时，计算结果与经验公式基本吻合。

本研究也对0.1、10、50和100 kg进行计算分析，发现在不同当量工况下一次与二次黏性系数对于冲击波峰值压力与比冲量影响规律基本与1 kg一致，一次黏性系数对峰值压力影响较大，对比冲量的影响较小，当一次黏性系数增大，冲击波峰值压力减小，衰减更明显；二次黏性系数对峰值压力与比冲量的影响较小。一次黏性系数对不同当量工况的影响情况如图5所示，从图中可以发现，当一次黏性系数在0.005～0.040之间时，不同当量工况下都能满足近远场精度要求。

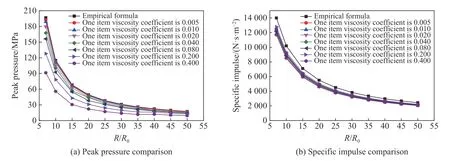
图3 调整一次项黏性系数得到的计算结果Fig.3 Calculated results obtained by adjusting the viscosity coefficient of the primary term

图4 调整二次项黏性系数得到的计算结果Fig.4 Calculated results obtained by adjusting the viscosity coefficient of the quadratic term

图5 一次黏性系数对不同当量工况的影响Fig.5 Effects of primary viscosity coefficient under different equivalent conditions

根据以上对计算结果的分析，本节对人工黏性对水下爆炸冲击波数值仿真计算结果的影响进行总结分析，并给出了一次与二次黏性系数的建议取值范围，如表8所示。

表8 人工黏性对计算结果的影响Table 8 Artificial viscosity effects on calculation results

3 网格尺寸对计算结果的影响

众所周知，网格尺寸对于数值仿真的结果有很大影响，进行数值仿真前一般都要进行网格无关性的验证[30]。对于水下爆炸问题，当计算域较大时很难实现过于细密的网格划分，为了探寻水下爆炸数值仿真中不同工况下的合理网格尺寸，张社荣等[31]对不同当量炸药在无限水域内爆炸的网格尺寸进行了研究，提出了炸药半径与网格尺寸之比为基准的网格划分的方法；余晓菲等[32]采用Msc.Dytran软件研究了50、70 mm等网格尺寸下水下爆炸冲击波峰值压力的计算误差；方斌等[33]对药量为50 kg的水下爆炸情况的网格尺寸影响进行了分析，对网格尺寸大小与峰值压力误差的关系进行了讨论。此外，还有许多学者[34-36]对于水下爆炸冲击波数值仿真中的网格尺寸的选取做了一些研究，但对不同当量的炸药工况采用多大网格尺寸能满足工程精度要求并未进行系统的讨论。本研究拟以冲击波峰值压力和比冲量为衡量标准，通过系列仿真计算并进行总结归纳，从而给出不同当量炸药在数值仿真中满足工程精度要求下的参考适宜网格尺寸。

首先本节以1 kg炸药无限水域爆炸工况为例，分别采用2、5、8、12、15和20 mm网格尺寸进行计算，监测从近场7R0到远场35R0处的冲击波峰值压力与比冲量，得到的计算结果如图6、图7所示，不同网格尺寸下具体的峰值压力与比冲量计算值如表9、表10所示。当采用的网格尺寸逐渐增大时，峰值压力与比冲量相对误差都逐渐增大，并且网格尺寸对于峰值压力的影响较比冲量大，当峰值压力达到精度要求时，比冲量计算结果基本也能达到精度要求。所以本节以峰值压力与经验公式计算值误差小于10%的精度要求为衡量标准，当网格尺寸为5 mm时，已经完全达到精度要求，虽然2 mm网格的计算结果更加精确，但采用2 mm网格需要的计算时间更长、对计算硬件要求更高，在已经满足计算精度要求的情况下，则认为1 kg炸药无限水域爆炸工况下，最佳的适应网格为5 mm。

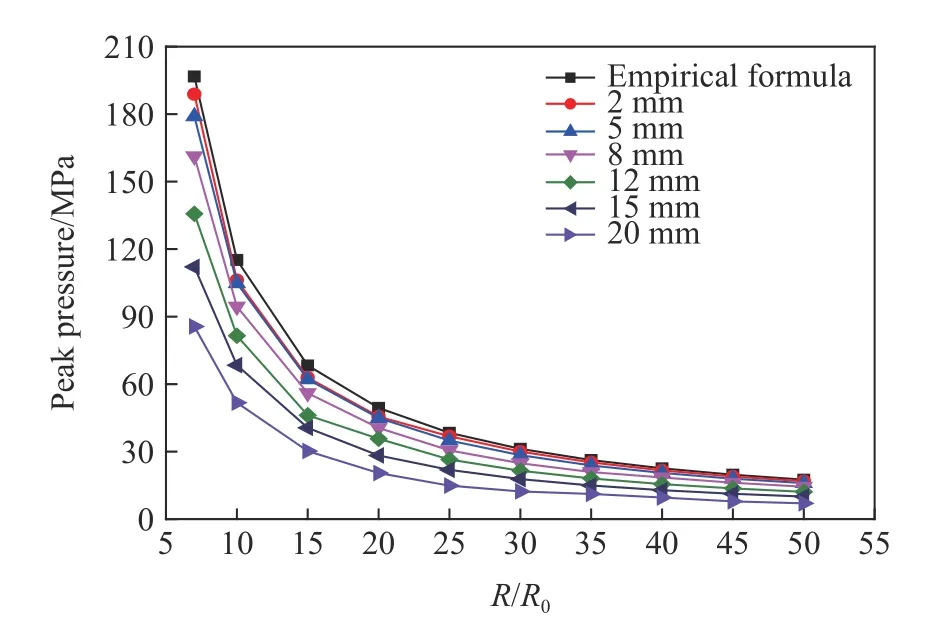
图6 采用不同网格下得到的峰值压力Fig.6 Peak pressure obtained under different grids

图7 采用不同网格下得到的比冲量Fig.7 Specific impulse obtained under different grids

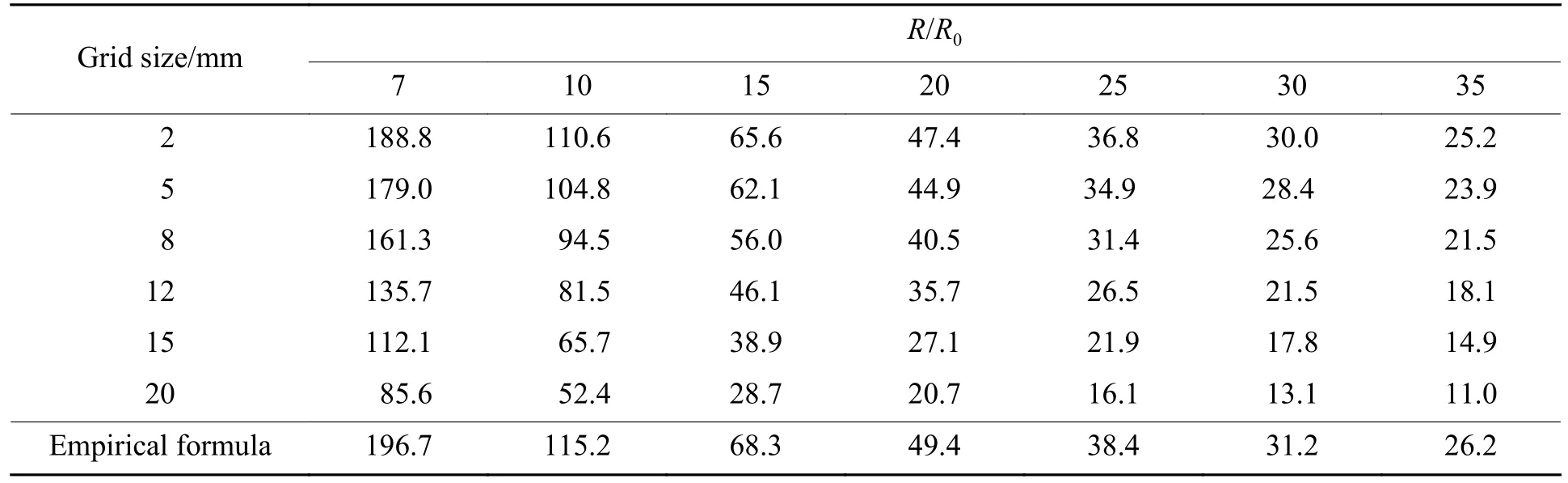
表9 1 kg炸药采用不同网格尺寸得到的峰值压力Table 9 Peak pressure of 1 kg explosive with different grid sizes MPa

表10 1 kg炸药采用不同网格尺寸得到的比冲量Table 10 Specific impulse of 1 kg explosive with different grid sizes N·s·m-2

同样对0.1、0.5、10、50、100、500和1 000 kg不同量级炸药水下爆炸工况进行系列计算，得到峰值压力计算结果如图8所示。并对不同尺寸网格下的得到的峰值压力进行误差分析，同样以峰值压力与经验公式计算值误差小于10%的精度要求为衡量标准，得到了这些当量下分别对应的最佳网格尺寸，如表11所示。

为了定性描述水下爆炸炸药当量W与适宜网格尺寸li之间的表达式，通过分析其他案例中的不同当量工况使用的网格尺寸与得到的精度误差，并结合本研究得到的表11，发现当量与网格尺寸之间呈指数关系，取工况W0=1 kg下的适宜网格尺寸l0=5 mm作为基本量，采用式（8）的方程式进行描述，得到无量纲炸药当量与无量纲适宜网格尺寸之间的关系

拟合图如图9所示，拟合效果良好，并得到材料参数n=0.746、m=0.371，从而为水下爆炸数值仿真中不同炸药当量下网格尺寸的选取提供合理参考。

基于对水的状态方程、人工黏性系数及网格尺寸对于水下爆炸冲击波的数值仿真计算结果精度的影响分析，本研究以三维大水域无限水下爆炸模拟为例，采用Steinberg状态方程对0.1 kg TNT球形炸药水下爆炸模拟，其中炸药和水采用多物质Euler算法，并采用无反射边界条件来模拟无限大水域情况，采用1.5 mm网格尺寸进行数值模拟，分别监测在1、2和3 m处测得到的冲击波时程曲线，得到的仿真结果如图10（a）所示，可以看出数值仿真可以很好地模拟水下冲击波的衰减过程。并通过与尹群[25]在0.1 kg TNT水下爆炸试验测得的3 m处的时程曲线进行了对比，如图10（b）所示，从图中可以看出，数值仿真得到的冲击波时程曲线与试验测得的冲击波时程曲线重合度很好，验证了文中对于提高水下爆炸冲击波数值仿真精度的探讨的有效性，从而为水下爆炸数值仿真提供有益的借鉴。

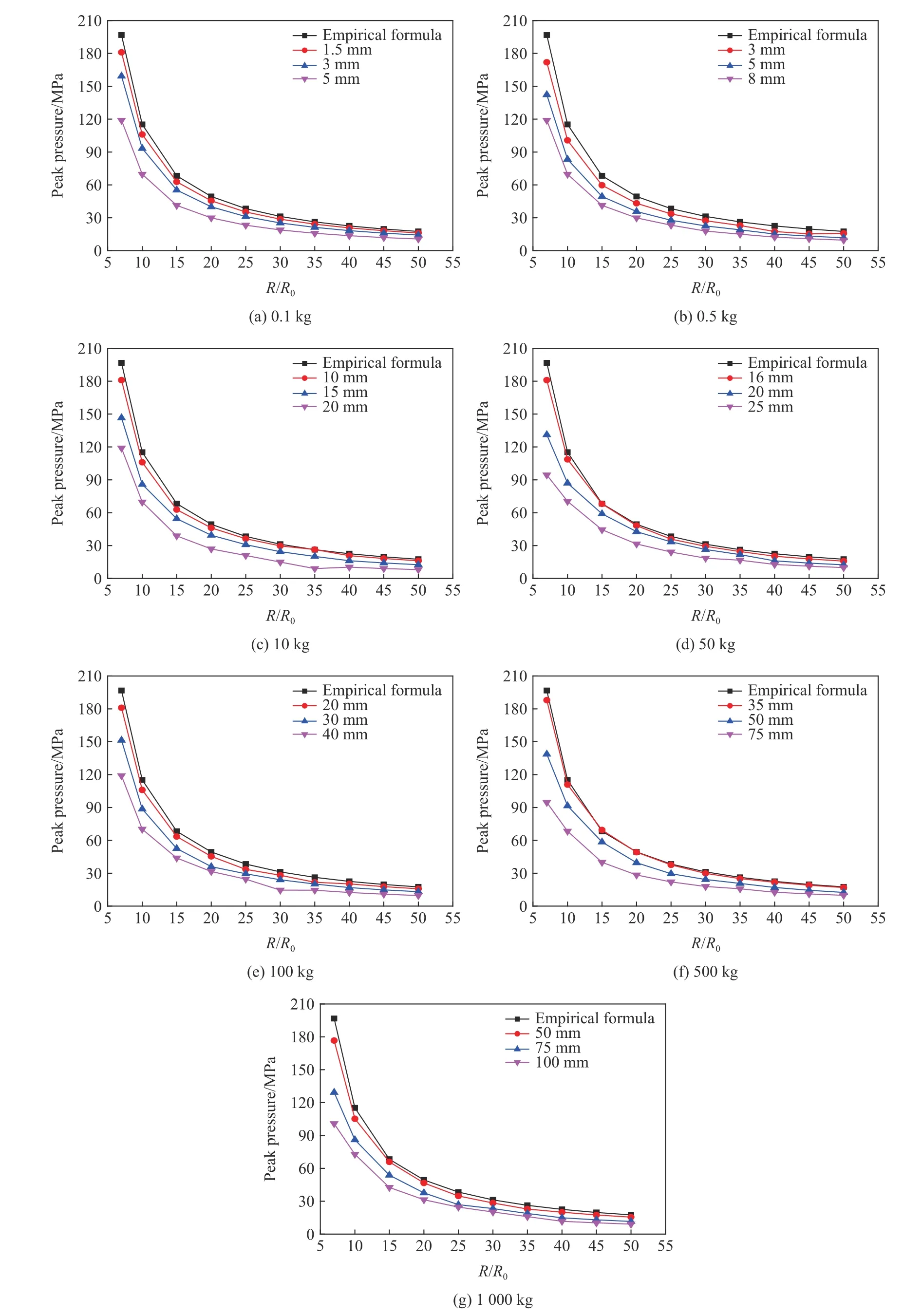
图8 网格尺寸对不同炸药当量水下爆炸数值仿真的影响Fig.8 Influence of grid size on different explosive equivalents numerical simulation of underwater explosion

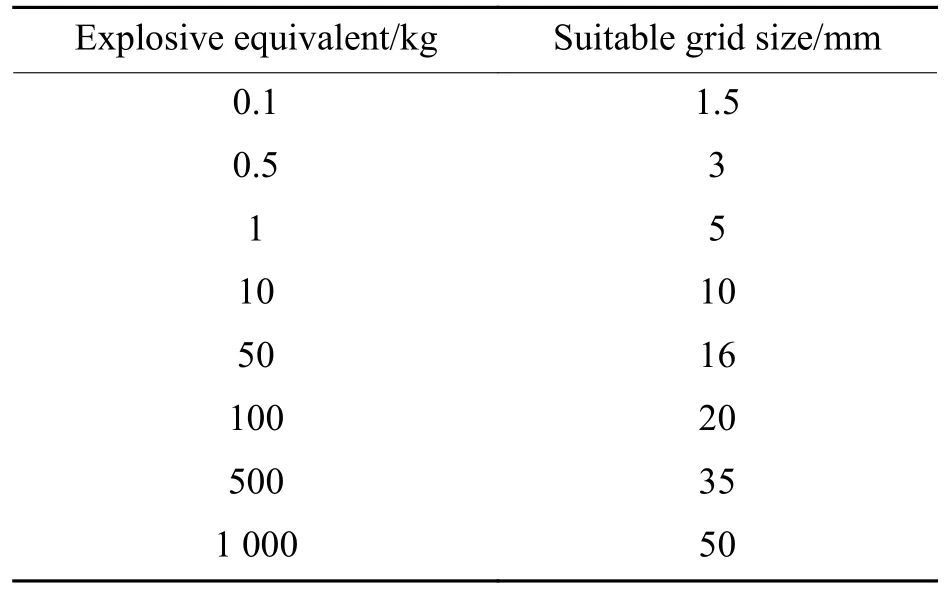
表11 不同炸药当量下适宜网格尺寸Table 11 Appropriate grid size for different explosive equivalents

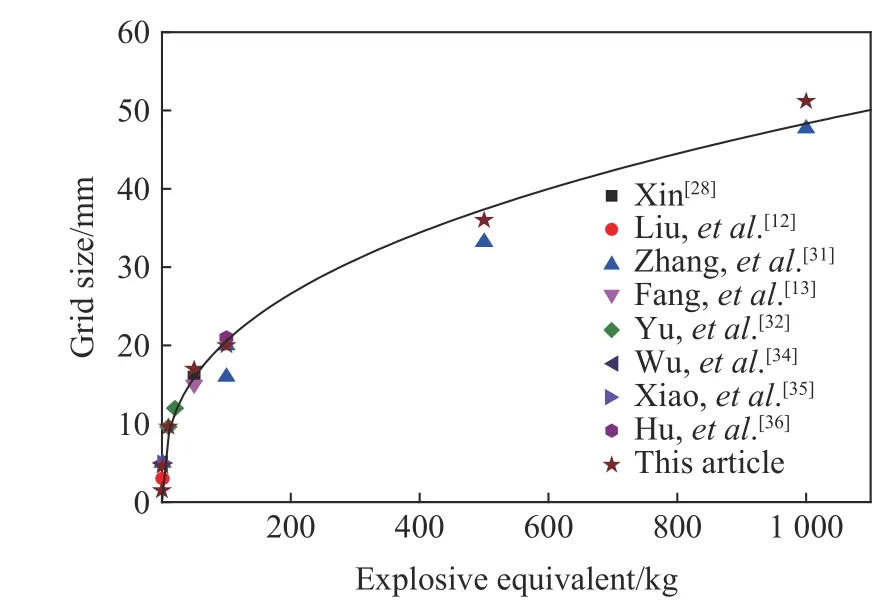
图9 炸药当量与适宜网格尺寸的关系Fig.9 Relationship between explosive equivalent and suitable grid size

图10 数值仿真得到的冲击波时程曲线与试验对比Fig.10 Numerical and experimental comparison of shock wave time history curve

4 结 论

针对水下远距非接触爆炸情况，以常规TNT炸药在水下爆炸冲击波中的数值仿真为例，采用冲击波的峰值压力与比冲量为衡量毁伤威力的指标，通过系列仿真并结合计算结果与经验公式的对比，分析了水的状态方程、人工黏性系数及网格尺寸对水下爆炸冲击波的数值仿真计算结果的影响。

（1）分别采用5种常用状态方程进行计算，对得到的水下冲击波峰值压力与比冲量的计算结果进行误差分析，得到了采用不同水的状态方程计算下的近远场峰值压力与比冲量相对误差，给出了这5种状态方程的特点与适用范围。

（2）通过系列仿真讨论了一次与二次人工黏性系数对水下数值仿真的影响，发现一次黏性系数对峰值压力的影响较大，对比冲量的影响较小，而二次人工黏性系数对计算结果影响较小。当一次黏性系数增大时，冲击波峰值压力减小，衰减加快。当一次黏性系数取值在0.005～0.040时，冲击波峰值压力误差较小，能满足精度要求。

（3）对不同量级当量炸药水下爆炸进行系列数值仿真，分析了网格尺寸对水下爆炸冲击波峰值压力与比冲量的影响，其中网格尺寸对峰值压力的影响较大，对比冲量的影响较小。并以峰值压力的相对误差小于10%为基准，得到了炸药当量对应的适宜网格尺寸，对其进行了无量纲下的定性分析。