柱状装药预制破片缩比战斗部爆炸冲击波和破片的作用时序

夏冰寒，王金相，周 楠，陈兴旺，卢孚嘉

（1南京理工大学瞬态物理国家重点实验室，江苏 南京 210094；2南京森林警察学院，江苏 南京 210023；3北京北方车辆集团有限公司，北京 100072）

带壳装药战斗部爆炸时，产生空气冲击波的同时，还伴随着大量的高速弹片，共同对目标产生破坏作用。在早期研究该类战斗部的毁伤效果时，通常在远距离处只考虑破片的作用，而在近距离处将其解耦成近场冲击波的作用和高速破片群的作用[1-2]。近年来，国内外学者开始对破片和冲击波的联合毁伤效应展开了研究。Nyström等[3]研究了爆炸产生的冲击波和破片对混凝土的毁伤效果，分别对破片、冲击波的单独作用和联合作用展开分析，得到了联合作用毁伤效果大于两者单独作用毁伤效果的结论。Leppänen[4]利用试验和数值模拟方法研究了破片和冲击波对混凝土的联合毁伤作用，分析了破片密度、炸药量和起爆方式对毁伤的影响，得出的结论为破片和冲击波联合作用下的毁伤大于两种毁伤元单独作用时的毁伤。国内学者张成亮等[5]、李茂等[6]、侯海量等[7]开展了预制破片战斗部对一些组合防护结构的毁伤特性研究，分析了高速破片和爆炸冲击波对不同结构破坏模式的影响，结果表明，高速破片和冲击波的联合作用会加剧目标结构的破坏。

由于冲击波与破片的运动规律大不相同，因此在不同的距离下战斗部爆炸产生的破片和冲击波作用在目标上的先后顺序也不同。确定冲击波与破片同时到达的距离，是研究两种毁伤效应耦合的重要基础。对于破片冲击波的作用时序问题，国内外学者均有研究，Nyström等[3]模拟了炸弹爆炸后破片和冲击波的相遇位置，从而对破片和冲击波的协同作用进行研究。Lloyd[8]分析了导弹战斗部爆炸后不同时间破片相对于冲击波的位置。梁为民等[9]在模拟爆腔内完成了模拟弹对目标靶板的爆炸破坏效应试验，研究了战斗部在结构内爆炸条件下破片和冲击波的运动演化过程，分析了不同比例距离和装药系数下，破片与冲击波的运动规律。安振涛等[10]对破片和冲击波的运动时序问题进行了理论分析，得出了冲击波和破片同时到达目标的距离，该距离大小与破片形状和单个破片质量关系不大。在对冲击波和破片的作用时序问题研究中，通常采用理论计算、数值仿真和试验等方式开展[9-13]。考虑到对于某些较大型战斗部，在仿真计算时会出现网格过多、计算时间过长的问题，实验研究时对实验场地要求很高，且操作困难，耗资较大，因此有必要进行缩比模型的相似律研究。目前相关的研究报道较少，且主要针对冲击波和目标结构的缩比，对于缩比战斗部爆炸产生的破片和冲击波的运动规律，尤其是两者作用时序的规律研究还不够充分。

针对柱状装药预制破片缩比战斗部爆炸产生的破片和冲击波的传播过程与作用时序展开探究，考虑到实验难度较大，各项测量难以实施，故采用量纲分析方法，结合爆炸驱动理论与现有经验公式，对影响破片和冲击波作用时序的因素及其缩比后的相似准则进行分析，确定影响破片和冲击波相遇位置的关键参数，并结合数值模拟结果验证并分析战斗部缩比比例对破片和冲击波作用时序的影响。

1 理论分析

1.1 量纲分析

建立如图1所示的柱状装药预制破片战斗部模型，模型由炸药和破片2部分组成。炸药采用柱状TNT炸药，轴向密集排布540枚扇形破片，破片材料均为45钢，战斗部整体模型如图1(a)所示，其截面如图1(b)所示，其中r、h、d分别为装药半径、装药高度和破片厚度。由于炸药爆炸所产生的能量中破片的变形能约占总能量的1%[10]，因此破片的变形、破坏和质量损失忽略不计，只考虑破片的动能、爆炸产物的动能和内能。决定破片和冲击波相遇位置的控制参数主要来自3个方面：破片的质量mf，炸药的质量me、装药密度ρe、单位质量炸药释放的化学能Ee、爆炸产物的膨胀指数γe，空气的初始压力pa、初始密度ρa、绝热指数γa。以上物理量的单位与量纲如表1所示。

图1 战斗部模型示意图Fig.1 Schematic diagram of the warhead model

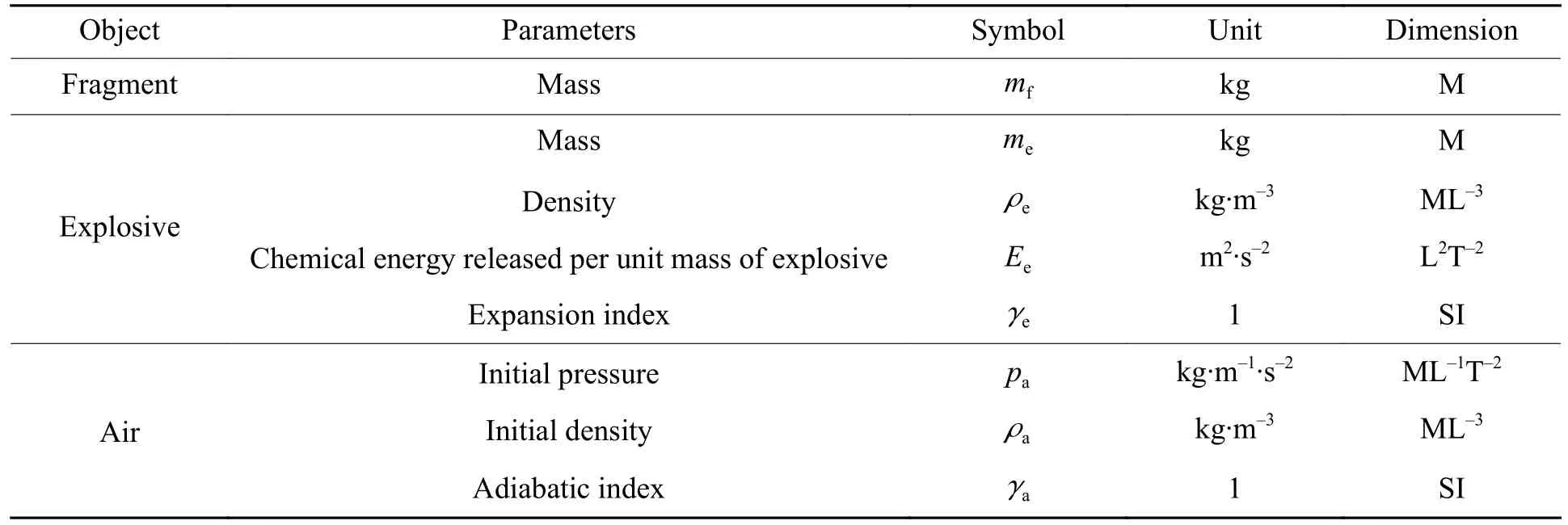
表1 破片和冲击波相遇距离问题中相关物理量及其单位和量纲Table 1 Parameters and their units and dimensions related to the location of the two encounters

若以R表示破片和冲击波的相遇距离，那么存在函数关系式

上述物理量以L、M、T为基本量纲，可取me、ρe、Ee为基本量，则式（1）可化为下面的无量纲关系

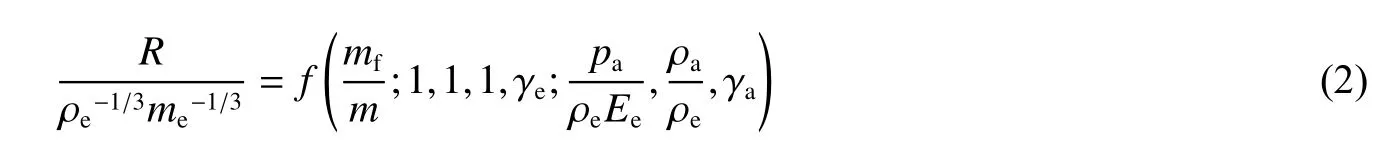
若采用同种炸药在空气中做缩比模型实验，那么有6个有关的控制参数与原模型相同，即

则无量纲函数关系式可简化为

式(4)即为基于量纲分析得到的相遇距离的定性关系式，可知破片和冲击波的相遇距离取决于炸药总质量以及破片和炸药的质量比。

1.2 破片和冲击波相遇位置和相似准则

在1.1节中使用量纲分析法得到的破片和冲击波相遇位置的定性关系式还不足以明确两载荷相遇位置和相关参数的具体关系，本节将结合爆炸驱动理论和相关经验公式对其具体形式进行推导。

对破片，依据Gurney公式[9]可知最大破片速度

式中：G为炸药的格林参数；α为战斗部破片总质量与装药量之比，对于同一战斗部的不同缩比模型，模型中的α应为常数。故不同模型中的破片速度应相等。

考虑到破片的速度衰减，破片飞行时间tf与距离R的关系为[10]

对冲击波，由于破片的存在会在一定程度上削减冲击波的强度，依据能量法可以得到削减后的等效TNT当量mbe与装药时的TNT药量m的关系[10]

式中：β为战斗部的装填系数式(7)可改写为

对于指定的战斗部，由于各缩比模型的α相等，故µ为常数。

冲击波波阵面传播到距离R处的时刻ts可由经验公式[9]改进得到

要求得破片和冲击波同时到达的距离R，令tf=ts，可得

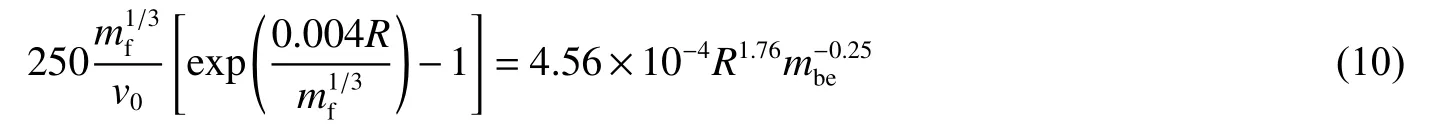
通过式（10）直接求出R与m的关系较为困难，由于近场环境下破片速度衰减较小，因此若不考虑破片速度衰减，式（10）可改写为

如前所述，v0为常数，则式（11）可改写为

忽略破片速度衰减，视破片为匀速运动，可以得到破片和冲击波的相遇时间t

前面已指出，同一原型战斗部的不同缩比模型中v0、µ均为常数,而γ为v0的函数，故γ也为常数。那么由式(12)、式(13)可知，破片和冲击波的相遇距离和时间与等效TNT当量的0.33次方成正比。由此可推断出质量为m的缩比模型中破片冲击波相遇时间t1和距离R1与质量M的原模型中破片冲击波相遇时间t2和位置R2的关系为

2 有限元仿真

2.1 缩比模型

为研究不同缩比尺寸下的工况，针对图1所示的战斗部，保持战斗部各部分尺寸（r、h、d）比例不变，对整体战斗部模型进行缩比。结合前文可知，破片和冲击波的相遇距离主要取决于炸药与破片的质量，故按照0.8∶1、0.4∶1、0.3∶1、0.2∶1、0.1∶1的总质量比设计包括原模型在内共6个模型，具体尺寸列于表2。

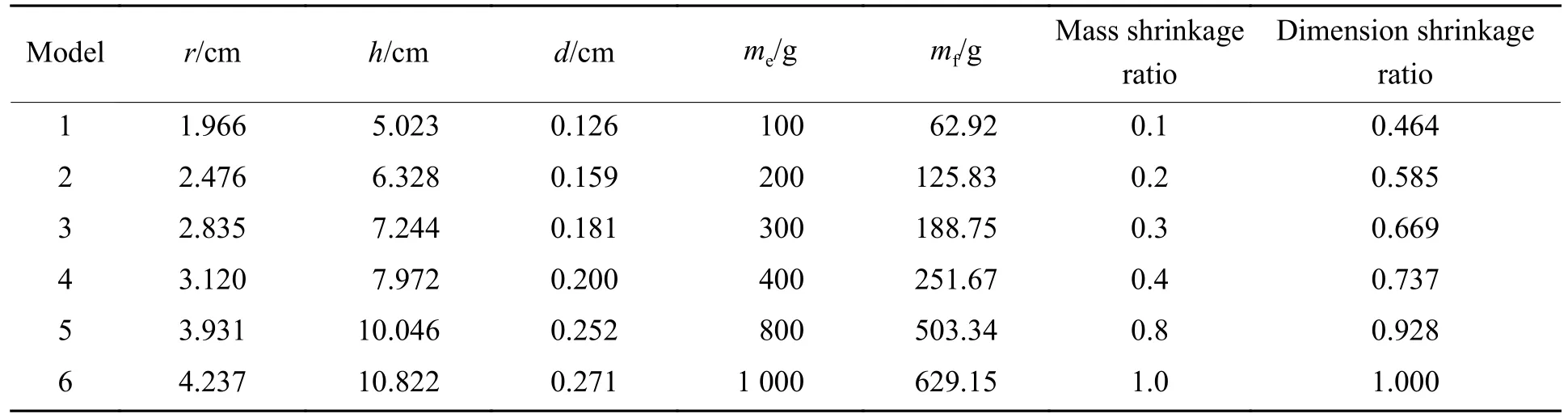
表2 缩比战斗部尺寸Table 2 Scaled warhead size

2.2 有限元模型

采用ANSYS/LS-DYNA非线性动力有限元分析程序，考虑到整体结构的对称性，建立不同缩比质量下的战斗部的1/8模型，如图2所示。

数值模型由炸药、空气和破片3部分组成，均采用8节点Solid164三维实体单元建模，其中炸药、空气单元使用多物质ALE算法，破片采用Lagrange网格建模，破片与炸药和空气材料间采用流固耦合算法。在对称面上设立对称边界，对空气边界设定透射边界。模型采用cm-g-μs单位制。起爆方式为中心线起爆。

炸药采用HIGH_EXPLOSIVE_BURN本构模型，对爆轰产物的膨胀采用JWL状态方程描述

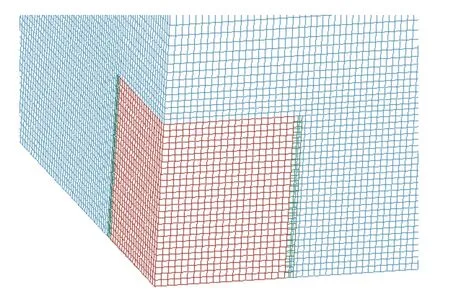
图2 有限元模型Fig.2 Finite element analysis model

式中：p为爆轰压力，A、B、R1、R2、ω为试验确定的参数，e为指定函数，V为相对体积，E为初始内能。计算中所采用的炸药参数见表3[11]。其中，ρ为装药密度，D为爆轰速度，pCJ为爆轰波阵面的压力。

表3 TNT炸药材料参数及JWL状态方程参数Table 3 Parameters of TNT material and JWL equation of state

空气采用NULL材料模型及LINEAR_POLY_NOMIAL状态方程描述

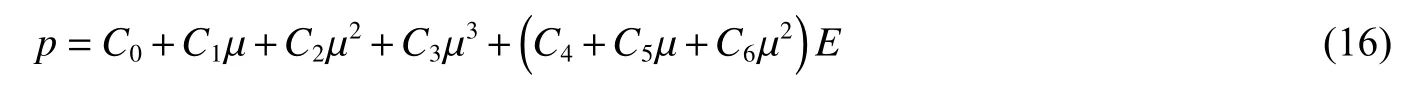
表4 空气材料参数及状态方程参数Table 4 Equation of state parameters of air

破片采用MAT _PLASTIC_KINEMATIC的钢材料模型，其应变率由Cowper-Symonds模型描述

式中：σd为动态屈服强度；σ0为静态屈服强度；E为弹性模量，取E=210 GPa；Eh为硬化模量，取Eh=319 MPa；εp为有效塑性应变；为等效塑性应变率；D、n为常数，对于低碳钢，通常取n=5，D=400 s-1。材料失效模型采用最大等效塑性应变失效准则。破片材料参数见表5[12]，其中ν为泊松比。

表5 破片材料参数及状态方程参数Table 5 Equation of state parameters of fragments

3 结果及分析

3.1 破片和冲击波的传播过程

从各工况的数值仿真结果中可以发现，各个模型中破片和冲击波的传播规律大致相同，图3、图4给出了模型2中各阶段的破片和冲击波传播过程，主要分为4个阶段：第1阶段（Ⅰ）中破片领先于正后方的冲击波，此时冲击波在驱动破片加速的同时绕流过破片；第2阶段（Ⅱ）破片速度趋于平稳，冲击波汇集在破片前方，速度由快至慢衰减；第3阶段（Ⅲ）破片追赶上冲击波；第4阶段（Ⅳ）破片赶超冲击波后领先于冲击波。

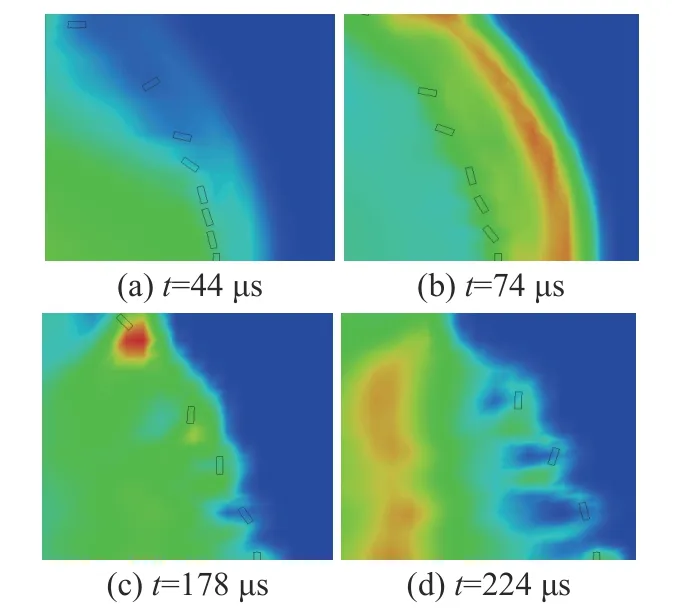
图3 模型2中破片和冲击波的传播Fig.3 Fragmentation and shock wave trajectory in Model 2

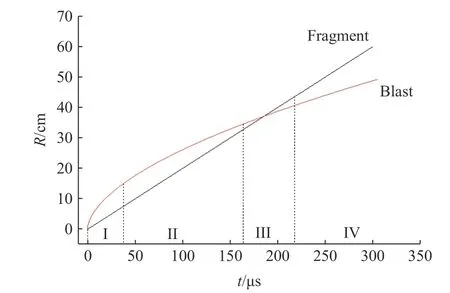
图4 模型2中破片和冲击波的传播距离与时间的关系Fig.4 Propagation of blast wave and fragments as a function of time in air in Model 2

3.2 破片和冲击波的相遇位置

表6给出了各个模型中破片和冲击波的相遇时间、相遇距离与 (m/M)0.33的关系。由表6结果可知，随着模型的减小，破片和冲击波的相遇距离也会随之缩减，这是因为破片的速度保持不变，冲击波速度变小，导致破片追赶上冲击波的时间和距离也随之缩短。对比各结果中的相遇时间缩比、相遇距离缩比与 (m/M)0.33的关系，可以看到，质量缩比在1.0～0.2范围内时，理论与仿真结果符合较好，但误差会随着缩比模型的缩小而增大。这主要是由于在有限元计算中采用的ALE算法考虑了实际的破片和空气的相互作用，而随着模型的缩小，破片迎风面积与质量之比却在增大，因此破片速度衰减带来的影响也越来越大。结合以上数据，可以认为该方法适用于战斗部质量缩比不小于0.2的模型。

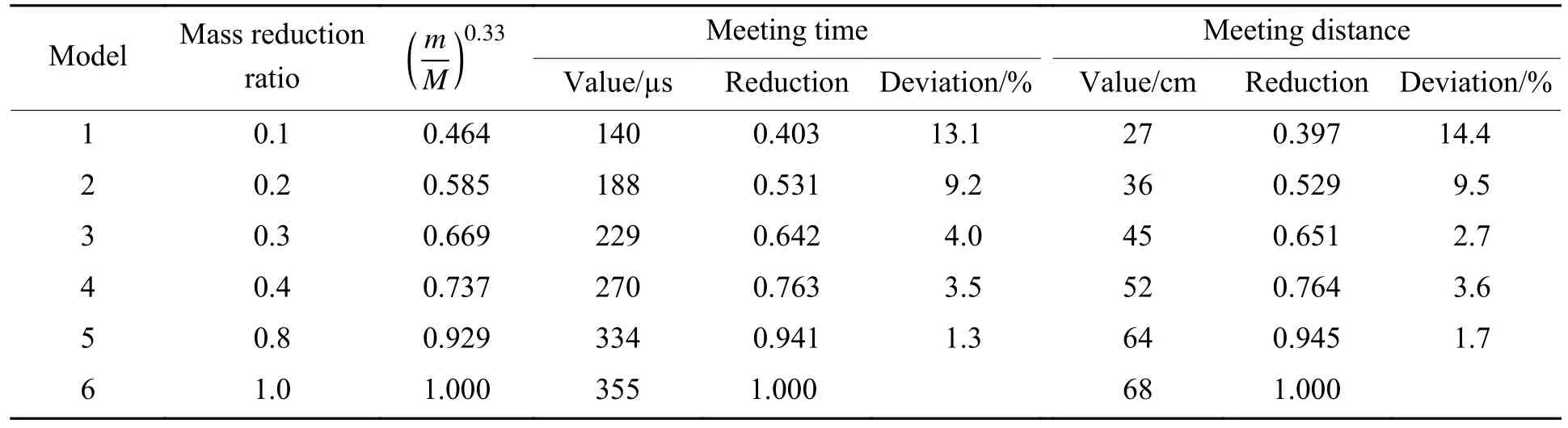
表6 理论结果与仿真结果对比Table 6 Comparison of theoretical and simulation results

4 结 论

缩比模型与原型战斗部爆炸产生的破片和冲击波的相遇位置之比和相遇时间之比取决于两模型的质量比，在不考虑破片速度衰减时，两模型中的相遇位置之比和相遇时间之比等于其质量比的0.33次方。通过有限元仿真验证了理论的有效性，同时由于破片速度衰减的影响，该方法适用于质量缩比不小于0.2的模型。