隧道双层预支护力学分析模型
2020-02-25赵晨阳曹豪荣彭立敏施成华雷明锋杨伟超
赵晨阳,曹豪荣,彭立敏,施成华,雷明锋,2,杨伟超
(1.中南大学土木工程学院,湖南长沙,410075;2.中南大学重载铁路工程结构教育部重点实验室,湖南长沙,410075)
随着基础建设的不断发展,隧道下穿综合管廊、楼房等重要建筑物的案例不断增加,为保证建筑物安全,需同时在结构物附近、开挖轮廓线处采取预支护措施[1]。在富水砂层地区,隧道施工过程中极易发生涌水涌沙等现象,引起地层严重损失。施加管棚、旋喷桩、注浆加固等措施能大幅改良地层性质,控制地下水渗流,有效控制地层沉降变形,在隧道工程领域有着广泛的应用。研究者从多个方面研究了管棚、旋喷桩、注浆等预支护的作用效果与分析模型。在理论分析方面,邢厚俊等[2]将破裂面前方土体与初支结构分别作为管棚支点,建立了简支梁模型;苟德明等[3-5]将整个管棚看作弹性地基梁,土柱荷载作用在已开挖段与破裂面扰动段,考虑支座初始沉降、转角与围岩的黏聚力,建立Pasternak双参数地基梁模型;郑俊杰等[6-7]基于基床系数会随土体性质、应力状态等发生改变的情况,建立了考虑基床系数变化的管棚变形分析模型;周顺华[8]考虑空间荷载效应,认为管棚主要起加固围岩、扩散围岩压力并减少开挖释放应力的作用;贾金青等[9]认为初期支护施作具有一定的滞后性,并建立了考虑滞后效应的地基梁模型。在数值模拟与现场实测方面,伍振志等[10]运用FLAC3D软件分析了管棚注浆加固的效果;张慧乐等[11]基于现场载荷试验与有限元分析方法研究了水平旋喷拱棚结构的承载特性与机理;周前等[12]通过分析认为水平旋喷桩在控制地面沉降与拱顶下沉方面具有良好的效果;CHENG等[13]基于Phase2.0研究了浅埋偏心受压隧道中管棚和锚杆的受力变形机理;董敏等[14]基于3D 模型模拟隧道上台阶开挖全过程,对双层管棚在土层加固效果进行了探讨;SHI 等[15]结合工程实际状况,研究了大长管棚受力变形情况;YANG 等[16]基于Peck理论,揭示了管棚结构变形特性;赵毅鑫等[17]结合超前管棚与注浆措施,研究了联合支护在断层带中的作用;石钰锋等[18]研究了水平旋喷与大管棚联合使用作为初期支护的效果。人们对管棚、水平旋喷桩、注浆等预支护进行了大量研究,但理论研究仅涉及单种预支护方式单层预支护模式的作用效果分析,对多种方式组合情况、考虑层间关系的双层预支护体系协同分析等方面的理论研究仍很少。为此,本文作者结合广佛(广州—佛山)环线城际铁路东平一号隧道工程,考虑管棚、旋喷桩、注浆等多种预加固方式的协同作用,建立隧道双层预支护协同作用的力学分析模型。通过与现场实测数据的对比分析,验证双层预支护模型的可靠性。
1 工程概况
1.1 工程地质概况
广佛环城际铁路东平1号隧道位于佛山市禅城区,下穿岭南大道管廊段(DK18+416.00—DK18+426.80,总长10.80 m)采用暗挖法施工。工点地貌属珠江三角洲海陆交互沉积平原,地形平坦,地面高程-0.50~6.00 m。场地范围内交通便利,各种地下管线(直径为600 mm 和800 mm 雨污、直径为200 mm给水管线)密布,隧道最小埋深10.60 m。综合管廊为钢筋混凝土箱形框架结构,埋深约0.83 m,距隧道开挖轮廓最小距离约4.88 m,实测地下水位在道路路面下-2.40 m,属富水砂质地层。隧道上覆地层主要为杂填土、粉砂、淤泥质粉质黏土,隧道主体结构位于粗砂、粉质黏土和全风化砂岩中,具体地质情况与地层参数分别如图1和表1所示。
1.2 支护方式
结合现场地质、机械设备、工程经济、控制标准等因素,东平1号隧道下穿岭南大道段拟采用双层预支护方式。

图1 暗挖下穿岭南大道地质图Fig.1 Geological map of undermining through Lingnan Street
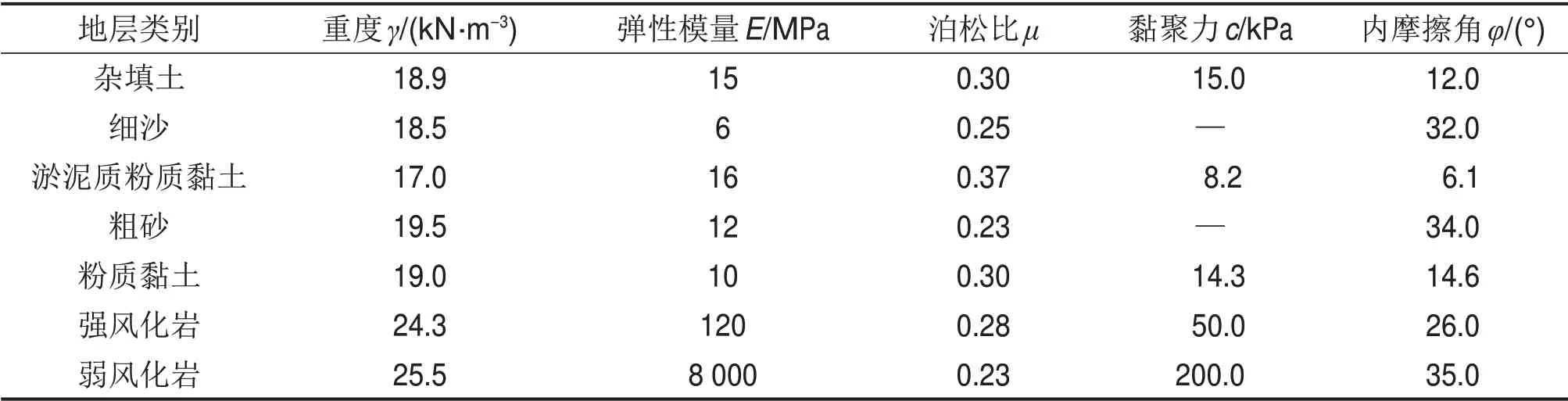
表1 地层参数Table 1 Formation parameters
在隧道两端设置地下连续墙;在距管廊底部和开挖轮廓线外侧约50 cm 处各采用直径为159 mm、间距为500 mm管棚注浆加固,管棚两端利用连续墙进行支撑;广佛江珠左、右线外侧采取2排水平旋喷桩进行封闭止水,开挖轮廓线外部采用1排直径为600 mm、间距为400 mm咬合水平高压旋喷桩;在管廊两侧斜向各施作1 排间距为1 200 mm 的袖阀管,注浆加固管廊下方至隧道拱顶处的土体。预支护方案示意如图2所示。
2 双层超前预支护力学分析模型
2.1 双层预支护体系协同作用分析模型
由于承受的荷载与抗弯刚度不同,上、下层预支护结构的沉降变形存在差异,导致中间土体变形,进一步使得上、下层预支护结构承受的荷载通过土体进行传递,达到协同工作的效果。
根据现场双层预支护施作状况,结合单层管棚支护分析理论[3-5],建立双层预支护体系协同变形分析模型。取隧道开挖纵断面进行分析,将双层预支护等效为双层弹性地基梁,2层预支护之间的围岩视作弹簧,预支护两端的连续墙采用弹性支座进行模拟。其中,AB段模拟喷射混凝土、格栅混凝土衬砌等初期支护完成状态,BC段模拟开挖后未施作初期支护的状态,CD段模拟掌子面前方施工扰动状态,DE段模拟施工未扰动状态。为了更确切地模拟预支护体系的真实受力状况,模型中采用“均布+三角形分布”荷载形式[4-6],即掌子面后方(AC段)为均布荷载,掌子面前方影响范围内(CD段)荷载呈三角形分布,未扰动段(DE段)不计算荷载。预支护体系承受的地基反力作用值采用沉降值与基床系数的乘积。参考文献[12],预支护体系的刚度参数采用管棚、水平旋喷桩与注浆等刚度的等效值。AB段采用预支护体系和初期支护等抗弯刚度的叠加值。两端点(A和E)处采用竖向连杆及水平弹簧进行约束。

图2 预支护措施示意图Fig.2 Schematic diagram of pre-support measures
模型中,记上层预支护体系的挠度为w1,下层预支护体系的挠度为w2;上层预支护体系的抗弯刚度为E1I1,下层预支护体系支护段(AB段)的抗弯刚度为E2I2,其余部分(BZ段)的抗弯刚度为E3I3。在施工过程中,管棚两端(A和E点)连续墙均可能存在沉降,记A端相对于D端的初始沉降为w0,上、下预支护体系之间的地基弹簧刚度为k,CE段地基系数为k0。图3所示为施工纵断面图,图4所示为分析模型。

图3 隧道施工纵断面图Fig.3 Longitudinal section of tunnel construction

图4 隧道双层预支护体系力学分析模型Fig.4 Mechanical analysis model for double layered pre-support system in tunnel
2.2 理论分析计算
根据图4所示双层预支护分析模型,建立梁体单元分段耦合挠曲微分方程组如下。
AB段:
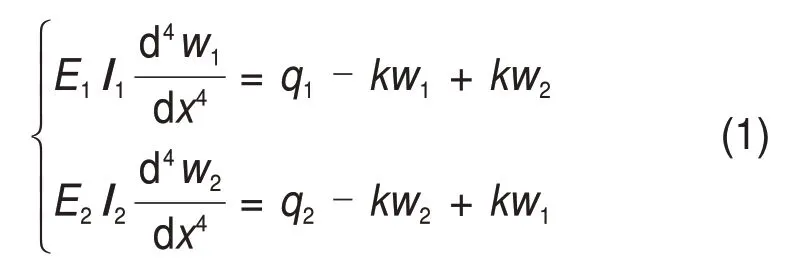
BC段:

CD段:

DE段:

对耦合挠曲微分方程组求解,得到各段方程的解如下。
AB段:

式中:A1~A8为待定系数;
BC段:

式中:B1~B8为待定系数;
CD段:

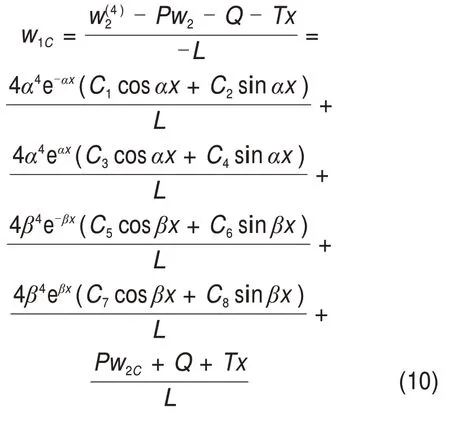
式中:C1~C8为待定系数;

DE段:

式中:D1~D8为待定系数。
根据A和E端支座的下沉与转角,B,C和D点挠曲各阶导数的连续性条件,可列出方程组求解各段挠度方程的待定系数,确定梁体单元各段的挠曲方程。
3 计算结果与分析
3.1 计算参数
水平旋喷桩、注浆体的弹性模量取值参考文献[11-12,17]。中间土体弹簧刚度取注浆区土体的弹性模量,下层土体弹簧刚度采用经验值[19]。
隧道暗挖下穿岭南大道段最小埋深10.60 m,为浅埋隧道,预支护体系承受的荷载可取上方全部土体重度,即上层预支护结构承受其上方土体荷载,下层预支护结构承受上、下层预支护结构中间的土体荷载。根据现场量测数据,隧道起始端地下连续墙的初始沉降约0.50 mm,无转角。
隧道最大分部开挖高度约4.40 m,砂的内摩擦角φ为34°。破裂面是土体发生破坏时形成的滑切面。参考文献[3],根据破裂面的范围计算掌子面前方受扰动土体的范围,CD段长度l计算公式为

计算得l=2.34 m。出于施工安全考虑,取l=2.50 m。
结合隧道设计资料,汇总双层预支护体系分析模型计算参数,如表2所示。

表2 双层预支护模型主要计算参数Table 2 Main calculation parameters of double layered pre-support model
3.2 计算模型验证
为证明施工阶段综合管廊沉降符合模型分析结果,检验理论模型的可靠性,选取广佛(广州—佛山)江珠右线拱顶处预支护结构纵向中点为验证点,如图5中点Z所示。将该测点沉降的理论分析值、实测值与数值模拟值等进行对比。

图5 有限元模型Fig.5 Finite element models
数值模型中,预支护体系的参数取值参考文献[11-12,17]确定,如表3所示。

表3 预支护参数Table 3 Perimeter of pre-support
模型中,开挖洞室位于广佛江珠右线。隧道总长10.80 m。模型共12 个分析步,第1 步为地应力平衡,后续依次为开挖和支护模拟,分11 次进行。前10次单次模拟开挖长度为1.00 m,最后1次模拟开挖长度为0.80 m。通过求解计算,得到双层预支护体系在隧道开挖后的变形状况,如图5所示。
绘制测点挠度随掌子面推进的变化状况,如图6所示。由图6可以看出:测点的挠度理论分析值与实际测量值基本吻合,同时存在一些偏差。
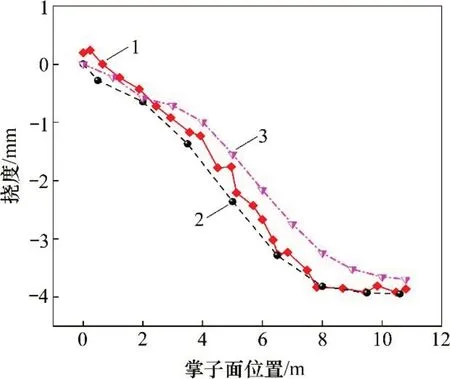
图6 测点沉降随掌子面的变化Fig.6 Settlement of monitoring point changes with tunnel face positions
1)测点挠度的有限元模拟结果与理论分析结果、实测结果呈现相同的变化状态,挠度均随着掌子面的推进不断增加,当掌子面为0~8.0 m时,挠度变化较快;在隧道开挖后期(8.0~10.8 m),挠度基本趋于稳定。
2)测点挠度的理论分析结果、实测结果与有限元分析结果存在偏差。在隧道开挖前期(0~5.0 m),测点挠度的有限元模拟结果与实测结果吻合程度较高。在隧道开挖完成阶段,该点挠度的有限元模拟结果与实测结果发生较大偏差,实测结果为-3.9 mm,数值模拟结果为-3.7 mm,理论分析结果为-4.0 mm。数值模拟结果与实测结果相对误差约5.1%,与理论分析结果相对误差约7.5%,理论结果与实测结果相对误差为2.5%,在可接受范围内,说明理论分析模型具有一定的可靠性。
3.3 计算结果与分析
根据表2,对双层预支护体系挠曲变形随掌子面推进的变化状况进行分析。体系挠度曲线如图7所示,其中,不同的曲线代表掌子面处于相应位置时整个预支护结构的变形,如1 m代表掌子面处于距隧道起点1 m位置时整个预支护结构的挠曲变形状况。

图7 预支护体系在不同掌子面位置的挠度Fig.7 Deflections of pre-support system at different tunnel face positions
由图7可知:
1)随着掌子面的推进,上、下层预支护结构的挠度均呈现增大状态;当隧道开挖完成时,上层预支护结构挠度最大值约为3.9 mm,满足综合管廊内部管线沉降的严格控制要求。
2)随着掌子面不断推进,上、下层预支护结构挠度最大位置逐渐向前推进,最终稳定在隧道中心(5.4 m)处。
3)预支护体系挠度变化的速率在隧道开挖中期(掌子面位于3~7 m)较显著。开挖前期与后期改变较小,经分析认为端部约束承担了此阶段大部分荷载增量。
4 参数分析
在双层预支护理论分析模型的基础上,进一步研究中间土体弹簧刚度、水平旋喷桩直径和管棚直径等参数对预支护结构挠度变形的影响。取隧道开挖完成工况,计算不同参数下预支护体系的挠度。
4.1 中间土体弹簧刚度
弹簧刚度依次取2.00×104,5.00×104,1.00×105,5.00×105和3.00×106kN/m 共5 个值,其他参数不变,所得预支护体系挠度随弹簧刚度变化如图8所示。由图8可知:
1)预支护体系通过中间土体弹簧达到协同变形的效果,表现为随着弹簧刚度增加,上层挠度逐渐减少,下层挠度逐渐增加;随着弹簧刚度逐渐增加,上层结构挠度最大值由-7.4 mm逐渐减小为-4.2 mm;下层结构挠度最大值由-3.8 mm 逐渐增加为-4.2 mm。
2)中间土体弹簧刚度存在合理取值范围,为5.00×105~3.00×106kN/m;当地基弹簧刚度由2.00×104kN/m 变化到3.00×106kN/m 时,上层结构挠度的减小幅度逐渐趋近于0。
4.2 水平旋喷桩直径
水平旋喷桩直径依次取300,600,900 和1 200 mm,其余参数不变,所得预支护体系挠度随旋喷桩直径变化如图9所示。由图9可知:
1)水平旋喷桩对双层预支护体系的挠曲变形影响显著。当水平旋喷桩直径由300 mm逐渐增大为1 200 mm时,上层结构的挠度最大值由-8.2 mm逐渐降低为-1.7 mm,下层结构的挠度最大值由-8.1 mm 逐渐降低为-1.5 mm,分别减小79.3%和81.5%。
2)水平旋喷桩直径存在合理取值范围。当旋喷桩直径由300 mm 增加到600 mm 时,上、下层预支护结构挠度分别降低48%和49%;当旋喷桩直径由900 mm增加为1 200 mm时,上、下层预支护挠度仅分别降低10%和11%。

图8 预支护体系挠度随弹簧刚度变化图Fig.8 Deflection of pre-support system varies with spring stiffness
4.3 管棚直径
管棚直径依次取108,133,159 和219 mm,其他参数不变,预支护体系挠度随管棚直径变化如图10所示。由图10可知:
1)随着管棚直径增加,预支护体系挠度逐渐减小;上层预支护结构挠度最大值由-4.4 mm逐渐减小为-4.2 mm,下层预支护结构挠度最大值由-4.3 mm逐渐减小为-4.0 mm。
2)管棚直径的增加对预支护体系挠度变形影响有限;当管棚直径由108 mm变化到219 mm时,上、下层预支护体系挠度减小量均约为0.2 mm,挠度未呈现大幅度变化。

图9 预支护体系挠度随旋喷桩直径变化情况Fig.9 Deflection of pre-support system varies with diameter of jet grouting pile

图10 预支护体系挠度随管棚直径变化情况Fig.10 Deflection of pre-support system varies with diameter of pipe shed
5 结论
1)将管棚和水平旋喷桩等预支护结构等效为梁单元,土体视作弹簧单元,支撑预支护结构两端的连续墙采用弹性支座模拟,采用不同的梁单元刚度模拟施工阶段抗弯刚度的变化,建立隧道双层预支护体系的力学分析模型,得到耦合挠曲微分方程组理论解,以确定预支护体系的变形状况。
2)在下层预支护的最大挠度方面,数值模拟结果与实测结果相对误差约5.1%,与理论分析结果相对误差约7.5%,理论结果与实测结果相对误差为2.5%,均在可接受范围内,认为建立的分析模型具有一定的可靠性。
3)中间土体弹簧通过变形,达到协调上、下层预支护体系挠曲变形的效果,弹簧刚度对体系的协同作用效果影响较大,旋喷桩直径对预支护体系挠曲变形有较大的影响,管棚直径的影响较小。综合考虑管廊保护与隧道安全施工,应重视对水平旋喷桩直径、中间土体加固强度等参数的控制。
