改进的鲸鱼优化算法及其在烧结配料中的应用
2020-02-25伍铁斌朱红求龙文李勇刚刘云连
伍铁斌,朱红求,龙文,李勇刚,刘云连
(1.湖南人文科技学院能源与机电工程学院,湖南娄底,417000;2.中南大学自动化学院,湖南长沙,410083;3.贵州财经大学贵州省经济系统仿真重点实验室,贵州贵阳,550025)
智能优化算法不需要目标函数具有连续的偏导数,具有稳定性强、能求解多极值问题、全局寻优能力较强等优点,在工业生产过程等得到了广泛应用[1-5],典型智能算法主要有PSO[6],ABC[7],CS[8],BA[9],GWO[10],GA[11]和 WOA[12]等。MIRJALILI 等[12]提出的鲸鱼优化算法(whale optimization algorithm,WOA)是通过模拟鲸鱼群体捕食猎物的过程提出的,具有原理简单、易于实现等优点,求解精度比PSO 的高。鲸鱼算法已经在电力无功功率的优化[13]和配电网的电容器选址[14]等工程领域得到应用,但WOA与其他智能算法一样存在易早熟的缺点。刘浩然等[15]提出了一种基于交叉变异算子和动态参数调整策略的WOA 算法。褚鼎立等[16]将模拟退火思想引入WOA 算法,并同时采用自适应权重的方法,兼顾了全局寻优能力和局部寻优能力。郑威迪等[17]用莱维飞行方法代替了原始WOA 的参数随机选择方法,加快了WOA算法的收敛速度。许瑜飞等[18]采用对立算子产生初始种群,使用精英反向学习策略提高了全局搜索能力,并结合差分进化进行变异修正,提高了算法的局部寻优能力,利用实际工程中的渣油加氢参数优化问题验证了算法的有效性。针对鲸鱼算法存在的问题,本文设计一种改进的鲸鱼算法(improved whale optimization algorithm,IWOA),基于指数函数的收敛因子平衡算法探索与开发能力,采用旋转因子提高局部寻优能力,并引入自适应变异操作以减少算法陷入局部最优的概率;通过标准测试函数验证改进的鲸鱼算法的有效性,并将其应用于烧结配料过程。
1 鲸鱼算法
基于鲸鱼独特的泡泡网觅食行为,MIRJALILI等[12]于2016年提出了鲸鱼优化算法(WOA)。在该算法中,假设鲸鱼种群规模为N,搜索空间为d维,第i只鲸鱼在d维空间中的位置可表示为Xi=(x1i,x2i,…,xdi),其中,i=1,2,…,N。猎物的位置对应于问题的解。
在WOA算法中,假设当前群体中的最优位置为猎物,群体中其他鲸鱼个体都向猎物靠近以更新自己的位置。利用下式更新位置:

式中:t为当前迭代次数;Xp=(x1p,x2p,…,xdp),为猎物位置,

式中:r1和r2为[0,1]之间的随机数;a为线性递减的收敛因子;k为当前迭代次数;kmax为最大迭代次数。
在WOA算法中,模拟鲸鱼螺旋式运动以捕获猎物的特点,设计了螺旋更新位置的方法,其数学模型为

式中:D′=|Xp(t)-X(t)|,为第i只鲸鱼和猎物间的距离;b为限定螺旋形状的常数;随机数l∈[-1,1]。鲸鱼不仅在猎物收缩圈周围游来游去,而且沿着螺旋形路径进行游弋。
除了泡泡网捕食行为外,鲸鱼也可以自由寻找食物,即根据彼此位置进行随机搜索,如下式所示:

式中:Xrand为从当前群体中随机选取的鲸鱼个体位置向量。
2 改进鲸鱼优化算法
2.1 基于指数函数的收敛因子
群体算法的全局探索能力与局部开发能力一样重要,必须平衡好全局探索能力与局部开发能力,收敛因子a越大,算法的探索能力越强,但不利于算法收敛;反之,则开发能力越强,同时也更容易早熟。在基本的WOA 算法中,收敛因子a随迭代次数从2 线性减小到0,特别是在求解多峰函数时,容易陷入局部最优。为此,提出一种基于指数函数的随着进化迭代次数呈非线性变化的收敛因子,在前期强调全局寻优能力的同时,在后期兼顾局部寻优,a的更新公式为

式中:λ为非线性调节系数(1<λ≤3);e 为自然常数;t为当前迭代次数;tmax为最大迭代次数。
2.2 基于旋转操作的精英学习方法
原始的鲸鱼算法具备一定的局部寻优能力,但在局部精细搜索上存在不足。为提高算法的局部寻优能力,引入一种基于旋转操作[9]的精英学习方法。本文选取精英比例δ较大的个体(15%<δ<40%)进行局部细搜索,如下式所示:

式中:R为[-1,1]之间服从均匀分布的随机向量(1×d维);R∙X(t)表示随机向量R与X(t)的点乘;β为旋转算子,为正数,

βmax为β的最大值(0.1≤βmax≤1);ω为收缩系数(1<ω≤2);ε为很小的数(10-10<ε<10-3)。在算法进化过程中,每进化1 代,则β除以调节系数ω,直到β小于ε时,重新给β赋值为βmax。
该旋转操作在以某一个个体为中心、β为半径的超球面内进行随机细搜索。β是动态变化的,因此,算法能在δ较大的个体周围进行多层次、小范围搜索,能有效提高寻找到次优解附近最优解的概率。
2.3 自适应变异操作
与其他群体算法一样,鲸鱼算法在进化后期容易陷入局部最优,且缺乏跳出局部最优的操作。因此,本文设计一种自适应变异操作算子,变异概率pm随着种群多样性的变差而增大,使得算法在进化后期能有效跳出局部最优。变异概率为
(1)地表出露的斑岩为以岩脉、岩株形式产出并侵入香夼组地层以及南部的南庄组地层,并具有大致顺层的特征。另外,隐爆角砾岩多位于浅成—超浅成中酸性斑岩体顶部[13],Wolfe[21]认为形成隐爆角砾岩的浅成—超浅成斑岩体往往是与深部大隐伏岩体相连的沿着软弱带向上侵入的小岩株,推测深部存在较大的隐伏岩体,岩脉、岩株向下汇聚为花岗闪长斑岩体。

式中:p0为变异概率的初始值(0.05<p0≤0.15);η为增幅系数;ζ为陷入局部最优解的诊断系数,若可能陷入局部最优,则ζ=1;若没有陷入局部最优,则ζ=0.5。

将所有解对应的适应度f按从大到小排序,fmin为最小适应度(fmin对应的解作为当前最优解);然后,选取适应度较小的61.8%(黄金比例)部分,假设该部分适应度的平均值为fGR_mean,ρ1/100和ρ2/100为群体多样性诊断参数(满足0<ρ1/100<ρ2/100<10/100,ρ1和ρ2为(0,10)之间的常数)。当fmin=0 时,η取0.3。显然,|越小,则解的多样性越差,因此,需要取更大的变异概率,以便有效跳出局部最优。

式中:k为当前迭代的代数(当k<3时,ζ取1)。当连续3代的最优解没有改善(即连续3代的最优解相同)时,极有可能陷入了局部最优,因此,需要取较大的变异概率以便跳出局部最优,此时,ζ取值为1。
2.4 改进的鲸鱼算法步骤
本文提出的改进的鲸鱼算法(简称IWOA)流程图如图1所示。
3 数值实验及比较
3.1 测试函数及性能指标
为了验证本文提出的IWOA 算法的性能,选取10 个具有代表性的标准函数进行测试。10 个标准测试函数如表1所示,其中,F1~F4为维数可变的单峰函数,F5~F8为维数可变的多峰函数,F9和F10为固定维数的多峰函数,fmin为理论最优值。
3.2 实验结果
将本文提出的IWOA 算法与基本WOA 算法[12]、基本PSO 算法[6]进行比较,为公平比较,取这3 种算法的种群规模均为30,最大的迭代次数tmax均为500次。在IWOA算法中,收敛因子中的非线性调节系数λ=1.5,旋转系数βmax=0.5,收缩系数ω=1.2,精英比例δ=25%,变异概率中p0=0.1,增幅参数η初始值为0.15。这3 种算法在上述参数下独立运行20 次,记录最优值和平均值。这3 种算法对各测试函数的寻优收敛曲线(随机选取某一次)如图2所示。从图2可知:IWOA 收敛速度明显比其他2种算法的高,寻优精度也较高。表2所示为PSO[6]、灰狼优化算法(GWO)[20]、WOA[12]和本文的IWOA 这4 种算法独立寻优20 次的统计结果,其中,GWO的平均值为文献[20]中的仿真结果(文献[20]中函数F1~F8的变量取30维)。

图1 改进的鲸鱼算法流程图Fig.1 Flow chart of improved whale algorithm

表1 测试函数Table 1 Test functions

表2 IWOA,WOA,PSO和GWO算法对10个测试函数的寻优结果比较Table 2 Comparison of IWOA,WOA,PSO and GWO algorithms for 10 test functions
4 IWOA 算法在钢铁烧结配料中的应用
烧结过程是我国钢铁冶炼的关键工序,对保障高炉炼铁极其重要;贫铁矿或铁精矿粉必须经过烧结成块,才能进入高炉冶炼。炼铁烧结过程主要由一次配料、二次配料和烧结热过程这3个级联工序组成。一次配料为烧结前的关键工序,是将多种化学组分不一样的铁矿石粉混合在一起形成铁矿石中和粉,决定了烧结块的化学成分[21]。通过配料过程既降低成本,同时将有害的化学成分控制在一个合理的区间内。

图2 基法IWOA、基本WOA和基本PSO对10个标准测试函数的寻优曲线Fig.2 Optimization curves of 10 standard test functions based on IWOA,basic WOA and PSO
4.1 烧结配料数学模型
由于不同的铁矿石化学成分和价格都不一样,不同的配比导致价格差异非常大。某钢铁企业的7种铁矿原料中TFe,P,S,Al2O3,SiO2和MgO 的质量分数(分别用p1,p2,p3,p4,p5和p6表示)和价格如表3所示。

表3 铁矿粉的化学成分(质量分数)与价格Table 3 Chemical composition(mass fraction)and price of iron ore powder
4.1.1 目标函数
配料的目的是要提高烧结矿的质量和降低成本,因此,建立以经济成本最小为原则的目标函数。

式中:k为参与配料的矿的种类;ck为每种矿的单价(元/t);xk为每种矿的用量(xk≥0)。
4.1.2 混合矿中TFe约束条件

4.1.3 混合矿中磷(P)和硫(S)的约束条件

4.1.4 混合矿中Al2O3,SiO2和MgO的约束条件

4.2 模型求解
采用本文提出的IWOA 求解该配料问题,并与标准PSO 算法、基本WOA 算法进行对比(都采用Deb 准则处理约束),结果如表4和表5所示。从表4和表5可知:假设某企业每年配料为100 万t,在满足各约束的条件下,采用IWOA 算法与采用标准粒子群算法、GWO 算法和WOA 算法相比,每年分别可以节约632.76 万元、227.77 万元和400.77万元,取得了显著的经济效益。本算法有效地解决了钢铁冶炼过程中的烧结配料优化问题,由于其他冶金领域的配料问题与钢铁烧结过程的配料问题具有相似性,因此,本算法也适用于解决其他冶金领域的配料问题。
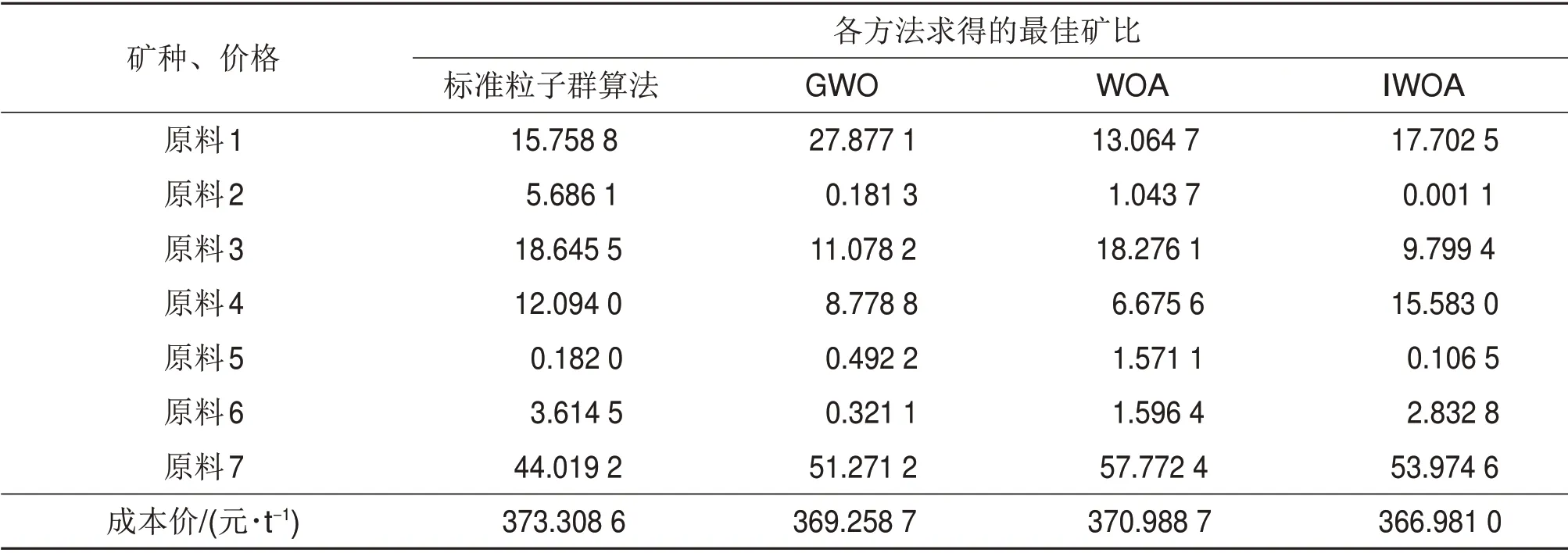
表4 不同算法优化计算的最佳矿比及成本价的对比Table 4 Comparison of the best ore ratio and product cost resulting from different algorithms %

表5 采用不同算法优化得到的混合料中各元素质量分数Table 5 Mass fraction of some elements of mixed material obtained by different algorithms %
5 结论
1) 鲸鱼优化算法(WOA)是一种模拟鲸鱼捕食行为的新型智能算法,针对基本鲸鱼优化算法的不足,提出一种改进的鲸鱼优化算法(IWOA)。
2)利用10 个标准测试函数验证了IWOA 具有收敛速度快、全局寻优能力强的优点。将IWOA应用于钢铁烧结配料过程,仿真结果表明IWOA能有效降低配料过程的成本。
