中速永磁风电机组控制系统滤波器研究及应用

汪亚洲，蔡 新，李其龙，许波峰

（1.河海大学 力学与材料学院，江苏 南京 210098； 2.中建材南京新能源研究院，江苏 南京 211100）

0 前言

按照传动方式的不同，风力发电机组分为直接驱动型和增速驱动型，其典型代表分别是直驱永磁机组和高速双馈机组。 近年来，中速永磁技术已成为继直驱永磁和高速双馈后的第三主流技术路线，受到越来越多整机厂商的关注[1]，[2]。

典型中速永磁机组具有三叶片、 变桨控制、中速齿轮箱、中速永磁同步发电机和全功率变流等特征，是在综合考虑直驱机型和双馈机型优缺点的基础上，优化设计的新一代风电机组。 典型中速永磁机组既保留了直驱机型和双馈机型的优点，又对两种机型的不足进行了结构优化，增强了机组可靠性，降低了制造成本和维护成本。控制系统是风机运行发电的核心，其响应速度和可靠性决定了整机控制策略的可实现性和运行的稳定及可靠性。 滤波器作为控制系统的重要组成部分，将直接影响控制系统性能。

文献[3]结合风电机组共振坎贝尔图，分析了带阻滤波器对风电机组塔架振动控制的影响，通过在转矩控制器中串联带阻滤波器的方法，研究滤波器对塔架振动的影响。文献[4]研究了基于阻尼滤波的大型风电机组柔性振动控制技术，针对变速机组的振动、冲击载荷问题，提出阻尼滤波的设计方法，施加到转矩、变桨控制器中。 本文将从时频域角度分析滤波器的性能及影响参数，通过仿真来验证参数对滤波器性能的影响。

1 基本理论

数字滤波器具有实现简单、 参数调整方便和滤波效果好等优点，在大型风电机组控制系统中得到广泛应用。

1.1 滤波器在控制系统中的作用

风电机组控制系统主要通过转矩控制和变桨控制来实现转速控制，其原理如图 1 所示[5]，[6]。

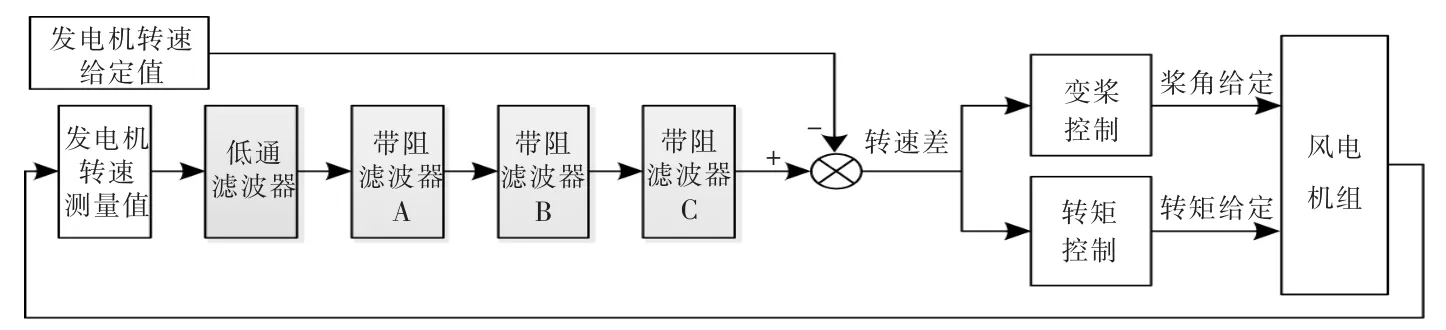
图1 风电机组控制原理图Fig.1 Wind turbine control schematic diagram

将发电机给定值与测量值之差作为控制器输入，相应的转矩给定和桨角给定作为控制器输出。然而，由于风电场湍流、风机振动和电磁干扰等因素影响，采集到的转速信号中含有大量其他频率成分的干扰信号，这些干扰信号不仅影响控制效果，甚至影响控制系统稳定性。 因此，在对信号进行控制输入前，须对测量到的转速信号进行滤波处理，可采用低通滤波器滤除信号中的高频噪声。除低通滤波器外，如果在机组的整个变速运行过程中，塔架模态或叶片振动模态与叶轮旋转频率及其倍频等发生交越，可能产生机组共振。 在系统控制上，可采用带阻滤波器将其滤除。

1.2 滤波器数学模型

数字滤波器的输入 x（n）和输出 y（n）的关系可用如下常系数差分方程及其Z 变换描述[7]：

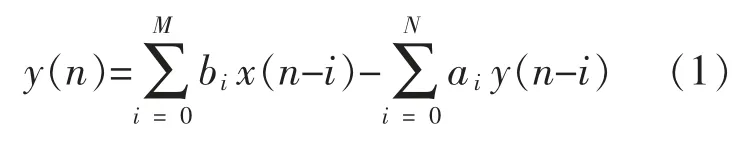
式中：x（n），y（n）分别为输入和输出信号时间序列；ai，bi为滤波器系数。

对式（1）两边进行Z 变换，得到数字滤波器的离散传递函数：

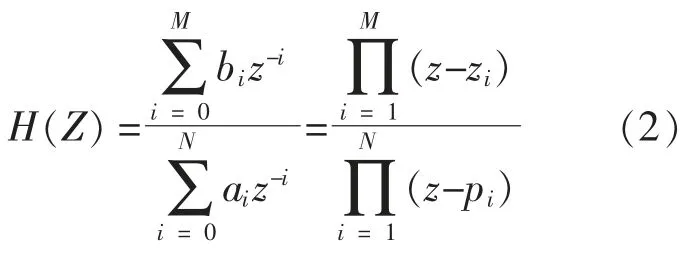
式中：zi，pi分别为传递函数的零点和极点。

1.3 基本形式及频域特性

本文主要研究二阶低通滤波器和带阻滤波器。 二阶低通滤波器连续传递函数如下[8]：

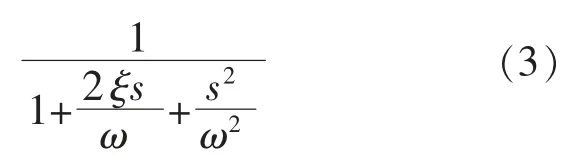
根据经典自动控制理论，二阶振荡环节在穿越频率处的幅值裕度h 为

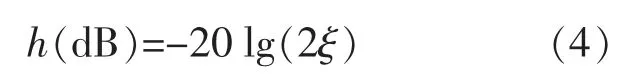
在MATLAB 中对该传递函数进行编程，并绘制伯德图（Bode）。设定穿越频率ωx=10 rad/s，当阻尼比 ξ 分别为 0.1，0.3，0.7，1.0 时，穿越频率处的幅值分别为 13.97，4.44，－2.92，－6.02，其频率特性曲线如图2 所示。 从图2 中可以看出，穿越频率处的幅值随阻尼比增大而减小，穿越频率ωx影响频率特性的拐点，而阻尼比ξ 影响曲线变化趋势。因此，低通滤波器滤波效果取决于这两个参数。

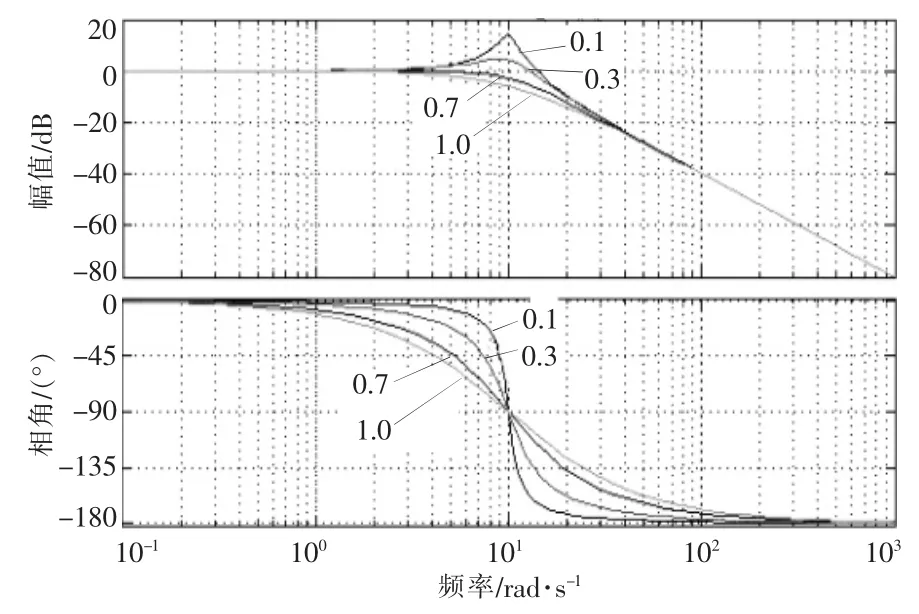
图2 低通滤波器的伯德图Fig.2 Bode diagram of low pass filter

通用的二阶滤波器连续传递函数如下：

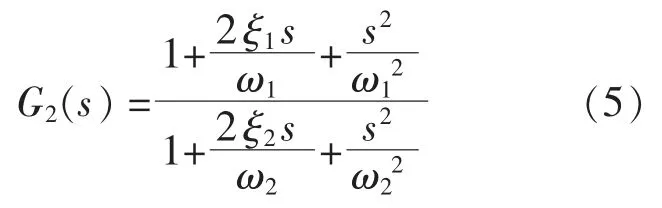
同理，根据式（3）、式（4）可得穿越频率处的幅值裕度h：

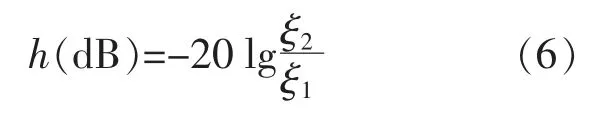
当 ω1=ω2=ω，且 ξ1＜ξ2时，带阻滤波器（也称陷波器） 可以滤除特定频率 ω，ξ2与 ξ1比值决定带阻滤波器的深度。 通常调到对特定频率有明显滤波效果而对其他频率没有过多影响为止。

设定 ω1=ω2=4 rad/s，分别选取 3 组阻尼比（ξ1=0.01，ξ2=0.05；ξ1=0.01，ξ2=0.20；ξ1=0.01，ξ2=1.00）时，其频率特性如图3 所示。 从图3 可以看出，可以通过选取阻尼比ξ2与ξ1来调节期望频率处的幅值陷波深度。

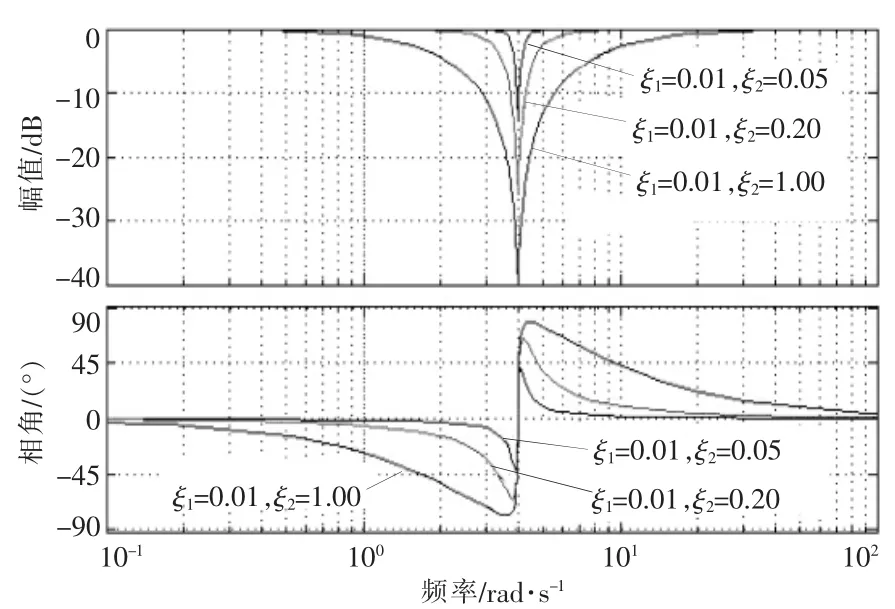
图3 带阻滤波器的伯德图Fig.3 Bode diagram of notch filter

2 滤波器设计及仿真验证

传统的数字滤波器设计计算繁琐，尤其是设计高阶滤波器的工作量大，利用MATLAB 可以快速有效地实现数字滤波器的设计与仿真。 本文基于MATLAB 平台m 语言对IIR 数字滤波器进行设计以及仿真验证。

2.1 设计步骤

以低通滤波器为例，根据数学模型式（1），以ai和bi为时域参数。 由于时域参数没有特定物理含义，不便于参数调节，因此根据滤波器的频域特性，使频域参数穿越频率ω 和阻尼比ξ，直接影响滤波器效果。 这样只须找出频域参数ω，ξ 与时域参数ai，bi的对应关系，即可设计出相应滤波器。具体步骤如下。

步骤1 根据连续传递函数公式，已知参数ω 和ξ，得出传递函数的分子分母系数矩阵A=[1]和 B=[1/ω/ω，2 ξ/ω，1]；

步骤2 调用tf 函数，得到传递函数sys=tf（A，B），如 sys=tf（[12]，[138]）表示传递函数（s+2）/（s2+3 s+8）；

步骤3 调用c2d 函数，将连续系统离散化处理为离散系统，sysd=c2d（sys，Ts，method）。式中：Ts为采样周期，即 Ts=1/Fs；Fs为采样频率；method可选 zoh 零阶保持器法、foh 一阶保持器法和tustin 双线性变换法。 为防止出现频率混叠现象，选用双线性法，即 sysd=c2d（sys，Ts，′tustin′）；

步骤4 进行Z 变换的逆变换，转成时域表达式。 调用tfdata 函数提取分子、分母的系数，即[b，a]=tfdata（sysd，′v′）。 因此，时域参数 ai，bi可由频域参数ω，ξ 求出，从而得到二阶低通滤波器时域表达式。

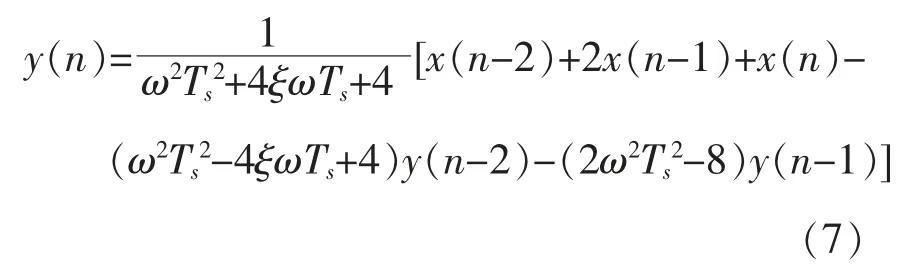
同理，可以得出二阶带阻滤波器时域表达式：

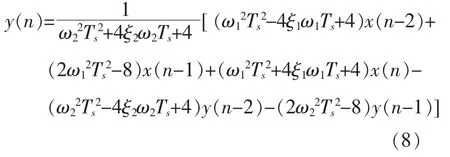
步骤 5 结合式（1），可得出时域参数 ai，bi。

步骤 6 调用 filter 函数，即 y=filter（b，a，x），其中 filter 为滤波器函数；b，a 为滤波器系数；x 为滤波前信号；y 为滤波后信号。

2.2 仿真验证

为验证滤波器设计方法的有效性，在MATLAB 平台上利用仿真信号进行验证。 设有一个输入信号 x（t），它由 50 Hz 信号和 150 Hz 信号组成，即：

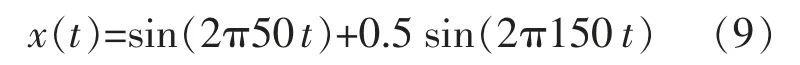
2.2.1 低通滤波器的仿真验证

设计一个低通滤波器，干扰信号为150 Hz，采样频率为 400 Hz。参数设置为 ω=2π100，ξ=0.7。仿真结果如图4 所示。由图4 可以看出，干扰信号150 Hz 被成功滤除，且对50 Hz 频率没有影响，故满足滤波要求。

2.2.2 带阻滤波器的仿真验证

设计一个50 Hz 的带阻滤波器，采样频率为400 Hz。 设定参数为 ω1=ω2=2π50；ξ1=0.01；ξ2=0.10。 仿真结果如图5 所示。 由图5 可以看出，干扰信号50 Hz 被成功滤除，故满足滤波要求。

图5 带阻滤波器滤波效果Fig.5 The effect of notch filter

通过以上仿真验证表明，本文提出的滤波器设计方法合理有效，可将此方法应用到中速永磁风电机组控制系统的控制策略设计中。

3 实例应用

为验证以上提出的滤波器设计方法在控制系统控制策略中的有效性，选取某厂家2.0 MW-131中速永磁机组为对象进行应用研究。 首先，通过Bladed 软件建立风机模型；然后，利用软件自带的模型线性化功能模块，提取风机模型线性化数据；最后，导入到MATLAB 中被控制器调用。风机总体技术参数见表1。

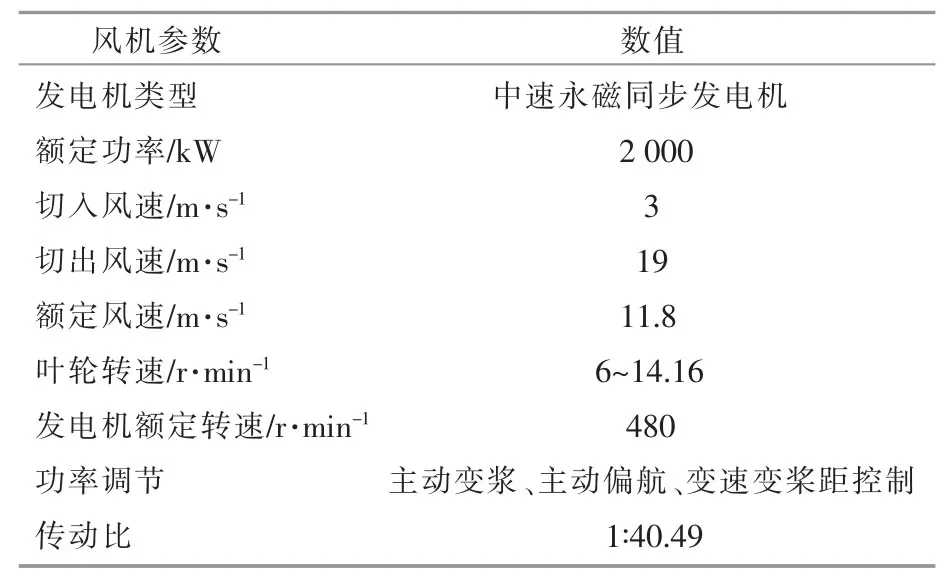
表1 风电机组总体技术参数Table 1 Overall technical parameters of wind turbine

3.1 滤波器在转矩控制器设计中的应用

转矩控制器为PI 控制器叠加1 个低通滤波器和3 个带阻滤波器，带阻滤波器包含3 P，6 P 和叶片二阶面内振动模态。 通过调节穿越频率ω 和阻尼比ξ，可以将转矩控制器调整到合理范围内。

图6、 图7 为在风速 8 m/s 下滤波器使用前后转矩控制器的伯德图和发电机转速对于风速阶跃变化的时域响应图。 从图6、图7 可知，使用滤波器后转矩控制器在频率为8.7 rad/s 时的幅值裕度为 17 dB； 在频率为 0.48 rad/s 时的相角裕度为63.2 °；发电机转速对于风速阶跃变化的时域响应波动明显降低。该结果符合控制器稳定性要求，表明滤波器满足设计要求。

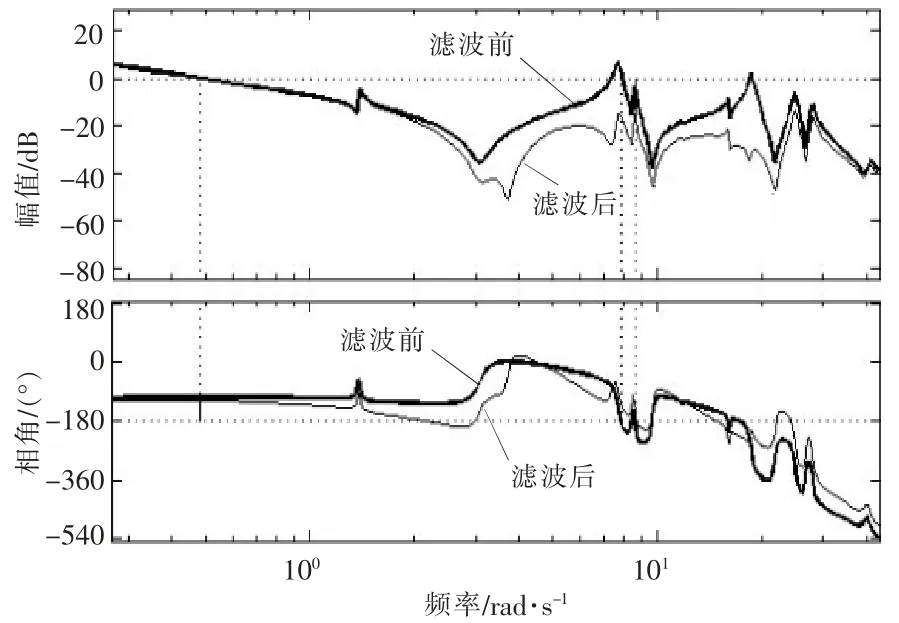
图6 8 m/s 风速下，滤波器使用前后转矩控制器伯德图对比Fig.6 Comparison of the Bode diagram of the torque controller before and after filtering at 8 m/s wind speed

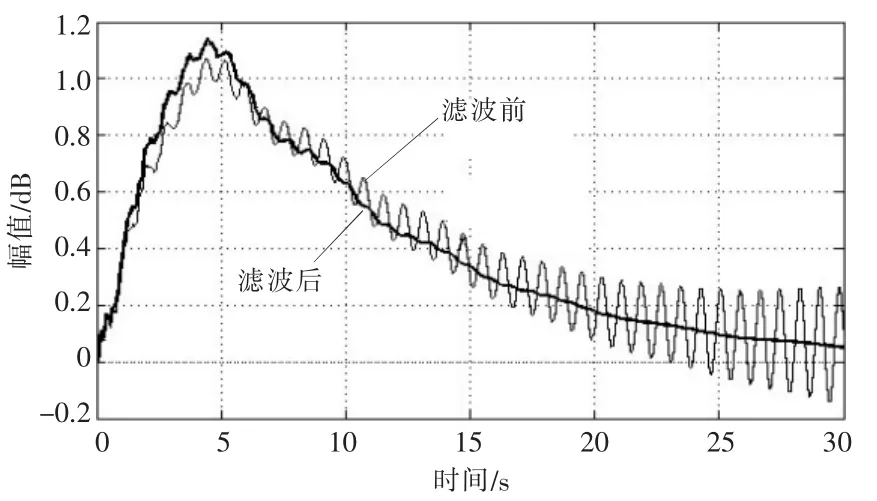
图7 8 m/s 风速下发电机转速滤波前后时域响应Fig.7 Time-domain response of generator speed before and after filtering at 8 m/s wind speed

3.2 滤波器在变桨控制器设计中的应用

变桨控制器为PI 控制器叠加1 个低通滤波器和2 个带阻滤波器，带阻滤波器包含6 P 和叶片二阶面内振动模态。 图8、图9 分别是在16 m/s风速下使用滤波器前后的变桨控制器伯德图和叶片1 桨角对于风速阶跃变化的时域响应图。

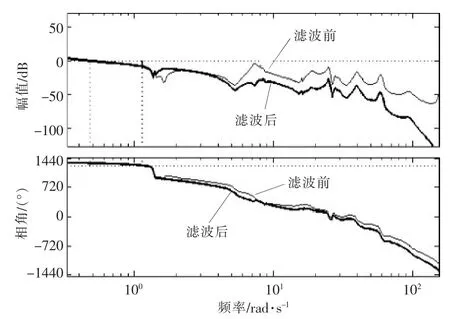
图8 16 m/s 风速下滤波器使用前后变桨控制器伯德图对比Fig.8 Comparison of the Bode diagram of the pitch controller before and after filtering at 16 m/s wind speed

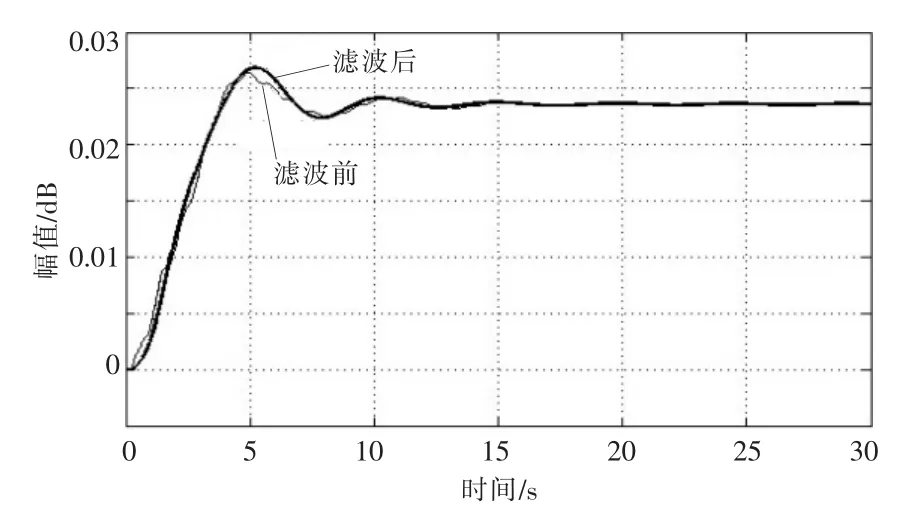
图9 16 m/s 风速下滤波器使用前后叶片1 桨角时域响应Fig.9 Time-domain response of blade 1 pitch angle before and after filtering at 16 m/s wind speed

由图8，9 可以看出，使用滤波器后变桨控制器在频率为1.14 rad/s 时的幅值裕度为8.73 dB；在频率为0.481 rad/s 时相角裕度为59°；符合控制器稳定性要求。叶片1 桨角对于风速阶跃变化的时域响应波动更加平滑，表明滤波器设计满足要求。

4 结束语

本文从滤波器的基本原理入手，介绍了在风电机组控制系统中广泛应用的低通滤波器和带阻滤波器的时频域特性；基于MATLAB 平台模拟仿真，验证分析了频域参数对滤波器性能的影响；实现了滤波器时域与频域的相互转换。 将研究结果应用于某2.0 MW 中速永磁机组控制系统设计中，控制器达到了理想效果，为滤波器在中速永磁机组的工程应用提供了一种设计方法与思路。