基于SA算法的主动配电网网损优化模型研究

曾 鸣，王雨晴，刘英新，闫 彤，武 赓，孙辰军

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.电力规划设计总院，北京 100120；3.国网河北省电力公司，河北 石家庄 050000）

0 引言

随着分布式电源的发展，传统配电网面临电压越限、双向潮流等问题[1]，[2]，配电网由被动控制过渡到主动控制[3]。主动配电网可以实现分布式电源广泛接入并高度渗透，是综合控制分布式资源（例如分布式电源、柔性负载、储能等）、通过灵活的网络调节技术实现潮流有效管理的重要技术手段[4]～[6]。系统网损是主动配电网运行经济性的重要衡量指标[7]，[8]。优化主动配电网系统网损，提高其运行经济性，对于未来主动配电网的建设发展具有重要意义。

目前，国内外学者针对网损优化问题开展了深入的研究。文献[9]建立了系统有功网损优化模型，并通过在线实时优化潮流计算进行求解。文献[10]针对异步联网的交直流混联系统，建立网损优化模型并推导最优解条件。文献[11]考虑风电场有功出力和功率因数对配电网网损的影响，对配电网进行计及网损最小的多目标优化。上述文献均以系统网损最小为优化目标，结合系统潮流计算建立并求解优化模型以优化网损。但是分布式电源功率输出的波动性使得主动配电网的优化策略十分复杂，基于传统最优潮流的优化模型及其计算方法对主动配电网已不适用[12]～[14]。文献[15]针对含分布式电源的配电网，建立有功网损优化模型，结合粒子群算法和配网潮流计算进行求解。文献[16]提出了基于机会约束规划的风电并网系统的有功潮流优化模型，将粒子群算法和随机模拟算法相结合进行求解。文献[17]建立了考虑风速随机性的概率最优潮流模型，应用基于随机模拟技术的粒子群优化算法求解模型。

上述研究均在模型中考虑分布式电源出力的波动性，但是均需要循环多次的潮流计算，计算较复杂，难以快速求得最优解。本文提出了一种基于SA 算法的主动配电网网损优化模型及其求解流程，通过SA 算法建立变量间的微分关系，确定网损对可再生分布式出力的敏感程度，从而避免多次的OPF 模型计算，大大降低求解难度、缩短求解时间。在华北地区某34 节点配电网系统中对所提模型进行仿真计算，通过对比所提模型和算法与传统OPF 的计算误差及时间，验证了其有效性。

1 考虑分布式电源的主动配电网网损优化模型

1.1 传统最优潮流模型

配网系统网损优化主要是基于传统OPF 模型求解，该过程是一个大规模混合非凸非线性优化问题。传统OPF 模型是以系统有功网损最小为目标，在考虑系统有功、无功平衡以及线路潮流、节点电压约束的条件下，对某一时间断面的系统机组出力、 线路潮流和节点电压以及非自愿负荷中断量等系统稳态变量进行决策和优化，从而达到优化系统网损以及系统运行策略的目的。本文主要针对接入分布式风电或者光伏的主动配电网系统的网损优化问题，假设该主动配电网系统的主网变压器不包含变压器抽头和其他的无功补偿装置，对传统OPF 模型进行了简化，其状态方程为

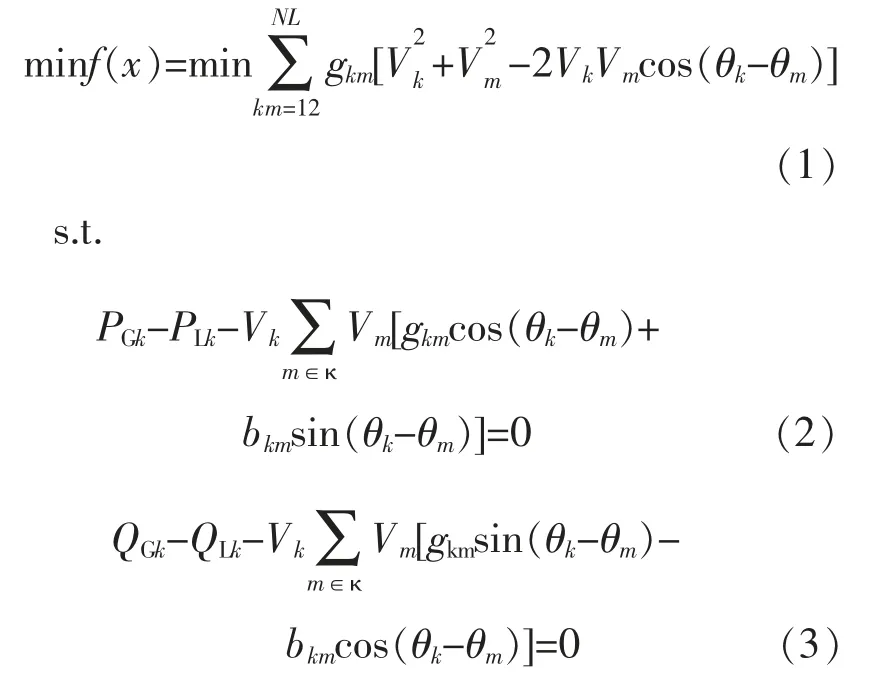
式中：k，m 为系统节点序数；km 为连接节点 k，m线路序数，例如，km=12 表示连接节点1 和节点2之间的序数；NL 为线路序数集合；Vk，Vm为节点k，m 处的电压值；θk，θm为节点 k，m 处的电压相角；bkm，gkm分别为导纳矩阵的实部、虚部，表示线路 km 的电导、电纳值；PGk，QGk分别为节点 k 处接入的分布式电源或变压器的有功、无功功率；PLk，QLk分别为节点 k 处负荷的有功、 无功功率；κ 为与节点k 相连的其余节点集合。

由于本文研究的重点是可再生分布式电源出力（包括有功和无功）波动对于系统稳态变量及网损的影响，所以须对传统OPF 模型进行进一步简化，暂不考虑线路容量以及节点电压的上下限约束[18]。

1.2 SA算法

由于可再生分布式电源的接入，其出力的波动特性使得系统稳态变量的最优控制策略需要进行调整，从而尽量减小系统网损。因为传统OPF模型的非凸、非线性，其求解较为复杂，求解时间较长。本文将采用基于拉格朗日的SA 算法对接入可再生分布式电源的主动配电网最优潮流问题进行求解，避免进行多次OPF 计算，降低优化的求解难度和优化时间。

SA 算法主要用于在已知优化问题原始解的条件下，当模型输入参数出现扰动，须要对模型原始解重新进行调整，根据原始解和输入参数的扰动量对当前优化问题进行处理[19]，[20]。其应用的一般数学问题表述式为

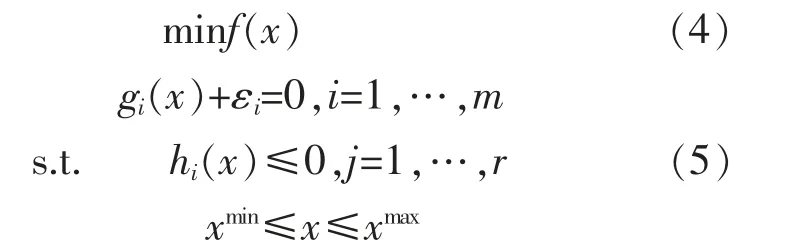
式中：f（x）为优化问题的目标函数，本文中为系统网损；x 为优化决策变量，本文中为系统线路潮流和节点电压；εi为优化模型输入变量的扰动值，本文中为分布式可再生能源机组出力的扰动值；hi（x）为优化问题的不等式约束；xmax，xmin为决策变量x 的上、下限约束。

首先将SA 算法通过拉格朗日算法对原始问题进行求解，得到输入变量扰动之前的原始局部最优解（x*，μ*，λ*），其中，x*为决策变量原始解，μ*和λ*分别为不等式约束和等式约束拉格朗日乘子的原始解。本文中（x*，μ*，λ*）即为不考虑可再生分布式电源出力波动系统某一时间断面OPF 模型的局部最优解。

当输入变量出现扰动值εi后，优化问题的拉格朗日形式为

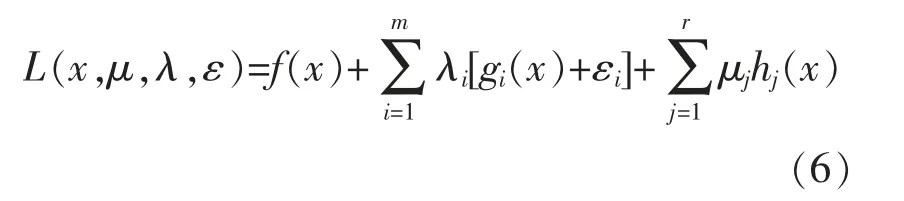
式中：λ 为等式约束的拉格朗日乘子；μ 为不等式约束的拉格朗日乘子。

当 f（x），gi（x）和 hj（x）均二阶可微时，x 为局部最优解的必要条件是存在 λ 和 μ 使得（x，μ，λ）满足一下条件：

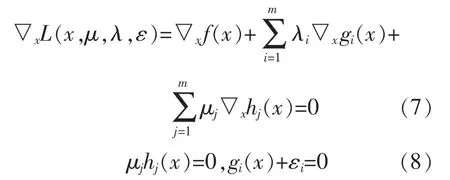
对式（7），（8）进行线性化后，可得到：

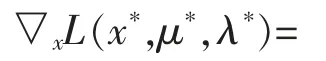
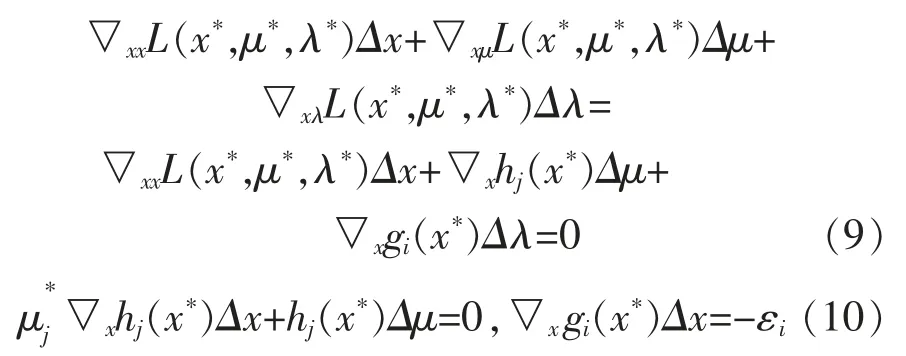
输入变量扰动后，原始问题的新局部最优解可表示为 （x*+Δx，μ*+Δμ，λ*+Δλ），其中（Δx，Δμ，Δλ）为式（9），（10）的解，其矩阵形式为

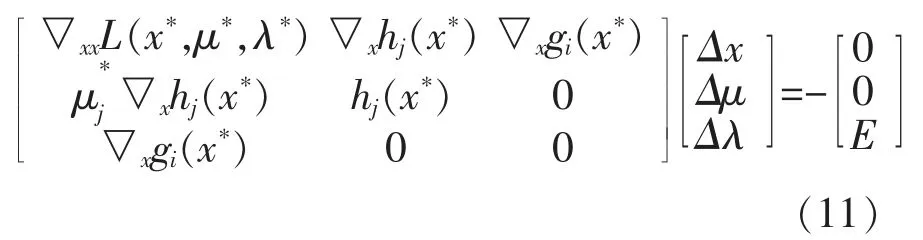
对式（11）中右侧参数矩阵进行求逆，可得：

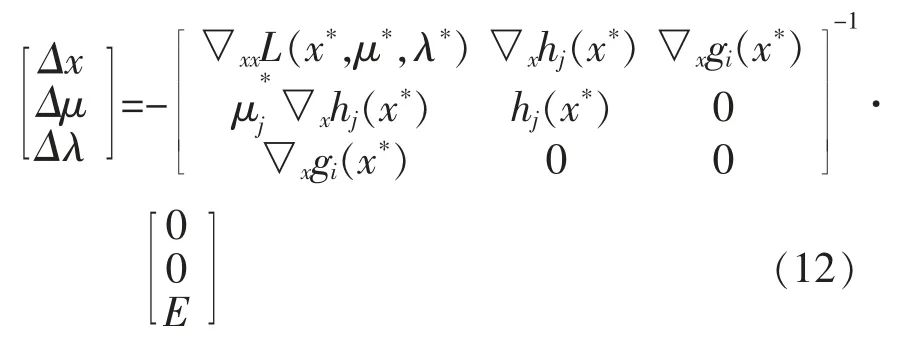
基于本文中简化的OPF 模型，不考虑模型中的等式约束，则式（12）可简化为

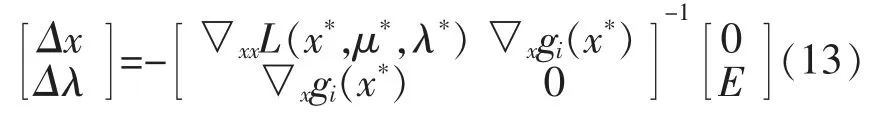
由式（13）可知，输入变量出现扰动后，式（1）的局部最优解为

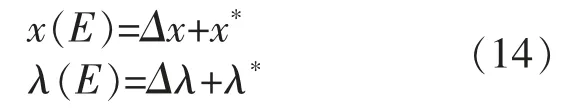
式中：x（E），λ（E）为输入变量扰动后优化问题的新局部最优解。

1.3 可再生分布式电源出力模型

本文以风电机组为例，对接入分布式风机主动配电网系统的OPF 进行计算。分布式风机出力波动主要来自于风速的不确定性，本文中假设风速随机变化特性近似服从Weibull 分布[21]。可基于Weibull 概率分布对风速进行随机抽样，得出风速波动序列V={vt}，进而基于风速-出力关系函数，得出分布式风机出力[22]。风速-出力关系函数为

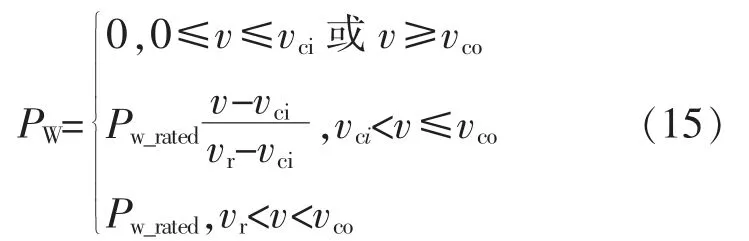
式中：vci为切入风速；vco为切出风速；vr为额定风速；Pw_rated为风机的额定功率。

2 考虑分布式电源的网损优化模型求解流程

根据考虑可再生分布式电源的主动配电网网损优化以及分布式风机出力模型，基于SA 算法的考虑可再生分布式电源OPF 求解流程如下。①确定所需测算主动配电网的相关参数，包括主动配电网拓扑结构，各个节点有功、无功功率、线路阻抗和线路长度等。②基于传统OPF 模型，得出不考虑分布式风机的各个时段的初始局部最优解（x*t，μ*t，λ*t）以及主动配电网的最小网损 f（x*t），t=1，2……8 760。③基于 Weibull 概率分布函数，通过随机抽样得出风速年时序序列V={vt}，t=1，2……8 760；进而根据式（15）得出分布式风机的年出力时序序列 PW（t），t=1，2……8 760。④将各时段的风机出力PW（t）作为模型输入变量的扰动值ε，基于 SA 算法和初始局部最优解（x*t，μ*t，λ*t），求解考虑分布式风机的新局部最优解（x*t，μ*t，λ*t）以及目标函数值 f（xt）。

同理，上述流程也可以用于单一时间断面系统网损求解，其中t 为某一特定时段。

3 仿真结果

3.1 系统参数

本文将在华北地区某34 节点配电网系统中对上述模型进行仿真验证，系统基本拓扑结构如图1 所示，主动配电网系统的相关参数如表1 所示。

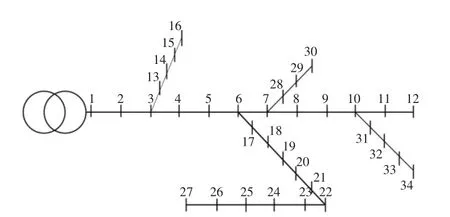
图1 华北地区某34 节点配电网系统Fig.1 Node diagram of a 34 node system in north China

表1 34 节点系统参数Table 1 34 nodes system parameters

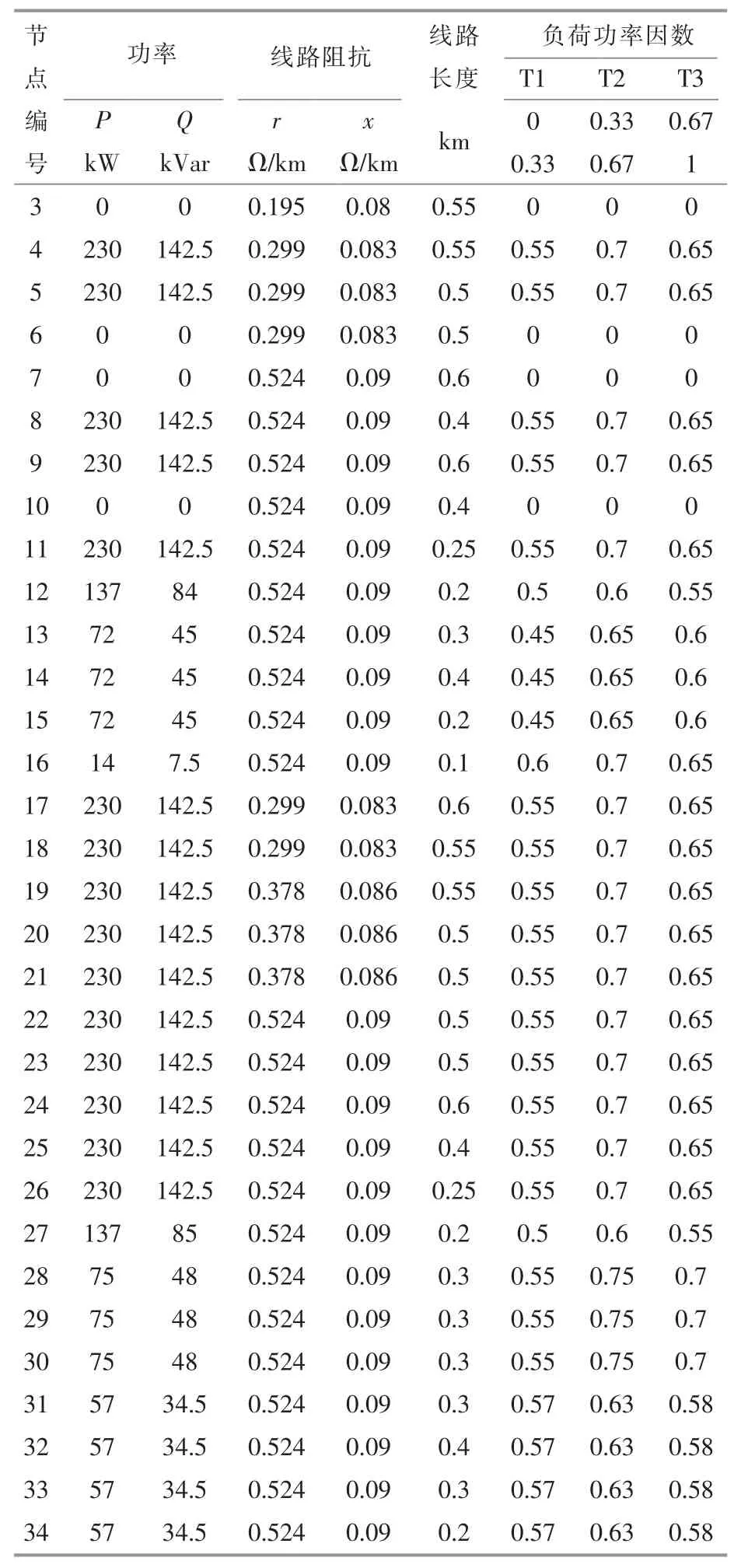
续表1

3.2 SA算法有效性

本部分通过设置3 种不同场景对SA 算法有效性进行验证。本文中通过SNOPT 非线性优化求解器对模型进行求解，不接入分布式风机时，系统原始网损为0.184 MW·h。

本部分假设系统中接入的分布式风机总容量为3 MW，且只考虑单一时间断面的系统网损。场景 1：基于该地区的平均风速，利用式（15）对3 MW 风机出力进行等效计算，平均风速为5.7 m/s，等效后接入风机在该时间段出力为500 kW。场景2：基于该地区风电场的平均容量系数，对3 MW风机出力进行等效计算，等效后接入风机在该时间段出力为1.2 MW。场景3：分布式风机按照3 MW 最大出力进行计算。基于上述场景，分布式风机在不同节点接入的系统网损如图2～4 所示。

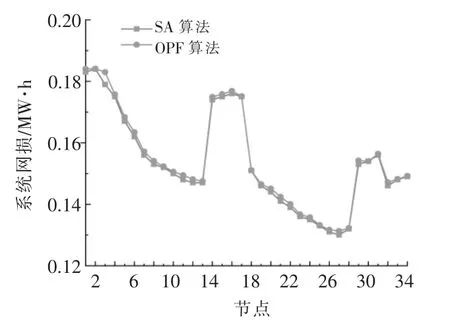
图2 场景1 下的系统网损Fig.2 System network loss under scenario 1

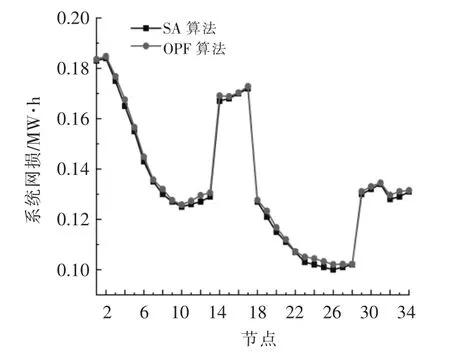
图3 场景2 下的系统网损Fig.3 System network loss under scenario 2

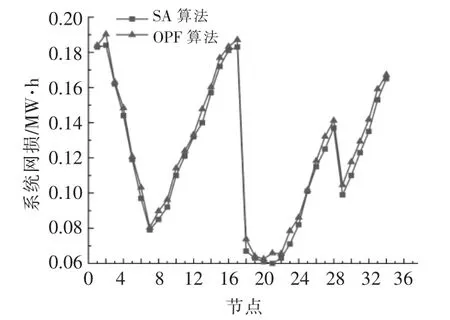
图4 场景3 下的系统网损Fig.4 System network loss under scenario 3

由图2～4 可知，与传统OPF 所求得的在各节点接入风机后系统网损误差相比，SA 算法所得的结果均较小，场景 1，2，3 下 SA 算法所求得结果各节点平均误差分别为0.000 7，0.001 4，0.004 1 MW·h，说明SA 算法具有较好的精确度，与OPF算法结果相差不大。同时可以发现，不同容量的风机接入系统网损也具有一定的差异，在不同节点接入风机对系统网损造成的影响也不同，场景1中分布式风机的最优接入位置为节点27，场景2中为节点26，场景3 中为节点20，较系统原始网损分别下降了28.9%，45.3%，67.2%，分布式风机的接入能够在一定程度上降低系统网损。

3.3 考虑风机出力不确定性的系统网损

由算例3.2 部分的结果可以看出，SA 算法与传统OPF 模型求解的结果误差很小，风机的最优接入位置也是一致的。为了进一步验证SA 算法的有效性和计算效率，本部分将考虑风机出力的不确定性，根据Weibull 分布和公式（15）产生分布式风机出力的年时序序列，计算该主动配电网年系统网损，得出该主动配电网系统中最优接入位置为节点25，在该节点接入分布式风机系统网损最小，具体如表2 所示。

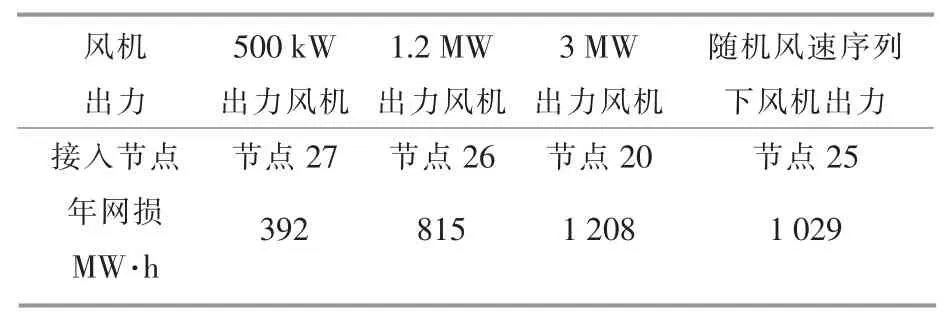
表2 主动配电网年系统网损Table 2 Annual system loss of active distribution network

由表2 可知，如果用当地平均风速、风电场平均容量因素或者最大出力来替代或者近似风机实际出力（Weibull 概率分布函数抽样得出），都会对系统网损的估计造成较大的误差，同时也会对分布式风机最优接入位置的选择造成一定的影响。这说明分布式风机出力不确定性是主动配电网网损以及分布式风机接入位置优化中必须考虑的因素。

当考虑分布式风机出力不确定性后，系统的网损优化问题求解更为复杂。在计算系统单一时间断面的网损时，SA 算法就较传统OPF 算法具有更快的求解速度，但因为求解断面较少，求解速度优势不明显。在计算主动配电网的年系统网损时，SA 算法的求解效率要大大高于传统OPF，在平台上通过matlab 中的tic-toc 函数可以得出传统 OPF 求解时长为 42 872 s，而 SA 算法则为3 507 s。传统OPF 算法得出的系统网损为1 057 MW·h，SA 算法的系统网损为 1 029 MW·h，二者计算得出的系统年网损误差为2.7%。可以看出，在优化结果相差不大的情况下，SA 算法的计算效率远远高于传统OPF，因此，SA 算法对于考虑可再生分布式电源的最优潮流和系统网损优化问题具有较好的适用性。

4 结论

本文提出了一种基于SA 算法的主动配电网优化模型及其求解流程，通过在34 节点配电网系统中进行仿真计算，得出以下结论：①针对主动配电网的网损优化问题，SA 算法较传统的OPF 算法具有更快的求解效率，且能够将计算误差控制在一定范围内；②主动配电网中分布式风机出力的不确定性能够对其最佳接入节点位置以及系统网损优化结果造成较大的影响，使用其他形式的风机等效出力都与实际的计算结果有一定的误差。