不同尺度DEM对面雨量估算模型的影响分析<br/>——以武夷山为例

不同尺度DEM对面雨量估算模型的影响分析
——以武夷山为例

2020-02-24叶栋水林彬彬

海峡科学 2020年12期

叶栋水林彬彬

(1.福建省气象信息中心，福建福州 350001；2.南京信息工程大学地理科学学院，江苏南京 210044)

1 概述

高时空分辨率的山地降水空间分布对于山体滑坡等自然灾害管理、山区水资源的开发与利用都具有重要意义[1-2]。在宏观的大气环流背景下，山地降水会受地形的影响，存在着气流的动力抬升、降水的再分配以及局地环流等情况，空间分布十分复杂[3-4]。目前，降水空间分布的模拟方法主要有基于气象站点降水数据的空间插值[5]、遥感观测[6-7]、数值模拟[8-9]、再分析[10]等。其中，空间插值法对气象站空间密度依赖性较高，数值模拟存在参数不确定性的问题，遥感观测降水以其较精准的捕捉大尺度降水空间分布能力，得到了广泛应用。但由于遥感降水产品空间分辨率较大，无法满足小区域地形降水对模拟精度的要求，因此国内外学者[11-17]在遥感降水产品的基础上，引入地形因子，提出了各类型的山地面雨量模型，获得了更高分辨率、更精准的山地降水空间分布。

面雨量模型所依赖的坡度、坡向、海拔等地形因子，在不同精细程度的地形下存在差异[18-20]，进而会影响模型模拟精度。这样的地形尺度效应一直以来都是降水模拟过程中的所关心的科学问题。吴昊旻[21]、刘金波[22]、陈跃浩[23]、高学杰[8]等讨论了不同水平分辨率气候模式的精度差异；衣娜娜[24]、黄海波[25]、杜娟[26]等探讨了不同空间分辨率对WRF模拟结果的影响。这些研究均表明，降水的模拟过程对地形分辨率的敏感性较为复杂，在精细的地形下，并不一定获得最理想的降水模拟效果。

不论是气候模式还是WRF模拟，都是对宏观地区降水的模拟方法，所分析的地形分辨率大多为30km、50km等，最精细的也只是讨论了3km、5km以及9km分辨率的地形对降水模拟的影响[24]。若要精细化模拟小区域的山地降水，需要分析更高分辨率的地形对山地面雨量模型的影响。目前发布的1km及1km以内的地形数据主要有1km分辨率的SRTM30_PLUS、500m分辨率的SRTM15_PLUS，90m分辨率的SRTM3，30m分辨率的NGA-SRTM1、ASTER-GDEM-V2、NASA-SRTM1，15m分辨率的SRTM-X-DLR和12m分辨率的ALOS PALSAR。但这些地形数据的空间分辨率不连续，无法使用这些数据来连贯地讨论地形尺度效应对山地面雨量模型的影响。

对此，本文使用二维经验模态分解算法，获取相同分辨率但不同精细化程度的地形，即为不同尺度地形；并以武夷山作为研究区域，分别建立各尺度地形下的山地面雨量模型，初步探索地形尺度效应对面雨量模型的影响，旨在挑选最合适的地形尺度，提高面雨量模型的分辨率和模拟精度，为山地自然灾害管理和山地水资源开发提供更可靠的数据基础。

2 研究方法及数据来源

2.1 研究区域与数据

武夷山脉位于江西和福建边界，是两省水系的分水岭，其东部以丘陵为主，西部和中部以山地为主，地势西北较高，东南较低；山脉呈东北西南走向，长约530km，海拔介于-36m到2153m之间(如图1中的红色边界研究区所示)。该地区属于中亚热带湿润气候，年平均气温在13～14℃，年降水量在2000mm以上，是福建省降水量最多地区。复杂的武夷山脉地形对福建降水具有重要影响，不仅可以阻滞冷空气南移，同时还对暖冷气流强迫抬升，形成显著的区域内地形降水。本文选取24°N～29°N，115°E～120°E中的一块区域作为研究区域，初步探讨地形尺度效应对面雨量模型的影响。

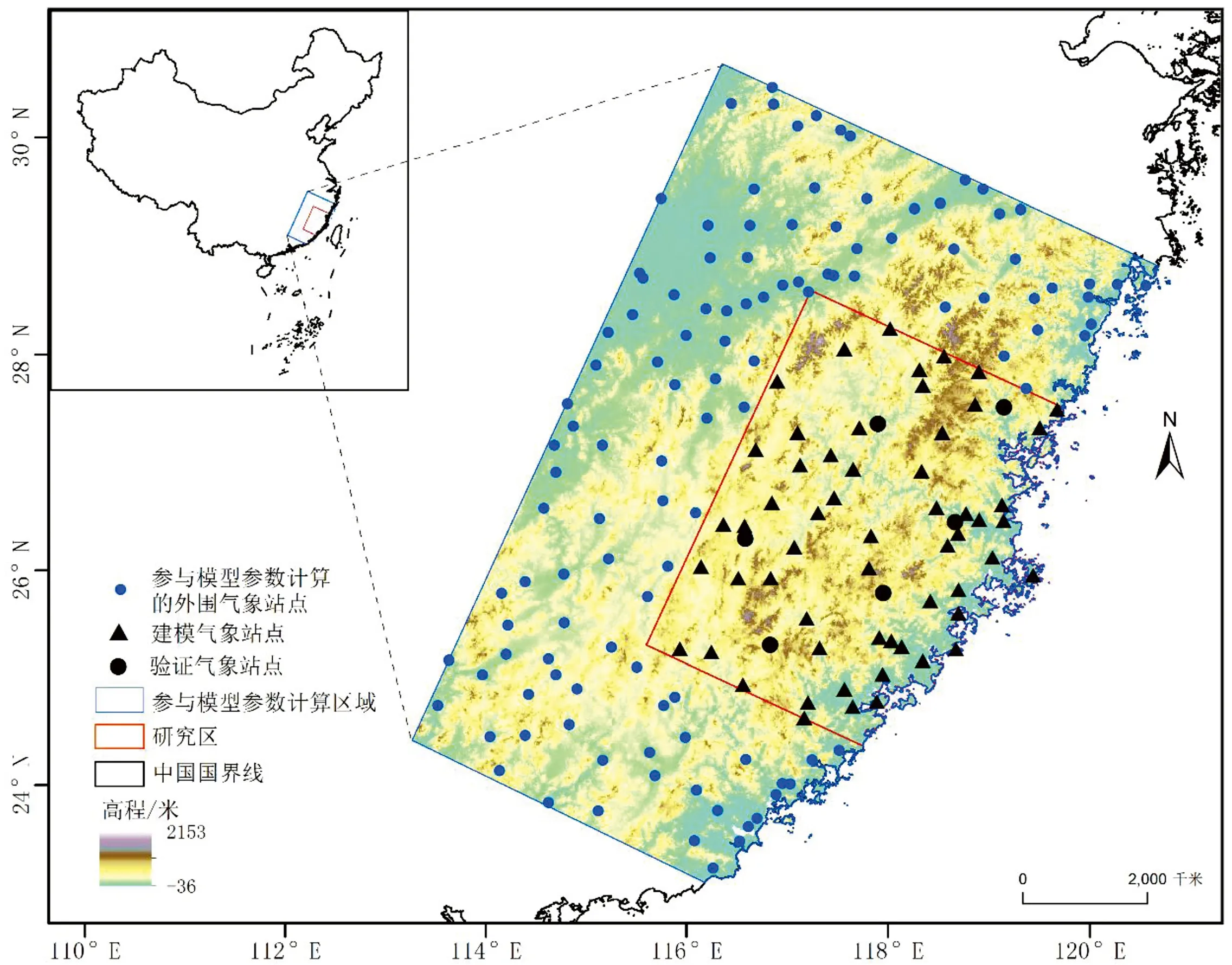
图1 武夷山及周边地区高程及气象站点分布

(1)气象站观测数据。本文使用的2000年至2017年7月份逐日降水数据下载自国家气象科学数据中心(http://data.cma.cn/)，已对数据进行了质量控制，并将日数据累加至月数据。本文共使用175个气象站点的降水数据，其中118个外围气象站点的降水数据只用来辅助计算研究区内63个气象站点的模型因子(主导降水方位)，不参与模型构建和验证统计。另外，研究区内的63个气象站点中，57个气象站作为模拟站点，6个气象站作为验证站点如图1所示。

(2)DEM数据。本文使用的DEM数据为2000年的SRTM(Shuttle Radar Topography Mission)数据，下载自地理空间数据云(http://www.gscloud.cn/)，空间分辨率为90m×90m，采用的投影坐标系为Albers投影(中央子午线为110°，标准纬线分别为25°和47°)。

(3)卫星降水产品。本文使用的2000年至2017年TRMM 3B43V7的7月卫星降水数据，下载自美国NASA(http://mirador.gsfcnasa.gov)，空间分辨率为0.25°×0.25°。

2.2 研究方法

2.2.1 DEM尺度转换算法

经验模态分解(Empirical Mode Decomposition，EMD)是N.E.Huang[27]等人提出的一种数据驱动的自适应非线性时变一维信号分解方法，随后J.C.Nunes等人[28]将其发展为处理二维信号的方法(two-dimensional empirical mode decomposition,BEMD)，在图像降噪、压缩和融合方面有较广泛的应用。BEMD是将原始信号分解成有限个频率从高到低的二维BIMF分量以及每个BIMF所对应的r余量，其中BIMF分量通常为原始信号中不同频率的信号噪声，而余量r为一单调函数，一般为原始信号中不同频率的信号趋势。

从信号学的角度来讲，数字高程模型(Digital Elevation Model，DEM)也可以视为二维的随机信号，高程值即为信号数值，一系列频率从高到低的二维BIMF分量即为地形中的精细部分，所对应的一系列r余量即为由微观到宏观、精细到粗略的地形趋势，即为多尺度地形。设x和y分别是横纵坐标，原始DEM数据为q(x,y)，j为分量BIMF和余量r的标号，N为分解次数，则二维经验模态分解如式(1)所示：

(1)

分量BIMF和余量r的具体计算过程如下：

①初始化：令j=1，g0(x,y)=q(x,y)；

②剥离第j个BIMF分量，并获得第j个r余量：

1)令f0(x,y)=gj-1(x,y)，动态变量i=1；

2)在fi-1(x,y)上进行3×3窗口滑动，计算fi-1(x,y)的局部极大、极小值，组成极大极小值点集；

3)根据极大极小值点集，双线性内插成极大值包络面ti-1(x,y)和极小值包络面bi-1(x,y)，得到平均包络面mi-1(x,y)：

mi-1(x,y)=(ti-1(x,y)+bi-1(x,y))/2

(2)

4)根据公式(3)计算fi(x,y)：

fi(x,y)=fi-1(x,y)-mi-1(x,y)

(3)

5)根据公式(4)计算SD值[23]：

(4)

其中，X为DEM的行数，Y为DEM的列数。

6)SD经验值为0.2～0.3，本文取0.3。若SD<0.3，则代表了精细地形的分量BIMFj=fi(x,y)，代表了宏观地形的余量rj=gj-1(x,y)-BIMFj。若SD≥0.3，则将fi(x,y)看作一个新的信号，并令i=i+1，转至步骤2)，重复执行步骤2)～6)，直至满足终止条件。

本文分解次数N为5，即得到了5个分量r1至r5，分别对应5级尺度地形。包含原始DEM在内，共为6级尺度地形。其地形分辨率均为90m×90m，每个栅格数值的含义均为高程，单位均为m。

2.2.2 面雨量模型

地面降水由空气中的水汽含量、大气运动等大气方面的主导因素和海拔、迎背风坡等地形方面的影响因素共同决定。因此，月面雨量的理论估算模型为P′=P0+P1，其中P0为面雨量模型的趋势项，和大气紧密相关；P1为模型地形项。Zhu等[13]采用海拔高度、坡向、坡度和主导降水方位的函数表达模型地形项，最终得到分站分月面雨量模型，如式(5)所示：

P′=k0P0+k1h+k2cos(PPD-β)·h+k3sin(PPD-β)·h+k4cos(PPD-β)·sin2α+Δa

(5)

其中P′在建立模型过程中，为地面气象站点观测得到的降水量，在根据模型进行面雨量模拟的过程中，P′为所估算的面雨量，空间分辨率为90m×90m；P0为面雨量模型的趋势项，可用卫星降水数据代替，本文采用TRMM 3B43；k1h+k2cos(PPD-β)·h+k3sin(PPD-β)·h+k4cos(PPD-β)·sin2α即为P1模型地形项，其中h为海拔高度；PPD为主导降水方位；β为坡向；α为坡度；k0-4为各项系数；Δa为余项。

PPD是Zhu等[13]提出的用来指示水汽来源方向的参数。其具体计算方法如下：

1)设定A′气象站为目标气象站，其所在位置的坡向为β′(-180°为北，-90°为东，0°为南，90°为西)；设定方位δl为-180°(其方位坐标系与坡向的方位坐标系一致)；

2)搜索A气象站邻近的n个气象站A0～An，计算这些气象站所在位置的坡向β0～βn。计算β0～βn与δl的夹角，将夹角≤90°所对应的气象站归为迎风坡站，反之为背风坡站；

3)统计迎背风坡气象站的平均降水量差DPl；

4)δl按间距Δδ顺时针旋转，重复2)、3)，直至回到-180°。

5)在所获得的DPl集中选取最大值，PPD即为最大值所对应的方位δl。

本文n从3～60分别进行尝试，最终选取40时，最符合水汽来源的自然规律；Δδ选取7.5°。

2.3 技术路线

不同尺度地形的面雨量模型由面雨量模型的地形项和趋势项构成，其中地形项的计算步骤为：①首先，将原始90m×90m空间分辨率的DEM数据按照本文2.2.1所提到的BEMD经验模态分解算法进行多尺度地形转换，得到5级尺度地形r1～r5，并计算得到包含原始DEM在内的6级尺度地形的高程、坡度以及坡向；②融合研究区及周边区域175个气象站点的月平均降水数据，获得6级地形尺度下建模站和拟合站的主导降水方位；③最后根据建模站月平均降水数据以及主导降水方位数据，计算得到面雨量模型的地形项。面雨量模型的趋势项计算步骤为：将空间分辨率为0.25°×0.25°的TRMM 3B43V7数据进行双线性内插，重采样至90m×90m空间分辨率的TRMM数据，该数据即为模型的趋势项。将建模站月平均降水数据、模型地形项、模型趋势项代入模型中，进行建模，每个建模站每月获得一套模型参数。

将建模站的模型参数插值至整个研究区，并根据研究区的地形项和趋势项，模拟得到面雨量。最后，根据拟合站的面雨量模拟结果以及气象观测得到的月平均降水数据，进行模型的验证与精度评价。技术路线如图2所示。

图2 多尺度地形的面雨量模型技术路线

3 结果分析

由于7月水汽充足，降水丰沛，选取7月作为研究月份，并将气象站2000年至2017年7月的降水量取多年平均作为参照数据，反距离加权插值到研究区上，得到气象站观测降水量空间分布图，如图3(a)所示。同样对2000年至2017年7月的TRMM 3B43V7数据取多年平均作为模型的卫星降水数据。由于TRMM 3B43V7数据分辨率较低，无法参与到90m分辨率的面雨量模型中，本文将其双线性内插至90m×90m分辨率，以参与面雨量模型构建，如图3(b)所示。

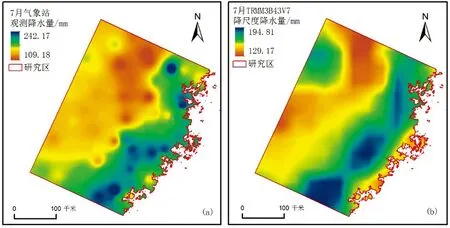
图3 武夷山及周边地区的气象站与TRMM 3B43V7降水量90m×90m空间分布

3.1 各尺度地形

将90m×90m分辨率的DEM作为输入项，根据BEMD算法，分解得到微观到宏观不同精细程度，分别为r1，r2，r3，r4，r5共5个连续变化的地形尺度，如图4所示。图4(a)是最为精细的原始DEM数据，细小的山脉边界都较为明显。r1剔除了原始DEM中最破碎精细的地形，图4(b)代表高程较高的白色区域面积增大，意味着相比于DEM，r1所刻画的山峰被削弱，更多区域被归于山峰。图4(c)中的r2进一步剔除在r1中相对较细小的部分，山脉边界更加柔和。图4(d)中的r3更加粗略，已经只能辨认清山脉主体的形状和走势，山脉边界更加光滑，而图4(e)和图4(f)的r4和r5进一步综合地形信息，r4西南角的两座山峰(白色区域)在r5中已经相连，概化为一座山峰，已经无法呈现山脉的原始形状。从DEM到r1，再逐级到r5，是地形的平滑过程，越往后分解，地形精细度丢失越大，宏观分区趋势越来越明显。另外，从该区域高程的最大最小值分析，随着地形尺度的变大，高程最大值在逐渐减小，最小值逐渐增大，表明地形精细部分在逐渐去除，符合地形尺度转换的信息综合理论，从而证明了BEMD应用于地形尺度转换的可行性。

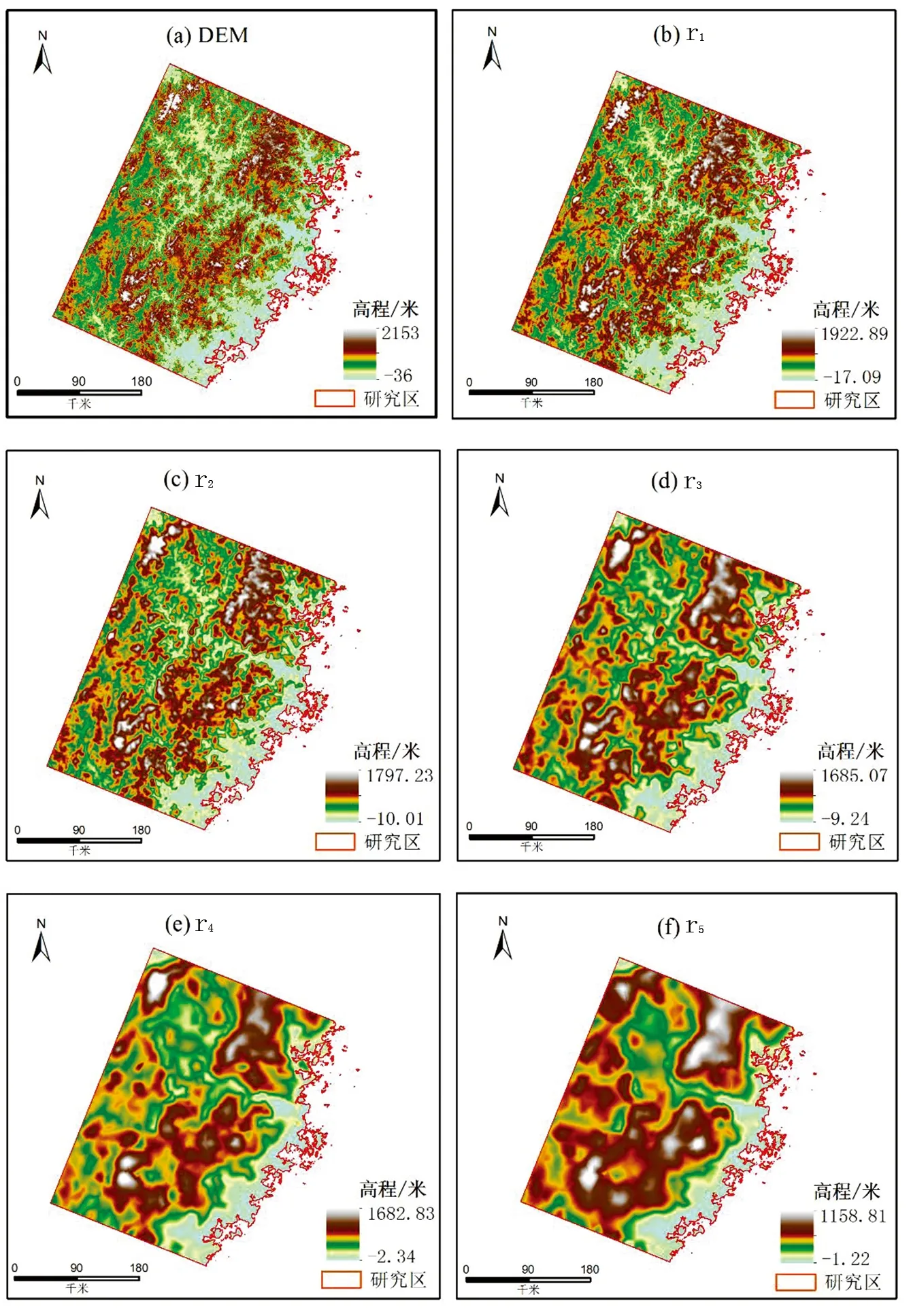
图4 武夷山及周边地区的各尺度地形

为进一步对比各尺度地形下，气象站点所在位置海拔、坡向、坡度三个地形因子的区别，本文还进行了统计，其中坡向的坐标系为：北180°，东90°，南0°，西90°，平地181°。部分气象站的数据如表1所示。

随着地形尺度的增大，精细化程度的降低，每个站点的海拔、坡向、坡度都发生了变化。同一站点在地形尺度的增大过程中，并不表现为单调递增或者单调递减，不同站点的变化规律也不一致。同一站点的坡向在地形宏观化的过程中，会存在较大的变化，甚至在58734站点的DEM向r1转变的过程中，发生了215°左右的变化。这可能是由于所在位置的小山坡在地形转化过程中被概化，其坡向数值从小山坡的坡向变为所在位置的更大尺度的山坡坡向。

3.2 各尺度地形的面雨量模型结果

将BEMD算法所得到的r1到r5地形以及原始的DEM数据作为6层尺度地形数据，分别在各尺度地形下，计算目标气象站周围10个气象站的7月平均降水数据以及所在位置的坡度、坡向和高程，得到该气象站的PPD，从而进一步计算该站的面雨量模型地形项。接着融合TRMM 3B43V7重采样的90m分辨率卫星降水数据，构建目标气象站的面雨量模型。最后，将所有建模气象站的模型参数反距离加权插值至整个研究区，获得研究区各尺度地形的面雨量模型模拟结果，如图5所示。

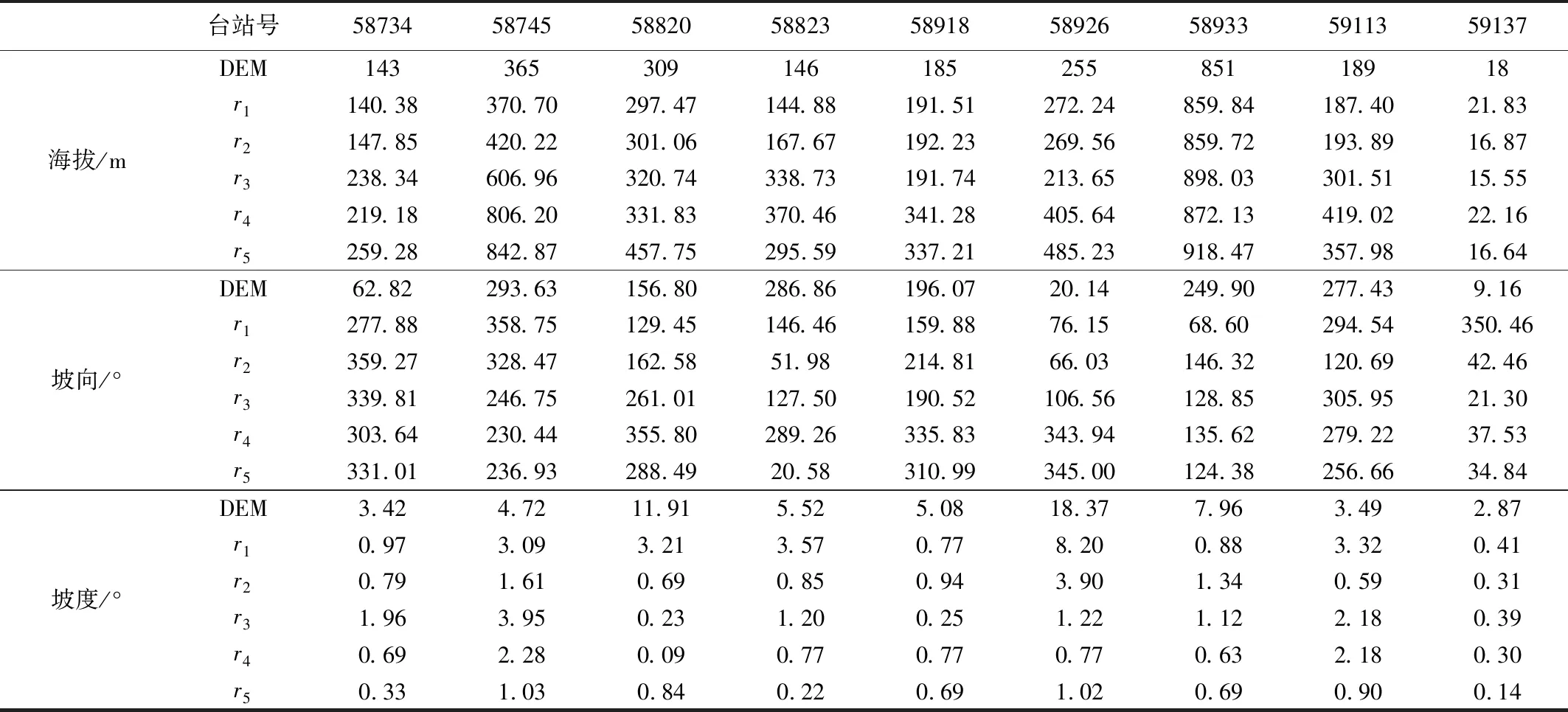
表1 研究区各尺度地形下气象站点的地形因子

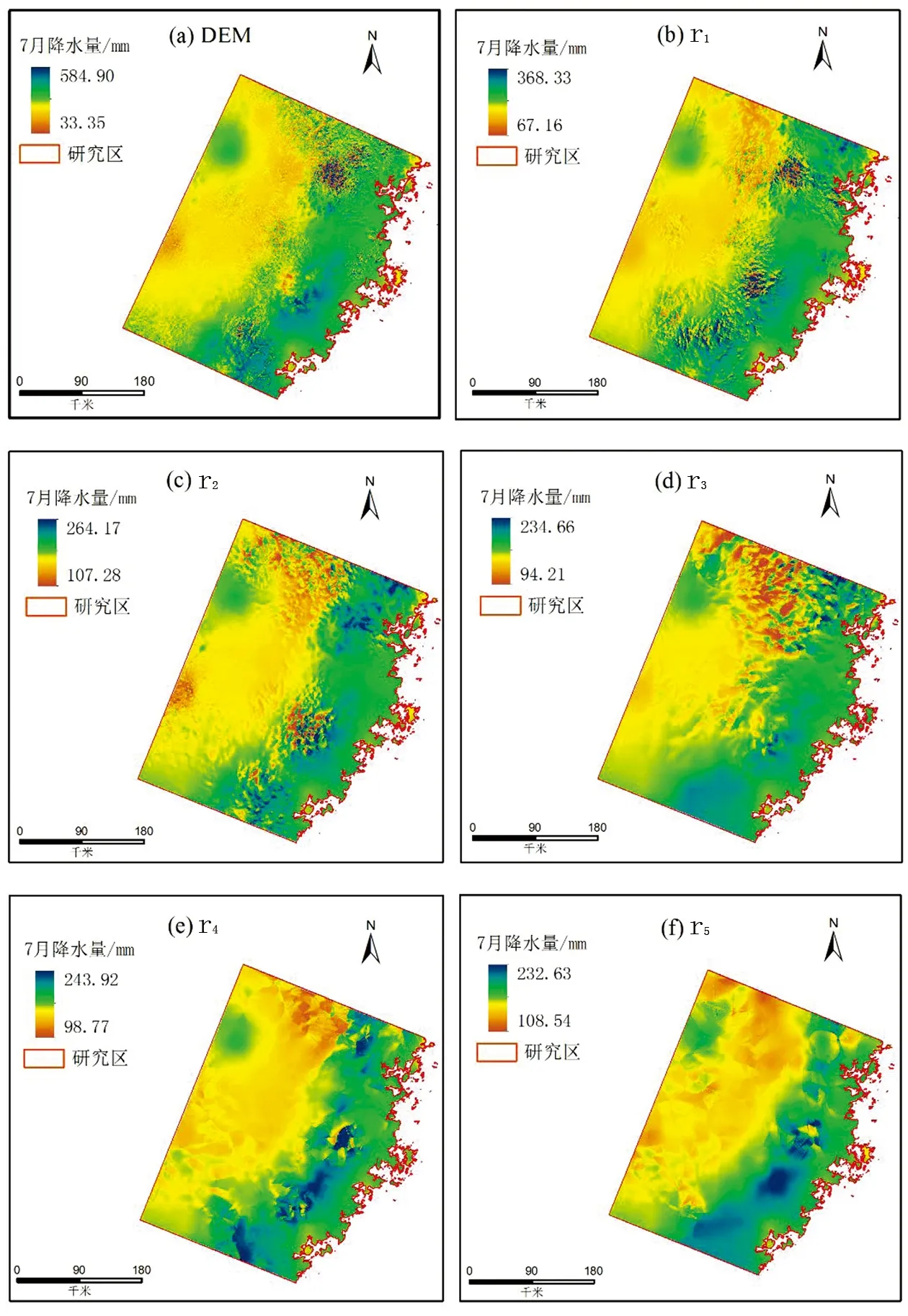
图5 武夷山及周边地区的各尺度地形面雨量模型模拟结果

由DEM以及r1到r5共6个尺度地形构建的面雨量模型模拟结果和气象站插值降水空间分布较一致，并且DEM以及r1到r3相较于气象站插值降水空间分布以及TRMM 3B43V7重采样的结果而言(图3)，模型模拟的降水结果更能体现实际降水存在迎背风坡分布的规律。6级多尺度地形下模拟得到的降水空间分布遵从了多尺度地形的规律，也表现为从微观到宏观、精细到粗略的转变。其中，图5(a)中的DEM模型模拟结果细节最为丰富，可以体现细小山脉的迎背风坡降水量差异。图5(b)中的r1模型模拟结果相较于图5(a)稍微更加粗略，但在东南部，已将细碎的山脉降水分布情况进行了综合，体现为从西南到东北走向的条状分布。r2模型的模拟结果相比于r1，更加综合，东南区域以及北部区域均出现更粗的条带状，山脉的迎背风坡降水差异体现的较为明显。相比于r2模型，r3模型模拟结果对于北部区域的山脉迎背风坡刻画更加综合，但南部山脉的降水空间分布已经趋于均衡，从模拟结果已经无法辨认山脉的走势。从r4、r5模型的模拟结果空间分布上看，已经无法辨认山脉的迎背风坡，只能呈现西北降水量小、东南降水量大的阶梯状降水空间分布。而且，模拟结果均出现由地形信息被过多去除而引起的模型模拟结果偏差，在图5(d)和(f)中表现为几何块状。

除此之外，随着地形尺度的增大，研究区模型模拟得到的降水量最大最小值均不存在单调递增或者单调递减的规律。但DEM模型模拟结果的最大降水量值为584.90，最小降水量值为33.35，相比于气象站插值所得到的最大最小降水量值(图3(a))最大值更大，最小值更少，而且相差较多。而r2和r5模型结果的最大最小值更接近图3(a)，且相比于r5，r2模型结果的空间分布更接近图3(a)。

3.3 面雨量模型最优尺度地形选择

对未参与建模的6个验证气象站点进行误差分析，统计得到各尺度地形面雨量模型验证站点的误差统计量[12]：相关系数r2，平均相对误差MRE和均方根误差RMSE，误差情况如表2所示。

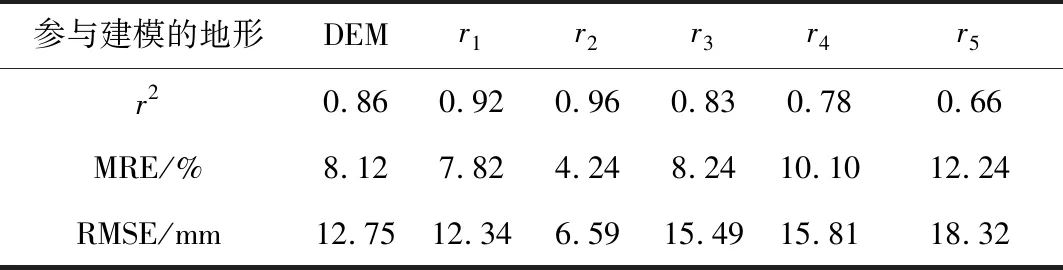
表2 不同尺度地形面雨量模型验证误差评价指标

由表2可知，r1和r2面雨量模型对武夷山及其周边地区7月份降水量模拟效果较好，相关系数均在0.90以上，r2面雨量模型精度最高，相关系数达0.96，r1次之。DEM、r3、r4和r5面雨量模型的相关系数均在0.9以下，相比于r2，下降了至少10.4%。DEM、r3、r4和r5面雨量模型的MRE和RMSE明显增大，MRE均高于8%， RMSE均超过12.5mm，其中r5模型误差最大，MRE、RMSE分别达到12.24%、18.32mm。结果表明，r2模型的模拟效果最优，r1模型略次，DEM、r3、r4和r5模型效果依次下降。

结合统计结果和图5可知，DEM模型模拟结果的降水量最大最小值较极端(图5(a))，这与模型所依赖的地形尺度直接相关。DEM为最精细的地形尺度，对细小的山脉均刻画淋漓尽致。但对于面雨量模型而言，过于精细的地形不但不会提高模型精度，反而会给模型带入噪声，从而降低了模型精度。同样，相比于尺度更小的r1模型，r2模型虽然基于更大尺度的地形，但精度更高。相比于r2模型，r3面雨量模型的模拟结果精度降低，这表明在r2至r3的变化过程中，对于降水空间分布具有重要意义的地形信息在综合过程中被去除，从而影响了模型精度。在重要地形信息的不断去除过程中，r4、r5模型模拟结果精确度逐渐下降。

为了更直观展示以上验证结果，将各地形尺度面雨量模型估算值和气象站点观测值绘制成散点图，如图6所示。

图6 验证站的各地形尺度面雨量模型估算值和气象站观测值散点图

由图6可知，6个尺度地形的面雨量模型估算的月降水普遍比气象站观测的月降水高，但其中有一个站点降水估算均过低，这表明不同尺度地形面雨量模型在同一站点的预测上，存在一定的规律性。另外，DEM、r1模型在150mm以下的降水量估测中劣于r2模型，这是由于150mm以下的降水量主要集中于西北山区，而这块区域的地形相较于东南部分更加起伏，地形对降水的影响更大。对于这块区域而言，地形尺度的改变对其影响较大，精细的DEM不仅不会提高模型精度，反而会加入噪声，影响模型的准确性。综上所述，各尺度面雨量模型中，r2尺度地形不仅最大程度规避了会产生噪声的地形细节，而且保留了对面雨量存在影响的地形信息，对武夷山及其周边地区7月份月降水量模拟的准确性表现最优。