基于多因素分析的铝焊接用焊剂组分优化方法*
2020-02-24赵红波王璟丽席敏敏编译
赵红波, 王璟丽, 赵 勇,席敏敏, 刘 斌, 李 靖 编译
(1. 国家石油天然气管材工程技术研究中心, 陕西 宝鸡721008;2. 宝鸡石油钢管有限责任公司, 陕西 宝鸡721008;3. 北京隆盛泰科石油管科技有限公司, 北京100101)
0 前 言
产品加工制造技术的规模化已经成为推动汽车产业创新和进步发展的主要因素, 在材料领域, 影响汽车制造技术的是金属材料, 在所有金属材料中, 铝对汽车生产制造具有不可替代的价值。 焊接作为一种将两块或多块金属永久连接的加工工艺, 成为影响产品制造的主要因素。 目前, 对于铝焊接研究的主要方向是获得良好的焊接质量及相应适合的焊剂材料的开发。 作为生产应用中普遍存在的金属材料, 铝几乎与所有技术开发和研究领域都有着密切联系, 因而促使焊接铝所用的焊剂材料也得到了普遍的应用。 作为铝焊接过程中一种非常有用的保护剂, 焊剂能有效去除铝表面由于暴露在空气中而产生的AlOH层。 焊接前或焊接中, 如果对氧化铝层不能及时清理 (除非将它的含量降低到最低), 所形成的夹杂物将极大程度地影响焊缝质量。 因此掌握适用于铝焊接用焊剂的特征、 化学成分、 形态特征以及铝和其合金的可焊性具有相当重要的意义,通常采用多物理分析方法对铝用焊剂进行研究。对于铝的焊接, 不管采用任何一种焊接方法都需要了解铝用焊剂最佳的成分配比。
Achebo 和Ibhadode 研究发现, 铝焊缝的抗拉强度值越大, 焊缝质量越好。 鉴于此, 本研究以强度性能作为确定焊剂成分的标准, 结合焊剂组分中不同活泼元素的置换情况, 并依据专业的估算方法, 采用Hadamard 矩阵和田口试验优化设计方法提出了一种最佳的焊剂成分,在以上研究基础上, 对试验设计方法的效率进行了对比分析。
1 四变量Hadamard 矩阵设计方法
两水平多变量分析IV Hadamard 矩阵方法是基于两水平4 个试验因素的设计, 其中, 4 个变量 (A、 B、 C、 D) 中的每一个因子均有一个高水平和低水平值。 不管成分和变量数目的多少, 所有设计方法中焊剂的不同变量之间的主要作用需要提前掌握、 计算或估算。 本研究确定的铝焊剂的化学成分见表1。
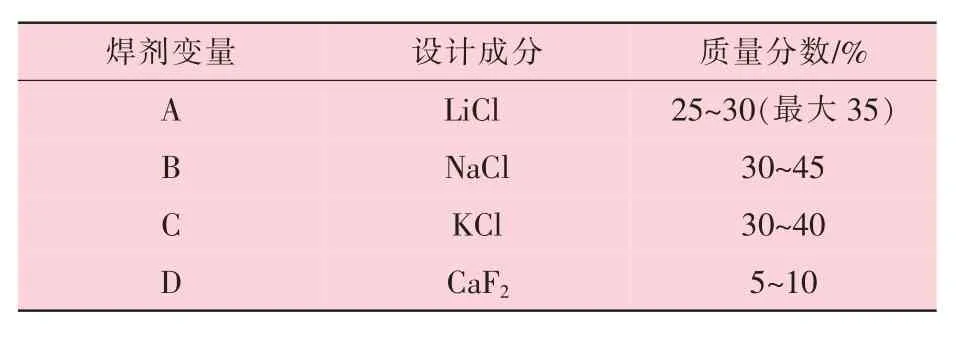
表1 铝焊剂的化学成分
采用Hadamard 矩阵设计的变量组合见表2,A、 B、 C 和D 为变量, 矩阵中的变量按照表1成分范围确定, 其中, 表2 中注明 (+) 取值为焊剂成分范围的高水平值, 注明 (-) 取值为焊剂成分范围的低水平值; 第4 个变量D 在配方确定过程中被优先考虑, 另外的变量A、 B、 C填入第1~3 列, D 变量预留列为空白。

表2 四变量Hadamard 矩阵设计
以表1 所给定的焊剂成分为基础, 依照表2四变量Hadamard 矩阵设计, 以焊剂配方的最终质量分数和相加需为100%为准则, 设计提出了8种焊剂初始配方的化学成分, 具体见表3。 采用8种焊剂分别进行焊接, 每种焊缝按照联邦检测标准《材料检测方法要求—FED-STD-151》 加工成5 个应力检测所需的标准尺寸试样, 并进行抗拉强度检测, 其平均抗拉强度见表4。

表3 8 种焊剂初始配方的化学成分

表4 8 种新焊剂焊接件焊缝金属的平均抗拉强度
依据主变量为焊剂材料的组分元素, 这里的抗拉强度由每种焊剂组分确定, 由此进一步确定出主要变量对焊缝强度的影响情况。 对应表1 主要变量 (焊剂组分), 按照xAhigh-xAlow公式对焊缝强度的影响作用进行计算可得: A 组元为17.75; B 组元为15.75; C 组元为-4.75; D 组元为-9.75。
在上述所得值的基础上, 按公式 (1) 计算表2 中5、 6 和7 变量的差值。

其中, T 表示试验焊剂个数 (T=8), i 代表差值编号 (如i=5, 6, 7), 应用公式 (1) 计算出各变量的差值见表5。

表5 各变量差值的计算结果

1.1 检测标准的确定
3 个自由度的选定值为φ; 这里α = 0.05,在95%置信水平; tβ= 2.35 (tβ是在σ2不确定的情况下, 从t 分布单边表的概率分中获得)。 N高=N低, S=29.95, 将结果带入公式 (2), 计算结果为49.77。

1.2 检测结果所需条件
如果平均值作用是正向的, 取低水平值μlow更好; 如果平均值作用是负向的, 取高水平值μhigh更好。

1.3 结果处理
由以上所确定的选定值为条件, 并参照以上检测方法, 统计推导出最终的成分含量为A=30%、B=45%、C=30%和D=5%, 经计算这些百分含量相加总和为110%。 如前所述, 需使组元质量百分比相加总和为100%。 针对以上, 对各元素含量采用平均值来进行了修正, 参照表1 确定的成分范围, 低于平均值的值认为是在较低的范围内, 高于平均值认为是在较高的范围内, 反复采用这个方法使变量组合的临界值不超过100%, 最终采用此方法获得最优的成分组合为A (27.5%LiCl)、 B (37.5%NaCl)、 C (30%KCl)和D (5%CaF2)。
采用确定的焊剂组分进行焊接, 将焊缝按标准要求制备成拉伸试样, 经检测所得抗拉强度为316 MPa, 由此证实该测试应用模型的可靠性。
2 田口法
田口法是日本田口玄一为了提高产品生产质量而总结形成的一种质量工程方法。 该方法采用一个特殊的正交数组设计方法, 仅通过很少的试验数据就能达到对于整个工艺参数的研究, 本研究采用田口法预测了铝焊接用焊剂的最佳组合。
参照表1, 采用田口法试验布局的自由度为7 的L8(24) 正交数组。 当采用L8正交数组时,试验采用8 种工艺, 相应的试验布局见表6。

表6 L8 (24) 正交数组下的试验布局情况
同样采用表6 中每一种组分焊剂焊接5 道焊缝, 对每个焊缝进行拉伸试验检测, 8 种焊剂组分下焊接件焊缝金属的平均抗拉强度见表7。

表7 8 种焊剂组分下焊接件焊缝金属的平均抗拉强度
依照焊缝的抗拉强度值越大, 焊缝质量越好准则, 由公式 (3) 可得, 损失函数越大, 焊缝质量性能越好。列出的相一致的S/N 信噪比确定。

将表8 中列出的值代入焊剂成分组分变量及水平中, 得到表9 的结果。
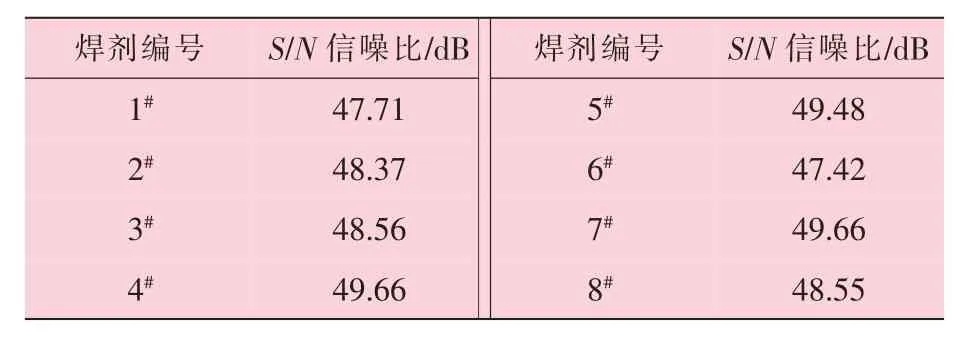
表8 与抗拉强度结果相关的S/N 信噪比

表9 不同焊剂组合下S/N 信噪比汇总
由表9 可见, 最佳焊剂成分为A2、 B2、C1、 D2, 得到成分组合为30%LiCl、 45%NaCl、30%KCl 和10%CaF2。 遵循成分组合质量百分比100%原则, 采用如前所述的方法修正得出焊剂最终成分组合为: 27%LiCl、 37%NaCl、 30%KCl和6%CaF2。
由表9 可见, 当水平值改变时, 相差较大的参数对可焊性产生较大的影响。 研究可见, 参数B的差值最大。 图1 为焊剂设计的S/N 信噪比, 图中红线为S/N 信噪比总平均值。 Esme 认为百分比大小表示一个因素减少变化的相对能力。 对一个高百分含量的因素, 一个很小的变化将对焊缝性能产生很大的影响。

图1 S/N 信噪比
表10 列出了表9 中S/N 信噪比ANOVA 结果。公式(5) ~(7) 用于得出S/N 信噪比的平方和。其中公式(5) 和(6) 由Berginc 等人提出, 即

式中: Ts——所有结果的总和;
N——结果数量;
CF——校正系数。
同时, Scheaffer 和McClave 也提出公式(7),主要用于确定焊剂每种组元的平方和, 即

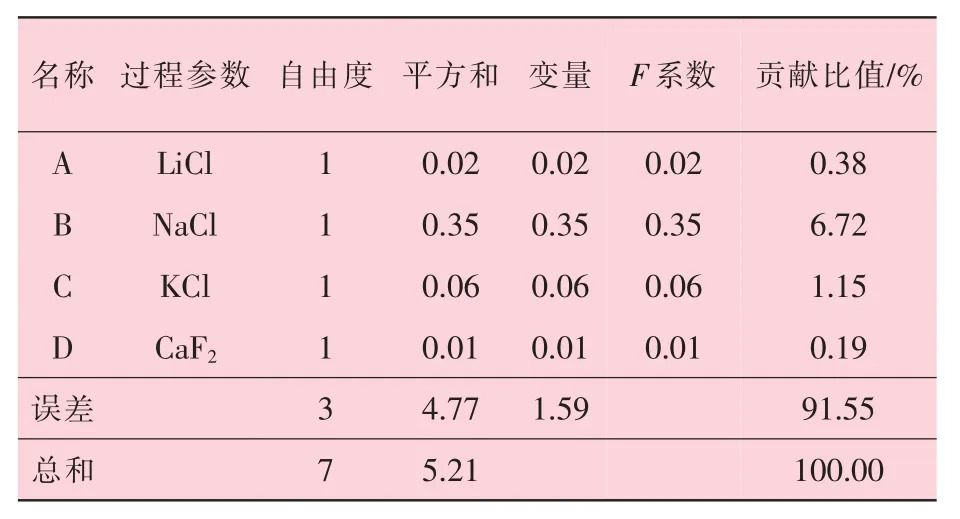
表10 最优焊剂组分S/N 信噪比例变量统计分析结果
由表10 可见, NaCl 为铝焊剂主要影响因子, 贡献比值作用最大, 达到6.72%; 其次是KCl, 贡献比值1.15%, 而LiCl 和CaF2贡献因子较低, 分别为0.38%和0.19%。
对本次试验中所得研究成果, 采用确定的最优配方进行焊接试验, 并检测焊缝力学性能。 在这里S/N 信噪比作为对焊缝性能影响最大的变量, 常用来预测、 判定焊剂性能及性质的提高情况。
S/N 信噪比的预测采用公式 (8) 中η 最优化组分或者水平来确定得到, 即

此处的ηm是S/N 信噪比的总平均值, η 表示最佳水平下的S/N 信噪比的平均值, n 是对焊接性能具有显著影响的主要参数数量值。 应用公式(8) 所确定的结果如下:
对于焊剂组分配方A2B2C1D2 来说
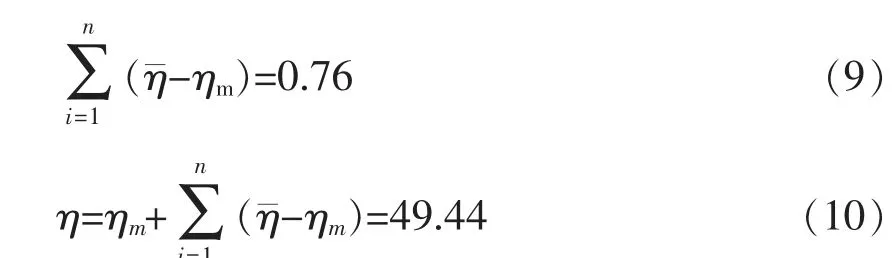
对于确定出焊接过程中的现有焊剂组分配方A1B1C2D1 来说

对于A2B2C1D2 也采用与上述相同的计算方法, S/N 信噪比值的增长表明, 同一合金元素实际焊接后的焊缝化学成分比采用预测工艺参数所得的含量更大。 优选焊接参数验证试验结果及预测过程相比较结果见表11。
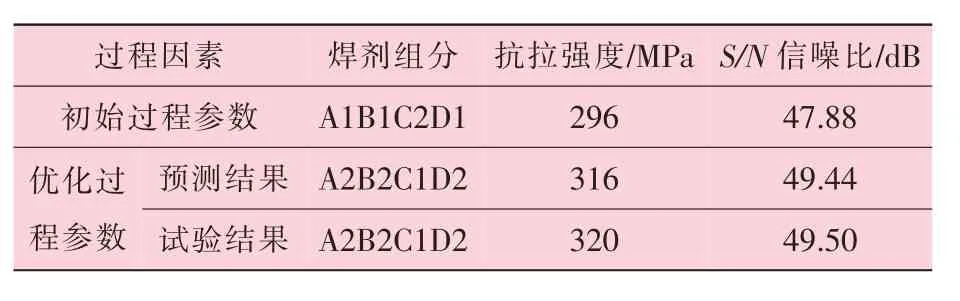
表11 验证试验检测结果
对初始焊接参数优化后的S/N 信噪比提升了1.62, 使抗拉强度增加了1.08 倍, 由此可见, 采用田口分析方法可使抗拉强度得到显著提高。
3 结果讨论
通过采用Hadamard 多元化学成分法和田口法对焊剂组分优化设计进行了研究。 结果表明,Hadamard 多元法能产生多个焊剂组分, 同时, 在焊剂组分确定过程中, 一个变量与另一个变量关系密切, 采用该方法确定的焊剂组分为30%LiCl、45%NaCl、 30%KCl 和5%CaF2, 其质量百分数大于100%。 为了使其质量百分比达到100%, 对焊剂组分进行了改进, 形成新的焊剂组分: 27.5%LiCl、37.5%NaCl、 30%KCl 和8.5%CaF2, 该焊剂组分所焊焊缝的抗拉强度最高值为316 MPa。
田口法同样也被用来优化焊剂成分, 通过此方法确定焊剂成分, 30%LiCl、 45%NaCl、 30%KCl和10%CaF2。 对其进行修正, 最终确定焊剂成分:27%LiCl、 37%NaCl、 30%KCl 和6%CaF2。 这种焊剂焊接后所得焊缝的抗拉强度为320 MPa。
在以上优选的焊剂成分、 组分配方及不同研究人员的研究基础上, Varley 在本研究中提出了一种特殊的铝焊接用焊剂组分, 30%NaCl、 28%KCl、26%LiCl 和16%NaF2。 Glizmaneko 和Yevseyer 对于铝焊接用焊剂也提出了新的组分范围, 即0~30%LiCl、 0.6%KCl、 5~15%KF、 剩余量为NaCl。Davies 提出了组分范围为0~30%LiCl、 0.6%KCl、5~15%KF, 剩余量为NaCl。 Manfredi 等人提出焊剂 组 分 为70%NaCl、 28%KCl 和2%CaF2。 但Utigard 等人却提出了47.5%NaCl、 47.5%KCl 和5%氟化盐铝焊剂组分。 另外, 研究者通过对铝焊剂焊接所得焊缝金属进行拉伸性能检测, 得出焊 缝 抗 拉 强 度 范 围 在298 ~434 MPa; Ellis 和Padmanabham 检测得出焊缝抗拉强度范围在255~334 MPa; 并且Achebo 和Ibhadode 对焊缝金属进行拉伸性能检测, 得出焊缝抗拉强度为310 MPa。Weston 通过研究2219 和5083 铝合金焊缝, 发现此类合金焊缝抗拉强度为270 MPa 和297 MPa。Yoon 也同时研究6061 铝合金, 发现这类合金的抗拉强度为200 MPa。 Palmer 等人研究6061-T6铝合金的拉伸性能, 发现这类合金的抗拉强度为310 MPa。 同时, 他们通过对6061-0 合金研究得出一致的强度值为117 MPa。
由此可见, 通过采用Hadamard 矩阵设计方法及田口优化法修正所得最佳焊剂组分, 都在其他研究者设定的焊剂配方范围之内, 同样也适用于它们的抗拉强度值。 由此可以确定, 本研究所确定的方法可以满足不同研究者的需求, 并具有较好的实用性和参考价值。
4 结束语
在焊剂组分确定过程中, 有不同比例选择的多种方法, 采用Hadamard 多元法与田口法优化确定出了新的焊剂组分, 并通过修正使新焊剂组分质量百分比总和为100%。 Hadamard多元法与田口法应用简单、 容易, 采用此两种方法优选形成的焊剂组分最终可得到最高的抗拉强度值。 两种方法的不同之处在于,Hadamard 多元法最终可以确定出不同组元及成分之间的相互作用, 由于很多焊剂在生产制造过程中具有相当宽泛的成分范围, 对于研究者来说, 通常需要采用大量的焊接试验, 才能将成分缩小到最佳的范围之内; 田口法对于焊剂的成分研究及修正具有很好的实用性和可操作性, 但缺点是田口法在某些方面具有一定的不可靠性。
通过最佳焊剂组分的确定, 证明了多物理量分析方法及田口法使用的相关性, 从而为焊剂研究提供了参考。
