棒束通道中燃料棒壁面温度的子通道分析

2020-02-23沈丹红傅孝良

核科学与工程 2020年6期

沈丹红，董博，杨婷，傅孝良，程旭

(1.上海交通大学核科学与工程学院，上海 200240；2.中国核动力研究设计院核反应堆系统设计技术重点实验室，四川成都 610213；3.国家电投集团科学技术研究院有限公司，北京 102209；4.国家能源核电软件重点实验室，北京 102209；5.上海电力大学自动化工程学院，上海 200090)

在反应堆设计和安全分析中，堆芯中冷却剂的流动和传热情况至关重要。燃料组件中最常用的结构是棒束结构。冷却剂流经棒束间的通道带走由棒束产生的热量，从而保证燃料棒四周的温度不超过其限值。因此，增强或者改进燃料棒与冷却剂之间的换热能力成为反应堆热工水力设计的重要任务。

子通道程序是目前应用较为广泛的安全分析和热工水力计算程序[1]。与单通道模型不同，子通道模型考虑了相邻通道间质量、能量和动量的横向交换。这种考虑使热通道的冷却剂温度比未考虑横向交混时有所降低，相应的燃料元件的表面温度与中心温度也略有降低。因此，子通道方法提高了热工设计的准确度和反应堆设计的经济性。

目前，国内外已有大量可用于反应堆热工水力计算的子通道程序[2-5]。本文选用COBRA-Ⅳ程序[6]对棒束中燃料棒表面温度进行了模拟，并根据比对结果对换热模型和空泡份额模型进行了分析。

1 实验工况及子通道建模介绍

本文所选实验数据来源于棒束内流动与传热行为试验[7]。试验棒束为5×5正方形排列棒束，如图1所示。25根加热棒外径D=9.5 mm，棒中心距P=12.6 mm，矩形通道截面尺寸66.1×66.1 mm。试验段发热长度2785 mm。自入口每隔相等距离安放一个定位格架，共6个，格架形式为普通格架，阻塞比为0.24。

图1 棒束通道横截面尺寸示意图Fig.1 Cross sectional of the rod bundle

由图1棒束通道的横截面可以看出，棒束的排列具有对称性，故仅取横截面的四分之一进行子通道计算。子通道的划分如图2所示，共九个通道，九根燃料棒。其中，3号、6号、7号、8号为完整燃料棒的二分之一，9号为完整燃料棒的四分之一。本文中均以5号棒为研究对象进行计算值与实验值的对比。子通道输入卡的相关参数如表1所示。

图2 子通道的划分Fig.2 Cross sectional of sub-channel division

表1 子通道输入卡的相关参数Table 1 Parameters of sub-channel input

根据实验中的流动工况，本文对不同压力、不同热流密度和质量流量的棒束流动进行了计算。表2中分别列出了单相和两相工况下的子通道入口边界条件的大致范围。其中，单相工况12个，编号为D01至D12；两相工况18个，编号为L01至L18。

表2 不同工况的入口边界条件Table 2 Inlet boundary conditions for different working conditions

2 单相工况计算结果分析

为了较为准确地对燃料棒壁面温度进行模拟，需要选择合适的对流换热模型来正确模拟燃料棒壁面与冷却剂流体之间的换热。由于现阶段对于流体纵向流过棒束时换热特性研究较少，在一般计算中，仍按照普通圆管的换热公式进行计算，并将棒束通道的当量直径取为特征尺寸。其中，最为常用的是Dittus-Boelter关系式(简称D-B公式)，如公式(1)所示，为子通道程序中所用D-B公式：

Nu=0.023·Re0.8·Pr0.4

(1)

对于棒束通道而言，不同研究者提出了关于D-B公式的修正形式。如公式所示，Weisman[8]提出了流体是水时的计算公式：

Nu=C·Re0.8·Pr1/3

(2)

式中：P——燃料棒中心距,mm；

D——燃料棒直径,mm。

在本文的算例中，P=12.6 mm，D=9.5 mm，故C=0.031 7。

分别应用D-B公式和Weisman公式，对单相的十二个工况进行计算。每个工况中，分别计算两个公式在子通道中的计算结果与实验值的误差，并求平均，做出不同工况下的计算误差分析图，如图3所示。

图3 单相各工况平均误差分析Fig.3 Average error of single-phase operating conditions

图3所示的十二个工况中，Weisman公式的计算误差小于D-B公式的情况共有八个，可初步判断选用Weisman公式得到的计算结果更好。另选取D02和D05这两个工况进行分析，如图4所示。

图4 单项工况计算结果对比图Fig.4 Comparison of calculation results in single phase conditions

由图3的误差分析可知，D02和D05这两个工况中，两个公式所得计算误差均较其他工况偏大。D02工况中，两个工况均有部分点与实验工况较为吻合，而总体上看D-B公式的趋势与实验值更接近，故该工况下D-B公式平均计算误差更小。在D05工况中，两个公式计算所得结果与实验值相比均较高，而使用Weisman公式所得结果更接近实验值。与其误差结果相似的D09工况中，也是如此，在计算结果偏离实验值较远时，使用Weisman公式可以得到更为接近实验值的结果。

综合以上分析，在本文进行的计算范围内，与D-B公式相比，选用Weisman公式进行计算能够在整体上获得更好的计算结果。

3 两相工况计算结果分析

3.1 两相换热模型

在两相流动中，冷却剂与壁面之间的换热情况非常复杂。在进行模拟计算时，不仅要判断冷却剂的换热工况，还要给出各个工况下合适的换热模型。在较早版本的COBRA程序中，两相换热系数完全由用户提供[9,10]。但在目前的COBRA程序中，有一个来源于RELAP4的公式包可供选择[11]。

选用该公式包进行计算时，程序会根据壁温、空泡份额等条件判断冷却剂的换热工况，从而选择合适的换热公式。表3列出了该公式包所划分的七个流动区域及相应的换热公式名称。

表3 COBRA中的两相换热公式[11]Table 3 Two-phase heat transfer equations in COBRA

以工况L01为例，如图5所示，实线为选用RELAP4公式包所算得的壁面温度变化。结合该公式包的判断标准，对该曲线解读如下所示。

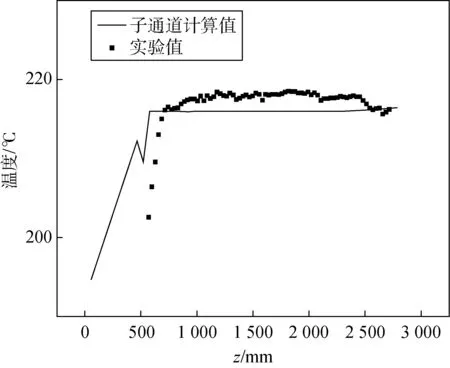
图5 RELAP4公式包计算所得壁温变化对比图Fig.5 Comparison of wall temperature calculated by RELAP4 formula package

(1)在壁面温度达到饱和温度之前，程序判定为强制对流阶段，默认采用D-B公式进行计算。通过对单相结果的分析，本文中均采用Weisman公式进行计算，故此阶段所用公式为单相时的换热公式，即本文所选Weisman公式。

(2)壁面温度达到饱和温度之后，换热公式采用Thom提出的换热模型[12]，如公式(3)所示：

(3)

式中：ΔTsat——壁面温度与流体饱和温度的差；

q——热流密度;

p——系统压力。

公式(3)计算所得温度差为华氏度单位。由该公式可以看出，此时壁面与流体间的换热仅与热流密度和压力有关，在此工况下为定值。由计算结果也可看出，此时壁面温度不变化，该公式无法模拟出定位格架的效应。

(3)壁面温度变化的后半段，有所升高，此时不再使用Thom换热模型。当空泡份额大于0.8时，换热模型改换为Schrock and Grossman模型[13,14]，如公式(4)至公式(6)所示。

(4)

(5)

(6)

该模型虽可以模拟定位格架效应，但计算结果与实验数据不符，说明对于流动区域的判断有误。而该判断准则是依据空泡份额的大小来进行流动区域的判定的。因此，对于空泡份额的相关计算模型需要进行改进。

3.2 空泡份额模型

空泡份额α是两相流的基本参数之一，由于它的测量比较困难，因此必须借助空泡份额的关系式进行计算。在上一节所示的计算中，选用的空泡份额模型为均相模型，其结果显示该模型并不适用于此工况的计算。为了找到合适的空泡份额模型，用COBRA程序中的几个模型分别进行计算，并将模型的具体形式列如表4所示。

表4 空泡份额模型公式[15]Table 4 Correlations of void fraction model

表4所列公式中，vG、vL分别为汽相和液相的流速，x为质量含气率(0≤x≤1)，S为滑速比(S>1)。通过对公式的简单分析可知，同一工况下，用均相模型计算所得空泡份额数值最大，其余两个模型计算结果较之稍小。

仍以工况L01为例，用不同模型计算所得空泡份额变化如图6(a)所示，所得壁温变化如图6(b)所示。

图6 不同空泡份额模型计算结果对比Fig.6 Comparison of different void fraction models

由图6(a)可看出，与从公式进行分析得到的结论相同，均相模型得到的计算结果数值最大，Slip模型所得结果随滑速比S的增大而减小。S=3.0时的Slip模型和Modified Armand模型所得结果较小，然而两者所得空泡份额数值变化趋势不同，A05所得结果最终未超过0.8，而其余几组结果均在不同位置空泡份额的数值超过了0.8。根据RELAP4公式包的判断准则，当空泡份额超过0.8时，不再使用Thom换热模型，而选择Schrock and Grossman模型。故在图中所示的计算所得壁温有着不同的变化趋势。其中，与实验值吻合最好的计算结果为A04，A05，相对应的空泡份额模型分别为Slip模型和Modified Armand模型。由于使用Slip模型时，在不同工况下选用精确的滑速比是较为困难的，故本文最终选用Modified Armand模型进行计算。

3.3 两相计算结果

对两相的十八个工况进行计算，并选择其中三个工况为一组进行分析。如图7所示，分别为工况L15、L01和L08。这三个工况质量流率和热流密度一样，压力分别为1.5 MPa、2.0 MPa和4.0 MPa。

图7 两相工况计算结果对比图Fig.7 Comparison of calculation results in two phase conditions

由图7可以看出，在本文所涉及的两相工况下，壁温上升到一定温度后保持不变。计算所得壁温较实验值更早的出现这种变化。这是由于在单相部分，计算值均略高于实验值。这使得计算所得壁温较早的达到饱和温度，换热模型由单相换热模型变为Thom换热模型，同一工况下，由该模型计算所得壁温为定值。

对计算结果进行误差分析，上述L15、L01、L08工况下的平均误差分别为0.79%、0.89%、0.86%，可见Thom换热模型对于压力这一参数的变化并不敏感。由于两相工况下的误差一部分来源于单相换热模型，一部分来源于Thom换热模型，且单相换热模型的误差更大，因此平均误差的分析对于Thom换热模型而言意义不大。Thom模型主要影响了两相阶段计算值与实验值的偏差，所有工况所得计算结果与实验值的温度差均不超过10 ℃，误差小于5%，计算结果及对比图不在此一一列举。

综上，两相工况下选用RELAP4公式包进行换热模型的选择。空泡份额作为公式包进行状态判断的重要参数之一，需要选择合适的模型对其进行计算。经过对比，本文选择Modified Armand模型计算空泡份额。两相换热模型中的Thom换热模型能够得到较好的换热结果。但单相换热模型对两相计算仍有较大影响，需要进一步改进单相换热模型。