电流热过载保护在非电机专用微机保护装置中的运用

2020-02-23

中国新技术新产品 2020年24期

（中国石化燕山石化公司，北京 102435）

0 引言

异步电机将电能转换为机械能，在该过程中损失的能量主要转换成热能，并向周围冷却介质扩散。绝缘扩散不及时就会形成热积累，从而损坏绝缘，导致电机绝缘受损不可恢复。因此，热积累会造成电机绕组绝缘特性下降，缩短电机的使用寿命。绝缘材料在规定的容许温度下工作，可以获得理想的使用寿命。当绝缘材料超过容许温度时，绝缘材料的使用寿命将会呈指数急剧降低[1]。

总的来说，电机电流热过载保护对电机的使用寿命至关重要。目前电机热保护主要包括以双金属片为核心元件的热继电器、定子埋入测温电阻以及微机热保护等。各类热保护的原理和效果不同，应用场景也不同。其中，微机热保护充分借助微积分数学工具、采用电机热保护模型，最大限度地接近热积累的实际过程，是最主要的电机热保护装置。当前，最常见的电机专用中压微机保护装置包括SEL749M、ABB REM615等。

由于各种因素，很多电机的中压微机保护装置采用非电机专用的综保，其没有电机热保护模块，也不具备电机热保护功能。现有的解决方法主要采用在热曲线上取1个定点数据做定时限保护，该方法严重背离热积累的过程，不能实现电机热保护的功能。

1 电机电流热等效原理

电机作为非均质物体，要衡量其发热的程度应该取其最高温度，但电机是不规则物体，计算其最高温度十分困难且结果不准确。因此，在热保护计算工程的应用中，假定电机是1个均质物体，只计算它的平均温升，其发热过程就得以缩短。根据能量守恒原理，电机的热平衡微分方程,如公式（1）所示[1]。

式中：Pdt为在dt时间内电机总的发热量，J；cGdτ为电机的蓄热量（其中G、c和dτ分别为电机的重量、比热和dt时间内的温升变化值，℃）；aSτdt为在dt时间内电机总的散热量，J；τ为定子绕组的温升；S为电机的散热面积；a为散热系数。

该方程可以用来描述电机在恒定负载、变负载和断续工作情况下的温升过程。

根据公式（1）得出求解温升的方程，如公式（2）所示。

式中：τW为定子绕组稳定温升，τW=P/aS；τ0为定子绕组初始温升；T为电机的热时间常数，T=cG/aS；t为温升时间。

过载保护元件应该在小于电机温升允许值的情况下，设置阈值动作以及断开电源。求解电机允许温升的方程，如公式（3）所示。

式中：τm为电机的允许温升；tm为稳定温升的动作时间。

当τ0=0时，求解电机的允许温升和稳定温升的动作时间的方程，如公式（4）、公式（5）所示。

式中：τW为电机的稳定温升。

电机损耗P主要由绕组线圈损耗Pr、铁心涡流与磁滞损耗Pm组成。一方面，硅钢片铁损Pm取决磁场强度H，Pm与H2成正比，而磁场强度H与电流I成正比；另一方面，绕组线圈损耗Pr与I2成正比。推算可知，铁心的涡流和磁滞损耗Pm与I2成正比。因此，电机总损耗P与I2成正比。根据能量守恒定律可知，当电流一定时，电机的稳定温升τW与损耗P成正比关系。因此，电机的稳定温升τW与I2成正比。同理，电机允许温升τm与I2成正比。

电机的稳定温升τW与I2成正比就是电流热等效原理。根据该原理可以建立电机热保护积分放大电路的模型。

2 构造电机热过载热学模型

电机产生的热量主要来源于电流流过电机定和转子绕组时所产生的能量。因此，把电机的热源、热熔和热阻分别等效为电流源、成电容和电阻，进而得到电机运行阶段等效热模型，如图1所示。

启动电机，把转子看做堵转，在短暂时间内，可以假设电机没有对周围冷却介质传递热量，即没有散热。该阶段，散热电阻R所在回路处于开路状态。

设定1个计算过热载跳闸阈值的方程，如公式（6）所示。

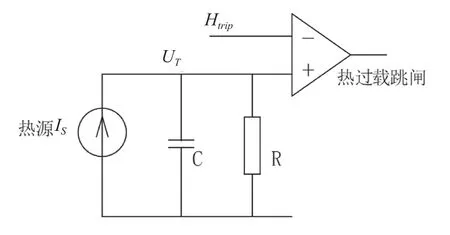
图1 电动机等效热模型

式中：HTrip为过热载跳闸阈值；IL为电机堵转电流；TA为电机启动时间。

电机启动阶段等效热模型，如图2所示。

图2 电机启动阶段等效热模型

图2中，热源的求解方程如公式（7）所示。

式中：Is为等效热源；I1为正序电流；I2为负序电流；K1为正序电流系数；K2为负序电流系数。

由K1和K2的方程（如公式（8）、公式（9）所示）可以求解正、负序电阻的值，如公式（10）、公式（11）所示。

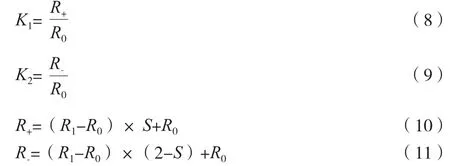
式中：R+为正序电阻；R-为负序电阻；S为转差率；R0为转差率S=0时的正序转子电阻；R1为转差率S=1时的负序转子电阻。

启动过程中，当电机转差率S=1时，就有，就可以把等效热容设定为常数。在SEL749M热保护应用中，设定等效热容常数C=3，那么计算热源的方程如公式（12）所示。

热源IS即电机热功率Pm。分析热积累的过程，在电机启动等效热模型中，电流i在数值上等于热功率Pm，即等于热源IS，由计算电容电流的方程（如公式（13）所示），可以推导出新的方程，如公式（14）所示。

式中：i为电流；du为积分放大电路电压；dt为积分时间。

根据公式（14）可以推导出求解du的方程，如公式（15）所示。

根据公式（15）可以得到关于电压的微分通解方程，如公式（16）所示。

式中：U为电压；t为热保护动作时间；I2为测量电流的平方（包括正序和负序）；C1为常数。

电压U等效于热源经过一段时间热功率而形成的热积累[2]。由该方程可知，t和I2成反比。该方程描述电机启动的过程，假设只有增加热量、没有散失热量且转差率S=1，那么，同轴电机风冷的散热可以忽略不计。上述积分放大电路可以有效分析电机启动过程中的热状态。

3 选择模拟热保护曲线

在热保护积分放大电路模型通解中，t和I2成反比，因此，从IEC非电机专用的中压微机继电保护装置反时限曲线中，筛选出IEC极端反时限曲线C3，模拟电机启动模式的热保护过程。考虑到SEL749M公开了热保护曲线启动模式和运行模式的数值，因此，电机专用保护装置参考标准选用SEL749M过流热保护曲线，见表1。

当计算出热过载额定电流倍数（如公式（17）所示）时，就可以解出IEC极端反时限曲线C3的方程，如公式（18）所示。

式中：M为热过载额定电流倍数；I为测量电流；Ie为额定电流；TD为时间常数，s；tp为保护动作的时间，s。

tp的取值范围为0.4～0.7倍的电机启动时间。在6倍12.5 s的条件下，IEC C3时间常数TD=5.468 s，SEL749M热保护曲线取C5，如图3所示。

在6倍5 s的条件下，IEC C3时间常数TD=2.19 s，SEL749M热保护曲线取C2，如图4所示。

在6倍2.5 s条件下，IEC C3时间常数TD=1.0938 s，SEL749M热保护曲线取C1，如图5所示。

上述分析中将IEC C3极端反时限与SEL749M热保护曲线标准进行对比，取5～12倍的热过载电流动作时间的差值均在0.1 s以内，IEC C3曲线的拟合效果较好。因此，选用IEC C3极端反时限曲线模拟电机在2.5倍以上的热保护模式。

4 IEC模拟热保护反时限曲线的局限性

4.1 保护模式局限性

SEL749M和ABB REM615等电机专用微机保护装置，在运行模式和启动模式中都可以设定电机热过载保护。该文电机启动状态模型是建立在设定启动状态下转差率为1的前提下，而运行状态下转差率近似为0，正序、负序热系数等都需要重新计算，积分放大电路模型也需要重建。因此该文启动模式的数学模型所采用的IEC替代方法，不能向2.5倍以下的运行阶段推广。IEC C3极端反时限曲线只适用2.5倍以上的过电流范围，即启动模式。如果曲线向运行模式延伸，偏差会逐渐增大。因为在2.5倍以下运行阶段的热保护，要更准确地反映热状态、实现全范围的热保护，所以，应该借助其他辅助措施（包括定子测温电阻等）。

表1 SEL749M电机热保护曲线

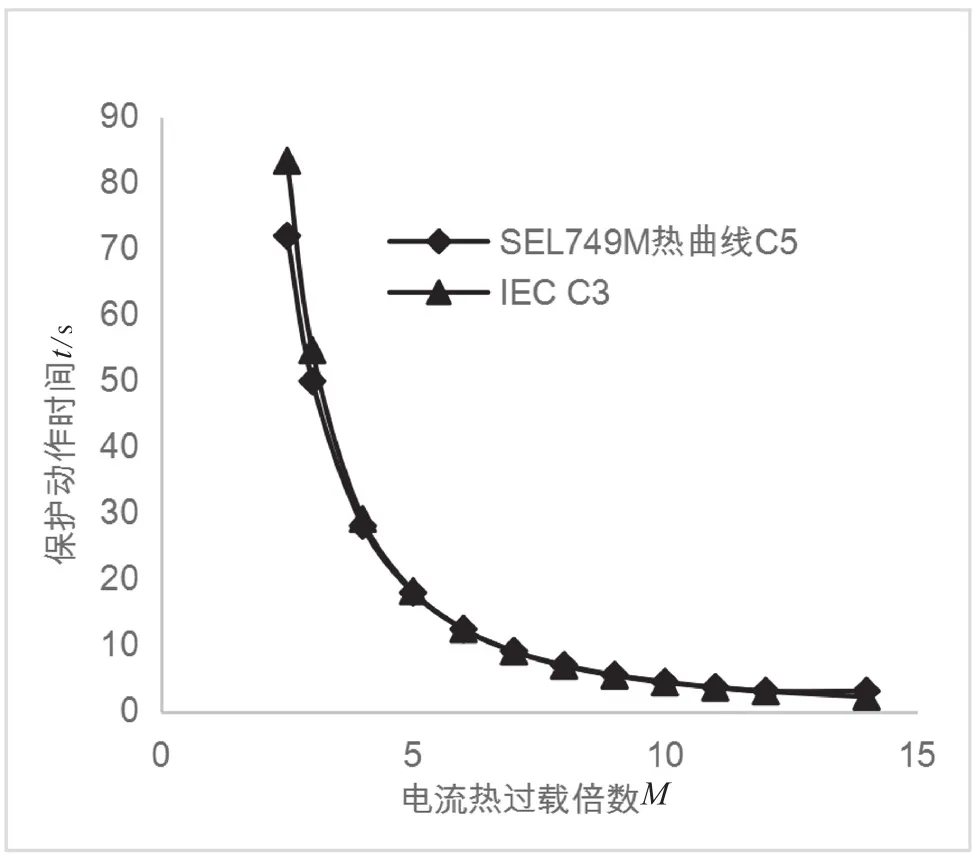
图3 IEC C3对比SEL749M热曲线C5

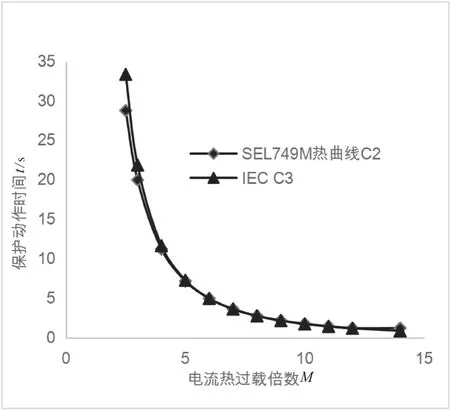
图4 IEC C3对比SEL749M热曲线C2

图5 IEC C3对比SEL749M热曲线C1

4.2 启动时间限制

热保护动作时间是电机实际最大启动时间的0.4～0.7倍。电机专用热保护，可以实现电机动作时间从6倍2.5 s～112.5 s的全范围保护。非电机专用微机保护装置的IEC C3时间常数TD通常较小，对应的电机启动时间也较小，例如，在P123综保中IEC C3曲线取6倍热过载电流，时间常数最大取值可以达到1.2 s，动作时间2.86 s，对应电机启动时间2.85 s～7.14 s；在SEL551中，时间常数最大取值为1.0 s，动作时间2.28 s，对应电机启动时间3.26 s～5.7 s。

电机热保护最理想的解决方案仍然是选用具有热过载保护功能的电机专用微机保护装置，例如SEL749M、REM615等。IEC曲线是根据现有保护装置技术条件采取的替代方案，可用于SEL551、阿海珐P123等非电机专用微机保护装置。

5 应用

冬奥会氢气压缩机项目C201A/B/C机组系统的主体是由氢气隔膜压缩机和驱动机构成。氢气隔膜压缩机型号为MD10-D-800/19-220，轴功率为127 kW，转速为370 rpm，隔膜压缩机转动惯量为362.5 kg·m2；该压缩机采用联轴器直连的传动方式，驱动机电机型号为YBXKK630-16，电压为10 kV，功率为160 kW，功率因数为0.63，转速为370 rpm，额定电流为16.7 A，效率为91.3%，接线方式为Y，电机转动惯量为80.56 kg·m2；电机堵转转矩为0.7倍额定转矩，堵转电流为6倍额定电流，传动机构静阻转矩为0.08倍额定转矩。电机启动方式为全压启动。电机保护装置为阿海珐P127，属于非电机专用中压综保。

5.1 计算电机带载启动时间

电机启动容量的计算，如公式（19）所示。

计算启动回路的额定输入容量时，可以忽略电机电缆的影响，启动回路容量的计算，如公式（20）所示。

式中：Sst为启动回路容量；XL为电缆阻抗；Um为电机机端电压。

已知10 kV母线最大方式下的阻抗X*S1max=9.4046

计算10 kV母线短路容量，如公式（21）所示。

式中：Sk1s1为母线短路容量；Sj为基准容量；为10 kV母线下的阻抗。

当功率因数取0.9时，计算预接无功负荷，如公式（22）所示。

式中：Qfh为预接无功负荷；Sfh为母线短路容量。

全压启动时，计算母线电压相对值，如公式（23）所示。

式中：UstM为母线电压降相对值。

当电机启动时，计算端子电压相对值，如公式（24）所示。

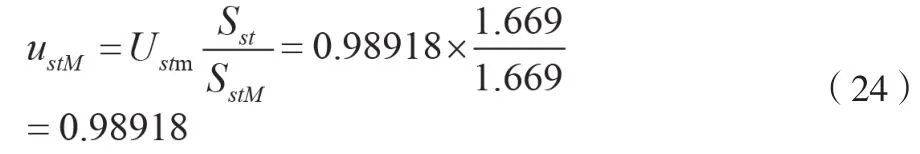
式中：ustM为电机端电压降相对值。

计算tst的方程，如公式（25）所示。

式中：Pe为电机额定功率，Pe=160 kW；GD2为机组总飞轮力矩，设备和电机转动惯量和，即 4×（362.5kg·m2+80.56kg·m2）；ne为电机额定转速，ne=370 rpm；ustM为电机定子端电压相对值，ustM≈0.99；Tst*为电机平均启动转矩相对值，Tst*=0.7；Tj*为电机转动机械静阻转矩相对值，Tj*=0.08；tst为电机带载启动时间。计算电机带载启动时间tst[3]为 6.854 s。