真空管路内压力波动的建模与试验

2020-02-22朱冬詹长书

科技创新导报 2020年28期

关键词：模型

朱冬詹长书

摘要：以真空系统中与真空压力传感器连接的气管为研究对象，建立了管路的二维轴对称模型，提出适当的边界条件，利用有限体积法仿真得到了压力波动结果，与相同参数条件的试验结果较为一致，验证了模型的正确性。真空管路中压力波动是短暂的，但峰值大于大气压，会对压力传感器造成冲击。本文提出的建模方法为进一步研究真空系统的压力波动提供了技术参考。

关键词：真空系统压力波动气动管路模型

中图分类号：TH138 文献标识码：A 文章编号：1674-098X（2020）10（a）-0094-04

Abstract： A two-dimensional axisymmetric model of the gas pipe connected with the vacuum pressure sensor in the vacuum system is established， and the appropriate boundary conditions are proposed. The pressure fluctuation results are simulated by using the finite volume method， which are consistent with the test results under the same parameter conditions， and the correctness of the model is verified. The pressure fluctuation in vacuum pipeline is transient， but the peak value is larger than atmospheric pressure， which will impact the pressure sensor. The modeling method proposed in this paper provides a technical reference for further study of pressure fluctuation in vacuum system.

Key Words： Vacuum system; Pressure fluctuation; Pneumatic pipeline; Model

真空系統广泛应用在电子半导体组装、汽车生产线、食品[1-2]加工等多个行业，用于搬运芯片、汽车玻璃等易损易碎物件。通过真空发生元件（真空泵或真空发生器）产生真空，使系统内部压力低于大气压[3-4]，在吸盘内外表面产生压力差使其吸附于工件表面，以便对工件进行操作[5]。

操作结束后，真空系统与大气环境接通，系统内部压力迅速升高至大气压，真空条件被破坏，吸附力消失，吸盘与工件脱开。与真空压力传感器连通的管路内压力也迅速回升，并在气管中产生压力波动。压力波动会对压力传感器造成冲击，多次冲击可影响传感器准确性和使用寿命，对真空系统的安全性和可靠性带来隐患。许多学者对气动系统中的压力波动进行了研究。仇艳凯等[6]设计了一种液压消声器，分析了其吸收压力波动的效果。刘威志[7]对管路内气液两相流中压力波动特性进行了分析，根据不同位置的波动特性对流动形态进行了划分。

以上研究多集中在正压系统或两相流中的压力波动，本文以真空系统中与真空传感器连接的管路为研究对象，通过仿真和试验对其中的压力波动进行研究，探寻压力波动的规律。

1 模型的建立

真空系统一般由真空发生元件、真空减压阀、气管、控制阀、真空压力传感器和吸盘等组成。本文研究重点是与压力传感器连接的管路内的压力波动，因此以一端与压力传感器连接、另一端与真空系统连接的管路为研究对象，建立二维轴对称模型，如图1所示。为了流场计算的准确性，在模型中加入了大气区域（或真空区域）。

在本文的研究中设定：

（1）系统中气体为理想气体;

（2）忽略重力的影响。

管路中气体流动遵循质量守恒定律、动量守恒定律和能量守恒定律等。控制方程如下：

（1）连续性方程。

（2）轴向和径向的动量守恒方程。

（3）能量守恒方程。

（4）状态方程。

2 边界条件及初始条件

真空系统一个完整的工作过程包括抽真空、真空维持、压力回复和常压等4个阶段。

抽真空阶段时，图1中区域2为大气压，区域4为真空，1为管路出口，气体从管路中抽出使管路中压力降低至设定真空值。真空维持阶段时，系统内部压力为某一真空值，吸盘处于吸附工件状态，此时图2中区域2和区域4均为真空状态。

压力回复阶段时，图1中区域2为真空，区域4为大气压，1为管路入口，气体向管路充气使管路内压力迅速回升至大气压。常压阶段时，系统内部压力为大气压，吸盘和工件脱开，处于不工作状态，此时图1中区域2和区域4的压力均为大气压。

初始时管路中为真空压力，先向管路中充气使气体压力回复至大气压并进入常压阶段，然后将管内压力抽至真空状态并维持真空。

3 数值结果及试验验证

为了验证本方法的正确性，现给出一算例，主要参数为：管路长度1000mm，管路内径4mm，真空压力为10kPa（绝对压力，下同），大气压为100kPa，压力回复时间和抽真空时间均为1s。气体温度为300K。

3.1 管路中监测点的设定

分别在管路中设置3个监测点，如图2所示，分别为位于管路与真空压力传感器的连接处即管路末端的A点、位于管路中间的B点和位于管路入口处的C点。

3.2 试验系统的建立

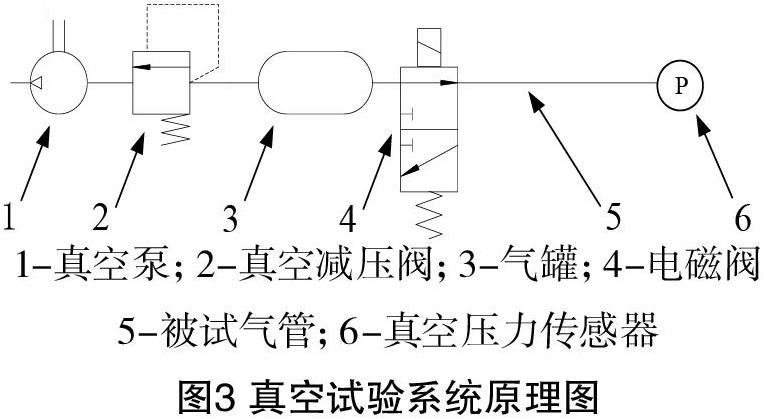
建立真空试验系统，气动回路如图3所示。通过真空泵抽取系统内空气，利用真空减压阀调整系统的真空压力。气罐用于稳定管路中的真空压力。通过计时器控制电磁阀的通断电，使被试气管按设定时间与大气环境及真空系统联通，实现气管中大气压和真空压的更替。

真空泵为旋片式泵，抽速为9L/s。真空减压阀的最低设定压力为5kPa。气罐容积为5L，电磁阀为二位三通阀，实现被试管路压力在真空和大气压之间切换。管路长度1000mm，管路内径4mm，材质为聚氨酯。

3.3 数值结果分析

通过数值仿真得到管路末端A点的压力值，相同条件下试验测量的管路末端压力如图4所示。

图4表明，管路内气体依次经历了压力回复、常压、抽真空和真空维持等阶段。图4（b）为局部放大的A点压力曲线，仿真结果表明A点的第一个波峰出现在0.008s，最高可达125.5kPa;第一个压力波谷出现在0.014s，最低可达88.4kPa，压力波动经历了5次振荡，历经约0.07s。通过试验测得的A点第一个波峰出现在0.024s，其值为107.8kPa，第一个波谷出现在0.038s，压力为92.8kPa，压力波动经历了5次振荡，历经约0.14s。与仿真结果相比，试验得到的压力波动峰值要低于仿真结果，且波峰出现的时刻也晚于仿真曲线。这是因为仿真计算时管路壁面为固体材质，不具有弹性，试验用气管为聚氨酯材质，具有一定的弹性。当管内压力高于大气压时，气管在径向方向会有一定的膨胀，在此过程中会吸收气体的部分压力能，降低了压力波的峰值，并延后压力波的出现。从整体上看，试验压力与仿真得到的压力曲线是一致的，表明所建立模型和采用的计算方法是可行的。压力波动仅在压力回复阶段出现，整个过程很短暂，随着时间的推移逐渐衰减并维持在大气压。

初始时，管路内压力为真空压10kPa，管路入口气体压力为100kPa，在压差作用下气体以一定初速度向气管充气。当气体到达气管末端即气管与压力传感器连接处时，紧靠压力傳感器的流体首先停止流动，相邻的流体依次停止流动，最终管路入口处流体也停止流动。在各处流体依次停止流动的同时，流动的动能转化为压力能，致使已停止流动的气体产生压力升高的现象，这是压力峰值出现的原因。

图5为仿真得到的管路末端（A点）、中点（B点）和入口（C点）的压力曲线。由图5可以得到，由于B点的速度小于A点的速度，所以B点的第一个压力波峰小于A点的压力波峰值。管路入口C点和大气区域连通，大气区域的压力恒为大气压，因此C点压力几乎无升高和波动。

管路内气体压力的第一个波峰值高于大气压，在压差作用下，气体向大气区域反向流动，使气体离开管路，导致管路中的压力在达到波峰值后开始降低，最低可至大气压以下，从而出现压力波谷。图5中B点的第一个压力波谷高于A点的压力波谷值。

当管路内压力均达到波谷值，压力低于大气压，气体再次向管中充气，重复上述过程。由于波谷值高于初始压力10kPa，因此压力的第二波峰低于第一个波峰值，波谷值高于第一个波谷值。随着时间的推移，管路内压力波动逐渐消失，最终稳定在大气压。

4 结语

本文研究了与真空压力传感器连接的气管中的压力波动，建立了仿真模型并进行了计算，得到了以下结论：

（1）仿真结果与试验结果的一致性较好，表明所采用的二维轴对称模型和方法是可行的;

（2）管路中的压力波动存在于从真空向大气压回复的阶段，整个过程很短暂，但压力峰值可达125.5kPa，会对真空压力传感器造成一定的冲击;

（3）管路的膨胀性可降低压力波动的峰值，延迟压力波动的出现，对压力波动有一定的抑制作用。

参考文献

[1] 聂俊峰，王涛，许英南，等.柔性吸盘真空系统性能试验[J].液压与气动，2020（5）：131-137.

[2] 赵汉雨，黄伟华，刘存祥.禽蛋卸托机气动系统的设计[J].液压与气动，2016（4）：97-100.

[3] 李勇，郭喜龙.真空发生器混合室直径参数的研究[J].机械制造，2019，59（7）：42-46.