线性需求下铁路客运差别定价模型研究
2020-02-22朱颖婷单杏花
朱颖婷,单杏花
(中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081)
我国铁路客运旅客群体庞大,客流表现出明显的季节性特征,往往在节假日等客运高峰期出现一票难求的现象,而在淡季时部分列车可能出现席位闲置的现象。在出发时间上,旅客也更喜欢选择白天出发、白天到达的车次出行,一些开车时间在清晨或到达时间在深夜和凌晨的车次,客座率往往较低,客运淡季时尤为明显。列车席位资源利用率不均,在一定程度上影响了铁路运营部门的收益,降低了旅客出行的舒适度和便捷性。
不少学者将上述问题归结于我国铁路客运票价制度,认为调整票价策略可以改善铁路旅客出行体验,并提高铁路运营部门的收益。票价调整的一个重要策略是差别定价,差别定价是指销售商在销售完全相同的产品或者有细微差别的同一产品不同款式时,对不同顾客制定不同价格的行为。它根据客户选择行为或者产品特征做市场细分[1],对高支付意愿的顾客收取高价,对低支付意愿的顾客收取低价[2]。航空、酒店等行业通常根据用户对企业的贡献不同,将用户划分成不同用户群,对不同用户群采用不同的价格,以培养稳定的用户群,从而获取额外利润[3-5]。文献[6]和[7]分别采用动态规划Bell-man最优化原理和最大凹向包络定理研究了我国铁路客运最优票价策略;文献[8]从季节和列车开行区域2方面分析了我国铁路客运采用差别定价的可行性;文献[9]~[13]讨论了对我国铁路客运做市场细分、进行差别定价的可行性。但是上述文献仅仅论证了对我国铁路客运进行差别定价的意义,均未对差别定价模型作量化研究分析。
国外针对铁路客运的票价策略研究较为实用。在应用上,日本、德国等国家针对不同用户采用灵活的动态票价折扣策略[14]。在理论研究上,Ngostino依据旅客出行可能考虑的各种因素(如列车开点、到达时间、出行距离)建立了消费者行为选择模型,以此来确定铁路客运票价策略[15];Sidbari等人将时间以天为单位离散化,介绍了4种动态铁路客运票价策略:动态规划模型,短期策略,静态票价启发式策略,随机动态启发式策略[16];Bharill根据印度铁路公司一趟快速列车的3种席别在9周内的订票数据,分析票价和需求间的关系,预测未来的订票需求量及退票数,最终达到提高收益的目的[17]。
本文为提高席位资源利用率,以收益最大化为目标,研究了我国城际铁路(只途经2个车站)在客运淡季时的差别定价模型,确定旅客群的最优细分数目,以及每个旅客群的最优票价。
1 基于完全价格歧视策略的收益分析
1.1 模型假设
本文的模型基于以下假设:
(1)当旅客认为其得到的消费者剩余最大时,才购买相应时段的车票出行;
(2)每位旅客每次只能购买一张车票,旅客的购票需求为其最大支付意愿与票价的线性函数,且最大支付意愿服从均匀分布;
(3)在规定时间段内,不考虑旅客需求转移的情况,如高支付意愿旅客购买低价车票等。
1.2 模型概述
令最大支付意愿w∈[0,b],且w服从均匀分布,旅客购买价格为p的车票的需求概率为q(w,p)=max{0,(w–p)},从而每位旅客为铁路运营部门带来的期望收益r(w,p)为:
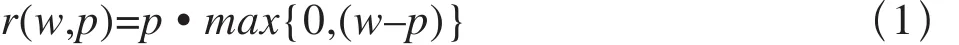
根据经济学中对完全价格歧视的定义,若垄断者能够使相同产品对不同用户采用不同的价格策略,就能够获取所有用户的消费者剩余,从而获得最大收益。若不考虑黄牛倒卖车票、旅客退票改签等行为,根据式(1)可知,当p=w/2时,r(w,p)取得最大值w2/4,当在铁路客运淡季运能充足时,能够完全满足旅客购票需求,则最大收益为:

但完全价格歧视是一种极端情况,铁路客运运营部门需要知道每一位旅客的最大支付意愿,以此确定各时间段列车票价,这在现实中是不可能的。因此,可采用市场细分的策略,对不同子市场制定不同的票价,以此调整铁路客流,将支付意愿较低的旅客吸引至客流闲时乘车出行,在提高铁路客运资源利用率的基础上,增加铁路运营部门的收益,提升旅客出行的舒适度。
2 线性需求下铁路客运差别定价模型
2.1 模型定义
假设某城际铁路客运起止点(OD,Original–Destination)在一段时间内的所有旅客Ak可以被划分成k个子市场,Ak={A1,A2,…,Ak},旅客只能在经过该OD的n趟车中选择某1趟车出行,则1 ≤k≤n,子市场Ai对应票价为Pi(i=1,2,…,k),票价集合Pk={P1,P2,…,Pk},对应的可售出席位数为Ck={C1,C2,…,Ck}。在某一段时期内,所有旅客能够被细分,即每位旅客仅属于一个子市场Ai,在购票时只能按照唯一票价Pi购票。若最大支付意愿为xim和xin(xim<xin)的两名旅客均属于子市场Ai,那么当旅客a的最大支付意愿xi∈[xim,xin]时,旅客a也属于子市场Ai。旅客的最大支付意愿xi服从均匀分布,最大支付意愿集合Xk={0,x1,…,xi,xi+1,…,xk–1,b},且 0<x1<…<xi<xi+1<…<xk–1<b,则各子市场定义为:

从旅客的角度分析,旅客出行时票价必定满足如下2个条件:

最大支付意愿越小的旅客出行时所能接受的票价越小,且当票价小于最大支付意愿,即旅客的消费者剩余大于0时,旅客才会选择乘车出行。
根据上述分析,得到子市场Ai的累计购票需求为:
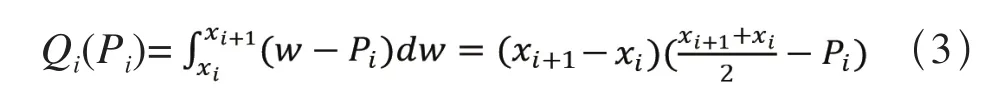
Ai的收益为:

总收益R(k)为:

以收益最大化为目标,得到本文提出的铁路客运差别定价策略优化模型为:

其中,0<P1<…<Pi<Pi+1<…<Pk<b;Pi≤xi(i=1,…,k);xk+1=b;且Qi(Pi)≤Ci。
2.2 最优差别定价分析
可证明目标函数R(k)为凹函数,下面重点分析淡季时最优票价和市场细分数应该满足的条件。
(1)在客运淡季,旅客购票需求明显小于可售席位数,即无论如何细分及调整价格,都满足Qi(Pi)≤Ci的约束,上述最优化问题可被看作无约束最优化问题,为了便于计算,令b=1,根据无约束优化的一阶条件可知:

显然,Pi+1–Pi>0,xi+1–xi>0,根据式(7)和式(8)可得到:


(2)市场细分数目k越大,旅客群的划分越平滑,将最优解xi*和Pi*代入式(1),得到总收益为:

可证明R*(k)是关于市场细分数目k的凹函数。从经济学角度看,随着k无限增大(k→∞),票价策略逐渐趋于完全价格歧视,铁路运营部门可以获得每个旅客的全部消费剩余,进而获得最大收益R*。但完全价格歧视是一种极端现象,现实中很少发生。由于铁路客运用户群庞大,铁路运营部门不可能对每一位旅客制定完全有差别的票价,且铁路部门在我国还承担着社会公益性角色,不可能采取完全价格歧视的定价策略。我们观察k值增大时,R*(k)及其与R*比值的变化规律,如表1所示。

表1 R* (k)关于k值的变化规律列表
从表1可以看出,当k=1时,代表采用固定票价的策略,此时收益最小,仅为完全价格歧视下收益的88.9%;当k=3时,R*(k)/R*达到98%;当k=5时,R*(k)/R*已经达到99.2%;随着k继续增大,R*(k)/R*增大的速率降低,R*(k)/R*趋于100%。
因此,客运淡季时市场细分数目和旅客人数多少无关。进行差别定价时,从实际应用的易操作性看,将旅客划分为3~5个子用户群即可。根据式(9)和式(10)可以得到市场细分的最优支付意愿划分范围,以及各个子用户群相应的票价。在淡季时采用差别定价策略更容易估计其期望收益,降低了实施差别策略的风险性。
3 结束语
本文假设旅客需求和最大支付意愿为线性关系,研究了城际列车淡季时的差别定价模型,该模型可同时求解最优票价等级个数及各级最优票价,对铁路运营部门实行差别票价策略具有一定的理论指导意义。其中的难点在于分析旅客的最大支付意愿分布,以及旅客需求在何种情况下发生转移,这需要开展大量科学、合理的铁路旅客出行需求调查,分析旅客出行需求偏好,从而进一步优化铁路客运差别票价模型。
