一种负刚度动力吸振器的数值参数优化

邢昭阳, 申永军, 邢海军

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

动力吸振器(dynamic vibration absorber, DVA)作为一种抑制系统振动的设备已经广泛应用于工程领域。自Frahm[1]发明第一个DVA以来，很多学者便以提高DVA的减振效果为目标对DVA的结构进行了改进与优化，形成了3种传统的模型：Voigt型DVA[2]、接地型DVA[3]和三要素型DVA[4]，在实际工程中可以根据不同的使用条件和要求选择合适的模型。目前，由Den Hartog[5]和Ormondroyd[2]提出的固定点理论被广泛应用于DVA的参数优化，成为国内外认可的经典理论。由于通过固定点理论求得的DVA的最优参数并非是精确解，Nishihara和Asami[6-8]推导得到了DVA的级数解，发现与固定点理论推导的结果非常接近。经典的DVA虽然能够有效减小主系统振动，但只对高频振动效果明显，当主系统受到低频激扰时，它们的减振效果会明显变差。近些年来，学者们发现负刚度元件能够提高振动控制系统的控制性能。负刚度的概念由Molynewx[9]首次提出。为了提高振动控制的性能，Alabuzhev et al[10]提出在隔振系统中使用负刚度装置。Lakes et al[11]研究发现负刚度元件本身是不稳定的，需要与正刚度元件并联使用才能发挥作用。彭献等[12-13]从能量角度分析了正、负刚度并联系统的工作原理，并且提出了基于正、负刚度并联使用的准零刚度隔振器的设计方法。彭解华等[14]强调了正、负刚度元件并联使用的稳定性问题，从能量角度推导了弹性系统静态稳定性的刚度准则。彭海波等[15-17]基于负刚度元件的稳定性提出预加荷载使主系统产生的最大位移不大于固定点处响应值时，系统将处于稳定状态，研究发现在3种经典的DVA模型中加入接地负刚度元件能够提高DVA的减振效果。

序列二次规划算法收敛性好、计算效率高，是一种求解约束非线性优化问题的有效方法[18-20]。Matlab 作为目前科学与工程计算的主流软件，其优化工具箱中有许多优化函数，其中fminimax函数基于序列二次规划法可以用来求解最大值最小化问题。由于在动力吸振系统中，主系统的幅频曲线存在2个峰值，H∞优化的最终目的是为了让这2个峰值等高且尽可能地降低，本质上是最大值最小化问题，可以应用fminimax函数对DVA进行优化设计。本文提出了一种含有负刚度元件的动力吸振器模型，由于推导公式比较复杂，首先利用Matlab优化工具箱编写了优化程序，验证了程序的有效性与正确性，然后对所提出的模型进行了数值参数优化设计，得到了该模型的局部最优参数，与其他模型对比发现本文模型具有良好的减振性能。

图1 动力吸振器模型

1 动力吸振器模型

图1所示为本文提出的含有负刚度元件的动力吸振器模型，其中，m1为主系统质量；m2为吸振器质量；k1为主系统刚度；k2为吸振器刚度；k3为接地负刚度元件的刚度；c2为阻尼器的阻尼；x1、x2分别为主系统的位移和动力吸振器的位移，主系统与接地负刚度元件同时受到振幅为x0、频率为ω的简谐位移激励。

根据牛顿第二定律可以得到该系统的动力学微分方程为

(1)

(2)

设解的形式为x1=X1ejωt,x2=X2ejωt并代入式(2)得到

X1=[x0(jA1+B1)]/(jC1+D1)

(3)

进一步求得主系统的振幅放大因子

(4)

式中,A2=2βλ(1+nμβ2)；B2=(1+n)β2-λ2+nμβ4；C2=2βλ[1+nμβ2-λ2(1+μ)]；D2=(1+n)β2+λ4+nμβ4-λ2[1+β2(1+n+μ)]。

图2 在不同阻尼比下的归一化幅频曲线

由固定点理论易证归一化的幅频曲线均通过2个独立于阻尼比的点，也就是该模型主系统幅频曲线的固定点。图2中给出了阻尼比分别为0.2、0.4和0.6时的归一化幅频曲线，从图中可以看出对于不同的阻尼比，曲线均通过P、Q两点。从理论角度看，该模型可以运用固定点理论进行参数优化设计，但是负刚度项的存在使得解析公式较为复杂，于是尝试用数值优化方法对系统参数进行优化设计。

2 动力吸振器的数值优化方法

2.1 数值优化方法的Matlab实现

对于一般的DVA来说，系统的频率比与阻尼比的数值分别为在区间[0,2]与[0,1]内，于是DVA的H∞优化数学模型可以表示为

(5)

式中，β和ξ分别为系统的频率比和阻尼比；A是以频率比和阻尼比作为变量的函数。

Matlab优化工具箱中自带的fminimax函数可以直接调用，不需要进行复杂的程序编写，其使用方法为[21]:[x,fval,maxfval]=fminimax(@fun,x0,a,b,Aeq,Beq,lb,ub)，其中，x为最优化的目标函数值对应的自变量，fval为目标函数值，maxfval为目标函数的最大值，fun为目标函数，x0为自变量的初值(可以用随机数产生)，a、b为线性不等式约束ax≤b,Aeq、Beq为线性等式约束，lb、ub为自变量的下界与上界。

图3 局部最优解和全局最优解

在使用该函数时有一些需要注意的问题：该函数对自变量的初值x0的选取比较敏感，选择不同的初值可能会得到不同的结果，因此为了使数据真实有效，对文中出现的每个模型均使用随机数作为自变量的初值并运行了100次。为了得到有意义的系统参数，尽管把系统的频率比与阻尼比的取值范围设为[0,2]与[0,1]，有时可能会在此区间内得到局部最优解和全局最优解，如图3所示，其中M处为局部最优解，N处为全局最优解，这时能够使主系统位移的时间历程曲线收敛的解才是DVA的最优参数。

2.2 数值优化方法的验证

为了验证数值优化方法的正确性，使用该方法对图4所示的Voigt模型以及图5所示的含有负刚度元件的Voigt模型进行了研究。

图4 Voigt型动力吸振器

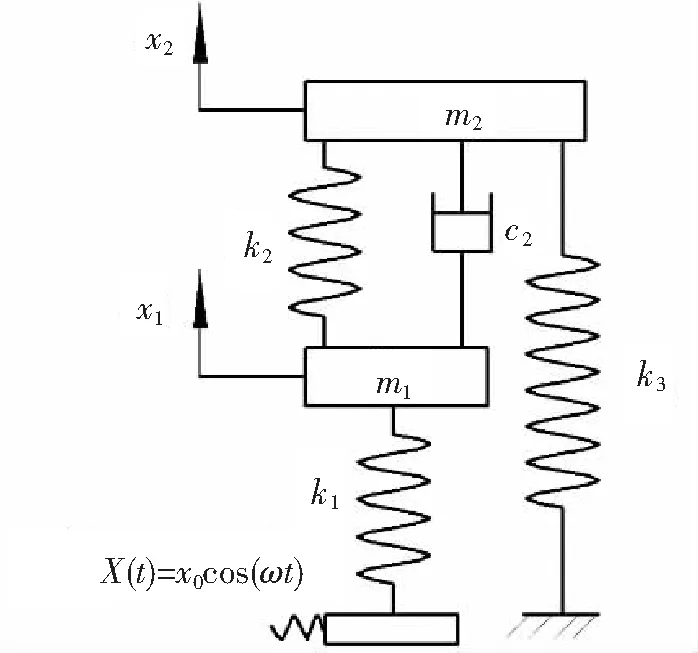
图5 含负刚度元件的Voigt模型

2.2.1 Voigt型DVA的数值优化

表1 Voigt模型的最优参数

图6 Voigt型DVA主系统归一化的幅频曲线

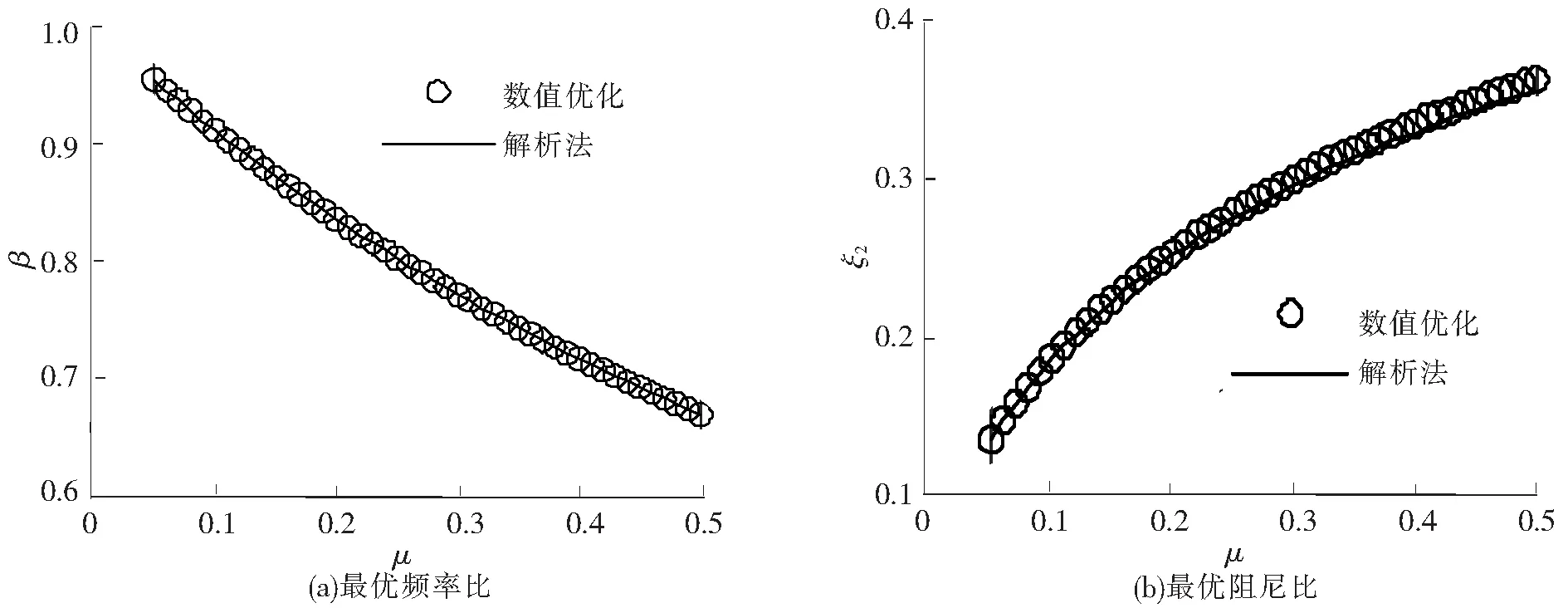
图7 最优参数随质量比的变化曲线

从图6中可以看出，由数值优化方法和解析法得到的主系统幅频曲线几乎完全重合，图7中由2种方法得到的最优频率比曲线完全吻合，而最优阻尼比的曲线稍有偏离，其原因已在上文给出，属于正常现象。据此判断该数值优化方法适用于Voigt型DVA。

2.2.2 含负刚度的Voigt模型的数值优化

图5所示的含负刚度元件的Voigt模型，其主系统受到振幅为x0、频率为ω的简谐位移激励，彭海波等[15]研究了该模型主系统受到振幅为F0、频率为ω的简谐力激励时的减振效果。经过简单的推导，发现在受到相同频率的位移激励和力激励的情况下，主系统的振幅放大因子完全相同。利用固定点理论及负刚度理论可以得到解析方法下图5所示模型的最优参数表达式[15]

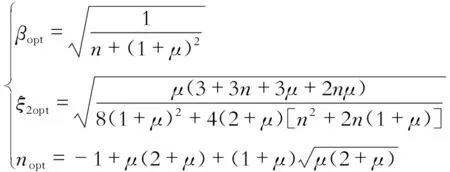
(6)

进一步整理后得到

(7)

下面使用数值优化方法对该模型进行优化，选取质量比μ=0.1，得到了2组频率比、阻尼比和负刚度比的数值解

(8)

(9)

通过观察主系统的位移时间历程曲线是否收敛可以验证2组参数的有效性。使用式(8)和式(9)中得到的优化参数，分别绘制了当λ=1时主系统位移的时间历程曲线如图8(a)和图8(b) 所示，当系统使用式(8)中的参数时，主系统的位移时程曲线才能够收敛，因此这组参数是该模型的最优参数。表2汇总了μ=0.1时解析法和数值优化方法得出的最优参数值及两者之间的偏差，比较各参数发现2种方法得到的最优负刚度比偏差极小，最优频率比的偏差不超过2%，最优阻尼比的偏差较大。结合式(6)可知，由于数值优化方法与解析法得到的最优参数nopt存在微小的偏差，在βopt和ξ2opt中该偏差被放大了。除此之外，与Voigt型DVA的情况相同，在求解ξ2opt时将2个固定点处求得的最优值ξP和ξQ的平均值作为最优参数是最优阻尼比偏差较大的主要原因。

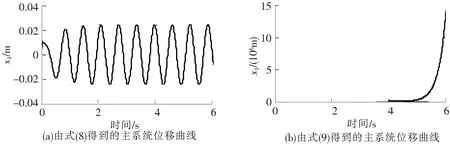
图8 主系统位移时间历程

图9 归一化的主系统幅频响应曲线

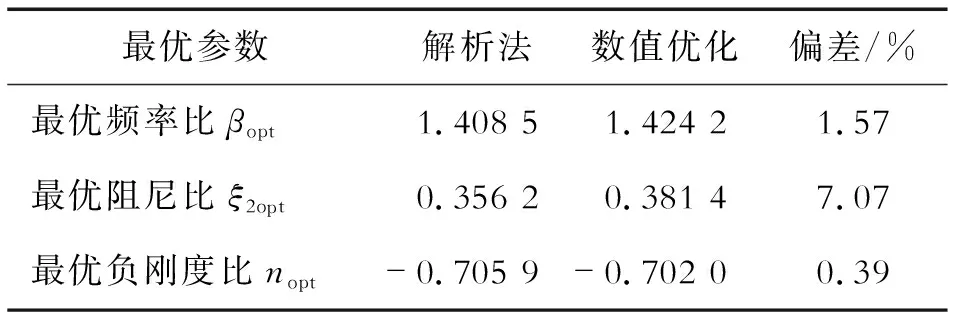
表2 含负刚度元件的Voigt模型的最优参数

为了更直观地比较2种方法的优化效果，在各自最优参数下绘制了主系统归一化的幅频响应曲线如图9所示。从图9中可以看出数值优化达到了与解析法相近的优化效果，实现了共振峰值的完全等高设计，而且数值优化相比于解析法绘制的幅频曲线的峰值要更低，达到了更好的优化效果。

通过上述分析，将基于fminimax函数的数值优化方法应用于DVA的参数优化设计，达到了与解析法相同的优化效果，验证了该数值优化方法在DVA优化设计中的可行性，为动力吸振器的参数优化提供了一种方法。

3 动力吸振器的数值优化

3.1 最优参数的求解及验证

将图1所示模型的频率比β、阻尼比ξ2和负刚度比n作为设计变量，以β、ξ2和n的取值范围作为约束条件，将式(4)中主系统的振幅放大因子作为目标函数，选取质量比μ=0.1，使用数值优化方法对DVA进行了参数优化设计。随机产生初始点x0运行了100次后发现得到了很多组不同的解(由于这些解并不能帮助得到本模型的最优参数，并未在文中列出)，与图3中描述的情况类似，其中还存在一些导致主系统位移时程曲线发散的解。出现该现象的原因是fminimax函数对初值x0比较敏感，对于该模型来说较难找到有意义的最优解，但是发现通过数值优化方法求得的频率比数值几乎都位于区间[1.9,2]，这说明该模型的最优频率比就在此区间内。于是通过减小频率比的上界，试图寻找该系统的局部最优解，当频率比的上界减小到一定值后，无论随机产生的初值x0为何值，经过多次循环后只会得到同一组数据，这组数据便是该系统的局部最优解。每次将上界减小0.1，最终在频率比上界为1.9时得到了100组相同的数据：βopt=1.900，ξ2opt=0.337，nopt=-0.734。将这组参数代入到式(4)，绘制了主系统归一化的幅频曲线，并通过绘制主系统位移时程曲线和四阶荣格库塔法进行了验证，如图10所示，图10(a)中给出了主系统的位移时程曲线；图10(b)中给出了主系统归一化的幅频曲线。

图10 数值优化参数的验证

从图10看出，主系统的位移时程曲线是收敛的，由数值优化方法和四阶荣格库塔法得到的幅频曲线吻合良好，说明数值优化方法求得的最优参数在本系统中是正确且有意义的。尽管通过数值优化方法得到的最优频率精度只有小数点后一位，但是该模型仍然具有优良的减振性能，其最大振幅放大因子数值在1附近，且幅频曲线的第一个共振峰几乎位于λ=0处，说明该系统具有较低的谐振频率。

3.2 与其他模型的对比

图11 随机激励时间历程

在实际工程中大部分激励为随机激励，因此进一步研究了主系统在随机激励下的响应，构建了100 s均值为0、方差为1的随机位移激励，其时间历程如图11所示，主系统不附加DVA的位移响应如图12(a)所示。选取主系统质量为m1=1 kg、质量比μ=0.1、主系统刚度为k1=100 N/m，根据文献[5]、文献[15]和本文得到的最优参数绘制了主系统附加3种不同DVA的位移响应曲线如图12(b)～图12(d)所示。观察图12可以发现，本文模型相比于其他模型具有更优良的减振性能。

图12 主系统时间历程

4 结论

研究了一种含负刚度的低频动力吸振器，由于该模型很难通过解析法进行研究，提出了一种基于动力吸振器H∞优化的数值优化方法，并验证了该方法的正确性，使用数值优化方法对该模型进行了参数优化。研究发现当质量比μ=0.1时，通过数值优化方法得到了系统的最优频率比、最优阻尼比和最优负刚度比分别为：βopt=1.900，ξ2opt=0.337，nopt=-0.734，尽管并没有得到非常精确的系统参数，但是其幅频曲线的第一个共振峰几乎位于λ=0处，且最大振幅放大因子数值在1附近，说明该系统具有较低的谐振频率，在简谐激励与随机激励下与其他模型相比，本文模型能够更大程度地抑制系统振动，表现出了优良的减振性能。进一步研究表明，本文提出的数值优化方法还能够对主系统含阻尼的模型进行参数优化设计，该方法为一些复杂而难以进行解析推导的线性系统提供了一种可行的优化方案。