基于稀疏编码和极限学习机的设备故障诊断方法及应用
2020-02-22邓飞跃强亚文
邓飞跃, 强亚文
(1. 石家庄铁道大学 河北省工程机械动力与传动控制重点实验室,河北 石家庄 050043;2. 石家庄铁道大学 河北省大型工程机械装备制造协同创新中心,河北 石家庄 050043)
0 引言
滚动轴承作为旋转机械中的核心组件,其状况直接影响了机械整体的正常运行。在旋转机械的各类故障中,滚动轴承故障约占30%,对滚动轴承的运行状态进行准确识别,能够及时发现轴承故障以制定维修计划,保证机器的正常运行。同时由于旋转机械运转过程中时刻产生着海量监测数据,给故障诊断带来了诸多挑战,传统的支持向量机(SVM)、BP神经网络等方法由于或多或少存在一些缺陷[1-2],限制了其实际应用。
极限学习机(Extreme Learning Machine,ELM)作为一种新型神经网络学习方法,相比其他神经网络方法拥有更快的学习速度和泛化性能,已成功应用于多个研究领域[3-9]:Cao et al[3]基于ELM和稀疏表示分类算法提出了一种用于图像分类的混合分类器;Zhang et al[4]提出了一种基于极限学习机的去噪自动编码器,并将流形正则化框架引入其中,提高了图像的识别性能;林怡等[5]利用鱼群寻优算法优化极限学习机的正则化参数和核参数,增强了遥感影像分类的准确度。上述研究均取得了较好的结果,证实了ELM方法具有良好的工程应用前景。与此同时,ELM方法在机械设备故障研究中也得到了较好的应用:Li et al[6]提出一种稀疏与邻域保持深层极限学习机算法,成功用于旋转机械的故障诊断;皮骏等[7]基于改进遗传算法优化极限学习机网络,将其应用于滚动轴承故障诊断;郑近德等[8]提出了一种基于极限学习机的变量预测模型用于滚动轴承的劣化状态识别;裘日辉等[9]基于PCA和极限学习机提出了单分类算法,获得了较高的分类准确率。这些方法虽然具有积极的借鉴意义,但由于ELM模型中输入权值和阈值是随机生成的,有可能导致病态问题的出现[10],因此在ELM特征向量输入方面仍需要进行进一步的研究。
基于上述分析,以极限学习机的模型输入为出发点,讨论了一种新型模型输入的极限学习机并应用于故障模式识别。该方法首先通过K-Singular Value Decomposition(K-SVD)方法提取样本数据的自适应字典,基于该字典使用正交匹配追踪(OMP)对样本数据进行稀疏编码,将稀疏编码作为模型输入。通过美国西储大学发布的10类滚动轴承故障数据测试,该方法在多种不同故障类型以及不同故障程度识别中具有较好的诊断正确率和可靠性。
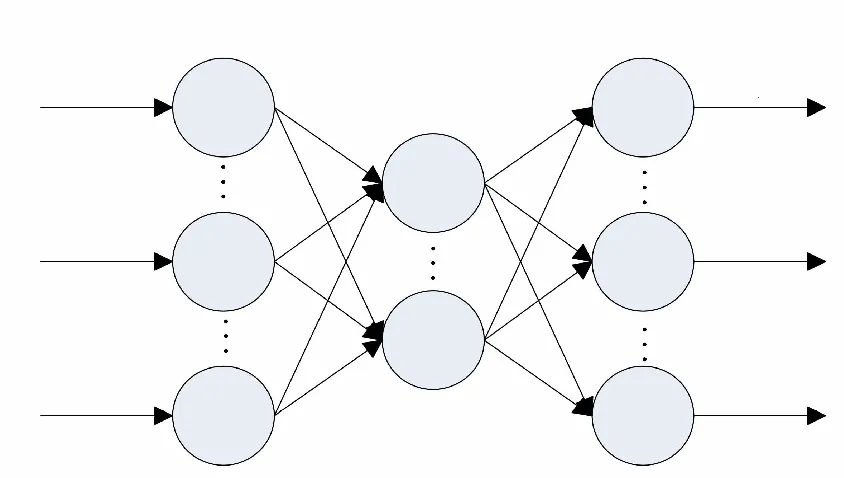
图1 极限学习机结构图
1 极限学习机模型
极限学习机具有和传统单隐层神经网络相同的网络结构[11],但其输出权值矩阵根据最小范数最小二乘解理论一部求解得出,所以具有更快的训练速度。
极限学习机的结构见图1,设有N个训练样本(X,T),X=[x1,x2,…,xN],T=[t1,t2,…,tN],则模型的输出可表示为
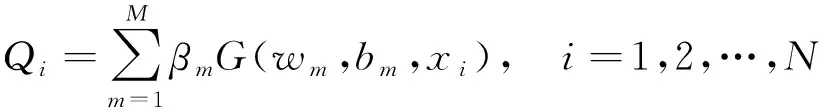
(1)
式中,M为隐藏节点个数;wm、bm分别为随机给定的隐藏节点的输入权重和偏置;βm为输出权重;G为隐含层的激活函数,文献[4]给出了几种常用的激活函数。式(1)还可以改写成如下矩阵形式
O=Hβ
(2)
式中,H=G(wx+b)为隐含层输出矩阵,ELM的训练目标为
‖T-Hβ‖=0
(3)
隐含层的输出权值
β=H+T=(HTH)-1HTT
(4)
式中,H+表示H的Moore-Penrose广义逆。
由此可见,ELM模型免去了传统算法中的参数设置以及迭代计算过程,计算更加简便,极大地提高了网络构建的速度。本文使用ELM分类模型[12]用于故障模式识别。
2 模型输入
实际工程振动信号数量巨大,并且包含大量背景噪声,若直接作为模型输入进行诊断,不仅诊断准确率得不到保障,而且严重降低诊断效率,所以有必要对数据进行消噪与降维处理。
2.1 改进型K-SVD算法
K-SVD字典学习算法以稀疏编码-字典更新的循环迭代方式来对样本信号进行学习,相比传统字典拥有更好的自适应能力,对信号的表示也更稀疏。同时为提高学习速度,采用改进型K-SVD算法[13],其具体过程如下:
(1)给定学习样本Ym×n,设定K-SVD算法参数:迭代次数J,迭代过程中OMP算法的稀疏度为L并初始化字典Dm×K,字典原子数目为K。
(2)利用OMP算法求解系数矩阵WK×n。
(3)随机排列字典原子序号,记为rperm,初始化计数器j=1。
(4)令h=rperm(j),找出系数矩阵W第h行中不为零的元素,记录其位置Ih={
α|W(h,α)≠0|}。
(5)若集合I为空,则计算误差矩阵E=Y-DW,并记录其最大误差所在列i,将数据集的第i列归一化作为字典的第h个原子,D(h)=Y(i)/‖Y(i)‖2;若集合I不为空,则根据集合中元素得到新系数矩阵WT=(k,α),(k=1,2,…,K;α∈Ih),并找到对应的数据列计算误差E=Y(α)-DWT,(α∈Ih),对误差奇异值分解得到左特征向量p、特征值s、右特征向量d,更新D(h)=d,W(h,α)=spT,(α∈Ih) 。
(6)更新计数器j=j+1,返回步骤(4),当j=K时停止。
(7)更新迭代次数返回步骤(3)直至算法结束。
改进后的算法只根据系数矩阵中不为零元素的位置对其部分字典基进行奇异值分解,加快了计算效率[14]。
2.2 稀疏编码
利用K-SVD学习算法学习得到的字典较其他字典稀疏性更好,能够以较少的系数准确表示数据的稀疏特征,可以对海量运行监测数据进行有效地压缩。相比时域样本信号,频域信号可以有效消除相同类型样本之间故障冲击时移的影响,故障模式识别的鲁棒性更好。因此,采用其频域数据进行处理。
利用K-SVD算法求取ELM模型输入的过程如下:①将数据库中所有数据进行频域转换,得到其频域数据;②将频域数据库分为数据集1与数据集2,使其2个数据集都均匀包含每种故障类型;③将数据集1作为K-SVD算法的样本数据学习得到字典D;④基于该字典使用OMP算法[15]分别求取数据集1和数据集2的稀疏系数矩阵作为训练集和测试集,根据故障类型赋予其标签,得到ELM的模型输入。
3 试验分析
为了说明此种模型输入的有效性与优越性,将此模型应用于实例分析。采用西储大学发布的轴承振动数据进行分析[16-17],选取其中10种故障类型的数据用于故障模式识别,并与其他模型输入方式结果进行对比。另外2种模型输入方式为:多种时、频域指标和PCA融合的特征指标,在同样的训练样本和测试样本基础上,从网络的诊断正确率、隐含层激活函数和神经元个数多个方面进行综合分析。同时为说明ELM模型的优越性,对比分析了以稀疏编码为输入的BP神经网络、SVM模型。
原始数据的具体信息见表1,该数据由轴承支座上放置的加速度传感器采集得到,采样频率为12 kHz。将单点损伤直径为0.177 8 mm的损伤定为一级损伤,单点损伤直径为0.355 6 mm的损伤定为二级损伤,单点损伤直径为0.533 4 mm的损伤定为三级损伤,并将其采集得到的数据不重叠地划分为118个,每个样本包含1 024个数据点,随机划分每种故障类型的样本组成训练样本和测试样本,样本间互不重复,训练样本包含每种故障类型70个,测试样本包含每种故障类型48个。
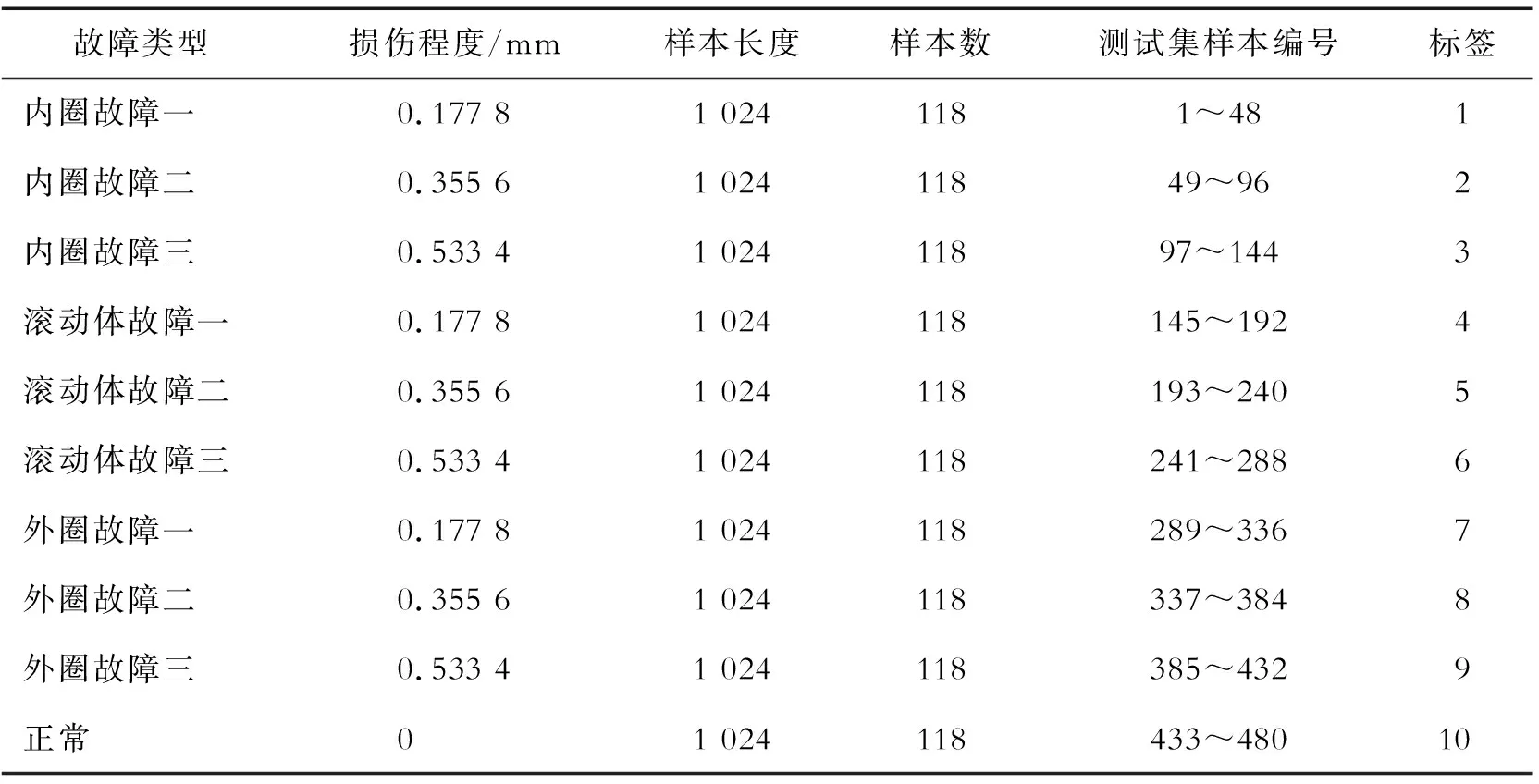
表1 数据信息
采用稀疏编码的方式对数据进行处理,首先对全部数据进行频域转换,使用训练样本作为K-SVD算法的学习样本,过程中,字典原子个数K设置为10,算法过程中OMP稀疏度L为5,迭代次数J为5。使用学习到的字典对全部频域数据进行稀疏编码,将每个样本数据的稀疏系数向量代替其样本作为ELM模型的输入。同时计算每个样本的时域、频域指标以及将时、频域指标进行PCA融合后的特征构建了其他2种模型输入。其中,时域指标选取为:最大值、均值、均方根值、方差、偏度、峭度、波形指标、脉冲指标;频域指标选取为:频率均值、频率标准差、频率均方根以及频谱峭度共12个指标;PCA融合后选择其前6个主元作为模型输入。
3种模型输入的测试集诊断结果如表2所示,其中固定神经元数量为40,为消除随机因素影响,每种模型输入计算30次。

表2 测试集诊断结果
从表2可以看出,稀疏编码为输入的诊断模型在3种激活函数下都取得了最高的平均正确率,以Sigmoid函数为激活函数时,其正确率最高,为98.57%,标准差也较小,仅为0.29%,诊断结果最为稳定。此外,以Sigmoid函数为激活函数时,3种模型输入均取得了最高的平均正确率和最低的正确率标准差,相比于其他激活函数,此函数具有更强的鲁棒性。因此,基于Sigmoid函数分析隐含层神经元数量对测试集诊断结果的影响。
极限学习机的隐含神经元数量不仅影响模型的诊断正确率,还关系到模型的计算时间。较少的神经元不能有效提取数据特征,过多的神经元则会造成数据冗余,同时增加计算负担。基于Sigmoid函数分析神经元数量对测试集诊断结果的影响,在1~400每种神经元个数下计算3种模型输入诊断结果30次,其平均正确率结果如图2所示,正确率标准差如图3所示。由图2、图3可知,3种模型输入的诊断正确率随神经元个数的增加都呈先增加后下降的趋势,PCA主元作为模型输入的平均正确率较时、频域指标略高,但这2种模型输入的诊断平均正确率在其稳定区域(即随神经元个数增加、平均正确率未出现明显下降的区域)均低于以稀疏编码为输入的模型。并且在较宽的神经元个数范围内(20~200),以稀疏编码为输入的模型诊断平均正确率均稳定在98%以上,标准差稳定在1%以下,可见该诊断模型不仅具有较高的正确率,稳定性也较好。
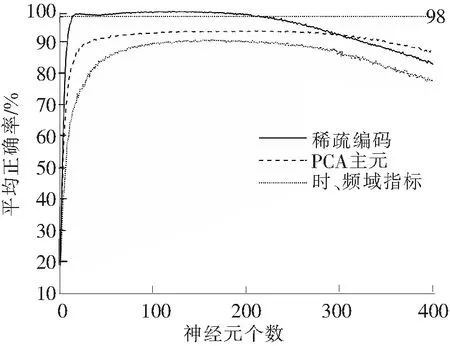
图2 平均正确率分析
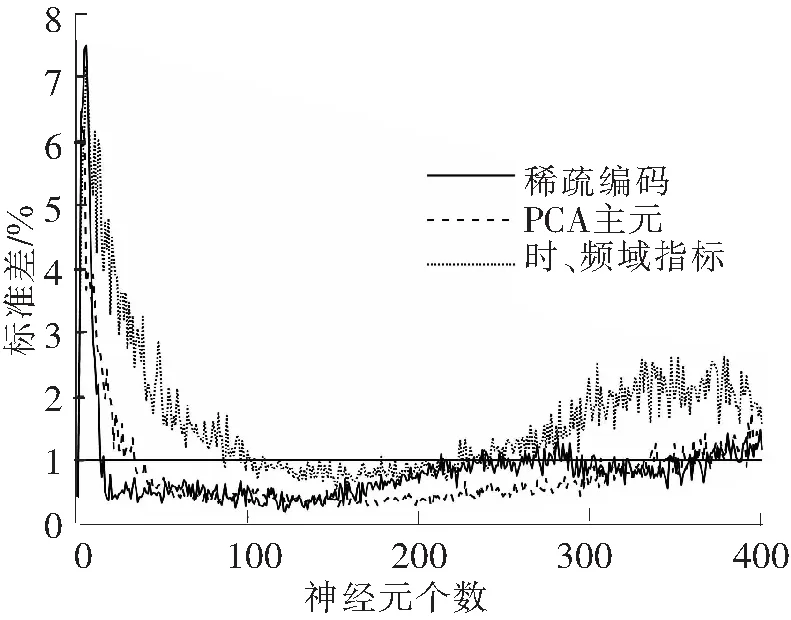
图3 标准差分析
以Sigmoid函数为激活函数、隐含层神经元数量为100时,3种模型输入的诊断结果分别见图4~图6。稀疏编码为输入时,仅有1个样本诊断错误,明显低于其他2种输入的模型,诊断效果非常明显。
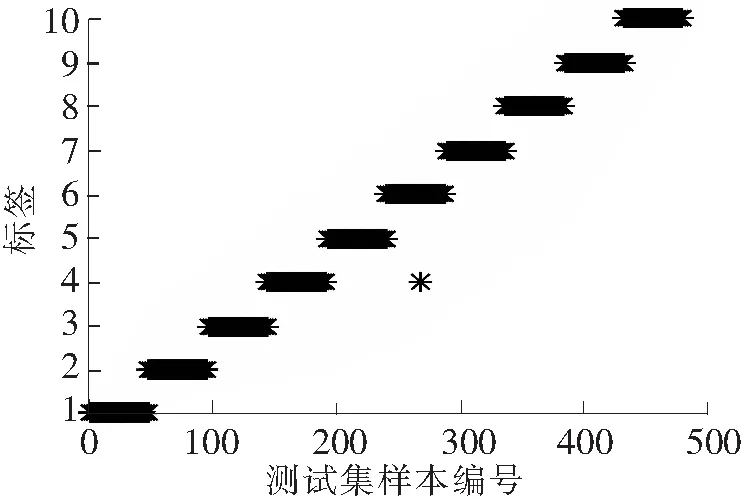
图4 稀疏编码为输入的诊断结果
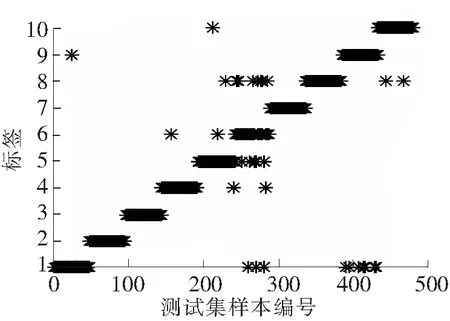
图5 PCA主元为输入的诊断结果
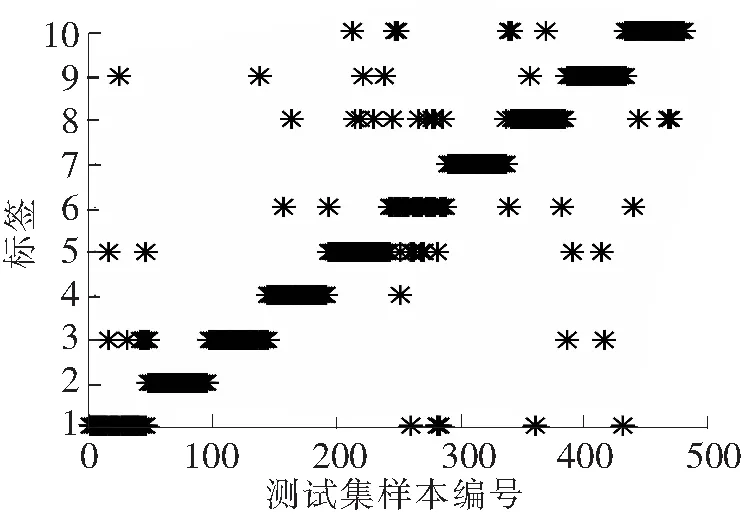
图6 时、频域指标为输入的诊断结果
将稀疏编码作为输入,采用BP神经网络、SVM模型进行故障模式识别。不断调整2种方法参数,确定其最优参数如下:BP神经网络隐含层神经元数量为10,学习率为0.1,最高迭代次数为10 000,隐含层激励函数为“Sigmoid”;SVM核函数类型为“linear”。ELM模型的隐含层神经元数量为100,激活函数为“Sigmoid”。3种模型每种模型计算30次,测试集诊断结果见表3。测试平台计算机的配置为:CPU是酷睿i5-4210(2.4 GHz),8 G内存,Matlab软件版本为R2016a。
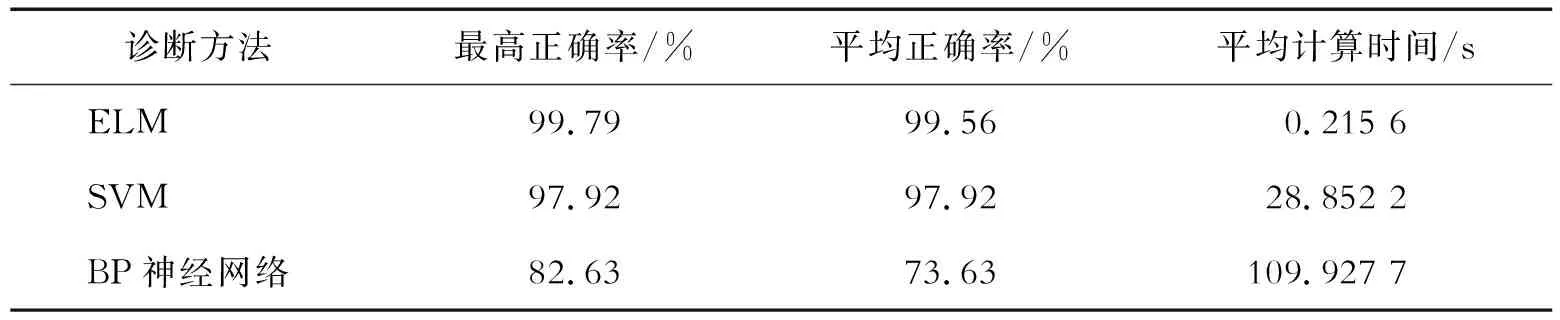
表3 测试集诊断结果
从表3的诊断结果可以看出,以稀疏编码为输入的ELM模型不仅具有极高的正确率,同时计算时间相对最短,满足实际工程应用需要。相比传统的BP神经网络、SVM等方法,ELM建立能反映特征值之间复杂关系的非线性高斯函数模型,进而准确反映不同特征值之间复杂关系,可以对待测样本进行更加准确的样本识别。
4 结论
(1)提出了以稀疏编码为输入的ELM诊断模型,将其应用于10种不同类型、不同程度滚动轴承故障进行模式识别,并与其他2种输入的ELM模型、BP神经网络、SVM模型对比。结果表明,以稀疏编码为输入的ELM模型诊断正确率更高,稳定性也较好,并且模型保持了ELM计算速度快的优点。
(2)隐含层激活函数为Sigmoid、神经元数量为20~200时,以稀疏编码为输入的ELM诊断模型平均正确率稳定在98%以上,标准差稳定在1%以下,较强的诊断性能使其更适用于设备故障诊断。
