单位球上加权Bergman空间到Zygmund型空间上的积分型算子
2020-02-21赵艳辉廖春艳邓春红
赵艳辉, 廖春艳, 邓春红
(1.湖南科技学院理学院, 湖南永州 425199)
(2.湖南科技学院理学院计算数学研究所, 湖南永州 425199)
1 引言
设B表示Cn上的单位球,∂B 表示单位球面,dv为标准体测度, 满足v(B) = 1,dσ为标准面测度, 满足σ(∂B)=1,H(B) 代表B上的全纯函数类.
定义1.1设0
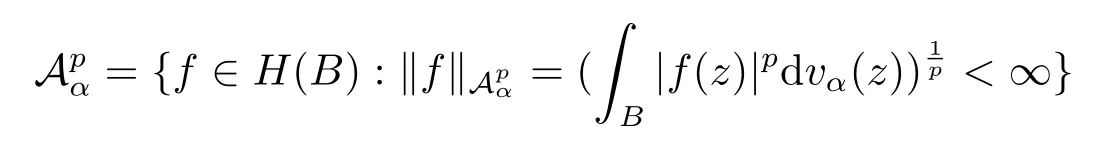
表示B上的加权 Bergman 空间其中
当 1≤p<∞时,在范数下是一个 Banach 空间.当 0 定义1.2设[0,1) 上的连续函数µ(r)>0, 如果存在常数0 设µ为[0,1) 上的正规函数,f ∈H(B), 这里∇f表示f的复梯度,由文献 [1]知等价. 设µ为 [0,1) 上的正规函数, 称f属于βµ空间是指:空间在范数 下是一个Banach 空间. 由文献 [2]中的引理 2.1 可知, 设µ为 [0,1) 上的正规函数, 称f ∈βµ当且仅当 定义1.3设µ为[0,1) 上的正规函数,B上的全纯函数f如果满足 则称f属于Zygmund 型空间则称f属于小 Zygmund 型空间(见文献 [3–5]).如果µ(r)=1−r2, Zygmund 型空间(小 Zygmund 型空间就是典型的Zygmund 空间Z(小Zygmund 空间), 这里R(2)f(z)=R(Rf(z)). 定义1.4设ϕ是B上的全纯自映射,g ∈H(B) 且g(0)=0, 则由ϕ和g诱导的H(B)上的算子定义为 文献[3–11]研究了该类算子的性质.若用Rg代替g, 且ϕ(z) =z, 算子Pg就是加权算子, 它在文献[12]被引入并研究, 文献[13–16]对几个全纯函数空间上的加权算子的有界性和紧性进行了讨论.关于Bergman 空间上的复合算子和算子的有界性和紧性问题的讨论得到了一些很好的结论, 如文献[1,2,16–18]. 本文的主要工作就是在Cn中的单位球上来给出空间到型空间上的有界算子和紧算子的充要条件.同时分别得到了单位圆盘D上和ϕ(z) =z时单位球上的相应结论.本文中用记号c,c1,c2来表示与变量z,ω无关的正数,c,c1,c2可以与某些范数或有界量有关, 不同的地方可以表示不同的正常数. 引理2.1[7]设f,g ∈H(B),g(0)=0, 则 引理 2.2[2]设则 引理2.3设0 证由引理2.2 和Montel 定理按定义可证. 引理2.4[3]中的闭子集K是紧子集的充要条件是K是有界集, 且满足 定理3.1设0 这里Jϕ(z) 是ϕ(z) 的 Jacobi 矩阵, 且 证 充分性设(3.1) – (3.2) 成立, 则由和引理2.1–2.2 有 必要性设空间到Zµ型空间的有界算子.取则由和βµ的定义可知g ∈βµ,gϕl ∈βµ(l=1,2,···,n). (1) 先证 (3.1) 式成立.∀ω ∈B,u ∈Cn −{0}. 则fω(ϕ(ω))=0, 且由文献 [19]中的定理 1.12 有 则fω(ϕ(ω))=0, 且由文献 [20]中的命题 1.4.10 有 所以类似(3.5) 式的证明, 结合(3.6) 式有 下面证明(3.2) 式成立.取 所以(3.2) 式成立. 综上所述, 定理3.1 得证. 当ϕ(z)=z时, 易知下列结论成立. 推论 3.2设 0 而对于单位圆盘则有以下结论成立. 推论 3.3设 0 定理3.4设0 证 充分性假设(3.8)和(3.9)式成立,则对任意ε>0,存在0<δ<1,当|ϕ(z)|2>1−δ时, 设{fj} 是在B的任一紧子集上一致收敛于0 并满足的全纯函数列, 则 {fj}和 {∇fj} 在E={ω:|ω|2≤1−δ} 上一致收敛于 0. 若 |ϕ(z)|2>1−δ, 由 (3.10)–(3.11) 式及引理 2.2, 有 若|ϕ(z)|2≤1−δ,因为g ∈βµ,gϕl ∈βµ,所以由{fj} 和{∇fj} 在E={ω:|ω|2≤1−δ}上一致收敛于0, 有 注意到{g(0)fj(ϕ(0))}一致收敛于0,结合(3.12)式和(3.13)式,有0, 从而根据引理2.3 知空间到Zµ型空间的紧算子. 必要性设空间到Zµ型空间的紧算子, 由有界性的证明知g ∈ βµ,gϕl ∈ βµ. 假设 (3.8) 式不成立, 则存在 {zj}⊂B,{uj}⊂Cn −{0} 和常数ε0> 0, 使得rj=|ϕ(zj)|→1(j →∞), 有 则fj(ϕ(zj))=0.类似定理 3.1 中的证明易知 下面证明{fj} 在B的任一紧子集E ⊆{z:|z|≤r},0 所以{fj} 在B的任一紧子集上一致趋于0.但由(3.14) 式, 类似定理3.1 中的证明有 则fj(ϕ(zj)) = 0.经计算易知且 {fj} 在B的任一紧子集E ⊆{z:|z|≤r},0 下面证明(3.9) 式成立.假设(3.9) 式不成立, 则存在{zj}⊂B和常数ε0> 0, 使得|ϕ(zj)|→1(j →∞), 有 当ϕ(z)=z时, 易知下列结论成立. 推论 3.5设 0 而对于单位圆盘则有以下结论成立. 推论 3.6设 0 定理 3.7设 0 证因为紧算子是有界算子, 所以(1)⇒(2) 成立, 由空间的定义及定理3.4 知(2)⇒(3) 也成立.再证 (3)⇒(1), 先证 (3)⇒(2).由定理 3.4, 对任意的类似于定理3.1 中充分性的证明有 再证(3)⇒(1).若条件(3) 成立, 则条件(2) 成立.集合在空间中是有界的, 由定理3.4 并结合(3.19) 式有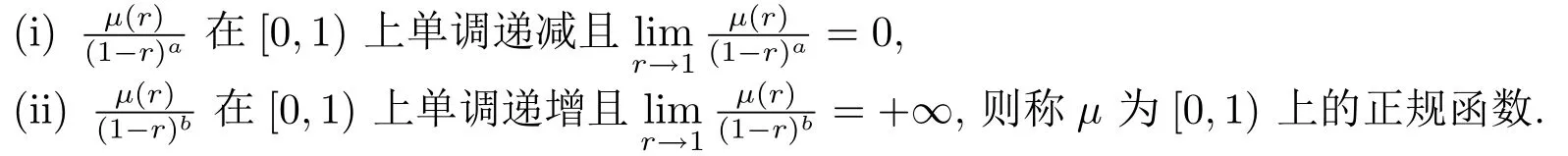
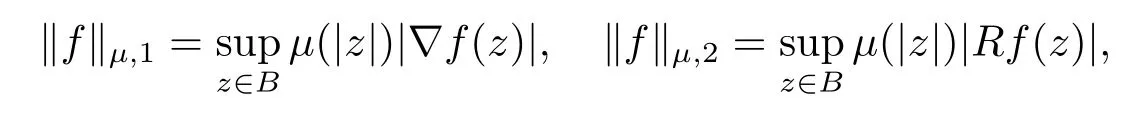
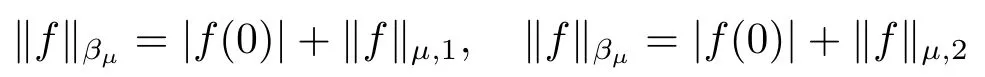
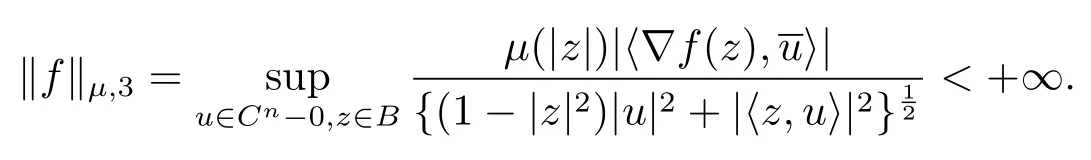
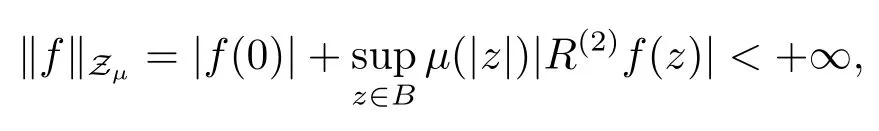
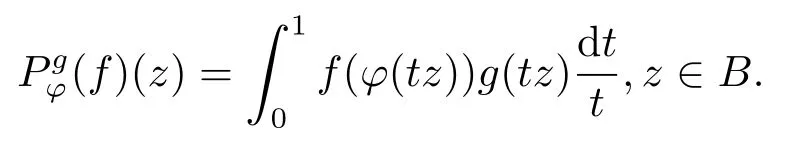
2 有关引理
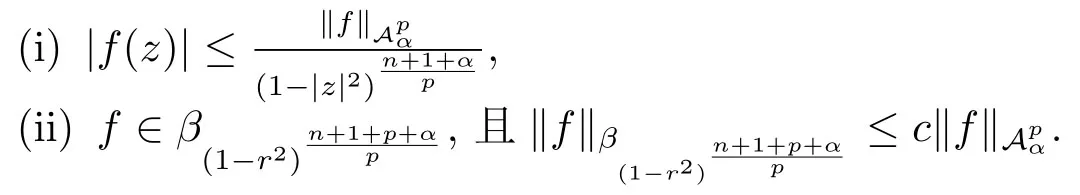
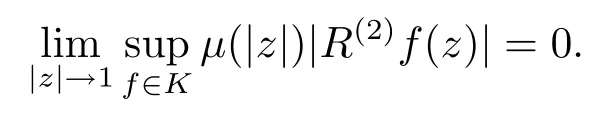
3 主要结果
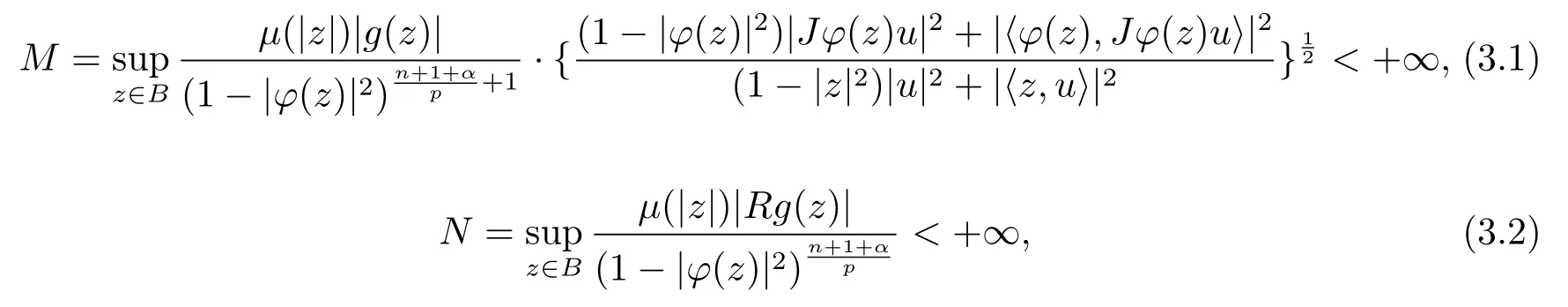
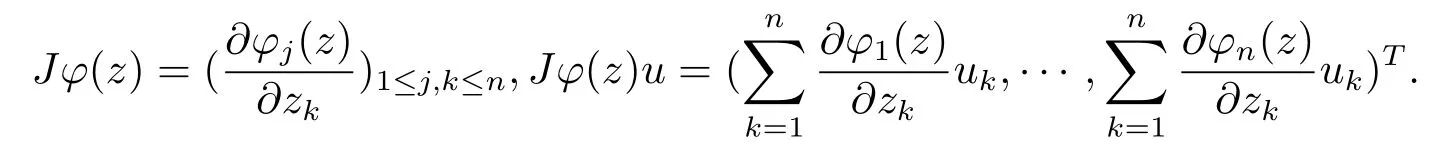
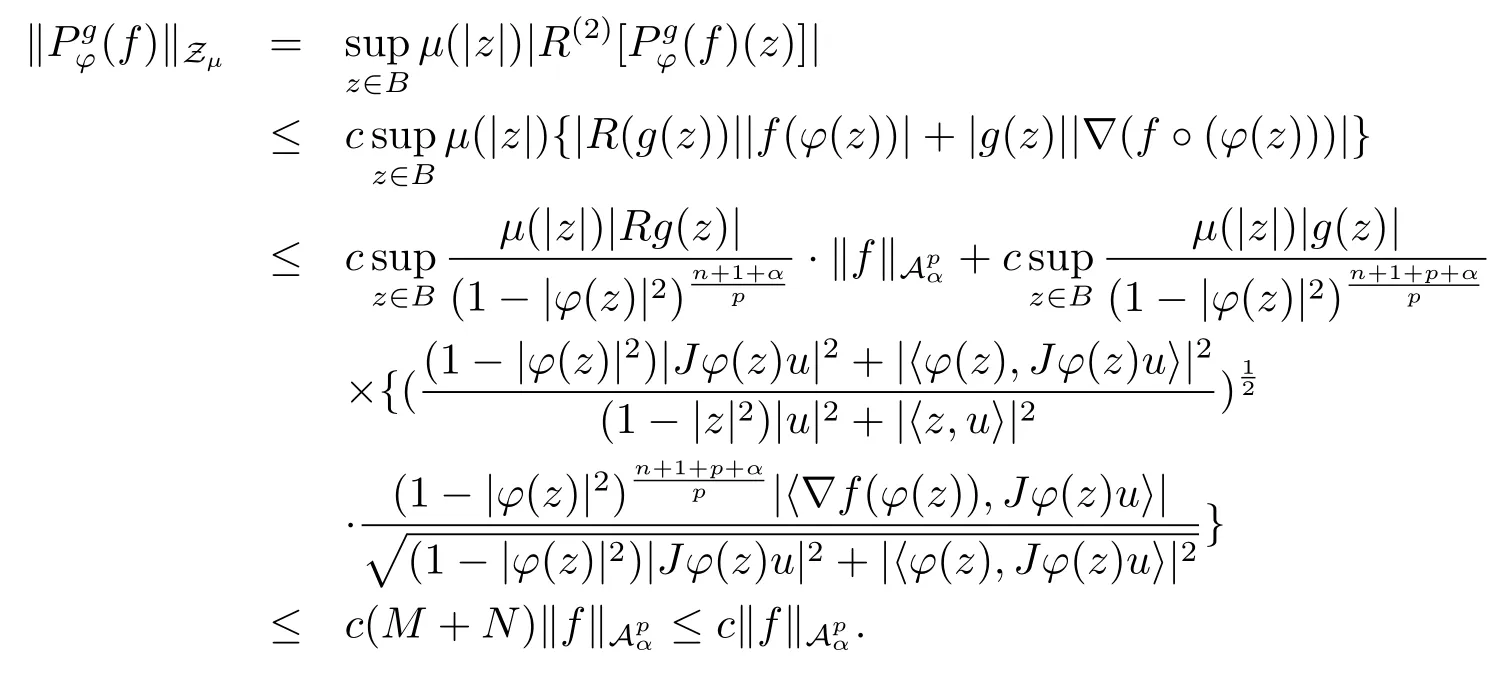
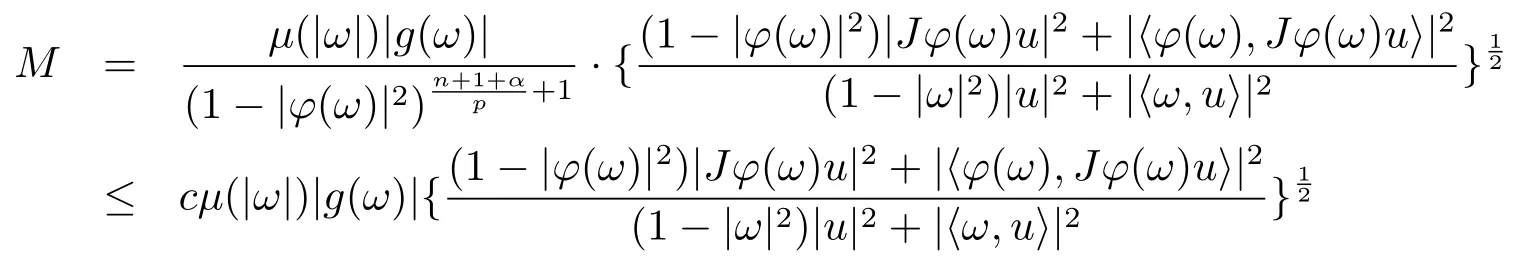
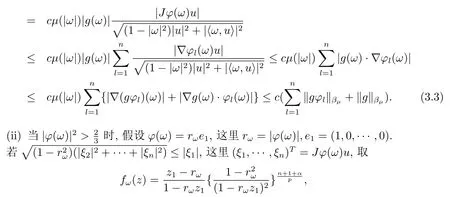

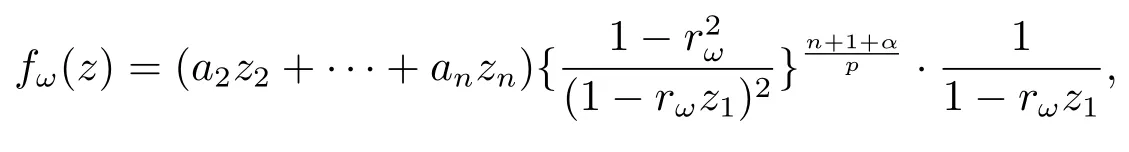

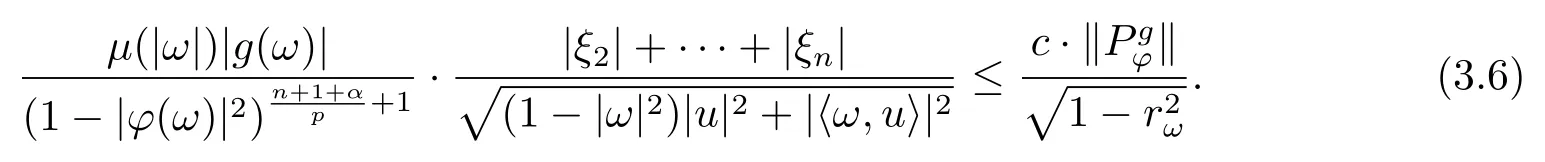
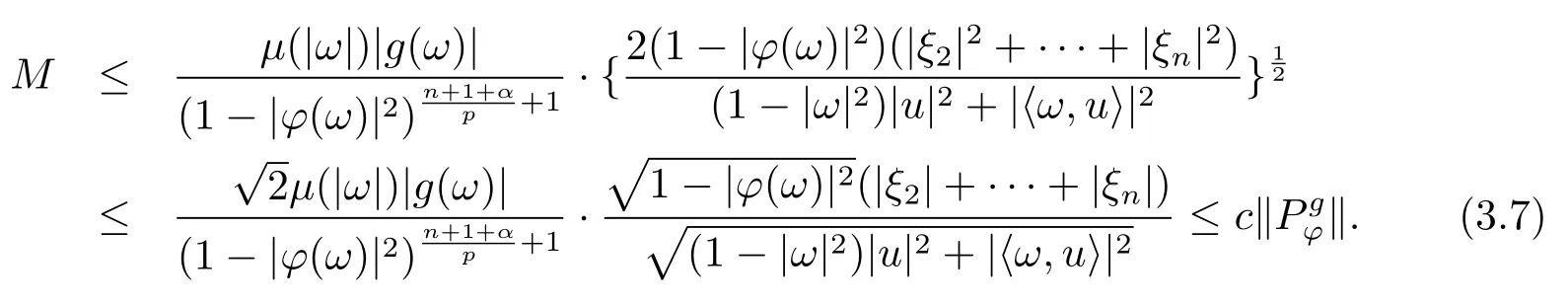
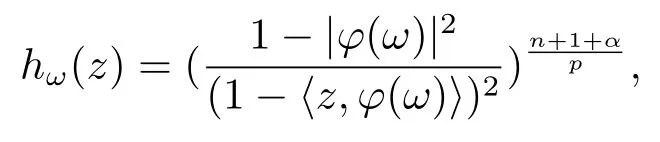
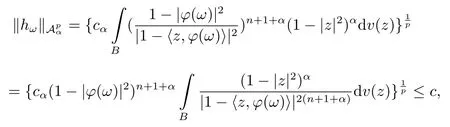
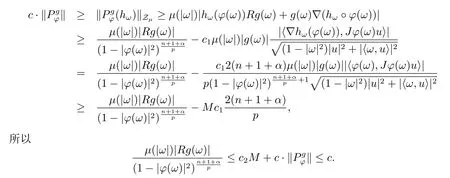
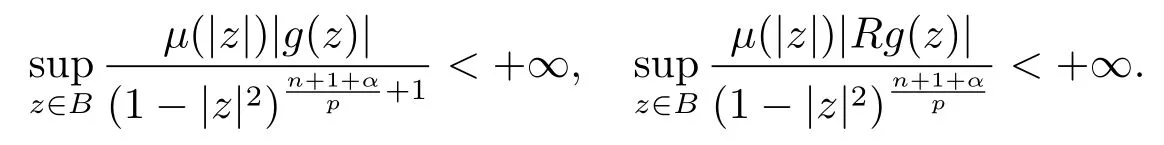
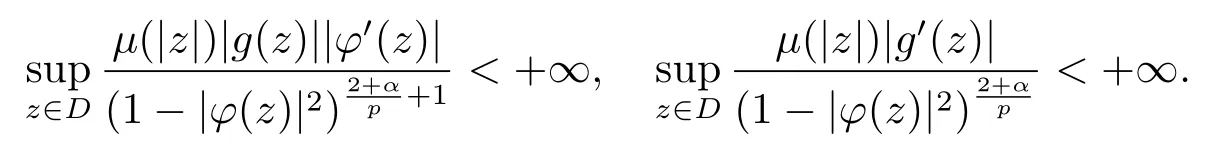
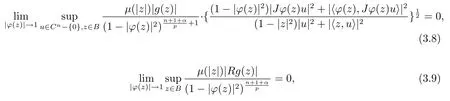
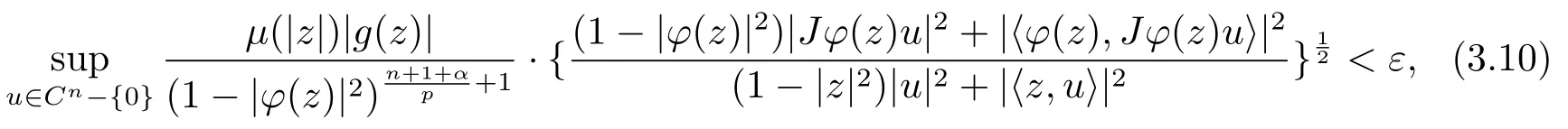

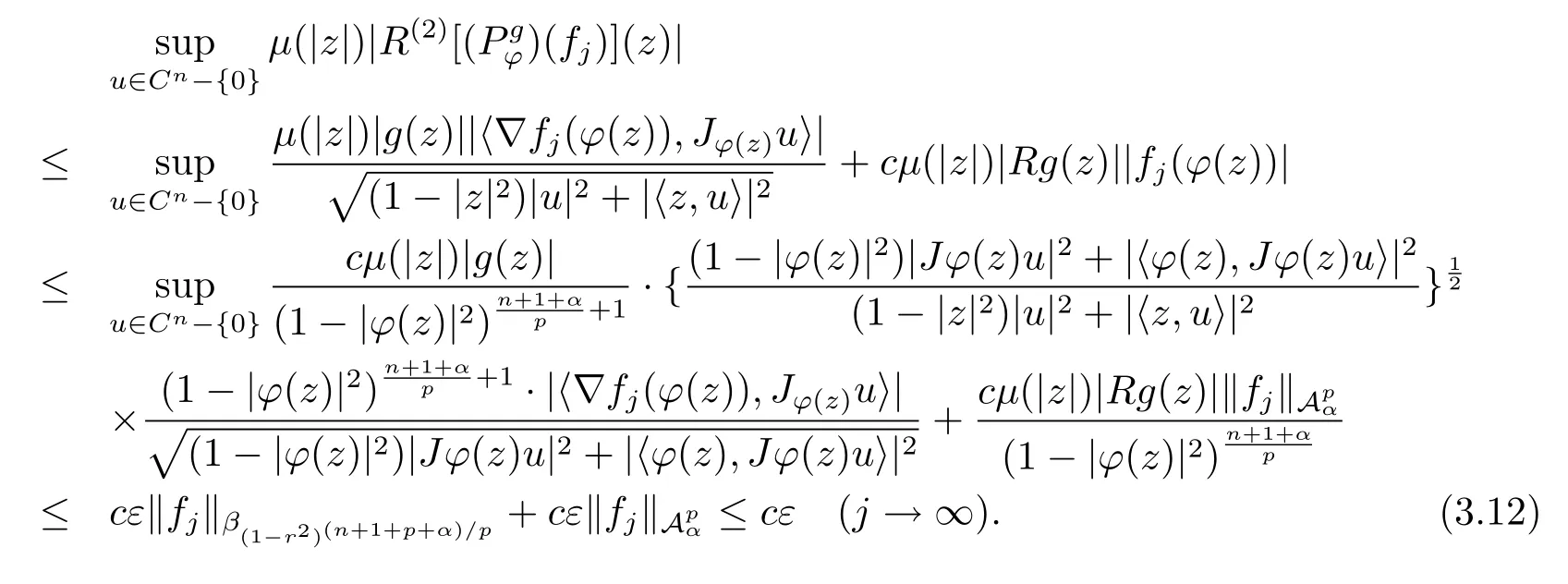
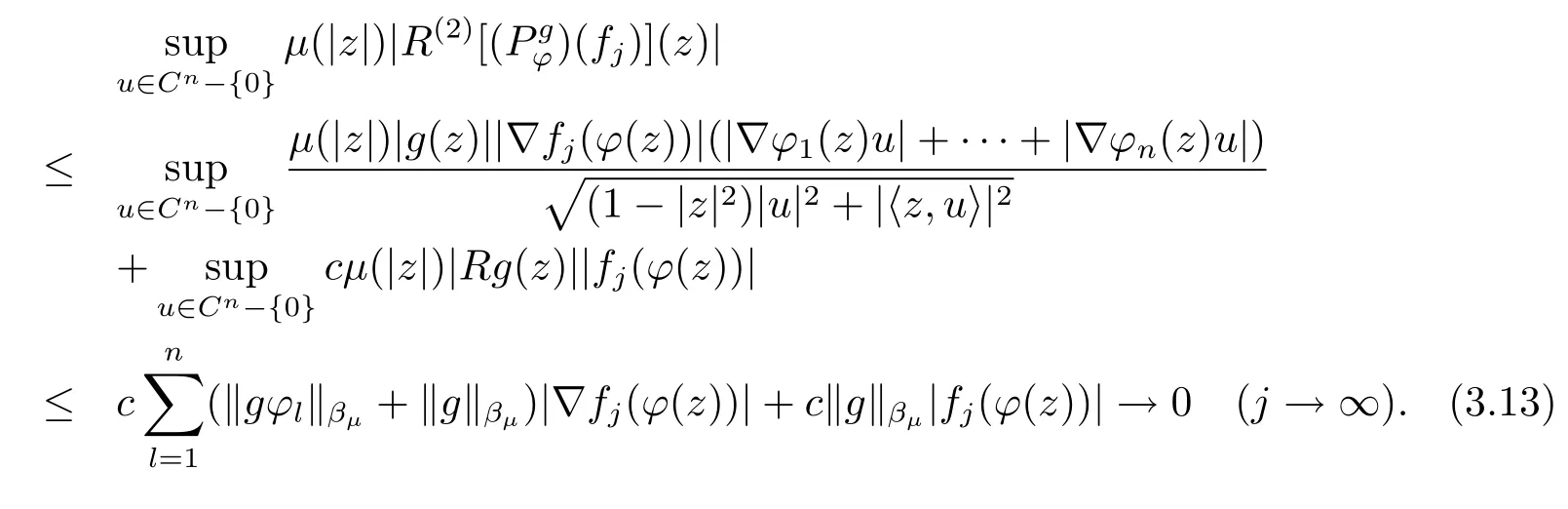
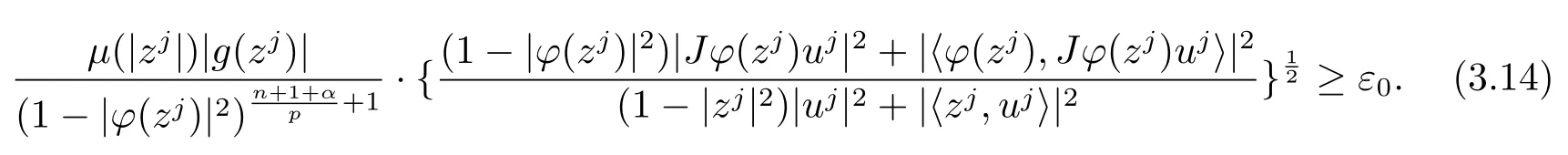
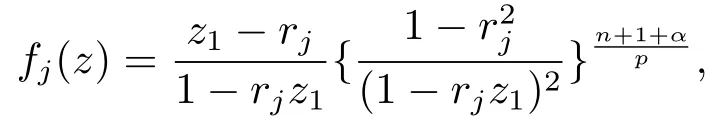
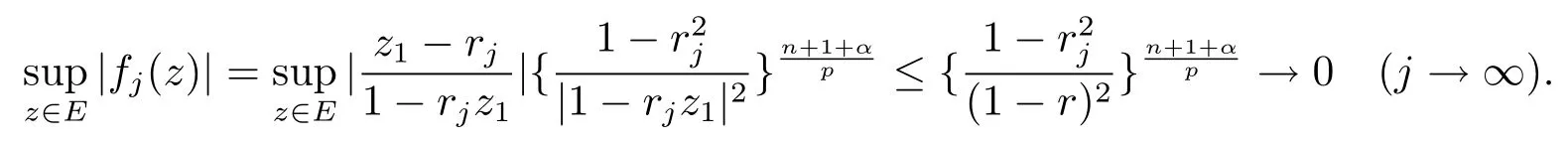
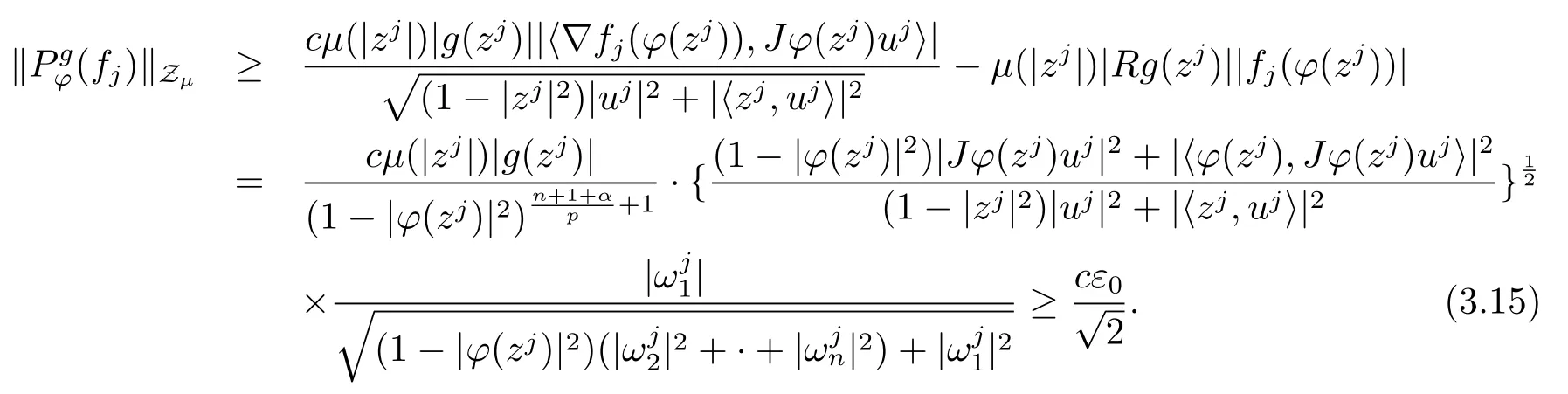
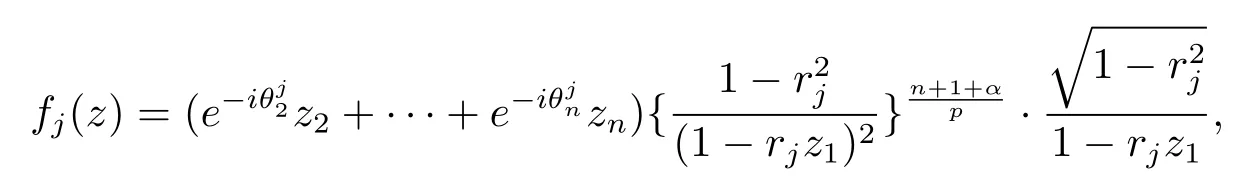
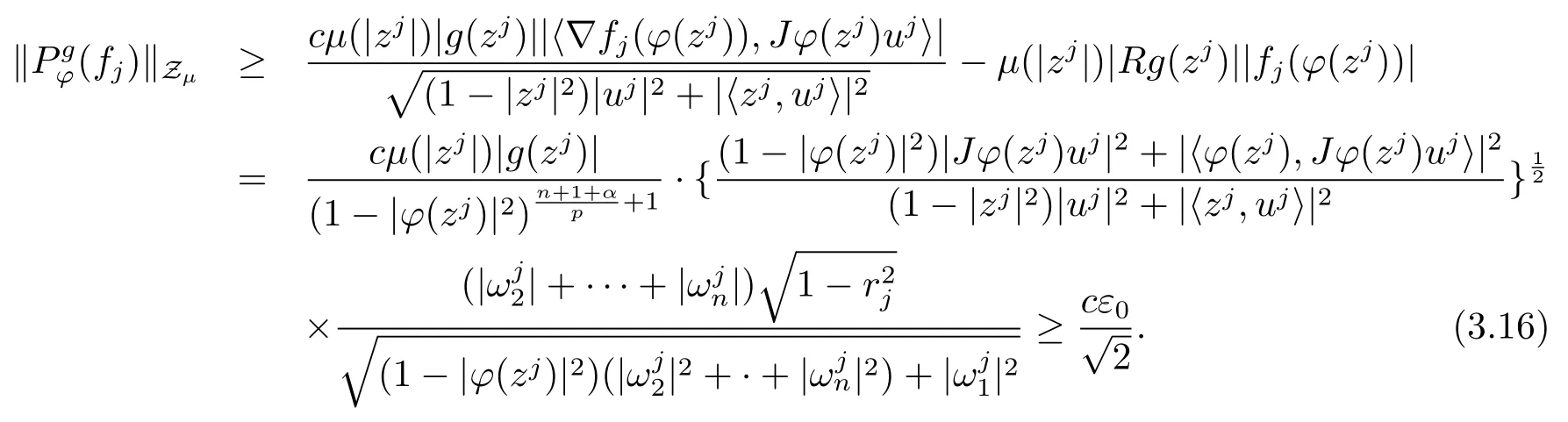
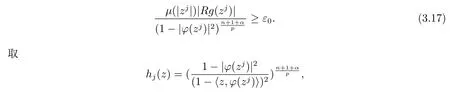

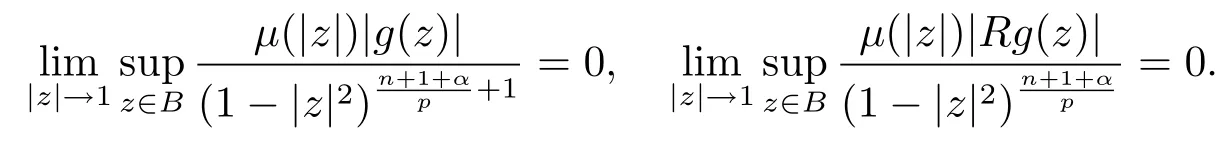
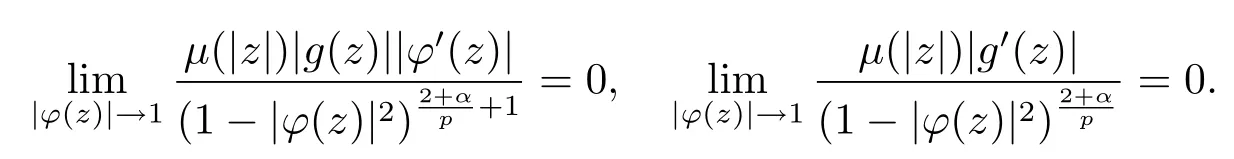
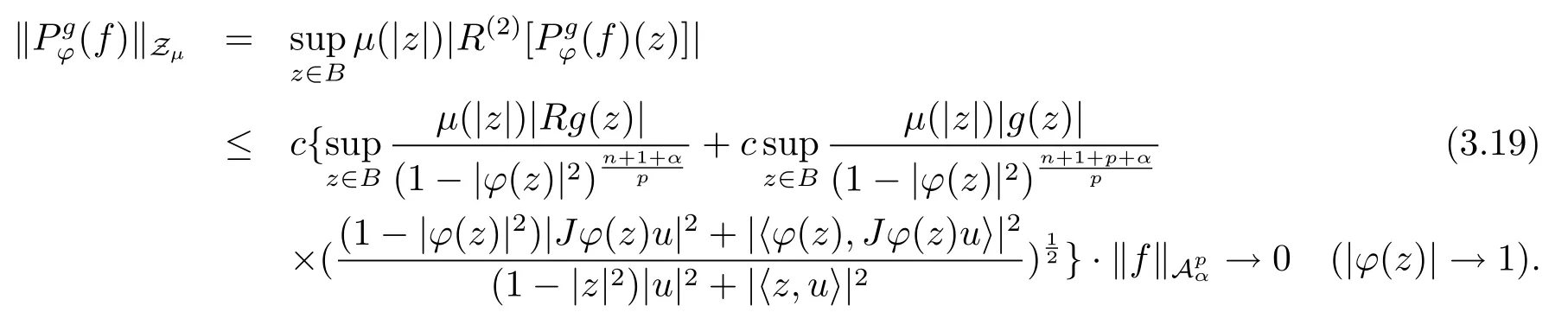
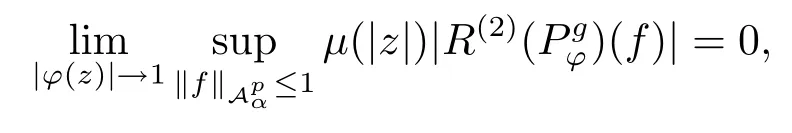
猜你喜欢
杂志排行
数学杂志的其它文章
- LEONARD PAIRS CONSTRUCTED FROM THE QUANTUM ALGEBRA νq(sl2)
- BOUNDEDNESS OF THE FRACTIONAL INTEGRAL OPERATOR WITH ROUGH KERNEL AND ITS COMMUTATOR IN VANISHING GENERALIZED VARIABLE EXPONENT MORREY SPACES ON UNBOUNDED SETS
- IMPROVE INEQUALITIES OF ARITHMETIC-HARMONIC MEAN
- A CLASS OF NON-MATCHABLE DISTRIBUTIVE LATTICES
- SHARP ESTIMATES FOR EIGENVALUES OF BI-DRIFTING LAPLACIAN
- 素的∗-代数上的非线性混合Lie三重ξ-导子
