串联节点刚度对隔振系统传递率的影响研究
2020-02-20董大伟华春蓉
王 群,董大伟,华春蓉,黄 燕
(西南交通大学 机械工程学院,四川 成都 610031)
1 引言
机械振动会引起动力机械的零部件损坏,影响精密仪器的工作效果,甚至对人体产生不良影响。在动力机械领域中,多采用隔振元件来降低振动部件传递到设备的传递力和振动烈度,隔振元件的选用、连接方式和性能关系到整个系统的工作稳定性和可靠性[1]。隔振系统元件类型、参数对隔振性能的影响已有许多学者进行了大量研究,得到了许多有参考价值的结果,如文献[2]分别用模态分析法和摄动法得到了隔振系统线性和非线性方程组的响应解,文献[3]从隔振系统参数变化对功率流特性影响的角度研究了系统的隔振效果,文献[4]基于快速摄动法研究了参数变异对双层隔振系统隔振效率的影响规律,文献[5-6]对隔振系统解耦优化和刚度优化进行了研究,文献[7]建立了普通双层隔振系统多体动力学模型,仿真分析了理论力的传递率特性。诸多学者的研究多是针对隔振器本身特性参数对系统的影响,且理论模型多做简化,即未考虑串联节点刚度对隔振系统的影响。
目前常用的隔振系统包含刚度元件和阻尼元件,典型的刚度元件如橡胶隔振器、弹簧隔振器等,典型的阻尼元件如材料阻尼器、油压减振器等。由于油压减振器制造简单、价格便宜,且阻尼系数便于设计和调整,故其广泛应用于动力机械隔振系统中。而在工程实践中,减振器的端部节点或液压油本身具有一定的弹性,所以,实际上减振器应当被看成一个阻尼元件和刚度元件的串联组合,该刚度元件通常被称为串联节点刚度。在运用减振器的诸多领域,串联节点刚度对系统的影响已然引起学者们的关注,如文献[8]初步探讨了串联刚度对液压减振器特性的影响,文献[9]研究了减振器安装刚度对车辆固有频率的影响,文献[10]研究了抗蛇形减振器的特性参数对其车辆动力学稳定性的影响,文献[11-12]研究了减振器橡胶节点刚度对铁道车辆系统临界速度的影响。但是在动力机械的隔振运用方面,大多数研究均未考虑串联节点刚度对系统隔振性能的影响,而在实际应用中,减振器串联节点刚度确实存在,且对其阻尼特性有一定影响[8],阻尼特性的改变势必影响隔振性能。为解决上述问题,以包含减振器串联节点刚度的隔振系统为研究对象,分析其串联节点刚度对隔振系统传递率的影响,并加以实验验证,为变刚度隔振系统提供理论依据,也为应用于隔振系统的减振器性能优化设计提供参考。
2 考虑串联节点刚度的减振器动力学模型
根据动力学理论,建立考虑串联节点刚度的液压减振器动力学模型,如图1所示。

图1考虑串联节点刚度的液压减振器模型[8]Fig.1 The Dynamics Model of a Hydraulic Shock Absorber Considering the Series Joint Stiffness
图1 中,k1是减振器的串联节点刚度,c是减振器的阻尼系数。当有外力F作用于减振器时,减振器端部A的位移为x,节点B的位移为y。
力学平衡方程为:

设减振器端部位移激励为:

则端部运动速度为:

式中:x0—位移激励的振幅;
ω—激励圆频率。
对于图1的常系数线性系统,B点的稳态响应的位移和速度是:

式中:y0—串联弹簧位移的振幅;
φ—串联弹簧位移的相位。
将式(3)、式(4)和式(5)代入式(1),并整理可得减振器的实际阻尼力幅值:

从式(6)中可以看出,串联刚度后的减振器实际输出阻尼力幅值与串联节点刚度k1、减振器阻尼系数c、激励圆频率ω和位移激励的振幅x0有关;当k1足够大时,即端部近似刚性连接,减振器的实际阻尼力幅值为F0=cωx0;当k1足够小时,减振器的实际阻尼力幅值为F0=x0。此理论模型的变化曲线,如图2所示。其中激励频率取10Hz,阻尼系数1000N/(m/s),刚度变化范围10-6×106N/m。

图2 阻尼力随串联刚度变化曲线Fig.2 Damping Force Curve with Variation of Series Stiffness
从图2可以看出,当串联节点刚度小于2×105N/m时,阻尼力的幅值从0.05N逐渐增加至600N;当串联节点刚度大于3×105N/m后,阻尼力幅值约624N,且基本保持不变。
根据相关文献[13],常规减振器端部橡胶衬套的Z向刚度即串联节点刚度约4.2×106N/m,结合图2,该刚度下减振器的输出阻尼力基本恒定,符合工程需求。但是实际应用中,未考虑小刚度衬套下的阻尼力特性,将小刚度和大刚度特性结合加以考虑,为变刚度节点的研究提供理论基础。
3 隔振系统动力学模型及传递率计算
3.1 动力学模型建立
将动力机械隔振系统简化为单质量隔振系统,如图3所示。上层质量m为需要隔离的动力机械,激振力设为Fsinωt,设隔振器的刚度为k,减振器的阻尼系数为c,减振器串联节点的刚度为k1(下文均称串联刚度)。结合上节建立的减振器的力学平衡关系,列出系统的强迫振动微分方程组为:

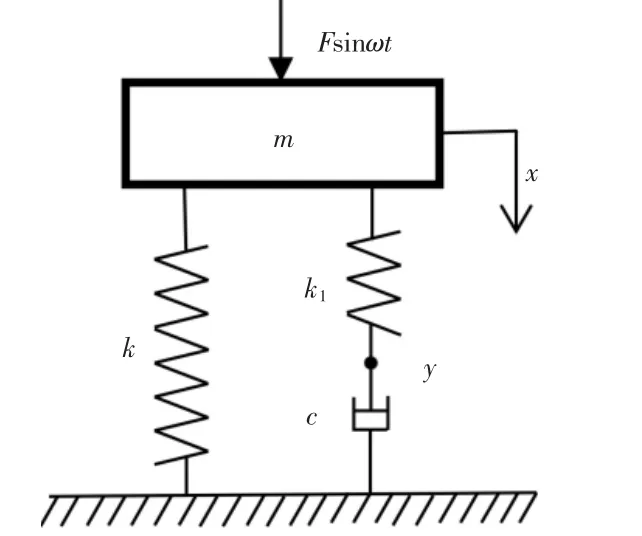
图3 单层隔振系统模型Fig.3 The Dynamics Model of Single-Layer Vibration Isolation System
3.2 数值求解
考虑隔振系统的瞬态响应由阻尼作用,会很快消失,因此只考虑稳态响应来描述系统特性,采用复数矢量表示法,首先设x=Bei(ωt-φ)和y=Aei(ωt-φ)代入式(8)化简可以得到:

以 Feiωt表示式(7)等号右边的激振力,并将式(9)带入式(7)得到:

由式(10)解出 B:

将式(11)带入式(9),解出 A:

因此,m的位移响应为:

节点的位移响应为:
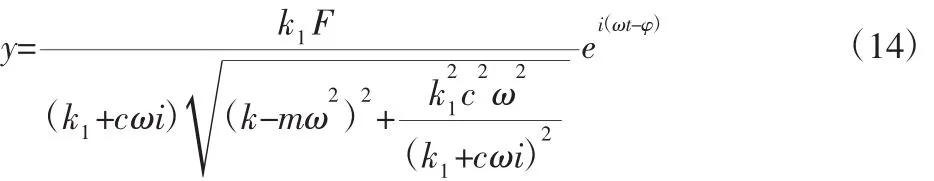
从上两式可以看出,节点的位移和上层质量的响应相位相同,但在数值上相差
当串联刚度k1远大于cω时,m的位移响应和节点的位移响应近似相等为:
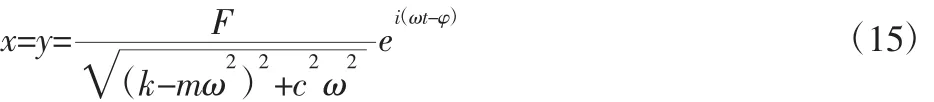
当串联刚度k1远小于cω时,m的位移响应和节点的位移响应分别为:
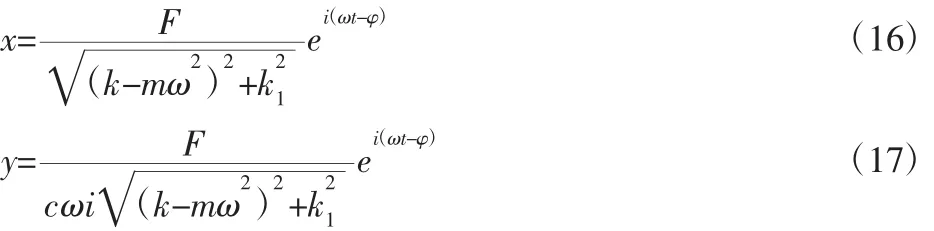
m的振动速度和节点的速度分别为:
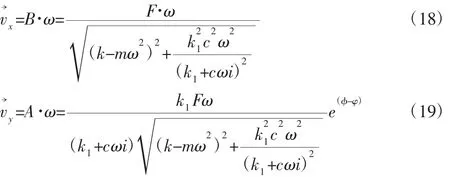
考虑弹性力和阻尼力影响的传递率公式如下:

在不考虑相位的情况下,整理得到传递率表示为:
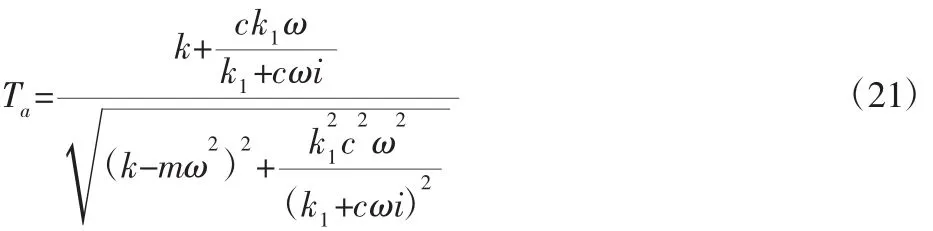
从上式可以看出,串联刚度对传递率有明显影响。当串联刚度k1远大于cω时,系统的传递率为:

当串联刚度k1远小于cω时,系统的传递率为:

4 仿真及实验验证
4.1 仿真及实验的对象简介
为了进一步讨论上述理论和规律,以某动力机组实验台为研究对象,对串联刚度和传递率之间的规律分别进行编程分析和实验验证,仿真及实验台的模型和测点布置,如图4所示。实验台采用4100Q直列四缸四冲程汽油发动机,机组与基础之间安装隔振器和减振器。实验主要验证了转速1200r/min以上的工况,1200r/min对应基频20Hz,2.0主简谐对应激励频率为40Hz,该转速对应的频率高于隔振系统固有频率。
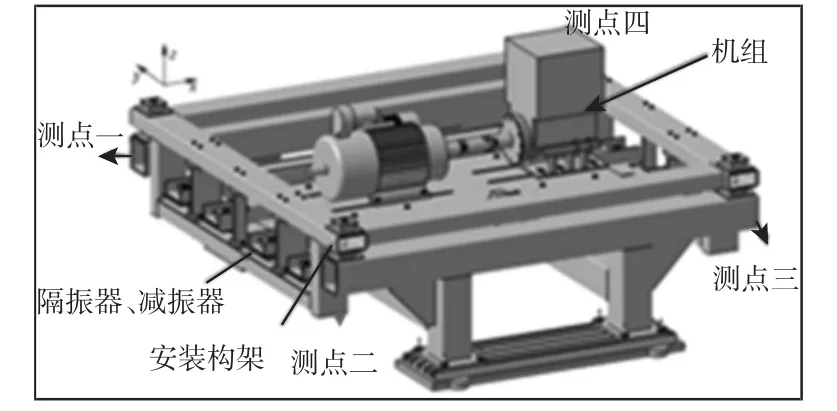
图4 实验台模型和测点布置Fig.4 Experimental Model and Measuring Point Arrangement
4.2 仿真分析
经仿真分析,得到随频率变化串联刚度和传递率之间的变化关系,如图5所示。从图5可知,当串联刚度k1远大于cω时(即k1=1000cω),与k1=cω相比,在共振区附近,传递率基本不变,在过共振区,传递率随串联刚度增大有所增大。当串联刚度k1远小于cω时(即k1=0.001cω),与k1=cω相比,传递率在共振区附近明显放大,在过共振区,传递率随串联刚度减小明显减小,隔振效率显著提高。

图5 串联刚度和对传递率的影响Fig.5 Effect of Series Stiffness and on Transmissibility
当串联刚度k1是隔振器刚度k倍数时,随频率变化传递率的变化曲线,如图6所示。从图6中可知,当串联刚度k1远大于系统隔振器刚度k时(即k1=1000k),与k1=k相比,在共振区附近,传递率基本不变;在过共振区,传递率随串联刚度增大明显增大。当串联刚度k1远小于系统隔振器刚度k时(即k1=0.001k),与k1=k相比,在共振区附近,传递率明显放大,在过共振区,传递率随串联刚度减小稍有减小。
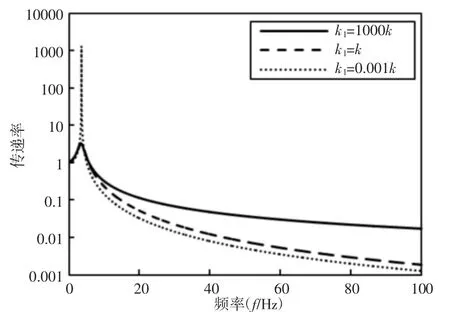
图6 串联刚度和隔振器刚度对传递率的影响Fig.6 Effect of Series Stiffness and Vibration Isolator Stiffness on Transmissibility
4.3 实验验证
本实验通过改变减振器端部节点的串联弹簧刚度,来分析串联刚度对隔振系统传递率的影响。实验中均采用松夏公司ZTA型弹簧隔振器,垂向刚度约3.86×105N/m,减振器为某型车辆减振器,机组从1140r/min按120r/min步长逐档加速到2100r/min。方案一中减振器端部采用串联小刚度弹簧的方式,计算刚度为4.1885×104N/m,方案二中减振器端部采用串联常规大刚度橡胶衬套的方式,两种方案的对比可反映串联刚度对传递力的影响。不同方案的发动机激振力传递到构架的传递力随激励频率变化的色谱图,如图7、图8所示。此传递力为各个测点各个方向(X/Y/Z三向)的平均值。从图7和图8中可以看出,方案一的最大传递力在激励频率(19~21)Hz附近为88.79N,方案二的最大传递力在激励频率(25~27)Hz附近为177.47N。同时从其余各频率段色谱图颜色的深浅明显看出,端部串联小刚度弹簧的方案一较常规大刚度橡胶衬套的方案二传递的传递力少,隔振性能更优。验证了上述简化的动力学模型以及仿真计算分析的正确性。

图7 方案一-端部串联小刚度弹簧Fig.7 Plan 1-Endconnected in Series by Small Stiffness Spring
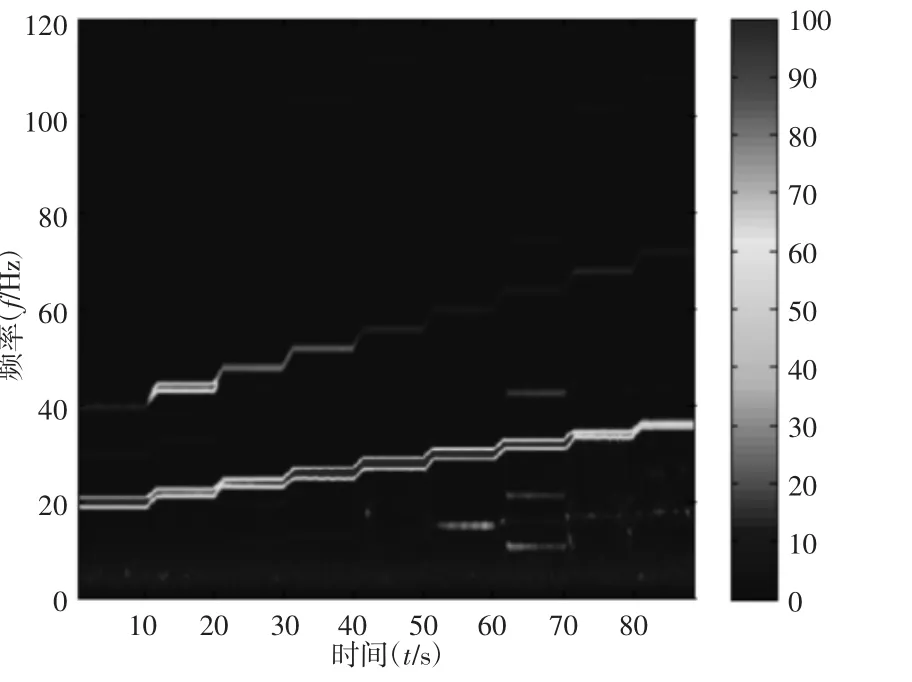
图8 方案二-端部串联大刚度橡胶衬套Fig.8 Plan 1-Endconnected in Series Byrubber Bushing of Big Stiffness
5 讨论与结论
通过对包含串联节点刚度的隔振系统的传递率特性进行理论分析及实验验证,得到以下主要结论:
(1)推导出系统上层质量和节点的位移响应计算公式,其数值上相差,并得到了系统传递率计算公式。
(2)对于质量和隔振器刚度、阻尼均确定的系统,在共振区附近,随串联节点刚度增大,传递率明显下降,串联刚度大于一定值后,传递率趋于稳定。
(3)对于质量和隔振器刚度、阻尼均确定的系统,在过共振区,随串联节点刚度减小,传递率明显下降,串联刚度小于一定值后,传递率趋于稳定。
(4)实验验证了在过共振区,减振器串联不同节点刚度对传递力的影响规律,理论和仿真分析与实验吻合良好,对端部采用变刚度节点减振器的设计具有重要的参考意义。
