基于时频分析法的地磁数据研究

王 静，贺 巍，汪伟明

（陕西省地震局 榆林综合地震台，陕西 西安 710068）

0 引 言

目前，我国的地震前兆观测主要有地下流体观测、形变观测和地磁观测3种手段[1]。其中，地磁观测是基于地球主磁场及其长期变化、岩石磁学和古地磁学、地磁场起源的研究。

榆林综合地震台的地磁相对观测系统采用GM4型磁通门磁力仪，主要是对磁偏角D、水平强度H和垂直强度Z三要素的测量。磁通门磁力仪记录的是秒数据，地磁观测数据易受地球磁场、观测场地环境和观测设备故障等因素的影响，导致观测数据出现台阶、突跳、毛刺和缺数现象，而这些干扰和噪音都属于随机信号范畴。时频分析法是针对时域和频域联合的分布信息，主要分析信号频率随时间变化的关系。文中通过使用短时傅里叶变换和小波变换两种时频分析方法对地磁数据进行对比分析研究。

1 短时傅里叶变换变换

短时傅里叶变换（Short Time Fourier Transform，STFT）通过选择一个时频局部化的窗函数，通过移动窗函数计算各个不同时刻的功率谱。窗的长度决定频谱图的时间分辨率和频率分辨率。窗长越长，截取的信号越长，傅里叶变换后频率分辨率越高，时间分辨率越差。但是，为了获得信号的平稳性，需要一个较短的窗函数。在短时间内信号是平稳的，时间分辨率越高，频率分辨率越低。使用短时傅里叶变换不能兼顾时间分辨率和频率分辨率，应根据具体需求进行选择。

离散时间信号x(n)的短时傅里叶变换定义为[2]：

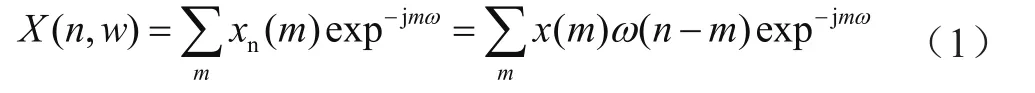
其中，ω(n)是窗函数，窗的长度为Nω。选择中心对称的滑动窗，能量集中在m或者原点（m=0）附近。

2 小波变换

受塔式算法的影响，1989年Mallat提出了著名的Mallat算法，可以快速实现信号的塔式多分辨率分析分解与重构。小波变换是原始信号与经过伸缩后的小波函数族的相关运算，通过尺度伸缩和平移等运算实现对信号进行多尺度细化分析。原始信号进行滤波后，高通滤波器输出信号的高频部分，而高频成分具有信号的细节或差别。低通滤波器输出信号的低频部分，低频成分蕴含着信号的近似特征。小波变换能较好地解决时间和频率分辨率的矛盾[3]：小波变换的窗是可调时频窗，在高频时使用短窗口，在低频时则用宽窗口，以不同的尺度观察信号，以不同的分辨力分析信号。

离散小波变换（Discrete Wavelet Transform，DWT）是对连续小波变换的尺度、位移按照2的幂次进行离散化得到的，也称之为二进制小波变换。取小波变换的尺度伸缩参数a=a0m，小波变换的平移参数b=nb0a0m，一维离散小波函数可表示为[4]：

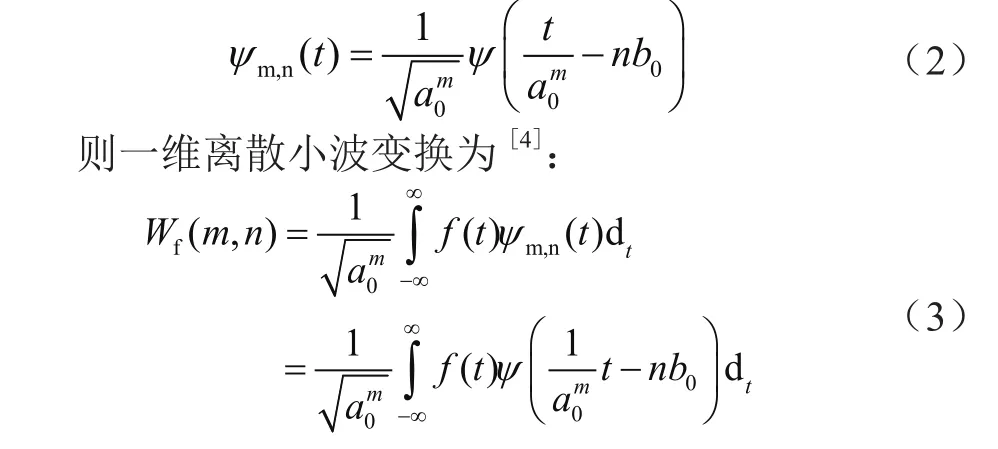
3 计算结果与分析

分析榆林台GM4型磁通门磁力仪GM4-1的地磁秒数据，选择2019年01月02日榆林台GM4-1受高压直流干扰数据作为实验数据，上临线日00:31至11:09时Z分量累计变幅16.2 nT，9:35至9:39变幅6.1 nT。

3.1 地磁秒数据的短时傅里叶变换结果

对地磁秒数据进行傅里叶变换，结果如图1所示。图1（a）为地磁秒数据的时间域曲线图，图1（b）为地磁数据H分量在频率域的Fourier变换，地磁数据集中在低频段。对地磁秒数据进行短时傅里叶变换，选择长度为41的hamming窗，得到图1（c）的时频平面分布的能量谱图，图1（d）则是地磁秒数据短时傅里叶变换的时频分布的立体表示。可见，短时傅里叶变换不仅能看出频率的分布区间，还能看出频率随时间的变化。

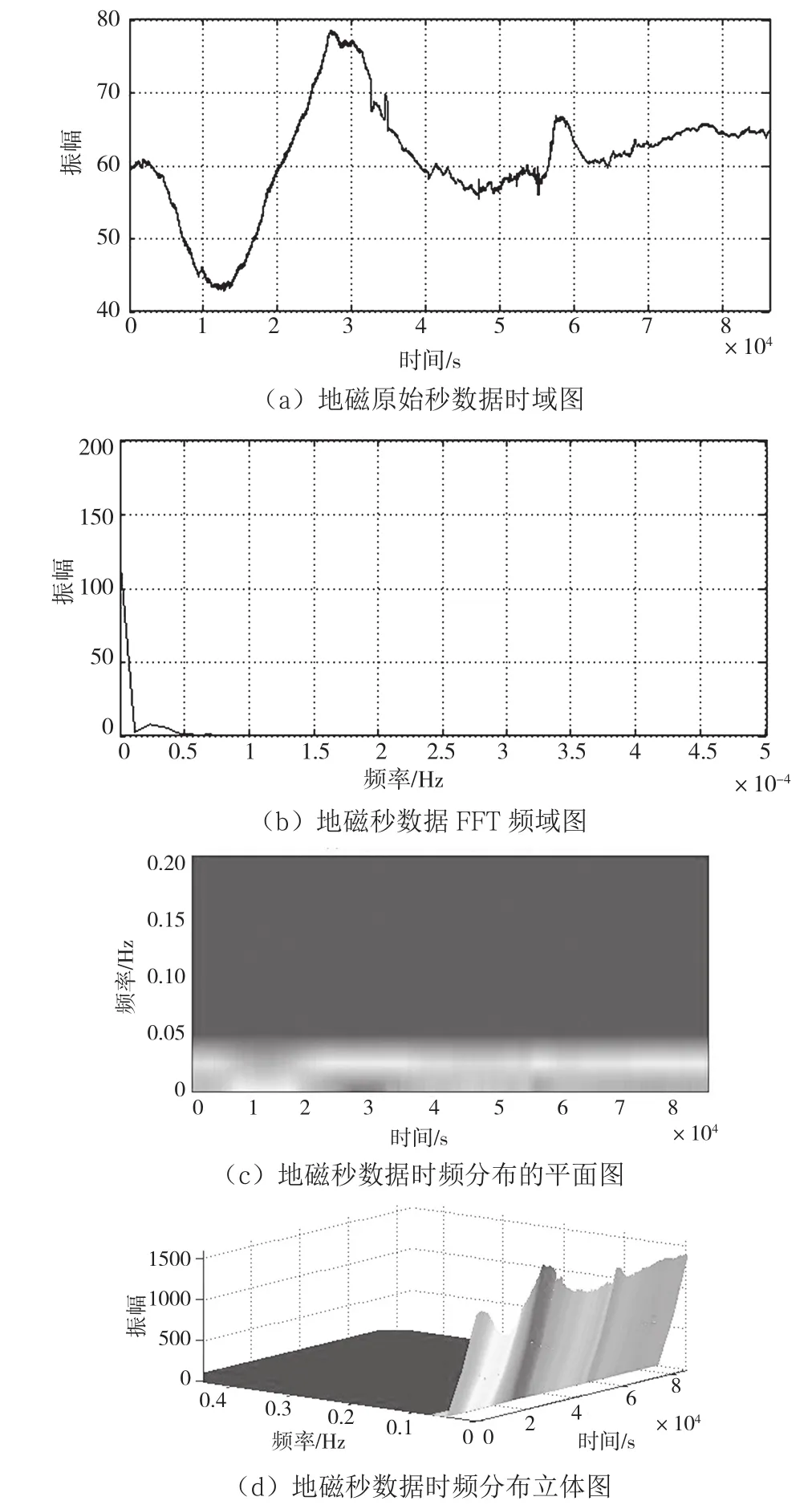
图1 原始数据及其对应的短时Fourier变换谱图

3.2 地磁秒数据的小波变换结果

对榆林台地磁秒数据进行小波变换，结果如图2所示。其中，图2（a）为地磁数据的时间域曲线图，图2（b）为地磁数据的一层小波分解的低频信息，与原始信号的特征相似。图2（c）为地磁数据的一层小波分解的高频信息，具有原始信号的细节或差别，可看出信号整体受噪声干扰，在高直干扰时段台阶波形明显。图2（d）是地磁数据原始经过一层小波分解后的重构信号，滤除了部分噪声。

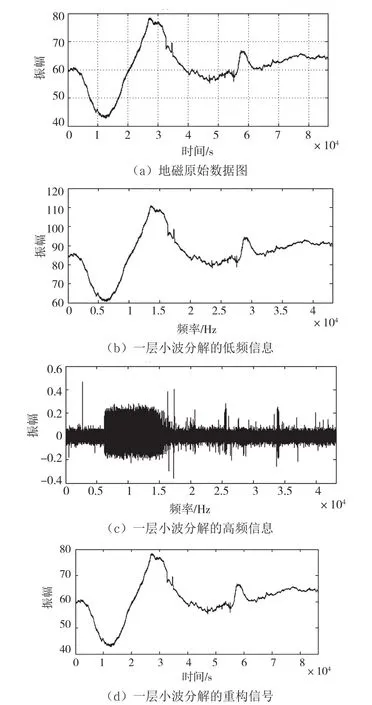
图2 原始秒数据及其对应的小波变换

4 结 论

本文采用短时傅里叶变换和小波变换对地磁数据进行分析研究。使用短时傅里叶变换不仅可以知道频率分布，还可以知道在哪个时间点上出现了什么频率但是无法使时间分辨率和频率分辨率最优。小波变换可以在高频分量采用高的时间分辨率和低的频率分辨率，在低频分量采用高的频率分辨率和低的时间分辨率，这种多分辨分析方法对于地磁信号有很好的分析效果。