基于MAYR电弧模型的船舶直流配电系统熔断器仿真研究

兰 喆，胡伟毅

（1.武汉理工大学，湖北 武汉 430070；2.国网荆州供电公司，湖北 荆州 434000）

0 引 言

现阶段，传统柴油机船舶尾气污染已经成为第三大大气污染来源。随着蓄电池储能和快速充电技术的不断革新，无噪声零排放的新能源电动船舶得到了巨大发展[1]。但是，大量变频器、逆变器以及储能等设备的加入，给船舶直流配电系统的安全性和可靠性带来了挑战。

熔断器是直流微电网保护中的重要组成器件[2-4]。熔断器的核心部件为熔体。正常工况下，熔体温度保持稳定，不会熔断；发生短路故障时，流经熔体的电流过大致使熔体温度不断上升，直至熔体熔断。熔体熔断后，断点两端高压高温会在间隙产生电弧。只要有电弧存在，电路中的电流就无法完全切断。只有电弧完全熄灭后，电路中短路电流才能为零[5]。因此，有必要分析熔断器电弧特性，为熔断器的容量选型提供依据。

国内外对电弧的研究方法基本分为仿真法、理论计算法和现场实测法3类。由于理论计算法无法准确描述短路电流和短路电压随时间的变化趋势，而现场实测法代价高昂且有一定的危险性，因此多采用仿真法研究电弧。

通常在进行仿真保护验证时，为评估熔断器开断能力和其开断时对电流的影响，需要在理想模型中加入电弧模型[6]。电弧模型的本质是用阻抗模型近似等效电弧故障。对电弧的宏观描述通常有Mayr模型、Cassic模型和Ayrton模型等[7-8]。由于Ayrton模型不能体现电压和电流的暂态特性标准，而Cassic模型关于电弧电压为常数的假设前提无法描述电弧电阻继续增长的实际情况，因此本文选用Mayr模型对故障电弧进行准确描述。

本文基于船舶直流配电系统短路故障的应用场景，使用基于MAYR电弧模型的熔断器，在MATLAB/SIMULINK平台上设计、搭建仿真系统，并进行短路故障仿真以验证其保护效果。最后，通过在实际平台上开展短路故障仿真，验证了此熔断器设计能在船舶直流微电网出现短路故障时有效保护变换器等关键部件。

1 系统拓扑图

系统仿真拓扑图如图1所示。

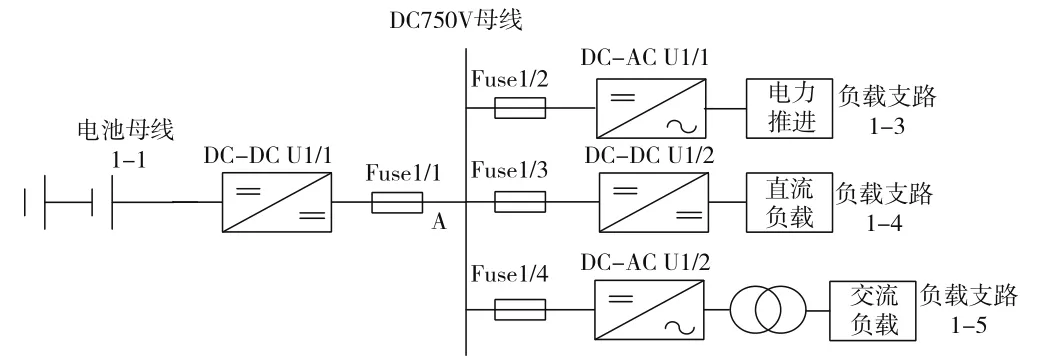
图1 系统仿真拓扑图

系统中，锂电池电压为565 V，经过DC-DC变换器U1/1升压至750 V。船用负载分为推进负载、释能负载和交流负载。当DC-DC变换器U1/1出口侧发生短路故障即图1直流母线上端A点发生短路故障时，短路点电流由U1/1输出电流和负载支路储能元件馈送短路电流组成，即：

式中，ID是经A点接地的短路电流，I1是DC-DC变换器U1/1输送的短路电流，I2是DC-AC变换器U1/1输送的短路电流，I3是DC-DC变换器U1/2输送的短路电流，I4是DC-AC变换器U1/2输送的短路电流。

由于故障瞬间直流母线电压断崖式跌落，负载支路变换器停止工作，电池母线输出电流成为短路电流最主要的组成部分。因此，在短路故障仿真中，重点对图1中FUSE1/1熔断器的性能进行考察。

对仿真模型进行简化，将3条负载支路阻抗分别等效为Z1-3=3.75 Ω、Z1-4=30.4 Ω和Z1-5=10.75 Ω。

2 基于Mayr电弧模型的熔断器模型

熔断器的动作靠熔体的熔断来实现，因此其最明显的特性是安秒特性。熔体的安秒特性可以从焦耳定律理解。焦耳定律方程为：

式中，Q、I、R、t分别为熔体吸收热量、流过熔体的电流、熔体电阻、熔体受热的时间。由式（2）可知，熔体吸收热量Q与电流I的平方成正比，与受热时间t成正比。

熔断器的熔断过程包含熔化、汽化和电弧3个主要过程。电弧本质上是一种等离子通道，因此对电弧电阻的直接测量存在极大困难。为了准确描述熔断器的熔断状态，需要用数学模型准确描述熔断器各阶段的阻值变化。

2.1 电弧模型数学基础

在电弧模型研究初期，多数人认为可以把电弧通道理解为可变电阻，电弧特性可以通过非线性微分方程表示。如果把电弧看作圆柱形的气体通道，就可以依据能量守恒定律写出电弧电导随能量变化的函数关系式，得到电弧的数学模型。

电弧能量的变化过程决定了电弧电阻Ra的变化过程，一般可表示为[9]：

式中，ia是电弧电流的瞬时值，E是弧柱电压梯度的瞬时值，Ra是单位长度电弧电阻的瞬时值，P是单位长度电弧的输入功率，Po单位长度电弧的散出功率，t是时间。

电弧能量与电弧电阻的数学关系还可以描述为：

式中，Q是单位长度中电弧累积的能量。Q与t之间的关系可表示为：

式（5）对t进行微分计算，得：

2.2 Mayr电弧数学模型

Mayr电弧模型有以下假设前提：（1）弧柱是一个圆柱体；（2）能量是依靠热传导和径向扩散作用散出的，即散热功率是一个常数；（3）忽略电弧柱中气体的热物理性质随温度的变化而变化；（4）附注中热游离情况由热游离哈沙公式确定。

在Mayr模型假设成立的前提条件下，可得：

式中，g、k、Q、Qo分别为电弧电导、常数、单位长度中电弧积累的能量、电弧电导g变化e=2.718倍时所需要的能量。

对式（7）等号左右两边同时对时间求一阶积分，得：将式（8）带入式（6），得到模拟电流过零时的电导变化方程式为：

式中，ϑ=Qo/PoM为电弧的时间常数[10-15]，PoM是静态功率损失。

2.3 基于Mayr电弧模型熔断器仿真模型

以MATLAB软件为平台，使用Simulink中的元件建立Mayr电弧模型熔断器仿真模型。模型由电压控制电流源、微分方程编辑器、定制检测、阶跃信号以及电压测量等模块构成。电弧模型的微分方程可采用Simulink中的微分方程编辑器（DEE）模块实现。Mayr电弧模型的微分方程为：

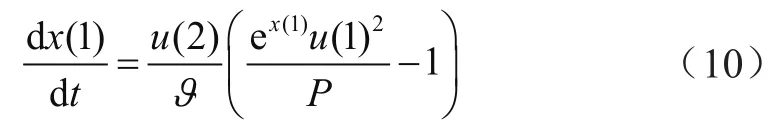
式中，x(1)是微分方程状态变量，即电弧电导的自然对数ln g；x(0)是状态变量的初始值，是电弧电导的初始值g(0)；u(1)是DEE第一个输入量，即电弧电压u；u(2)是DEE的第二个输入量，表示断路器触头的关合状态（当触头闭合时，u(2)=0；当触头断开时，u(2)=1）；ϑ是电弧时间常数；P是（静态功率损失）电弧散热功率。ϑ和P是Mayr电弧模型的自由参数，可在Mayr电弧模型的对话框中进行设置和更改。

仿真模型中用阶跃信号模拟控制断路器触头的分离。

当触头闭合时，即：

此时，电弧模型以电导的形式表示即为g(0)。

当触头分离时，电弧模型表示为式（10），其中电弧电导和断路器分断时间都能在模型设置中任意设定。

3 系统短路故障仿真

3.1 基于Mayr电弧模型熔断器的系统故障仿真

通过查阅文献资料、产品参数表及实际实验数据归算，Mayr电弧模型熔断器电弧时间参数、初始电导、散耗功率和触头分断时间分别设置为0.3×10-6s、1×106S、5×106W 和 1.4×10-4s。

仿真模型采用初始电压值为750 V的电容替代电池，以模拟短路故障时刻前系统正常工况，即0时刻起，仿真系统A点处发生短路故障，仿真时间0.04 s。由参数设置可知，140 s后，熔断器完成熔断动作，切除系统短路故障。熔断器两端电压波形如图2所示，通过熔断器的电流波形如图3所示。

图2 熔断器两端电压波形

图3 通过熔断器电流波形

由图2可知，熔断器电压在1.40×10-4s时刻之前始终为0，此时熔断器熔体并未熔断，温度不断上升；熔断器在1.40×10-4s时刻至1.48×10-4s时刻，两端电压由0 V逐渐上升；在1.48×10-4s时刻之后，熔断器两端电压稳定在591.3 V。

由图3可知，由于仿真系统在0 s时刻即发生短路故障，因此流过熔断器的电流在0 s时刻为最大值2.616×105A；在0 s时刻至1.40×10-4s时刻，由于大电流从熔体流过，熔体温度上升，熔断过程中电阻值升高，流过熔断器的电流呈下降趋势；在1.40×10-4s时刻熔断器触头分断，故障电弧出现，电流急剧减小；1.56×10-4s时刻之后，熔断器电弧熄灭，电路电流为0 A。

综上所述，熔断器在1.56×10-4s时刻完成熔断动作，即熔断器在短路故障发生后156 μs完成熔断动作，电路发生短路故障时能实现对上下级器件的有效保护。

3.2 实验结果

实验现场如图4所示。在实柜实验中，同样使用充电至750 V电容替代电池，以模拟短路故障时刻前的系统正常工况。实验测试波形如图5所示。

图4 实验现场

图5 实验测试波形

实验中，示波器1号通道测量直流母线的电压，2号通道使用有源探头测量图1中A点发生短路故障时通过熔断器的电流，探头放大比例为100:1。

由图5可知，短路故障发生时，直流母线电压由750 V开始下降直至稳定在590 V左右，即熔断器两端电压稳定值为590 V；短路点短路电流峰值为25.6 kA；熔断器熔断时间约为140 μs。

仿真结果与实验结果计算可知，熔断器两端电压误差为：

4 结 论

本文针对船舶电力系统应用环境，提出了应用Mayr电弧模型熔断器对直流系统进行短路故障仿真实验。由仿真结果与试验结果对比可知，基于MAYR模型熔断器在仿真中能较好地复现短路故障发生时熔断器的两端电压、流过熔断器电流的峰值、稳定值和变化趋势，误差在3%以内。

由于Mayr模型建立过程中引入了电弧电压、电弧电流以及静态功率损失等电弧内部参数，且模型利用更精确的数学模型对电弧电阻变化过程进行描述，因此运用该模型可以在实验条件受限的情况下开展故障电弧研究，为后续实验平台熔断器的选型提供可靠的依据。