基于卡尔曼滤波算法的上证50指数预测

梁　伟

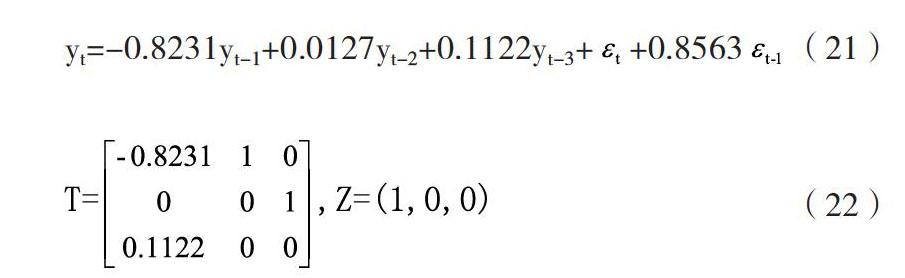
摘要： 本文基于ARMA模型构建卡尔曼滤波算法的线性状态空间模型，然后利用ARMA模型的卡尔曼滤波算法来预测上证50指数，并且将预测结果与基于ARMA模型的预测结果进行了比较，结果表明，结合了ARMA模型的卡尔曼滤波算法的预测准确度为52.1%，明显优于单纯的ARMA模型。

关键词： ARMA模型 卡尔曼滤波算法 预测

一、引言

金融时间序列分析一直是学术界的研究热点，同时各类数学模型及机器算法也在不断地发展和优化，ARMA模型及卡尔曼滤波算法都是非常有效的金融时间序列分析方法，本文将二者相结合使用以提高指数预测的准确度，具有一定的学术意义及现实可操作性。

在国外，卡尔曼（Kalman）和布塞（Bucy）在1960年发表了一篇名为《线性滤波和预测理论的新成果》的论文，提出了一种新的线性滤波和预测理论，被称之为卡尔曼滤波。在国内，彭继兵和唐春艳（2005）基于变维分形理论的卡尔曼滤波算法对股票价格进行了预测，结果发现基于变维分形理论的卡尔曼滤波动算法对股价的预测是有效的。刘向阳（2019）对几种典型非线性滤波算法及其性能进行了分析，文章通过仿真实验对四类滤波器性能进行了对比分析，研究结果表明，EKF 计算量小，PF 精度高，UKF和CKF具有较高的精度和较强的实时性。

二、卡尔曼滤波算法

（一）算法概念

卡尔曼滤波算法是一个最优化自回归数据处理算法，该算法由状态方程和观测方程组成的线性随机系统的状态空间模型来描述。该算法利用状态方程的传递性，按线性无偏最小均方误差估计准则，利用新观测数据，对系统状态变量作最佳估计。具体来讲，状态方程负责向前推算当前状态变量和误差协方差的估计值，为下一个时间状态构造先验估计。测量方程负责反馈，即将先验估计和测量变量结合以构造后验估计。卡尔曼滤波算法的这些特性非常适合用于金融时间序列短期预测，下面即为卡尔曼滤波算法进行金融时间序列短期预测对应的运行流程，如下：

系统状态：X（k）=AX（k-1）+BU（K）+W（K）（1）

系统预测值：Z（k）=HX（k）+V（k）（2）

上面公式1、2即为卡尔曼滤波算法的线性状态空间模型，其中X（k）是k时刻的系统状态，U（K）是k时刻对系统的控制量，它可以为0。A和B是参数，对于多模型系统，它们是矩阵。Z（k）是k时刻的测量值。H是测量系统的参数，对于多测量系统，H为矩阵。W（k）和V（k）分别是系统状态和测量值的噪声。

假设现在的系统时刻是k，过程模型利用上一时刻的系统状态预测现在的系统状态：

X（k|k-1）=AX（K-1|K-1）+BU（k）（3）

在上式中，X（k|k-1）是k时刻的系统状态预测结果，X（K-1|K-1）是（k-1）时刻系统状态的最佳估计值。系统状态已经更新，接下来更新X（k|k-1）对应的协方差，我们用P表示协方差，如下：

P（k|k-1）=AP（k-1|k-1）AT+Q（4）

在上式中，P（k|k-1）是X（k|k-1）对应的协方差，P（k-1|k-1）是X（k-1|k-1）对应的协方差，AT为A的转置矩阵，Q是系统过程的协方差。

现在我们利用系统状态的预测值及观测值估计系统状态的最优值X（k|k），如下：

X（k|k）=X（k|k-1）+Kg（k）[Z（k）-HX（k|K-1）]

（5）

在上式中，Kg（k）为卡尔曼增益：Kg（k）=P（k|k-1）HT/[HP（K|K-1）HT+R]（6）

现在我们已经得到了k时刻系统状态的最有估计值X（k|k），但是为了让系统继续运行下去，我们还需要更新k时刻系统状态X（k|k）对应的协方差，如下：

P（k|k）=[1-Kg（k）H]P（k|k-1）（7）

以上便是进行短期价格预测的卡尔曼滤波算法的自回归运算过程。

（二）算法应用

卡尔曼滤波算法是目前应用最为广泛的滤波方法，在导航、控制及金融数据分析等领域都取得了较好的应用效果。卡尔曼滤波算法对系统状态的估计可以是对当前系统状态的估计（滤波），也可以是对于将来系统状态的估计（预测），也可以是对过去系统状态的估计（插值或平滑）。卡尔曼滤波算法对金融时间序列短期预测属于对未来系统状态的估计，通常通过MATLAB、Python及R语言来实现。以MATLAB为例，在利用卡尔曼滤波算法进行高频交易的时候，投资者将高频价格信息输入卡尔曼滤波函数，就可以预测短期价格指数。

三、ARMA模型

（一）模型概念

自回归移动平均模型（ARMA模型）由因变量对它的滞后值以及随机误差项的现值和滞后值回归得到，该模型具体可分为移动平均（MA）模型、自回归（AR）模型及自回归移动平均模型。

1.MA（q）过程的表示形式：

（8）

在上式中，c为常数项，{}为白噪音过程。对于任意的t，MA（q）都是平稳的。

2.AR（p）过程的表示形式：

（9）

在上式中，c为常数项，{}为白噪音过程。当特征方程的根全部落在单位圆之外时AR（p）过程是平稳的。

3.ARMA过程的表现形式：

（10）

在上式中，{}为白噪音过程。ARMA过程的稳定性取决于它的自回归过程。

引入滯后算子L，上式可以写成：（11）

其中，;。

（二）模型应用

1.ARMA模型的识别。利用自相关函数（ACF）及偏自相关系数（PACF）识别ARMA模型，具体步骤为：第一步，通过ADF检验判断时间序列的平稳性;第二步，利用ACF、PACF及它们的图形来确定ARMA（p，q）模型的参数p、q。

2.ARMA模型的诊断与检验。具体步骤为：第一步，通过t检验检验模型参数的显著性;第二步，通过Q统计量检验残差序列的随机性。

四、基于ARMA模型的线性状态空间模型的建立

基于ARMA模型建立卡尔曼滤波算法的线性状态空间模型，即将ARMA模型转化为状态空间模型，本文利用Harvey方法进行模型转化。

考虑上面均值为0的ARMA（p，q）过程yt：

令m=max（p，q+1）且将上式改写为：（12）

在上式中，，，并且（因为m>q）。

现在我们将上面提到的卡尔曼滤波算法所对应的状态空间模型（公式1、2）转变为广义高斯线性状态空间模型，如下：

状态方程：（13）

观测方程：（14）

在上式中，是m维状态向量，是k维观测向量，dt和ct分别是m维和k维的确定性变量，Tt和Zt分别是m×m和k×m的系数矩阵，Rt是m×n矩阵，且{}和{et}分别是n维和k维高斯白噪声序列。

Harvey给出了具有m维状态向量st的状态空间的一种形式，该状态向量的第一个元素是yt，即s1t=yt，st的其它元素通过递归得到，由ARMA（m，m-1）模型可以求出：

（15）

其中，且如前述定义，考虑可以得到：（16）

重复上述过程，可得：（17）

进一步可得：（18）

将上述方程综合起来，可以得到如下状态空间模型：

（19）

（20）

以上即为基于ARMA模型建立卡尔曼滤波算法对应状态空间模型的具体过程。

五、上证50指数预测

（一）数据选取

选取上证50指数日收盘价数据，时间区间为2018年1月2日到2019年8月30日，一共406个数据，然后计算日收盘价的对数收益率序列（日收益率），计算公式为：yt=ln（Pt/Pt-1），公式中Pt表示上证50指数第t日收盘价，Pt-1表示第t-1日收盘价，一共得到405个对数收益率数据。

（二）基于结合了ARMA模型的卡尔曼滤波算法的指数预测

本文通过Python3.0平台进行基于卡尔曼滤波算法的上证50指数预测，首先获取指数日收盘价、对数收益率（日收益率序列），然后建立收益率序列的ARMA模型。aic-order与hqic-order均给出AR过程阶数为3，MA过程阶数为1，符合前面假设：p >= q+1，故令order = （3，1）。通过ljung-box检验，判断ARMA（3，1）模型残差序列是否存在滞后相关，检验结果表明滞后40阶以内的p-value均大于0.05，故可以判斷残差中没有显著的序列相关性，接下来进行模型的转化。

通过Harvey方法实现ARMA模型向拉尔曼滤波算法状态空间模型的转化部，可得：

yt=-0.8231yt-1+0.0127yt-2+0.1122yt-3++0.8563（21）

（22）

接下来运行基于ARMA模型的卡尔曼滤波算法，上证50指数预测结果与真实值如下图：

图1 上证50指数卡尔曼滤波算法短期预测图

进一步计算卡尔曼滤波算法预测的准确度为0.5210。

（三）基于ARMA模型的指数预测

单纯基于ARMA模型的上证50指数预测结果如下图：

图2 上证50指数ARMA模型预测图

基于ARMA模型的上证50指数预测准确度为0.4687。

六、结论

由上面预测结果可知，相比于ARMA模型的预测结果，结合了ARMA模型的卡尔曼滤波算法在上证50指数的预测中，其预测的准确度高于单纯的ARMA模型，准确度提高了5.2%。说明卡尔曼滤波算法经过与ARMA模型的结合，对于噪声过滤效果更好。不过，结合了ARMA模型的卡尔曼滤波算法相对其它机器算法及数学模型，预测的准确度还不够高，仍然存在较大的优化空间。

参考文献：

[1]Kalman R E，Bucy R S.New Results in Linear and Prediction Theory.Trans ASME，J  Basic Eng，1961;83：95-107.

[2]彭继兵，唐春艳.基于变维分形理论的卡尔曼滤波实时跟踪预测模型在股票价格预测中的应用[J].机算机工程与应用，2005（13）：218-223.

[3] 刘向阳.几种典型非线性滤波算法及性能分析[J].舰船电子工程，2019（7）：32-35.

作者系山西财经大学金融学院金融专业2018级硕士研究生