改进双边滤波和阈值函数的图像增强算法

常 戬，贺春泽，董育理，任 营

辽宁工程技术大学 软件学院，辽宁 葫芦岛125105

1 引言

图像在获取和传输的过程中，由于受外界环境因素和设备的影响，质量有所下降。图像增强现已广泛地应用到某些特定领域。通过图像增强的方法丰富图像的细节信息，改善图像视觉效果，对后续的医学研究、遥感图像、机器识别等领域有重大的意义。

图像增强的传统方法有直方图均衡化法、基于人类视觉的Retinex算法、反锐化掩膜法、线性变换法。直方图均衡化方法提升图像的对比度，简单高效，处理速度快，但对有效信息无法做到针对处理，易造成局部过增强[1]；20世纪70年代，Land首次提出Retinex理论[2]，Retinex算法保持色彩恒常性，消除了光照环境对图像本质的影响，文献[3]中Jobson等人提出单尺度Retinex算法，但其算法在图像光照不均匀处容易产生光晕现象。文献[4]中胡韦伟等人提出基于双边滤波的Retinex算法，去除了光晕现象，但同时造成了图像泛灰；文献[5]中张雪峰等人提出一种I-Retinex算法在去除光晕现象的同时去除图像噪声，丰富了图像细节，但依然存在泛灰现象。反锐化掩膜法通过加强图像的边缘、轮廓等高频信息增强图像细节，但增强后图像的边缘处仍存在光晕现象，且光照平缓的区域增强幅度较小[6～7]，线性变换法可以通过设置不同的斜率，增强图像对比度，但针对不同灰度图像需要做不同处理，且在灰度值较大区域易产生过增强现象。20世纪90年代，Donoho[8]提出了基于频率域的软阈值函数和硬阈值函数去噪方法并同时证明了相比传统去噪方法的优越性[9]，该方法计算量小、易实现，但软阈值方法在高频系数大于固定阈值时会产生恒定误差，造成边缘细节模糊，硬阈值方法解决了软阈值方法的恒定误差问题但在间断点处不连续，易产生震荡现象。

针对上述算法存在的不足，在小波变换的基础上，针对低频和高频系数分别提出改进双边滤波的Retinex图像增强算法和改进阈值去噪算法。克服了上述算法存在的光晕现象、图像模糊、细节丢失和泛灰等现象，并有效地去除了噪声。

2 本文算法

本文用小波变换的方法将图像增强和图像去噪的思想相结合。首先对含噪图像进行小波分解，得到分解后的低频和高频系数；对低频系数采用改进双边滤波的Retinex图像增强算法，对高频系数采用改进阈值函数方法进行去噪；然后对处理后的低高频系数进行小波反变换，得到重构图像；最后采用分段性线性变换方法对重构图像进行对比度增强，有效解决了图像因对比度不足的泛灰现象。本文算法具体步骤如下：

（1）对含噪图像进行小波分解，得到低频系数和高频系数。

（2）采用改进双边滤波的Retinex图像增强算法对低频系数进行处理。

（3）采用改进阈值函数方法对高频系数进行处理。

（4）对处理后的低频和高频系数进行小波重构，得到重构图像。

（5）对重构后的图像进行分段性线性变换处理，得到增强图像。

本文算法具体流程图如图1所示。

2.1 小波分解与重构

本文采用小波变换的方法将含噪图像分解为低频系数和高频系数。其中低频系数主要包含图像的全局信息，包括图像的轮廓信息，而高频系数主要包含图像的局部信息，包括图像的边缘、细节、噪声部分。二维离散小波分解公式如下：

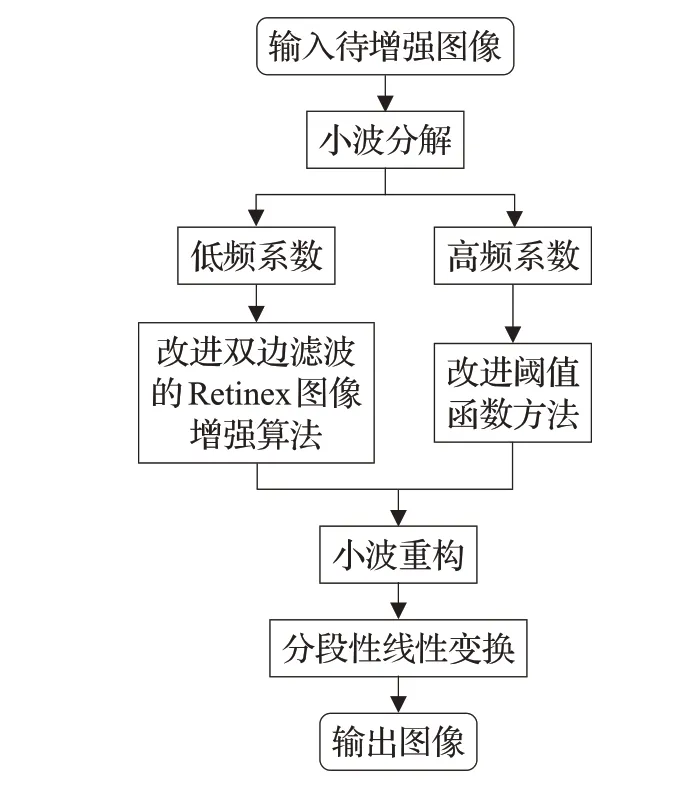
图1 本文算法流程图

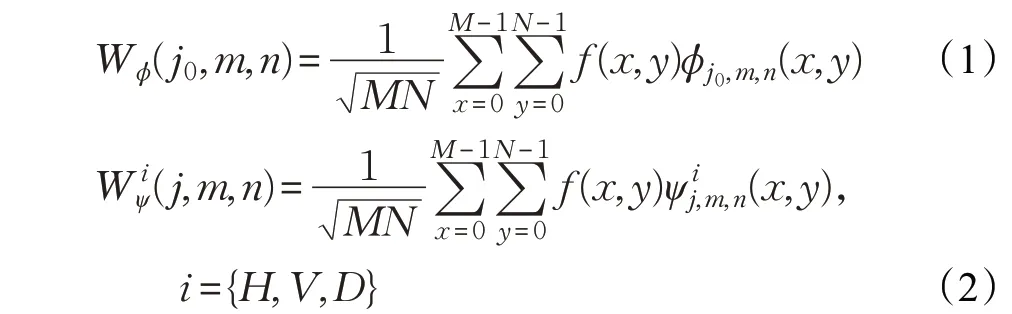
其中，Wφ(j0,m,n)为分解后低频系数，为分解后高频系数，表示为H、V、D，j0是一个任意开始尺度，通常令其为0，f(x,y)为离散函数，x和y表示离散变量；m，n表示为相对(x,y)的相对偏移量，M与N代表图像由M×N个像素组成φj0,m,n(x,y)为二维尺度函数，为i所对应的水平、垂直、对角方向的小波函数。

结合分解后得到的低频系数Wφ(j0,m,n)和高频系数Wiψ(j,m,n)，并经过改进双边滤波的Retinex图像增强算法和改进阈值函数方法分别对低高频系数的处理，通过离散小波反变换得到重构后图像，小波重构公式如下：

2.2 改进双边滤波的Retinex算法

本文采用改进双边滤波的Retinex图像增强算法对图像经小波分解后的低频系数进行光照图像估计，有效避免了光晕现象。

Retinex理论是Land基于人类视觉感知模型提出的一种计算理论。由Retinex理论可知，人类观察到的图像是由光照图像和反射图像两部分组成即：

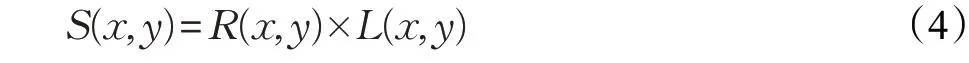
其中，S(x,y)为原始图像，R(x,y)为反射图像，L(x,y)为光照图像。光照图像反映了图像能达到的动态范围，包括光照强度和环境等信息，反射图像反映了图像纹理和轮廓等信息[10]。Retinex算法为使图像不受光照环境的影响，消除原始图像中的光照图像，经对数域转换后得到能反映图像本质的反射图像[11]。通过对单尺度Retinex算法及基于双边滤波Retinex算法的实验发现，若完全消除原图像中的光照估计部分，往往会出现图像不自然现象，因此在消除光照图像的过程中增加一个光照调节参数k(k∈(0,1))。反射图像公式如下：

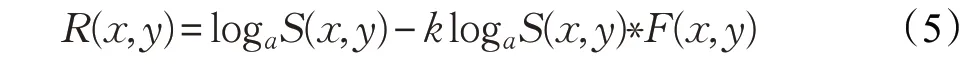
其中，k为光照调节参数，F(x,y)为高斯核函数，光照图像L(x,y)由原始图像与高斯核函数卷积得到。

基于双边滤波的Retinex算法针对单尺度算法产生的光晕现象进行改进，在考虑了像素值的欧式距离的同时还考虑了像素范围域中的辐射差异。双边滤波公式如下：

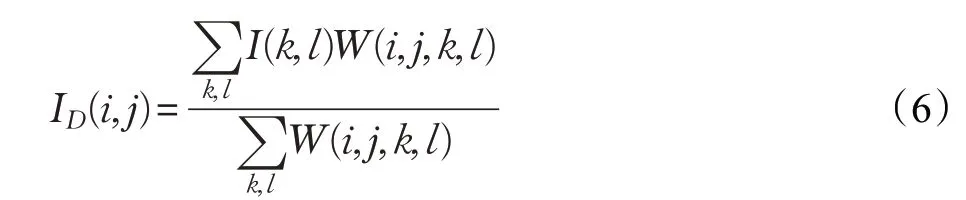
其中ID(i,j)为输出图像，I(k,l)为原始图像，W(i,j,k,l)是空间域与像素范围域的核函数。在图像像素值变化程度较小的平缓区域，双边滤波在空间域起主要在作用，此时相当于高斯滤波。在图像像素值变化程度较大的边缘区域，同时考虑空间域和像素值域，在保持图像边缘信息的同时有效避免边缘处由图像亮度差异较大引起的光晕现象。双边滤波公式如下：

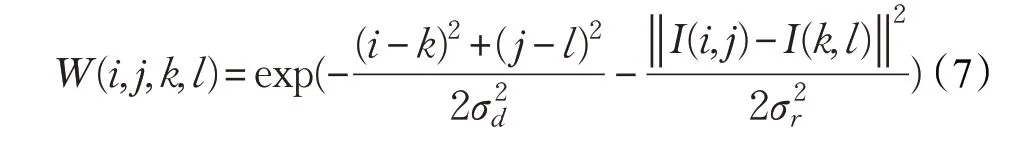
本文提出改进双边滤波的Retinex图像增强算法，针对双边滤波核函数中像素点的空间域进行改进，改进双边滤波公式如下：

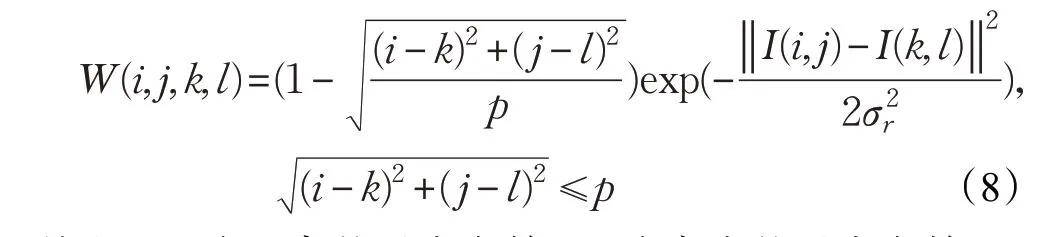
其中，σd为距离差尺度参数，σr为亮度差尺度参数，p为滤波窗口参数。

在空间域处，设置滤波窗口参数p，原双边滤波的滤波窗口大小为2p+1，改进双边滤波的滤波窗口为以滤波中心像素点为中心，以滤波参数p为半径的圆形区域。当滤波邻域内像素点与滤波中心像素点距离小于滤波窗口参数时，判断该像素点位置在半径范围内，则该像素点空间域与像素值域同时生效，在平滑噪声的同时保持图像的边缘信息。当滤波邻域内像素点与滤波中心像素点距离大于滤波窗口参数时，认定该点距离中心像素点较远，对该像素点不作处理，以消除该像素点对图像边缘的影响。使用改进双边滤波算法得到的反射图像不仅有效地保持边缘细节，且更好地去除了光晕现象。

2.3 小波高频系数处理

本文采用改进阈值函数方法对小波分解后的高频系数进行去噪处理。在阈值函数处理前，为了分离高频系数中的噪声分量，首先需确定函数阈值，由于固定阈值估计法对噪声在高频系数处分布较多时有更彻底的去噪效果[12]。本文采用固定阈值估计法估计函数阈值，公式如下。

其中，T为确定的固定阈值，L·T为图像大小，σ为噪声标准方差，公式如下：

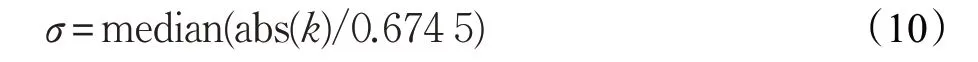
常见的传统阈值函数有硬阈值函数和软阈值函数。硬软阈值函数公式如下。

硬阈值函数：

软阈值函数：

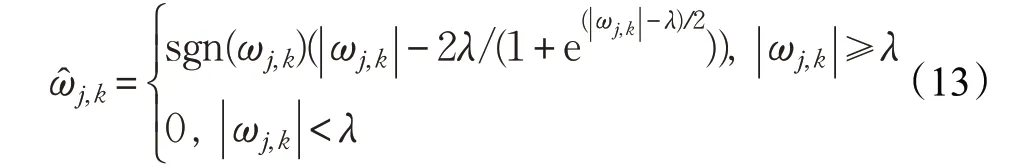
对比文献[14]提出的渐进半软阈值函数，针对硬、软阈值函数的不连续性和恒定偏差问题，本文提出一种改进阈值函数，公式如下：

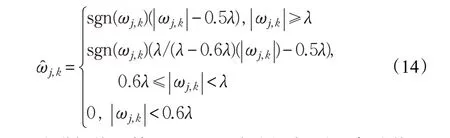
改进阈值函数以λ，0.6λ为分界点，分三部分估计高频小波系数。当高频系数大于固定阈值时，估计的高频系数为高频系数与固定阈值一半的差，相对软阈值函数，改进阈值函数减小了高频系数大于固定阈值时的恒定误差；高频系数介于0.6λ与λ之间时，通过式（14）有效提升高频系数；当高频系数小于0.6倍固定阈值时，将估计的高频系数置为0。与传统阈值函数相比，本文算法分三段处理，整体提高估计出的高频系数，更好分理出噪声分量，有效避免了震荡现象，并减少了阈值函数的恒定偏差。

本文采用改进双边滤波的Retinex算法对小波分解后的低频图像进行增强，采用改进阈值函数处理分解后的高频系数，再通过小波逆变换得到重构图像，如图2所示，图2（a）为含少量噪声图像，图2（b）为重构图像。

图2 含噪图像及重构后图像对比

2.4 对比度增强

在采用改进双边滤波的Retinex算法对低频系数处理和改进阈值函数对高频系数去噪后，重构后的图像存在泛灰现象，本文采用三段分段性线性变换[15]的方法提升图像对比度。三段分段性线性变换公式如下：

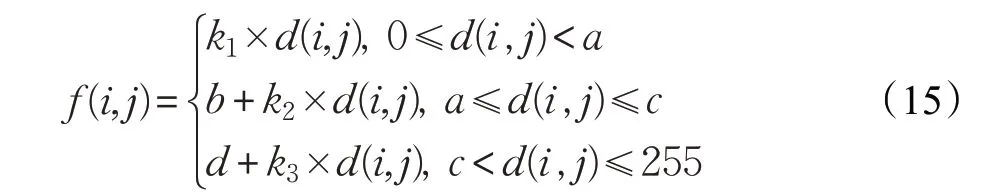
其中，f(i,j)为对比度增强后的输出图像，d(i,j)为输入图像，k1，k2，k3表示三段变换的斜率，其表达式如下：

其中(a,b)，(c,d)表示分段函数斜率发生变化的点。

分段性线性变换用法灵活，可根据不同特征图像的需要设置不同分段点，增强感兴趣区域细节，也可抑制不感兴趣区域。图3所示为分段性变换前后图像直观对比及直方图分布情况，图3（a）为小波重构之后图像，对比图2（a）可以看到使用改进双边滤波的Retinex算法后图像得到整体增强，但两侧墙壁、地面与中间门框处存在泛灰现象，对比度下降。因而本文将灰度值在[0，255]范围的图像以3/8，3/4为节点划分为三段，[0，3×255/8]对应图像较暗区域，[3×255/8，3×255/4]对应图像灰度值居中区域，[3×255/4，255]对应图像较亮区域。为增强对比度，同时避免对较亮区域压缩后产生的过增强现象，本文选择对暗区域灰度值进行少量压缩，对中间区域灰度值进行拉伸，较亮区域灰度值保持不变。

图3 分段性变换前后图像及直方图对比

对比图3（a）与图3（c），分段性变换前，图像中间处较亮的门框区域对比度较好，两侧墙壁与地面泛灰，分段性变换后，中间处亮区域对比度不变，整体对比度得到较好增强。对比图3（b）与图3（d），分段性变换前图像灰度值主要集中在[100，150]之间，分段性变换之后，较暗区域像素分布增加，相对均匀的分布在整个灰度之间。分段性线性变换增强了图像对比度，有效改善图像重构后的泛灰现象。

3 实验结果及分析

本文将图像增强和去噪的思想相结合，为了验证本文算法的有效性，从图像增强和去噪角度分别对实验结果进行分析。对添加了少量高斯白噪声的图像进行仿真实验。在验证本文去噪算法的有效性时，对小波分解后的高频系数分别采用软阈值函数、硬阈值函数、文献[14]阈值函数及本文改进阈值函数处理后进行对比，对小波分解后低频系数全部采用本文改进双边滤波的Retinex算法。在验证本文增强算法有效性时，将本文算法实验结果分别与单尺度Retinex（SSR）算法和基于双边滤波Retinex（BSSR）算法相比较。并采用主观视觉观察和客观数据分析的方法对上述算法从增强和去噪的角度进行对比评估。

实验平台为Windows8.1，MATLAB R2016a，Code：Blocks IDE。本实验中，低频系数采用改进双边滤波的Retinex算法估计光照图像，窗口参数为：p=3（滤波窗口大小为7），光照图像调节参数k=0.5，亮度差尺度参数σr=0.001，对高频系数采用改进阈值函数方法，分解与重构的小波基函数为sym4。分段性线性变换参数为：a=3L/8,b=L/4,c=3L/4,d=3L/4(L=255)。

针对光照图像调节系数k的取值，通过分析式（5）及文献[16]可知，当k取值接近0时，式（5）未起到消除光照图像作用，得到的反射图像与原图像相近；当k取值接近1时，将光照估计部分完全从原图像中消除，会产生图像不自然现象。本文为保证在一定程度上消除光照图像的同时避免图像不自然现象，将光照图像调节系数k取值为0.5。

本文针对小波基的正交性、紧支性、对称性、平滑性、消失矩阵阶数五方面特性对小波基进行选取。常用的小波有Haar小波、Biorthogonal小波、Daubechies小波、Symlet小波等。Haar小波是具有对称性的紧支正交实数小波，计算量很小，但是光滑性太差，在重构时会产生“锯齿”现象。Biorthogonal小波是具有对称性的紧支正交小波，但该小波系中各小波不具有正交性，只具有双正交性，因此计算的简单性和计算时间会受到影响。Daubechies小波是一类紧支正交小波，但该类小波对称性很差，导致信号在分解与重构时相位失真严重。Symlet小波是近似对称的一类紧支正交小波函数，在上述对称性不足之处进行了改进，使该小波系在处理信号时很大程度的避免不必要的失真。通过对小波系特性的分析，采用不同小波系的小波基对house图像进行实验，以原始图像和重构图像的信噪比作为评价标准，实验结果如表1所示。

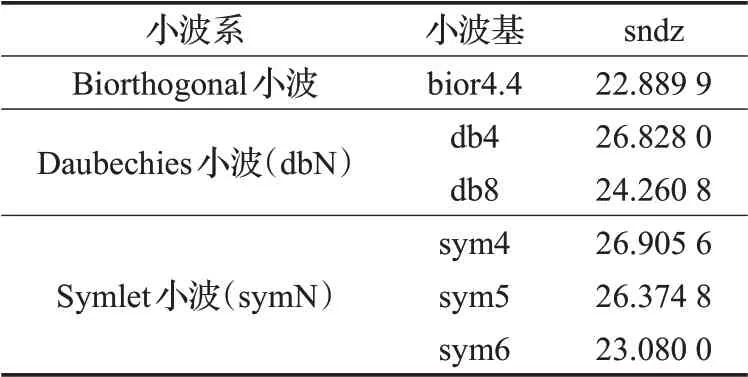
表1 采用不同小波基对house图像处理结果

观察表1可知，信噪比数值随着N（小波函数消失矩阶数）的增大而减小，图像在分解重构时失真严重。通过实验验证和综合分析上述小波系的不足及Symlet小波系针对对称性的改进，可知Symlet小波系的综合性较好，故本文采用sym4小波基进行分解重构。

3.1 验证去噪算法有效性

为了验证去噪算法的有效性，分别对含少量噪声的house（大小为768×512），room（大小为512×512）图像进行实验。同时为了保证实验结果的准确性，对小波分解后低频系数统一采用本文基于改进双边滤波的Retinex算法，在高频系数处分别采用软阈值函数、硬阈值函数、文献[14]函数及本文算法，重构后均采用分段性线性变换方法增强图像对比度。实验结果如图4、图5所示。为了更直观突出去噪对比效果，采用峰值信噪比（Peak Signal to Noise Ratio，PSNR）对去噪后图像进行数据对比。对比结果如表2，表3所示。PSNR值越大表示图像去噪效果越好。峰值信噪比公式定义如下：

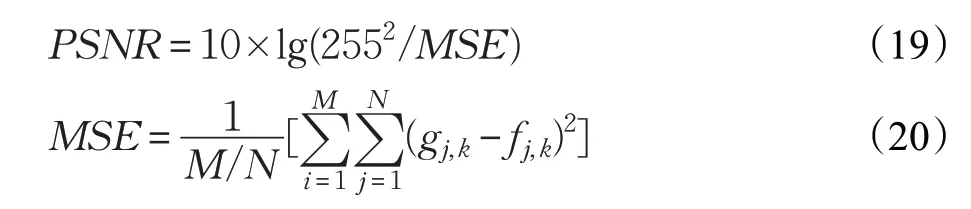
其中，M×N为图像大小，gj,k为去噪前图像，fj,k为去噪后图像，MSE为图像均方差。

表2 不同去噪算法对house图像去噪数据对比

表3 不同去噪算法对room图像去噪数据对比

由表2、表3数据可知，本文改进阈值函数去噪方法的PSNR值相对软阈值法、硬阈值法及文献[14]阈值法较高，具有较好的去噪效果，同时通过主观视觉观察可看出本文去噪方法在消除震荡现象的同时更好地保留图像细节信息。

图4 不同去噪算法对house图像处理结果

图5 不同去噪算法对room图像处理结果

图6 不同算法对boat图像增强结果

图7 不同算法对dog图像增强结果

3.2 验证增强算法有效性

为了验证增强算法的有效性，分别对含少量噪声的boat图像（大小为252×213）、dog图像（大小为252×213）进行实验。实验结果图像如图6、图7所示。

从主观视觉观察对比图6、图7可知，单尺度Retinex算法对含噪图像处理后易产生光晕现象和泛灰现象，如图7（b）自行车轮子上方边缘处产生光晕现象，图6（b）中图像整体泛灰，远处岸边与湖水对比度不明显，图7（b）中车圈与动物身体及地面对比度低。基于双边滤波的Retinex算法，加入了亮度差尺度参数，有效避免了光晕现象。但上述两种算法对含噪图像增强的同时，放大了图像的噪声，如图6（b）、图6（c）中水面与远处房子处，图7（b）、图7（c）中自行车轮子下方暗区域，均有明显的噪声放大现象。文献[5]算法在避免了光晕现象的同时更好地保留了图像的细节信息，但通过观察图6（d）、图7（d）可知，依然存在轻微泛灰现象。对比本文算法，对含噪图像增强之后，在避免了光晕现象的同时改善了泛灰现象，增强了图像的对比度，并且有效去除了图像噪声。

从客观数据分析角度，本文采用均值、方差、信息熵[17-18]作为图像质量评价标准。均值评价图像的整体亮度，图像整体亮度越高，均值越大。方差评价图像对比度，图像对比度越高，方差越大。信息熵用于评价图像的信息含量，图像信息含量越丰富，图像的信息熵越大。均值、方差、信息熵评价公式分别如下。

其中，M,N为图像大小，f(i,j)为图像像素值，pi为图像中灰度级为i的点出现的概率。

不同算法对boat图像、dog图像的增强结果在均值、方差、信息熵的数据对比如表4、表5所示。

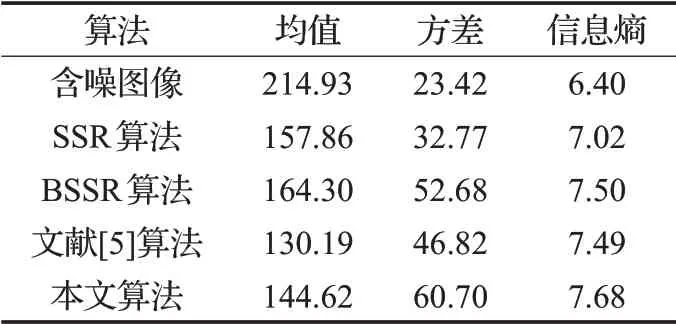
表4 不同算法对boat图像增强数据对比

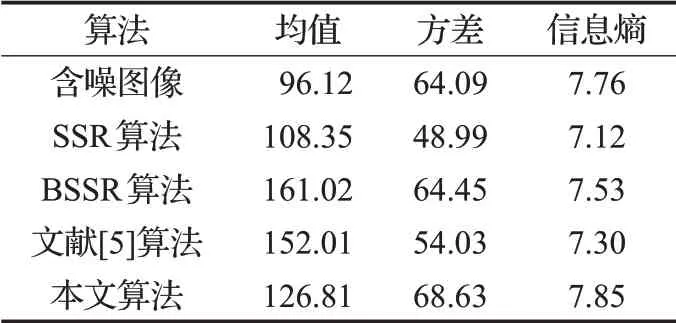
表5 不同算法对dog图像增强数据对比

由表4、表5可知，均值方面，表4中由于boat图像泛白，亮度较高，均值较大。为避免图像较亮区域产生过增强现象，本文算法对暗区域像素值进行少量压缩，亮区域像素值保持不变，所以本文算法均值较其他三种算法相对较低。方差方面，本文算法方差均高于其他三种算法，由于单尺度Retinex算法与文献[5]算法存在泛灰现象，方差相对较低，基于双边滤波的Retinex算法与原图像对比度相近，本文算法改善了泛灰现象，比较其他三种算法方差均有大幅度提升。信息熵方面，本文算法的信息熵值均高于其他三种算法，在增强后图像保有较高信息量。考量均值、方差、信息熵等评价因素综合分析可知，本文算法具有较好增强效果。

3.3 算法复杂度分析

在算法复杂度分析方面，单尺度Retinex算法和基于双边滤波Retinex算法中运算频率最高处均为光照图像估计部分，因此上述两种算法具有相同的算法复杂度，且估计光照图像部分决定着算法的运算效率。单尺度Retinex算法中采用高斯核函数进行光照图像估计，由于只考虑了像素点空间距离的度量，运算效率较高。基于双边滤波的Retinex算法中采用双边滤波代替高斯核函数进行光照图像估计，在考虑了像素点空间距离的度量的同时考虑了像素点间像素值的差异，运算效率相对较低。本文算法在低频系数处采用改进双边滤波代替高斯核函数进行光照图像估计，在空间上忽略了邻域内距离中心像素点较远点的处理，提升了一定的运算效率，同时在高频系数处采用改进阈值函数对图像进行去噪处理，有效去除了图像噪声，因此算法总体运算效率有所降低。单尺度Retinex算法、基于双边滤波Retinex算法及本文算法的运算复杂度如下。

（1）单尺度Retinex算法

时间复杂度：T(n)=O(n4+5n2)=O(n4)

空间复杂度：S(n)=O(1)

（2）基于双边滤波Retinex算法

时间复杂度：T(n)=O(n4+5n2)=O(n4)

空间复杂度：S(n)=O(1)

（3）本文算法

时间复杂度：T(n)=O(2n4+n2+1)=O(n4)

空间复杂度：S(n)=O(1)

为了更直观地观察各算法的运算效率，比较各算法的实时性，对单尺度Retinex算法、基于双边滤波的Retinex算法及本文算法处理单幅图像的耗时情况进行了测试，实验数据如表6所示。观察表6可知本文算法运算效率较低于上述两种传统算法。

表6 不同算法对dog图像、boat图像耗时对比

4 结束语

本文结合图像增强、去噪和小波变换的角度，提出了基于改进双边滤波的Retinex算法和改进阈值函数算法。采用改进双边滤波Retinex算法对小波分解后的低频图像进行光照图像估计，并得到反射图像，采用改进阈值函数得到小波分解后新的高频系数，去除图像噪声。运用分段性线性变化方法增强重构后图像的对比度。实验结果表明，在图像去噪方面，本文算法的改进阈值函数比软阈值函数、硬阈值函数及文献[14]函数具有更好的去噪效果，在图像增强方面，本文算法与单尺度Retinex算法、基于双边滤波Retinex算法和文献[5]算法相比，在消除了光晕现象和泛灰现象的同时具有较好的去噪效果，避免了噪声放大的问题。本文算法具有普适性，但未对特定领域图像进行有针对性实验，未有效满足固定领域需求，今后工作考虑将图像增强应用到某一特定领域，如医学图像处理、遥感图像、机器识别等做有针对性的图像处理。