模糊熵和深度学习在精神分裂症中的应用研究

田 程，胡 廷，曹 锐，相 洁

太原理工大学 信息与计算机学院，太原030024

1 引言

精神分裂症是一种病因未明的重性精神疾病，主要包括阳性症状，如妄想、幻觉；以及阴性症状，如认知障碍、思维紊乱等[1]，给社会和家庭带来严重的负担。科学研究表明：如果在患病早期能够准确诊断，有效治疗之后，大多数患者的病情可以得到控制，甚至康复。所以近年来该疾病受到社会和家庭越来越多的重视。

脑电图（EEG）是一种非侵入式和非放射性的工具，可长期测量大脑功能，因此广泛应用于临床疾病诊断。脑电反映大脑的活动状态，多用于辅助诊断大脑疾病，包括癫痫、阿尔兹海默症、精神分裂症等。同时，大脑是一个混沌系统，脑电信号具有非线性的复杂度特征，所以脑电信号的复杂性估计已经被广泛应用于疾病研究中。之前的研究采用Lyapunov指数（L1），香浓熵（ShEn），近似熵（ApEn）和Lempel-Ziv复杂度（LZC）等非线性指标发现精神分裂症患者与健康被试之间存在显著的复杂性差异[2]。在复杂性分析方法中，基于熵的算法是用于评估EEG规律性或可预测性的有效且稳健的评估器。2007年，Chen等人[3]改进了样本熵算法，引入模糊集后定义了一种新的测量时间序列复杂度的方法——模糊熵（FuzzyEn）。研究结果表明：脑电信号中的熵值测量可能更适合捕获人脑中不可察觉的变化。

最近，深度神经网络在图像、视频、语音和文本在内广泛的识别任务中取得了巨大的成就[4-5]。而卷积神经网络作为一种成熟的网络结构，近年来广泛应用于语音和图像识别领域。基于局部感受野和权值共享等优点，使得网络结构的复杂性大大降低，并且在脑电信号的检测中也得到了深入的研究应用[6-7]。

本文采用基于模糊熵和卷积神经网络的精神分裂症脑电信号分析方法，首先使用模糊熵对δ（0～3 Hz）、θ（4～7 Hz）和α（8～13 Hz）三种频段的脑电信号进行特征提取，统计检验后，选择存在显著性差异的电极作为卷积神经网络的输入，并优化网络的结构和参数，进一步从脑电数据中学习到更多的特征以提高分类精度。总体而言，所提出的方法旨在以熵和卷积神经网络为基础来揭示健康被试和患者EEG信号复杂性的差异，为精神分裂症的临床诊断提供科学有效的思路和途径。

2 材料与方法

2.1 研究对象

本实验所用的数据为来自北京回龙观医院的61名精神分裂症患者和与之年龄相匹配的55名健康被试，两组被试在年龄与性别以及受教育程度上均没有统计学差异。所有患者均符合美国精神障碍诊断统计手册第4版（DSM-IV）中关于精神分裂症的诊断标准[8]，并且取得患者和家属的同意。电极帽安放完毕后，被试静坐于隔音实验室中，头部和身体各部位保持静止，并尽量避免眼球运动。被试信息如表1所示。

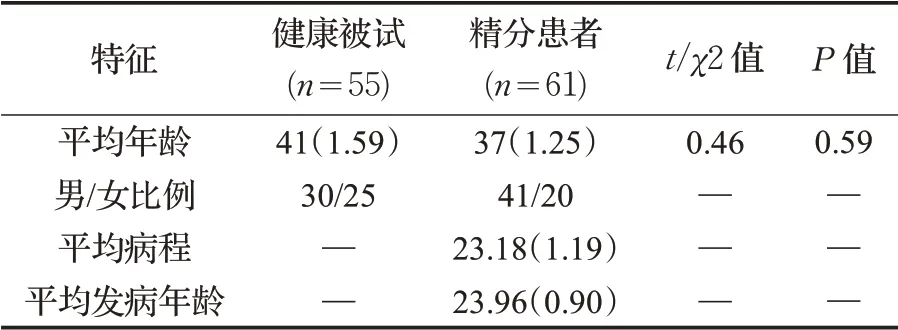
表1 被试信息表

2.2 数据记录

本研究按照国际心理生理学会提出的脑电信号记录原则与标准要求进行，实验室内隔音、安静。使用BrainProducts公司的脑电记录与分析系统，根据国际10/20系统记录64导EEG信号。电极的安放位置如图1所示。信号的采样频率为500 Hz，在安静闭眼状态下采集受试者的EEG信号。

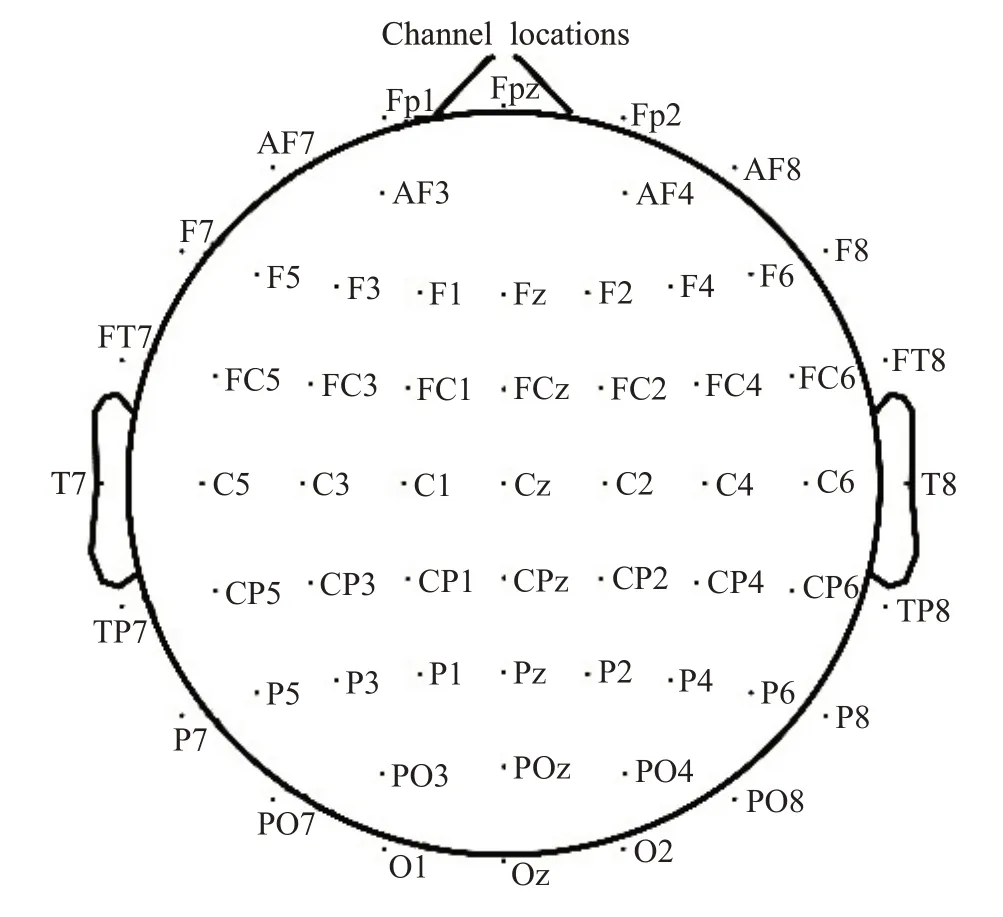
图1 国际10-20系统的电极位置

2.3 信号预处理

数据预处理通过Brain Vision Analyzer软件执行，首先对记录的原始EEG信号进行电极重参考，在事件相关电位（ERP）研究中不同的参考电极会产生不同的影响，因此选择常用于ERP数据预处理的所有电极的平均值作为参考；其次采用大小为0.5～50 Hz的滤波器对脑电信号进行滤波；眼电（EOG）对EEG信号影响很大，因此需要对由眼球运动或眨眼造成的肌肉影响进行矫正，从EEG信号中减去受EOG影响的部分。首先寻找EOG的最大绝对值，将最大值的百分比（10%）定义为EOG伪迹，其次将超过EOG伪迹的电位识别为EOG脉冲，取平均后得到平均伪迹，并计算与其他电极之间的EEG传递系数，最后根据系数对造成影响的波段进行校正；之后使用独立成分分析（ICA）方法进行伪迹去除，EEG信号包含由分离矩阵W混合而成的不同源信号，这些源信号包括自身活动、噪声等众多干扰源。首先为了简化算法，将EEG信号进行去均值操作，其次通过重复的迭代计算寻找适当的分离矩阵wi，使得函数N(si)获取极大值，便可得到一个独立分量si，分离过程中，不断调整分离矩阵，直到相邻两次的wi无变化或者变化较小时，结束对该独立分量的提取。重复上述分离过程，从EEG信号中减去每一个提取的独立分量，最终将所有独立分量分离出去；并将每个被试的时域数据截取60个长度为1.4 s的时间片段；最后将数据以.eeg的形式导出。整个实验流程图如图2所示。

2.4 模糊熵

在样本熵和近似熵算法中，由二值函数确定向量之间的相似性：

图2 实验流程图

给定一个输入样本，当符合一定条件时，根据二值函数将被判断属于其中一类，反之属于另一类。通常情况下，对于给定的一个样本，是很难判断其属于哪一类的，便引入了模糊集。模糊熵使用模糊隶属函数来测量向量之间的相似度，而不是基于样本熵算法的二值函数[3]。该函数为指数函数，由于指数函数是连续函数，保证函数值不会像二值函数一样产生突变，计算结果是平滑且连续的；并且与其他熵相比，模糊熵对相空间维数m和相似容限r等参数具有较低的敏感度，所测值的鲁棒性更高。该算法描述如下：

根据序列顺序对u()i进行相空间重构，得到一组m维(m≤N-2)矢量，如下：

模糊隶属函数如下：

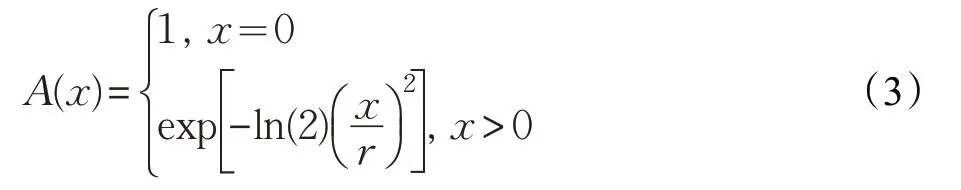
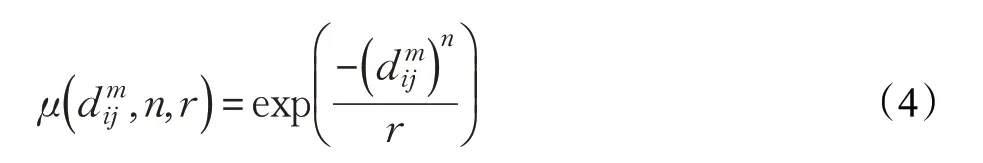
n和r分别表示指数函数的梯度和宽度。定义函数φ(n,r)：

并以相同的方式重复上述步骤，可以根据序列的顺序重建一组(m+1)维向量，将其定义为最后，序列长度为N的时间序列的模糊熵可表示如下：

通常情况下，过大的相似性容限会导致时间序列中有用信息的丢失，过低的相似性容限又会增加噪声的敏感度。在本研究中，通过进行参数调优，设置m=2，r=0.25×SD，其中SD为时间序列的标准偏差。

2.5 模糊熵特征提取

将预处理后的脑电数据分为δ（0～3 Hz）、θ（4～7 Hz）和α（8～13 Hz）三个频段；将三个频段的时间片段按照时间窗大小为400 ms，步长（窗移）为50%，截取6小段。选取400 ms是由于模糊熵适合于短数据集的处理，时间序列不适合选取太长，当使用300 ms、400 ms、500 ms的时间窗分别进行特征提取时，发现不同的长度对实验是有影响的，在400 ms下健康被试和精神分裂症患者的复杂度差异最大，所以最终选取400 ms作为时间窗大小。并尝试了五种不同的步长，分别是重复30%、40%、50%、60%、70%，结果显示，步长对实验结果的影响比较小，总体来说在50%步长下的结果是略好于其他情况的，所以选择了50%的步长；之后分别用模糊熵对每段400 ms的数据进行复杂度特征提取，分别计算出健康被试和精神分裂症患者在三种频段下连续的六个时间窗的熵值。用双样本T检验进行统计分析，从所有电极中选择出差异性最显著的32个电极(p＜0.05)。考虑到电极位置的空间分布特征，位于同一脑区的电极共同反映同一脑部活动，所以将位于同一脑区的电极相邻放置，进行排序；将每个电极三个频段的熵值按照时间窗的前后顺序进行排序，这样每个样本可以表示为32×18的矩阵。每个样本对应一个标签，患病为1，不患病为0。将其作为卷积神经网络的输入。如图3所示为卷积神经网络的输入数据影像图。

3 CNN算法及网络结构

卷积神经网络是一种用于生成特征层次结构的神经网络，有两大显著特点：稀疏连接和权值共享[9]。稀疏连接用于提取图像中不同区域的特征；权值共享则极大减少了网络中训练参数的个数和训练时间，简化网络结构。卷积神经网络的结构如图4所示。

3.1 卷积层

图3 输入数据影像图

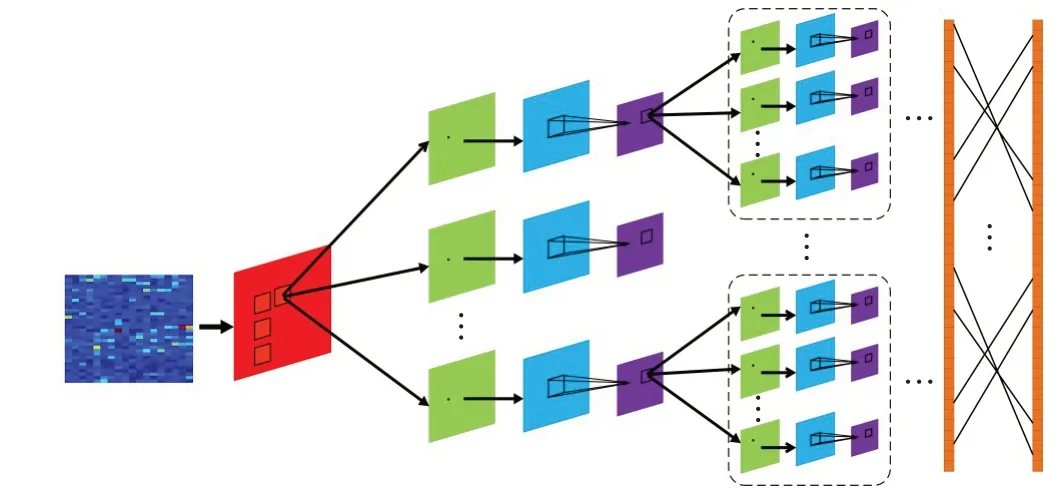
图4 卷积神经网络的结构

卷积层是网络结构的第一层，也是核心层。使用卷积核进行扫描，将输入神经元与网络权重相连，得到特定权值向量的特征图。卷积操作可以极大地减少网络参数，从而降低运算量。利用激活函数进行特征映射。激活函数加入了非线性因素来最大可能地保留数据的特征，本文中使用更优的Relu函数作为激活函数，研究表明Relu函数使得运算速度和运算效果得到明显提升。Relu函数表达式如下：

3.2 池化层

池化层的作用是将卷积运算得到的某一位置的输出由邻近值来取代，从而减少运算量。池化层中每个特征映射的平面上的神经元具有相等的权重，所以池化运算与卷积运算是类似的，通过激活函数得到采样层的输出。目前常见的池化方法包括最大池化（max pooling）和平均池化（mean pooling）。本实验中由于特征之间的差异比较大，所以采用了最大池化方法。

3.3 全连接层

全连接层的作用是整合卷积池化操作后得到的特征向量，也就是将输入的二维特征向量转化成一维向量。归一化处理后，输出到下一层作为分类器的输入。本实验将全连接层设置为两层，用于提升网络的学习效率，每层神经元数量设置为256个。

3.4 Softmax分类器

Softmax分类器是一种有监督的多分类器，是对逻辑回归模型的改进，得到的结果是一个概率值，即若存在样本数据x，通过Softmax便可计算其属于某一类的概率p，最终得到归一化的分类概率值。

3.5 卷积神经网络的学习过程

卷积神经网络的学习过程是一个不断优化网络中众多参数的过程，包括前向传播与后向传播。前向传播过程中首先对训练数据进行批处理（Batch_size），通过卷积层、池化层以及激活函数的前向传播后，得到输入信号的实际输出，此时完成了卷积神经网络的第一阶段的学习；在前向学习过程中，卷积核与偏置的值均为初始化值，所以实际输出结果与真实结果之间存在一定的误差，为了降低误差，需要计算平均误差代价函数来不断地更新权重与偏置，该过程为卷积神经网络第二阶段的学习。最终得到最优的网络学习模型。

本研究基于Theano框架评估了不同深度VGG风格的卷积神经网络配置。如图5所示，表中卷积层参数表示为Conv＜接收域大小＞＜内核数＞，A模型只涉及到两个叠加在一起的卷积层（Conv3-32）；B模型在A模型基础上添加了两个卷积层（Conv3-64）；C模型在B模型的基础上，再添加一个卷积层（Conv3-128）；模型D和模型C的不同之处在于第一个池化层前提供了四层卷积。最后在所有模型中添加两层含有256个节点的完全连接层，并使用Softmax函数作为分类器。

图5 不同CNN模型的配置信息

为了防止神经网络在学习过程中出现过拟合，本研究将Dropout技术引入到全连接层中。该技术可提高参数的泛化能力，从而防止训练参数对训练数据集的重度依赖[10]。经过参数调优，将学习率设置为0.01，Dropout的值设置为0.5，卷积核的大小为3×3，设置的迭代次数为20次。本实验采用了k-折交叉验证，k选取为10。训练集和验证集比例为9∶1。训练集用于训练拟合模型；验证集用于选择训练中得到的分类效果最优模型的参数，并进行参数调整；另外使用未参加过训练和验证过程的测试集来评价通过训练集和验证集得到的最优模型的性能与分类能力。最后将交叉验证的分类结果进行平均。

4 结果与分析

4.1 熵值特征

如图6所示为第一个时间窗（400 ms）的三种频段中模糊熵特征的脑地形图，从图中可以看到，在三个频段下，精神分裂症患者的熵值普遍高于健康被试。并且全脑的差异性很大。模糊熵是一种测量脑电信号中出现新模式概率的非线性方法，生成新模式的概率与脑电信号的复杂度呈正相关。相比于健康被试，精神分裂症患者由于自身大脑中的神经元处于兴奋和活跃状态，神经元做无序运动，所以患者大脑中产生新模式的概率较大，脑电信号的复杂性更高。统计检验的结果表明，两组之间在很多脑区中存在显著差异(t＜-15.159,p＜0.05)。而模糊熵具有更好的鲁棒性以及连续性，因此认为模糊熵作为输入特征进行分类能有效地区分健康被试和精神分裂症患者。

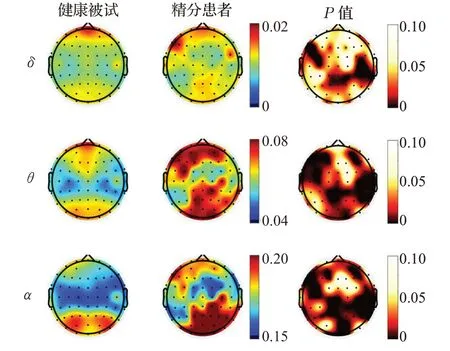
图6 模糊熵脑地形图

4.2 常规分类结果

本实验中首先使用了三种该领域常用的机器学习分类算法，包括支持向量机（SVM）、朴素贝叶斯（NB）以及随机森林（RF）。并且对分类器中的参数进行调优。SVM分类器的参数比较多，其中最重要的是惩罚参数c和核函数参数g两个参数。首先使用RBF核函数，研究表明该核函数相对稳定，其次对于一组取定的c和g，利用十折交叉验证的方法，选取准确率最高的那组c和g作为最佳参数，SVM分类器的参数为：c=1.0，g=0.125；NB分类器中主要选择参数估计方法，有极大似然估计和贝叶斯估计。由于极大似然估计可能导致估计出的概率为0，会影响后验概率的结果，所以NB分类器使用贝叶斯估计；RF分类器中有三个比较重要的参数，分别是最大特征数max_features、子树数量n_estimators和最小样本叶min_sample_leaf，使用交叉验证的方法得到不同参数组合下的分类准确率，并选择准确率最高的参数组合作为最佳参数，RF的参数为max_features=auto、n_estimators=60、min_sample_leaf=30。三种分类器的分类结果如表2所示。从表2中可以看到，三种分类器中分类效果最好的是SVM分类器，准确率达到了91.3%，而另外两种分类器的分类准确率分别为89.7%和87.6%。但是这三种分类器无法获取输入数据更深层次的隐含信息，分类准确率无法达到理想的效果。

表2 传统分类器的分类结果比较

4.3 深度学习分类结果

通过多次实验选择了四种不同深度的卷积神经网络框架。遵循VGG风格体系结构[11]，在每一层中选择合适的过滤器的数量，并且用较小接受域进行卷积操作。这四种模型的最终分类结果如表3所示，从表3中可以看到，不同深度的卷积神经网络的分类结果之间存在一定的差异。首先C＜2，2，1＞模型的分类准确率最高，并且准确率远高于传统分类器，验证集的准确率为99.23%，测试集的准确率为99.16%；D＜4，2，1＞与B＜2，2，0＞模型的准确率都低于上述模型；而A＜2，0，0＞模型的分类准确率最低，验证集准确率只有89.09%。4种模型的准确率箱图如图7所示，从图7中可以观察到不管是验证集还是测试集，C＜2，2，1＞模型的准确率分布情况均优于其他三种模型。以上结果表明神经网络的深度太深或者太浅都不能使分类效果达到最优状态，需要不断调试。

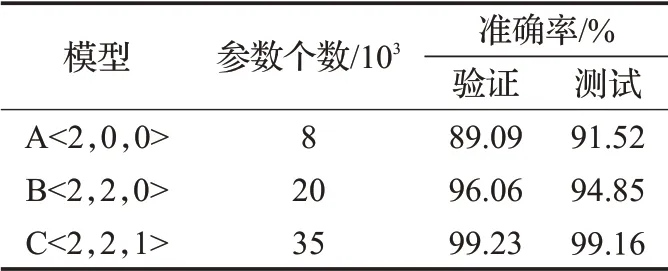
表3 不同深度CNN的分类结果比较

如图8所示为网络结构为C＜2，2，1＞模型的准确率曲线图和损失曲线图。从图中的分类准确率曲线可以看到，迭代次数不断增加，验证和测试准确率均呈现上升趋势，并且当迭代次数达到15次时，准确率趋于稳定，达到了99%以上；与准确率曲线相反，训练损失、验证损失以及测试损失在逐步减小，并且当迭代次数达到15次的时候，损失都达到平稳状态。训练得到的模型性能在验证集和测试集上效果都显著是实现良好拟合的基础，可以通过训练损失和验证损失同时下降并最终达到稳定状态进行判断，所以本实验训练得到的模型实现了良好拟合。

图7 验证集和测试集的箱图

图8 准确率和迭代损失曲线图

本实验中，卷积神经网络融合了脑电信号的非线性特征、时域、空域以及频域信息，经过模型优化，实验结果证明了本文模型在训练学习过程中的有效性。虽然该方法不是直接对原始EEG时间序列进行操作，但是通过从EEG中提取模糊熵作为非线性特征，能够发现EEG中更加隐含的信息。

4.4 同类研究比较

将本文的方法与其他关于精神分裂症的分类研究进行比较。比较结果如表4所示。文献[12]中通过记录多通道脑磁图（MEG）信号，并提取了最具识别性的δ、θ和α波段的功率谱值作为特征，使用SVM分类器进行分类，分类准确率为91.8%；文献[13]中采用互信息技术进行通道选择，该技术用于确定信息量更大的通道，从而获取更好的识别能力，自相关（AR）系数、频带功率以及分形维数作为信号的特征，最后使用Adaboost分类器进行分类，结果为91.94%；文献[14]中使用一种栈式自动编码器对患者和健康被试的功能性磁共振成像（fMRI）数据进行分类，分类准确率为92.00%；文献[15]中将离散小波变换（DWT）应用于EEG信号，提取的相对小波能量特征被传递到分类器用于分类，最后通过SVM、多层感知器以及K-最近邻分类器实现98%的分类准确率。但是本研究相较于以上研究，分类准确率得到了明显的提升。

表4 与其他分类结果的比较

5 结束语

模糊熵是一种基于复杂性的时间序列分析方法，模糊隶属函数使得测量的结果连续且平稳，能够使用较短的时间序列获得稳健的测量值，并且鲁棒性得到了很大提升。由于脑电信号的非线性特征，使用模糊熵可以提取出时间序列中更加隐含的信息。

本文提出了一种结合模糊熵和卷积神经网络的脑电信号分类方法，将脑电信号进行分频处理，之后将各个频段的每段时间序列分别用模糊熵提取信号的复杂度特性，选择存在显著差异的电极，并将熵值按照先后顺序排列构成影像图，作为神经网络的输入，可以学习到信号中更深层次的信息。最后使用Softmax分类器进行分类。实验结果表明，复杂度可以更好地提取健康被试和精神分裂症患者中脑电信号的非线性特征，并能够检测到两类被试间存在的显著差异，通过对卷积神经网络进行参数调优和性能优化，训练出更优的模型，最后分类结果显示，与传统的分类算法相比，该方法下分类准确率得到明显提升。该方法能够更好地辅助精神分裂症的临床诊断，并可以应用到其他疾病诊断中，为临床疾病诊断提供更加科学高效的措施。