半监督学习的运动想象脑电信号分类

谭学敏，郭 超

1.成都信息工程大学 控制工程学院，成都610225

2.国网成都供电公司，成都610041

1 引言

脑机接口（Brain Computer Interface，BCI）是一种能让大脑和计算机或其他通讯设备之间进行通讯的系统。1973年，Vidal[1]第一次提出了BCI这项技术，是为了帮助有着严重运动障碍的患者能够控制外部设备，实现与外部世界的交互。在BCI系统中获得未标记样本是比较容易的，但是收集标记样本却比较困难，因为标记样本是耗时且昂贵的[2-3]。因此，在BCI竞赛III中，其中一个任务就是需要减少训练进程。而且脑电信号的状态也会随着时间发生变化，使得分类难度进一步升高。在本文中，使用了半监督学习来解决运动想象脑电数据的分类问题。与监督学习相比，半监督学习只需要利用少量标记样本和大量未标记样本来训练分类器并提高分类器的性能，这样很大程度上减少了标记样本所需要的时间和费用。而且半监督学习本身是一个自适应的过程，有助于促进BCI自适应性的增强。近些年，半监督学习逐渐成为了机器学习和模式识别领域重要的研究方向，并吸引着越来越多的学者研究和分析。目前主要的半监督方法包括自训练算法[4]、协同训练算法[5]、生成式模型算法[6]和直推式支持向量机[7]等。

Deng等[8]提出半监督学习的其中一个必要条件是从训练数据中提取出的特征需要有足够的鲁棒性。当前，共空间模式（Common Spatial Pattern，CSP）和滤波带宽共空间模式（Filter Bank Common Spatial Pattern，FBCSP）这两种算法被广泛应用在BCI的特征提取中，尤其是CSP算法应用最多。

Yuan等[9]证明了CSP特征具有足够的鲁棒性，是一种比较先进的特征提取算法。这一算法的成功主要归功于事件相关同步/事件相关去同步（ERD/ERS）的神经生理现象。虽然CSP和FBCSP算法在提取脑电信号方面已经获得很好的效果，但是只是经验性地选取有用的数据段，没有充分考虑脑电信号中所有有用的数据段。如果不适当地选择数据段，那么很有可能遗漏有用的信息或加入不适当的信息，导致分类性能的下降。因此，在本文中，提出了一种先进的特征提取方法——分段重叠共空间模式（Segmented Overlapping Common Spatial Pattern，SOCSP），能够获得比CSP和FBCSP鲁棒性更好的特征。

在半监督学习的迭代过程中，分类器性能提高的两个阻碍原因是：（1）标记样本过少导致训练不出可靠的初始模型；（2）误标记用来更新初始模型的未标记样本。因此，如何从未标记样本中找出置信度高的样本是个需要解决的问题。Cuan等[10]提出了一种基于图与瑞利系数最大化的半监督算法，但此算法初始模型的准确性不够，随着迭代的增加，初始模型不仅得不到优化，反而将预测错误向后传播。Li等[11]在P-300的脑机接口系统中使用了一种基于SVM的半监督算法，并且获得了比较满意的结果。此算法虽然保证了初始模型的准确性，却没有考虑每次迭代未标记样本的置信度问题，增加了误标记未标记样本的概率，可能导致分类器性能的下降。为了解决这个问题，提出一种新的置信度评估准则，从未标记样本中找到置信度高的样本，提高分类器性能。

众所周知，Fisher线性判别分析（Fisher Linear Discriminant Analysis，FLDA）和支持向量机（Support Vector Machine，SVM）是常见的分类器。在本文中，选择FLDA作为分类器，因为在相同情况下FLDA能够获得与SVM相差不多的分类率，而且不需要像SVM一样提前设定参数[12]。

因此，本文提出了一种基于SOCSP特征提取的自训练算法ST-SOCSP（Self-Training base Segmented Overlapping Common Spatial Pattern，ST-SOCSP），使用SOCSP作为特征提取方法，FLDA作为分类器，使用新的置信度准则从未标记的样本中选择信息量大的样本添加到标记样本中重新训练分类器，将ST-SOCSP应用到BCI竞赛的数据集Iva中验证算法的有效性，结果表明了提出的算法能有效提高运动想象脑电的分类率。本文创新之处在于提出了先进的SOCSP特征提取算法与半监督算法结合和新的置信度准则避免未标记样本的错分。

2 基于SOCSP特征提取的自训练算法（ST-SOCSP）

2.1 共空间模式（CSP）

为获取最佳投影方向，使得两类信号的区别最大，共空间模式（CSP）设计了最优的空间滤波器。原理介绍如下：

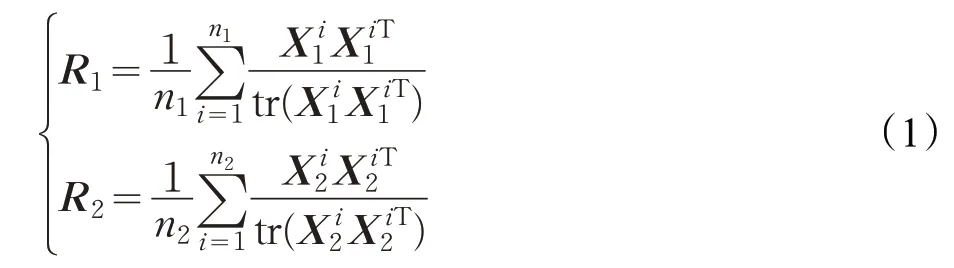
其中，tr(·)为矩阵对角元素之和，两类的平均协方差矩阵之和为：R=R1+R2，对R进行特征值分解：R=UλUT，其中U和λ分别代表特征向量矩阵和对角矩阵。利用U构造白化矩阵P后，R1和R2变换如下：

对S1和S2进行特征值分解，且S1和S2对应的特征值之和为1。

B表示S1和S2共有特征向量，而Λ1和Λ2分别代表S1和S2的特征值对应的对角矩阵。矩阵S1的特征值在最大方向上时，矩阵S2对应的特征值最小，反之亦然，这时两类信号的区别最大。投影矩阵W=BTP，通过投影，原始信号转换成新的信号Z=WX。

实际应用中，W的前m和后m行构成最佳滤波器矩阵。对产生新信号做对数规范化处理后，可以得到特征：

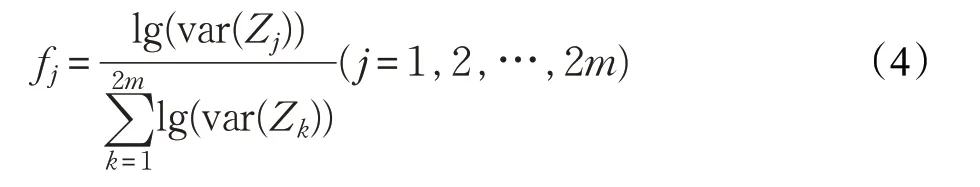
2.2 Fisher线性判别分析（FLDA）

实际应用中，线性判别式分析（Linear Discriminant Analysis，LDA）作为一种常用的模式识别方法，需要根据实际情况寻找判别准则函数，使得在这个函数投影下的样本在新空间中的类间离散度最大而类内离散度最小[13-14]。线性判别函数的一般表达式如下：

x表示某个样本特征向量，W为权向量，w0表示阈值权。根据函数y(x)的判别分数，两类问题的决策规则如下：

y(x)=0定义了超平面，也叫决策面，超平面把属于w1和w2的点分隔开，目的是为了找到最佳权向量W和阈值权w0。

Fisher准则的最终目标是将样本投影到一维空间后，使得类内离散度Sw减小，而类间离散度Sb增大，Fisher判别准则定义如下：

为了使分子最大化和分母最小化，需要求解向量W来使J(W)最大化。使用拉格朗日求解法求解上式，可得出：

根据投影方向向量W，将原空间向量投影到一维空间，w0一般利用先验知识求解，在这里w0=-WTm。

2.3 分段重叠共空间模式（SOCSP）

目前，有很多与BCI相关的文献均引入了CSP和FBCSP算法，尤其是CSP算法。虽然CSP和FBCSP算法在提取脑电信号方面已经获得很好的效果，但是它们都只是经验性地选取有用的数据段，没有充分考虑脑电信号中所有有用的数据段。如果不适当地选择数据段，那么很有可能遗漏有用的信息或加入不适当的信息，导致分类性能的下降。为解决这个问题，本文提出一种新的特征提取方法——分段重叠选择共空间模式（SOCSP）。在描述SOCSP算法之前，先介绍下Davis-Bouldin指标（Davis-Bouldin Index，DBI）的概念。

DBI[15]目标是从众多特征中挑选出相似度最小的特征。通过计算类内离散度(Wi和Wj)和类间离散度(Iij)，可以衡量两类信号的相似度。

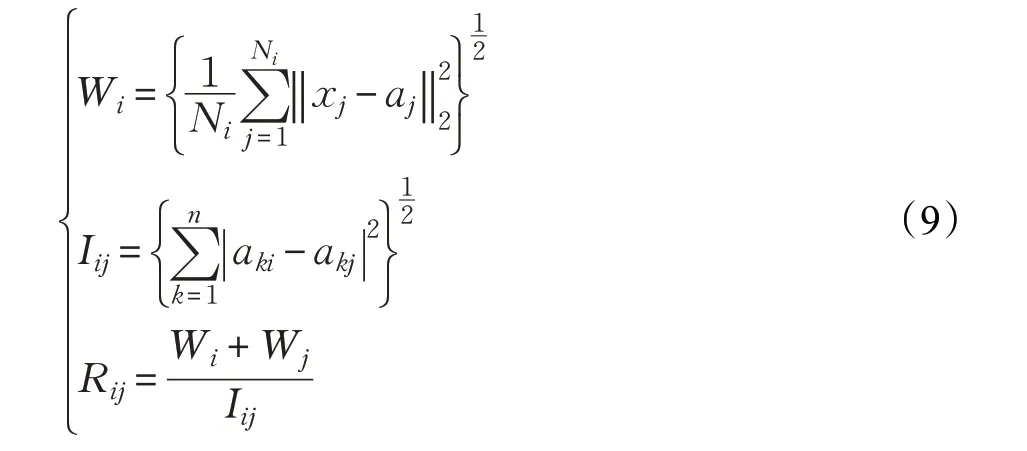
xj和Ni分别表示第j个样本的特征和聚类i包含的样本数。ai=[a1i,a2i,…,ani]是聚类i的中心，n为样本维度。各个特征对应DBI的值为：

C表示聚类的类别数，DBI值越小，聚类相似度越低，两类分类效果越好。将所有特征对应的DBI值按升序排列，最好的特征拥有最小的DBI值。

介绍完DBI概念后，提出了SOCSP算法，它能克服了CSP和FBCSP算法可能数据段选择不当导致分类率性能降低的缺点。SOCSP算法步骤描述如下：

（1）由于脑电信号的非平稳性，将脑电信号时间长度划分为n个有重叠窗口的时间段。

（2）原始脑电信号经过8～30 Hz的数字带通滤波。

（3）为减少伪迹和噪声，利用共同平均参考法（Common Average Reference，CAR）[16]对经过滤波的脑电信号进行预处理。

（4）使用CSP分别提取n个时间段脑电信号的特征。CSP转换之后，使用投影矩阵W（见公式（8））的前两行和后两行提取规范化的特征，这样各个时间段的脑电信号被提取了4个特征，那么n个时间段提取4n个特征。

风俗画作品不论是在中国还是西方，都在展现其审美价值的同时提供着超出审美意义本身的丰富的艺术价值。而对于中、西方风俗画作品来讲，在某种意义上，他们也都具有提供特定社会阶层生活细节的价值。

（5）计算4n个特征对应的DBI值，选择m个最小DBI值所对应的特征。

为了更清晰地了解SOCSP算法，流程图如图1。

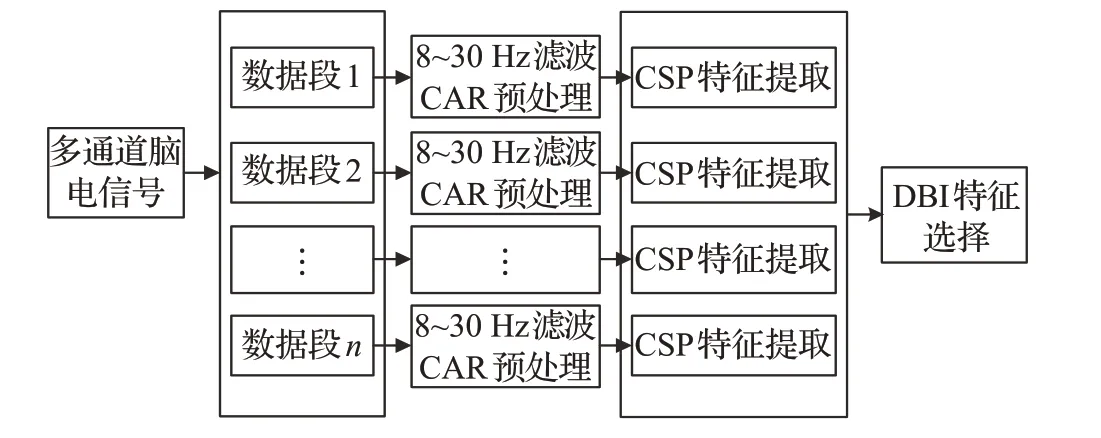
图1 SOCSP算法流程图

2.4 置信度评估准则

在半监督学习的迭代过程中，两个阻碍分类器性能提高的原因是：（1）标记样本过少导致训练不出可靠的初始模型；（2）误标记用来更新初始模型的未标记样本。因此，如何从未标记样本中找出置信度高的样本是个需要解决的问题。提出了置信度评估准则来找到这些样本。

从公式（5）中可以看出，经过FLDA分类器的训练，所有样本都预测得到相应的判别分数。在本文的半监督学习中，置信度高的未标记样本才能够用来扩展训练集。使用初始训练样本训练FLDA分类器，得到标记样本(DI)和未标记样本(DF)的判别分数。根据FLDA的原理，推断得出与某类中心(mean1或mean2)有最小距离的同类预测未标记样本有更高的置信度。在这里：

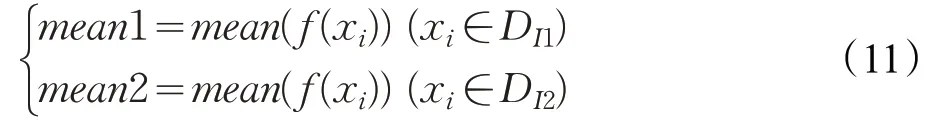
其中mean1和mean2分别被称为类中心1和类中心2，表示训练集DI中类别1和类别2的类中心。DI1和DI2分别表示训练集DI中属于类别1和类别2的训练集。明显地，DI=DI1⋃DI2。

通过分析DI和DF得到的FLDA判别分数，从DF中挑选置信度高的样本。置信度评估准则说明如下：

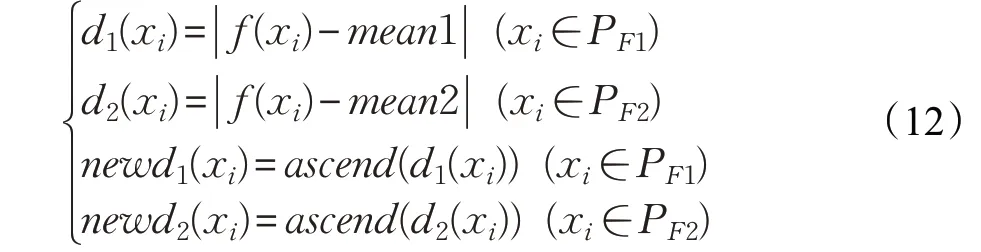
PF1和PF2分别表示预测结果属于类别1和类别2的未标记数量集，明显地，DF=PF1∪PF2，预测结果为类别1的未标记样本的判别分数f(xi)与训练样本中的类中心1的距离d1(xi)，表示预测为类别1的各个未标记样本的置信度，d2(xi)则表示预测为类别2的各个未标记样本的置信度。newd1(xi)和newd2(xi)分别表示d1(xi)和d2(xi)的升序结果，结果越小，置信度越高。

2.5 置信度评估准则基于分段重叠选择共空间模式的自训练算法

初始化：用SOCSP特征提取算法提取初始训练集DI和DF中所有样本的特征。使用DI中样本的特征和其对应的标签训练FLDA分类器，并预测DF中所有样本的判别分数，得出样本类别，标记为[yk(1),yk(2),…,yk(N2)]。k代表第k次迭代，这里k=1。

迭代步骤：步骤1到4描述了第k次迭代的过程(k=2,3,…,K0)。

步骤1（更新训练集）根据置信度评估准则，当第k-1次迭代时，从扩展训练集DF中挑选置信度高样本，记作Qk，并预测标签。因此，第k次迭代中，初始训练集DI（已标记）和Qk（预测标签）构成了新的训练集

步骤2（重新提取特征）利用SOCSP重新训练再重新提取初始训练集DI和DF中所有样本的特征。

步骤3（分类）根据新的训练集中提取出的所有样本的特征和其对应的标签，训练FLDA分类器，在DF上预测得出的判别分数记作fk(x)(x∈DF)，其对应的类别记作[yk(1),yk(2),…,yk(N2)]。

步骤4（停止条件）当k=K0时，算法在第K0次迭代后终止，其中K0是迭代的次数。[yk(1),yk(2),…,yk(N2)]是扩展训练DF最终预测类别。否则跳回步骤1执行第k+1次迭代。

本文中，从预测为正类的未标记样本和预测为负类的未标记样本中分别挑选80%置信度高的样本添加到标记样本中。

为了清晰地表示出提出的ST-SOCSP算法的过程，见流程图2。

3 实验数据描述与处理

本文使用2005 BCI竞赛的数据集Iva[17]，分析了想象右手运动和想象右脚运动两类过程中，5个受试者的脑电数据。这次竞赛提供了5个受试者想象右手和右脚运动的数据，总共包括280个样本。所有算法在配置为2.9 GHz 8 GB电脑的2016 MATLAB上执行。

在本文中，各个受试者前200个样本作为训练集T，剩余80个样本作为独立测试集TS。训练集T由已标记的初始训练集DI和未标记的扩展训练集DF组成，T=DI⋃DF。在训练集T上执行ST-SOCSP，其中随机选择20（40，60，100）个样本用作初始训练集DI，剩余180个（160，140，100）样本用作扩展训练集DF。然后将这200个训练样本随机排序，使ST-SOCSP总共进行30次训练，独立训练集TS用来测试分类器的性能。

图2 基于分段重叠选择共空间模式的自训练算法（ST-SOCSP）

对每个样本数据，根据国际10-20导联系统的电极分布，选择22通道（对应想象运动区域，见图3）的数据并分析每通道3.5 s运动想象数据，然后使用SOCSP算法提取样本特征。其中，将3.5 s运动想象数据划分1 s的时间窗口，0.5 s的窗口重叠，导致有6个时间窗口数据，24个CSP特征（每个时间窗口提取了4个CSP特征），然后使用DBI选择6个对应最小DBI值的特征。这里之所以选择6个特征，是因为之后会对CSP和SOCSP结合半监督进行比较，而对CSP算法来说，提取超过6个以上的特征不能够有意义地提高分类表现[18]，这样选择6个特征使得CSP与SOCSP结合半监督算法的对比更加公平。

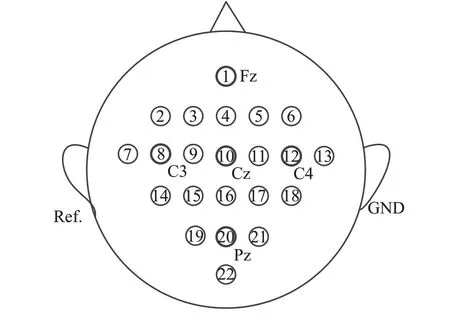
图3 国际10-20导联系统的电极分布

4 实验结果与分析

4.1 监督学习与半监督学习的比较

比较了静态分类（属于监督学习）（Static Classification，STC）和基于SOCSP的自训练算法（Self-Training based SOCSP，ST-SOCSP）在分类率上的表现。这两种算法均使用SOCSP提取特征，也均在独立测试集TS上测试各自的分类率。两种算法不同之处在于，对于STC，仅仅使用初始训练集DI训练FLDA分类器；对于ST-SOCSP，首先利用初始训练集DI训练FLDA分类器，然后挑选扩展训练集DF中80%预测置信度高的样本，并且迭代地添加这些样本到初始训练集中重新训练分类器。

BCI Iva数据集的STC和ST-SOCSP的仿真实验结果如表1所示。表1比较初始样本分别为20、40、60、100的时候，各个受试者在STC、ST-SOCSP结束后所获得的平均预测分类率。为了比较每个受试者获得分类率的显著性，表1中列出了具有统计学意义的p值（在表1中表现为p1）。当p值小于0.05时说明对比具有显著性意义。从表1中可以清楚地看到在初始样本分别为20、40、60、100的情况下，大多数受试者的ST-SOCSP的分类率比STC有很大的提升，这意味着半监督学习可以通过标记相同数量的样本达到比静态学习更好的分类率。从表1中，也观察到随着未标记样本的加入，其他受试者的ST-SOCSP分类率是高于STC的，但被试3的表现却不同，这可能是因为初始分类器的分类性能太差，导致不能在置信度评估准则的帮助下从扩展训练集中选择到置信度高的样本来提高自身的表现，反而给分类器的训练引入了噪声，随着迭代增加造成噪声的积累，使得被试3的ST-SOCSP分类率低于STC。除此以外，从表1中的p1值可以观察到，对大多数受试者来说，ST-SOCSP相比STC分类率是有显著性提高的。

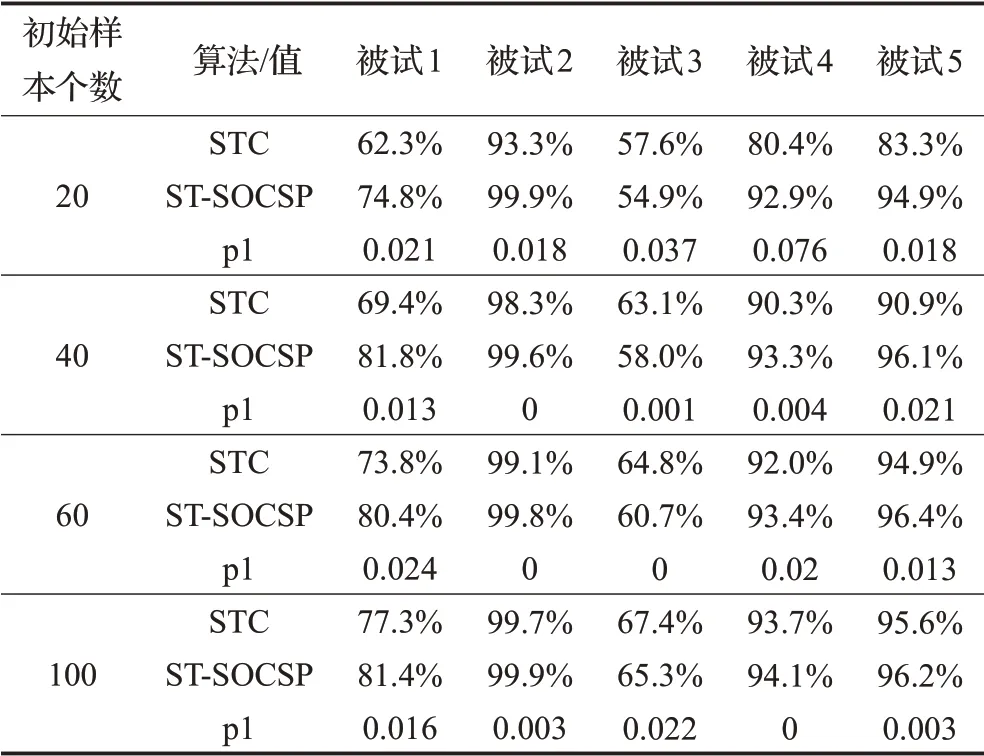
表1 不同初始样本下STC和ST-SOCSP平均分类率

4.2 三种半监督算法的比较

比较了三种特征提取方法结合半监督算法得出的分类率。这三种特征提取算法分别是CSP、FBCSP和提出的SOCSP算法。称这三种结合自训练的算法为ST-CSP、ST-FBCSP、ST-SOCSP，将这200个训练样本随机排序，这三种算法分别进行了30次训练，独立训练集TS用来测试分类器的性能。三种算法的训练过程同样也使用了置信度评估准则。

表2比较了在初始样本分别是20、40、60、100的情况下，30次训练后，各个受试者在ST-CSP、ST-FBCSP、ST-SOCSP这三种算法上的平均分类率。从表2中可以看出，无论初始样本是多少，对大多数受试者来说，ST-SOCSP比ST-FBCSP和ST-CSP能够获得更好的分类率，这充分证明了SOCSP特征提取算法的有效性。表2中也列出了具有统计学意义的p值、p2和p3分别表示ST-SOCSP和ST-CSP、ST-SOCSP和ST-FBCSP对比得出的p值，可以看出，对大多数受试者来说，ST-SOCSP相比ST-CSP和ST-FBCSP是有显著性提高的。

另外，对ST-FBCSP，初始样本为20和40的时候，除被试1（初始样本40）外，其他受试者在ST-FBCSP上获得的分类率比不上ST-CSP。但当初始样本达到60、100时，ST-FBCSP和ST-CSP分类率相差不大。在表3中报告了初始样本为200（训练样本只有200个，这种情况等同于监督算法）时，CSP、FBCSP、SOCSP作为特征提取方法，通过监督方法训练出FLDA分类器，在独立测试集上获得的平均分类率。可以发现，当训练集样本的个数达到200个时，FBCSP作为特征提取方法获得的分类率是高于CSP的，但依然赶不上SOCSP。这说明了FBCSP这种方法对初始分类器是比较敏感的。样本越多，训练出的初始分类器越好，FBCSP的表现越好。从表2中也能发现，对ST-SOCSP来说，随着初始训练样本的增加，每个受试者的分类率是在逐步增加的，对STCSP和ST-FBSOCSP也有相同的规律。这说明了初始样本的数量决定了初始分类器的好坏，初始分类器的表现决定了能否从未标记样本中选择置信度高的样本来进一步改善分类器的表现。

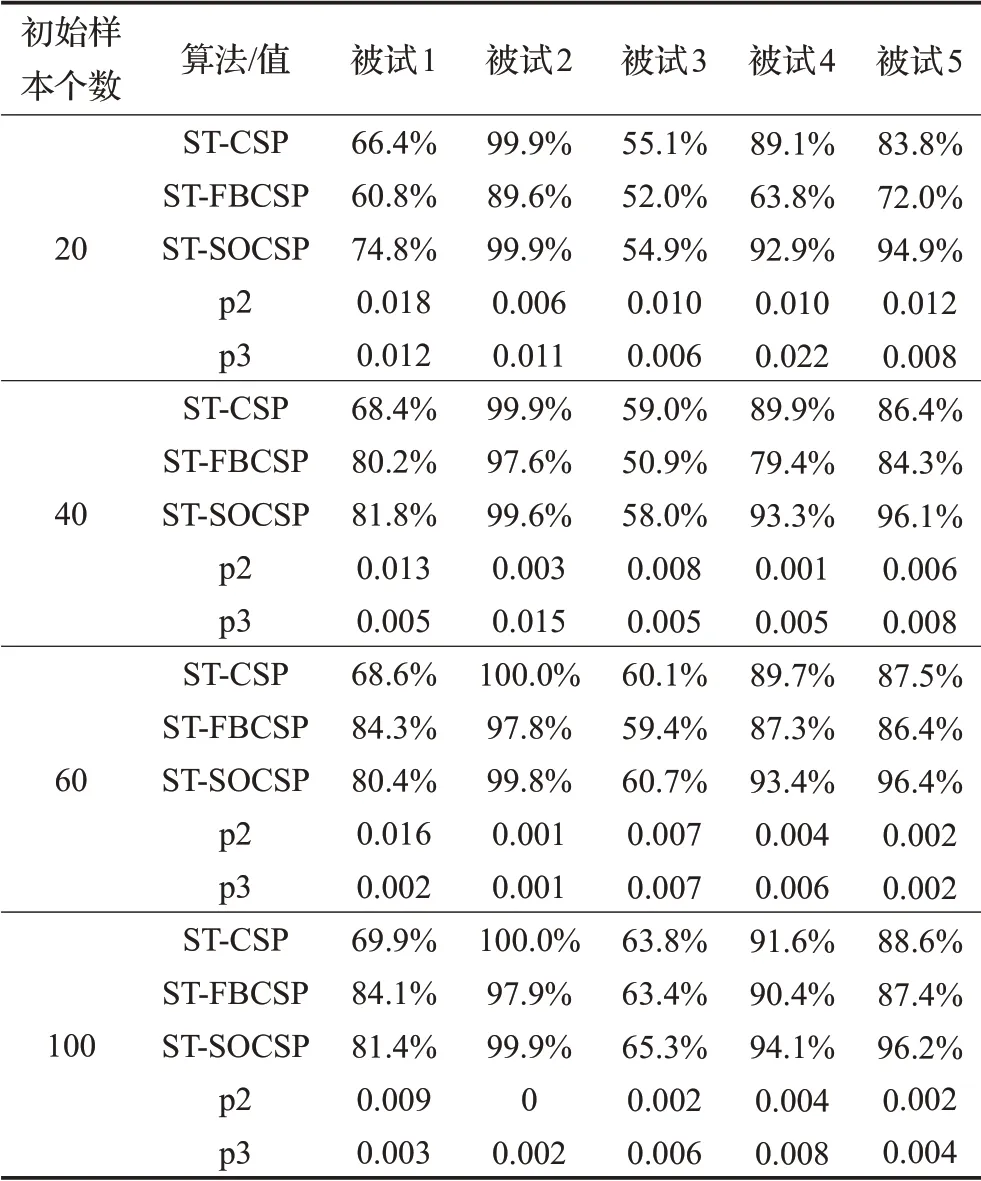
表2 不同初始样本下ST-CSP、ST-FBCSP、ST-SOCSP的平均分类率

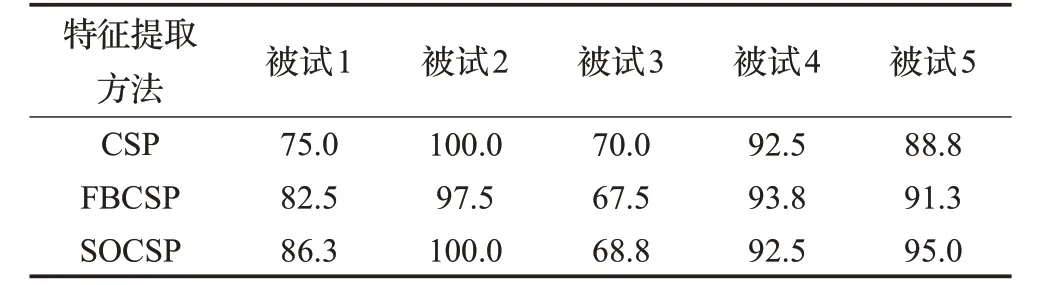
表3 初始样本为200时三种特征提取方法下的分类率%

4.3 三种半监督算法使用时间比较

众所周知，在运动想象BCI的实验中，收集运动想象EEG是一个枯噪和疲惫的过程，训练花费时间越少，越能减少令人感到枯噪和疲惫的训练时间。表4报告了在不同初始样本的情况下，执行ST-CSP、ST-FBCSP、ST-SOCSP所使用的平均时间。注意这里报告的时间是30次训练所使用的平均时间。可以发现，无论初始训练样本多还是少，对各个受试者来说，ST-CSP所花费的时间是最少的，其次是ST-SOCSP，花费时间最多的是ST-FBCSP。对ST-SOCSP来说，虽然花费的时间超过了ST-CSP，但从表1可以看出，ST-SOCSP获得的分类率是远远高于ST-CSP的。但对ST-FBCSP来说，虽然展示了初始样本达到60，100时，它的分类率勉强能够与STCSP持平，但是花费的时间却大大高于ST-CSP。

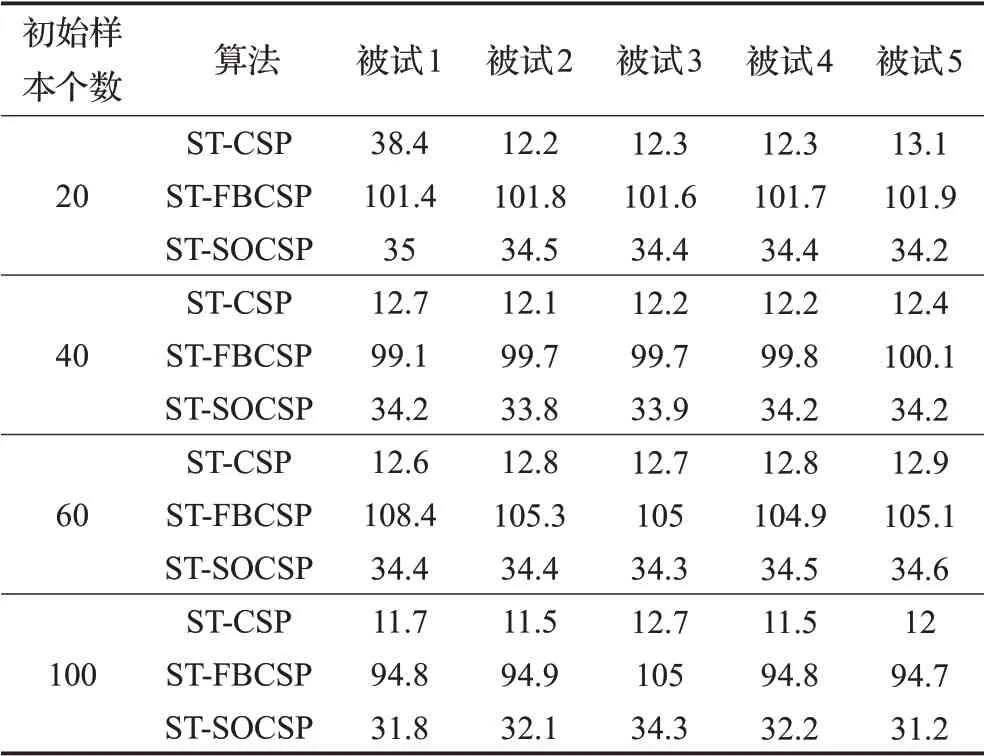
表4 不同初始样本下ST-CSP、ST-FBCSP、ST-SOCSP的平均花费时间 s

4.4 置信度评估准则的有效性

为了说明ST-SOCSP在置信度评估准则上的有效性，表5也比较了在不同初始样本情况下（20、40、60、100）使用置信度评估准则的ST-SOCSP与没有使用置信度评估准则的ST-SOCSP的表现。未使用置信度评估准则的ST-SOCSP算法每次迭代都是随机从未标记样本中选择80%的样本，而使用置信度评估准则STSOCSP算法每次迭代都是使用置信度评估准则从未标记样本中选择80%的样本。显而易见，不论初始样本的尺寸，对大多数受试者来说使用置信度评估准则的STSOCSP算法的表现是好于未使用置信度评估准则的ST-SOCSP算法。这是因为随机选择样本会导致选择未标记样本池中表现不好（置信度低）的样本，这些样本会破坏算法的性能。实验结果证明了提出的置信度评估准则在提高分类率上的有效性。从表5的p4值可以看出，对大多数受试者来说，使用置信度评估准则的STSOCSP算法相比未使用置信度评估准则的ST-SOCSP算法是有显著性提高的。

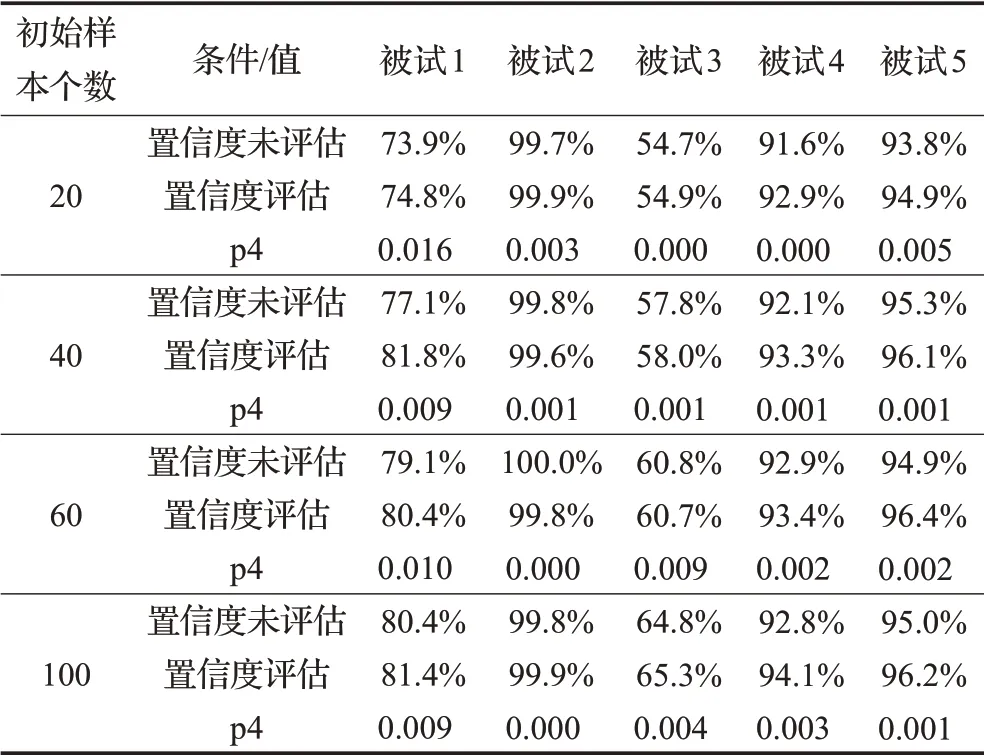
表5 置信度评估准则对ST-SOCSP平均分类率的影响

5 结论

本文提出了一种基于SOCSP的自训练算法（STSOCSP），创新点如下：提出了一种置信度评估准则，使用FLDA得出的判别分数来选择置信度高的样本，提出与某类中心（mean1或mean2）有最小距离的同类预测未标记样本有着更高的置信度。提出了一种先进的特征提取算法SOCSP，并将其结合到自训练中获得的更好的分类效果。将ST-SOCSP算法应用到2005 BCI竞赛的数据集Iva的五个受试者上，ST-SOCSP的表现是超过了ST-FBCSP和ST-CSP，而花费的时间只是略高于ST-CSP，但分类率远远高于ST-CSP。其次，使用置信度评估准则的ST-SOCSP也比未使用置信度评估准则的ST-SOCSP获得更高的分类率。这都充分证明了SOCSP特征提取算法和置信度评估准则的有效性，更是证明了提出的ST-SOCSP算法的有效性。