基于时间误差的循环神经网络参数压缩

王龙钢，刘世杰，冯珊珊，李宏伟

中国地质大学（武汉）数学与物理学院，武汉430074

1 引言

序列数据处理是机器学习中一个极具挑战性的问题，而循环神经网络（Recurrent Neural Networks，RNN）对序列数据的处理是强有力的，它广泛应用于机器翻译[1-2]、语音识别[3]、图像标注[4]等自然语言处理和计算机视觉领域。

基于循环神经网络的语言模型通常包含词嵌入层、循环网络层和全连接层等。这些网络层次通常包含大量的参数。例如，在机器翻译模型中，参数可能会有数百万乃至上千万个[1-2]。如此庞大的参数规模将消耗较多的存储资源。在这种情形下，将这种参数规模庞大的模型应用于移动电话或嵌入式设备是一个比较困难的任务[5-7]。

为了减小模型参数规模与内存成本之间的矛盾，模型的参数通常需要被有效的压缩。压缩深度神经网络参数需要在网络参数规模和网络性能之间的保持平衡，即在尽可能保持网络性能的基础上压缩参数规模。

深度神经网络参数的压缩目前已有多种思路。文献[8]用二进制数代替神经网络参数来减小参数规模。文献[9]通过训练软目标来代替硬目标，实现将较大的参数规模压缩成较小的参数规模。由于张量分解可以用较少的参数表示张量而只损失较少的信息，不少文献将张量分解用于压缩深度神经网络。文献[5，10]分别将张量列（Tensor Train，TT）分解用于循环神经网络和卷积神经网络（Convolutional Neural Networks，CNN）的压缩。文献[11]提出了神经网络压缩的新思路。它将卷积神经网络压缩分为3个过程，首先对网络进行裁剪，保留重要的连接，使权矩阵变得稀疏；然后对权矩阵进行聚类，属于同一类的共用一套权值；最后再用Huffman Coding进行压缩。该方法可以将网络压缩数倍且基本保持网络的性能。低秩方法也是网络参数压缩的方法之一。文献[6，12]采用低秩的权矩阵代替原始权矩阵，用较少的参数表示网络且不使网络性能下降明显。

与卷积神经网络相比，循环神经网络处理的数据通常含有时序特性。因此，压缩循环神经网络时考虑数据的时序特性，将有可能提高压缩效果。受文献[6-7]的启发，本文在低秩压缩方法的基础上，通过构建基于时间误差的重构函数来进行压缩。该误差重构函数在低秩误差重构的基础上，增加了时间误差重构项，并引入了长短时记忆（Long Short-Term Memory，LSTM）网络[13]中的门限激活机制。最小化该误差重构函数，可以提升模型压缩后的性能。该方法在多个数据集上取得了较好的实验结果。

2 低秩重构压缩

设W∈Rm×n，rank(W)=r，则存在一个分解使得：

其中U∈Rm×r、V∈Rn×r是正交矩阵，Σ=diag{σ1,σ2,…,σr}∈Rr×r是对角矩阵，且σ1,σ2,…,σr为矩阵W的奇异值，σ1≥σ2≥…≥σr≥0。

其中P=US∈Rm×r，Q=VS∈Rn×r。

式（2）中，P和Q一共有( )m+n r个参数，W有mn个参数。当r较小时，将有( )m+n r＜mn，式（2）说明可用较少参数的矩阵P和Q来表示一个参数较多的矩阵W，从而实现对矩阵W的压缩。

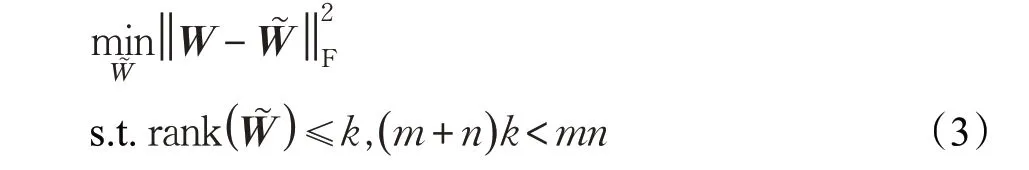
步骤1对矩阵W进行奇异值分解，得到U，S，V。

步骤2令S~表示矩阵S的前k列(k＜r,(m+n)k＜mn)

步骤3将和作为式（4）的初值，最小化式（4），保留优化后的P~和Q~。

步骤4，用来近似W，即用来表示W。

3 基于时间误差的RNN参数压缩

基于循环神经网络的语言模型是一个概率模型，它可表示为[14-16]：

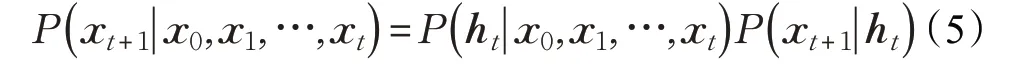
对语言模型的压缩即是对LSTM网络参数的压缩。LSTM网络的定义如下[13]：

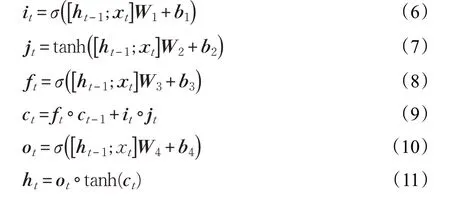
其中，xt和ht表示时刻t网络的输入和状态。it、ft、ot分别表示时刻t网络的三个门限：输入门、遗忘门、输出门。jt表示时刻t网络的输入信息。ct表示时刻t网络的内部状态。W和b分别表示权重矩阵和偏置向量。σ为sigmoid激活函数，tanh表示双曲正切激活函数， 表示矩阵或向量按元素相乘。输入门it决定网络可以输入的信息，遗忘门ft决定网络可以保留的信息，内部状态jt表示网络内部存储的信息，输出门ot决定网络可以输出的信息，ht表示网络的最终输出（网络的状态）。

LSTM模型的参数包含输入门、输入信息、遗忘门、输出门对应的权重矩阵W1、W2、W3、W4，且Wi∈R(embed_size+hidden_size)×hidden_size,i=1,2,3,4

其中embed_size（用es表示）为词向量的维度，hidden_size（用hs表示）为隐层节点个数。

这四个矩阵低秩重构函数如下：

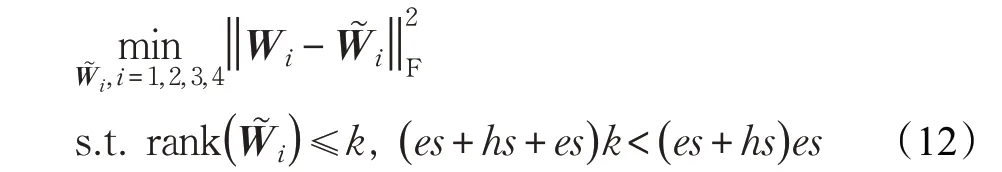
选取满足条件的k，将式（12）按照式（4）的形式表示为：

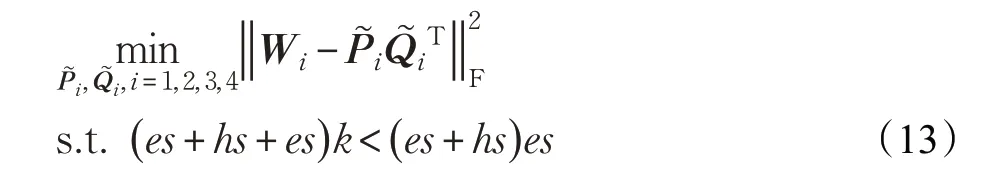
循环神经网络通常和数据时序性有关，随着网络在时间轴上的不断循环传递，长序列信息会随权重的扰动而被破坏[6]。而LSTM的权矩阵通常是满秩的，因此k的选取会小于矩阵Wi的秩，这也会使得Wi和W~i有一定的误差。并且，误差会在时间轴上不断的累计，从而使得模型压缩的性能大幅下降。在对循环神经网络使用低秩重构压缩压缩时，若能考虑时间轴上的误差，则可能会提升压缩后模型的性能。因此，本文提出新的误差重构函数，即在低秩误差重构函数的基础上增加时间项，考虑时间误差来解决这一问题。

误差重构函数为：

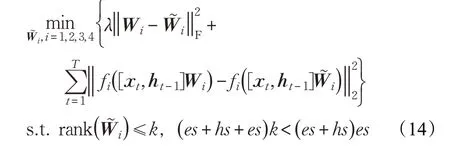
其中，‖‖·2表示向量的2-范数，λ为一个惩罚参数；f是一个非线性函数：i=1,3,4时，f为sigmoid函数；i=2时，f为tanh函数。T为序列数据的长度。xt,ht-1分别表示LSTM网络在时刻t的输入和状态。

式（14）的误差重构函数分为两部分。第一部分与LRRC一样，使矩阵Wi和它的低秩近似W~i之间尽可能接近。第二部分则减小时间轴上的误差。它采用LSTM中的输入激活机制，模拟LSTM网络中的激活功能，使得压缩后的权矩阵尽可能接近。

与低秩重构压缩相比，该误差重构函数以添加时间误差项的形式来减少时间误差，从而提升模型压缩后的性能。

用P~和Q~来表示矩阵W，式（14）又可表示为：

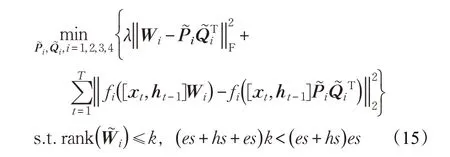
对于满足条件的k，当k越小时，模型压缩的程度越深，模型所需的参数越少。

基于时间误差的低秩重构压缩（Low Rank Reconstruction Compression based on Time-Error，LRRC-TE）算法如下：

输入：训练数据X，整数k，迭代次数N，学习率η；

初始化：n=0；使用X训练好LSTM网络，保留训练好的参数W1、W2、W3、W4和

1.对Wi进行奇异值分解，取Si的前k列得到初始值，i=1,2,3,4；

3.n=n+1；

4.当n＞N时迭代中止。

4 数值实验

为了验证LRRC-TE算法的压缩性能，在IMDB情感分析数据集和Penn Treebank（PTB）数据集进行了对比实验，并探究了惩罚参数对压缩效果的影响。

首先介绍数值实验中用到的相关指标。压缩比（Compression Ratio，CR）的定义如下：

其中，N表示需压缩部分在压缩前的参数个数，N0表示需压缩部分在压缩后的参数个数。压缩比大于1为有效压缩，压缩比越大表示模型待压缩部分的压缩程度越大。

分类模型中准确率（Accuracy）的定义为：

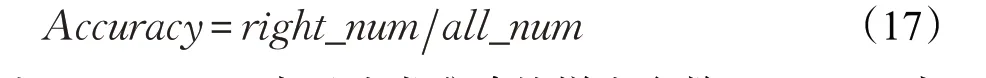
其中，right_num表示分类准确的样本个数，all_num表示所有的样本个数。在同一压缩比下，准确率越高，实验效果越好。

复杂度（Perplexity，PPL）是用来衡量一个语言模型性能高低的一个标准。复杂度越低，代表模型的预测性能越好。它的定义如下：

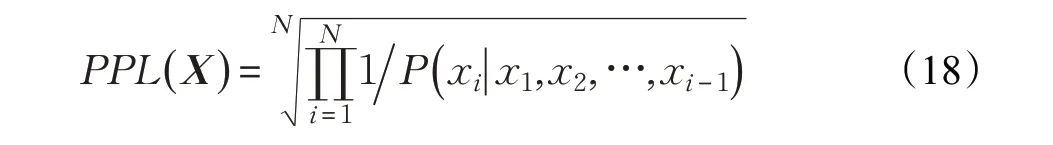
其中X表示文本序列{ }x1,x2,…,xN。实际计算时，采用的公式如下：

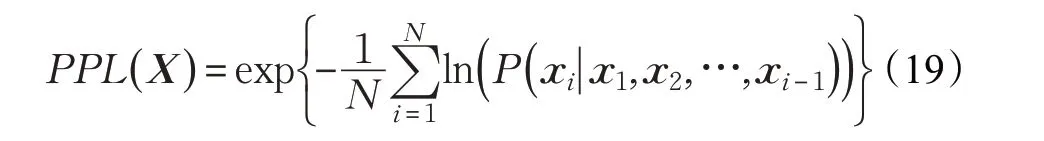
4.1 IMDB数据集文本分类的压缩效果

IMDB情感分析数据集是一个包含5万条电影评论的二分类数据集，正负影评各占一半。本文选取3万条影评（正负影评各占一半）作为训练集，其余作为测试集，在单词级水平上训练LSTM语言模型进行分类。LSTM语言模型的隐层节点设置为128，学习率0.001，词嵌入的维数设置为300，进行多轮训练，选取测试集精度最高的一组实验结果进行模型压缩。测试集分类准确率达0.861。

在使用LSTM对IMDB数据集进行分类时，LSTM网络中的权重矩阵W1、W2、W3、W4，Wi∈R428×128i=1,2,3,4。在对其进行LRRC-TE时，采用Adam算法进行优化，惩罚参数λ=0.5。本实验中压缩比为：

CR=428×128 k(428+128 )

取有效压缩比k≤98，从98逐步递减，比较LRRC-TE和LRRC在不同压缩比下的分类准确率。

实验结果如图1所示。图1中横轴表示压缩比，纵轴表示分类准确率。图中实线和虚线分别表示LRRC和LRRC-TE（惩罚参数λ=0.5）分类准确率随压缩比的变化情况。LRRC-TE分类准确率在不同压缩比下均高于LRRC，特别是在高压缩比的情形下分类准确率远远高于LRRC的结果。当压缩比为50时，LRRC分类的准确率为0.736，而LRRC-TE分类的准确率有0.846，远远高于LRRC，也很接近未压缩时的准确率0.861。从实验结果可得，在IMDB数据集中，即使在高压缩比的情形下，有时间误差的LRRC-TE，保持模型性能的能力优于LRRC。

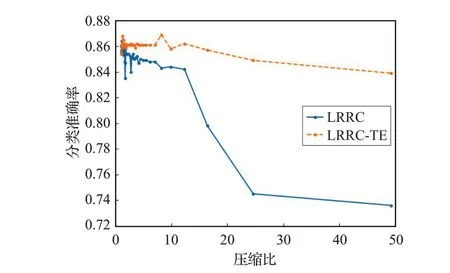
图1 LRRC-TE和LRRC在IMDB数据集上的压缩效果

4.2 PTB数据集文本生成的压缩效果

PTB是一个常用于语言模型的数据集。整个数据集由10 000个不同的单词组成，数据集约包含百万个单词，包含训练集、验证集、测试集。本文建立基于PTB数据集的LSTM单词级语言生成模型。LSTM语言模型的隐层节点设置为128，词嵌入的维数设置为160，进行多轮训练，选取测试集复杂度最低的一组实验结果进行模型压缩，测试集的复杂度为110.263。

对训练好的LSTM语言模型分别进行LRRC和LRRC-TE。在对其进行LRRC-TE时，采用Adam算法进行优化，惩罚参数λ=0.7。本实验中压缩比为：CR=288×128 k(288+128)

其中k的有效范围为k≤88。

实验结果如图2所示。图2中横轴表示压缩比，纵轴表示复杂度。图中实线和虚线分别表示LRRC和LRRC-TE（惩罚参数λ=0.7）复杂度随压缩比的变化情况。从图2可以看到，在同一压缩比下，LRRC-TE的复杂度要低于LRRC，并且随着压缩比的增大，LRRC-TE与LRRC之间复杂度的差距逐渐增大。在PTB数据集上，添加了时间误差的LRRC-TE的压缩效果优于未添加时间误差的LRRC。

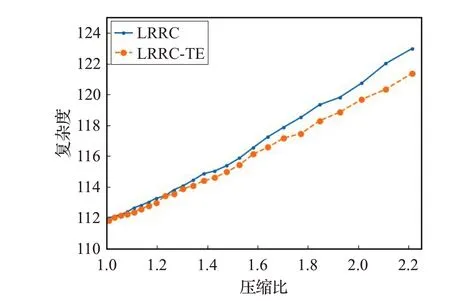
图2 LRRC-TE和LRRC模型在PTB数据集上的压缩效果

4.3 惩罚参数对压缩效果的影响

为了研究惩罚参数对压缩效果的影响，在实验2基础上，对LRRC-TE选取多种惩罚参数进行对比实验。惩罚参数分别选取{0，0.7，1，5}，比较在不同压缩比下的压缩效果。实验结果如图3所示。

图3 不同惩罚参数在PTB数据集上的压缩效果

图3横轴表示压缩比，纵轴表示复杂度。实线表示LRRC在压缩比逐步增大时的复杂度。虚线表示LRRCTE选取不同惩罚参数，复杂度随压缩比的变化情况。

从图3中可得，当λ=0时，即忽略式（15）中的第一项，只保留时间误差重构项。随着压缩比的增大，它的复杂度逐渐地大于其他惩罚参数的情形，甚至大于LRRC。即λ=0时的压缩效果是比较差的。这说明了LRRC-TE中保留第一项（LRRC）的必要性。

此外，从图3中可以看到，随着压缩比的逐步增大，取值较大惩罚参数的压缩效果差于取值较小的惩罚参数。即实际压缩时惩罚参数不宜取值较大。

5 结束语

本文提出了一种新的应用于LSTM的低秩压缩算法，LRRC-TE。LRRC-TE在LRRC的基础上增加时间误差来进行误差重构，减小压缩LSTM引起的在时间轴上的误差。与LRRC相比，在添加了时间误差项后，该压缩算法在IMDB数据集和PTB数据集上表现出更好的压缩性能。下一步考虑将LRRC-TE用于深层LSTM和其他循环神经网络的压缩。