广义共轭余差法的通信避免算法
2020-02-19金之雁林隽民
金之雁,杨 磊,林隽民,王 哲
1.中国气象科学研究院,北京100081
2.英特尔中国有限公司,北京100081
1 引言
广义共轭余差法(Generalized Conjugate Residual method,GCR)[1]是一种用于求解非对称线性方程组的有效算法。中国气象局的新一代“全球区域一体化数值预报模式(Global/Regional Assimilation and PrEdiction System,GRAPES)”[2],其动力框架的核心是亥姆霍兹方程求解器,求解器所采用的就是GCR算法。和其他类似算法一样,GCR算法存在的一个制约可扩展性的问题就是密集的全局通信。随着CPU单节点运算能力的不断提高,这个问题已经成为了制约整个数值模式速率提高的主要瓶颈。
一般来说,算法的开销可以归结为两部分:数据的计算和数据的移动。其中数据的移动包括节点内部的移动和节点间通过网络的移动。要减少这种密集的数据移动带来的开销,加州大学伯克利分校的Demmel教授最早于2007年提出了通信避免(Communication Avoiding,CA)算法[3]。CA算法的思路是:构造能包含迭代过程中的所有长向量的Krylov子空间,利用短向量的迭代替代长向量的迭代,进而避免在迭代过程中进行通信。该思路具体应用于对不同的算法的改造,会产生相应的不同的CA算法。目前针对GCR算法,相关工作仍是空白。
数值预报模式的运算速率是提高预报分辨率的客观前提,“神威太湖之光”、“曙光派”等高性能计算集群的部署已经使GCR算法中的全局通信成为提升GRAPES模式整体速率的最大瓶颈。为此,本文借鉴Demmel教授提出的思路,首创性地对GCR算法进行CA改造,提出CA-GCR算法。新算法的通信次数较之原算法降低了一个数量级,同时,计算量也有一定减少。并且在中国气象局最新部署的“曙光派”计算集群上进行了大规模测试(最大规模16 384进程),在可扩展性(本文中所有“可扩展性”均指“强可扩展性”)和运算速率上表现出了相对于原算法巨大的优势,最高达到原算法3倍的加速比。
2 相关工作
CA算法由Demmel教授提出,之后又由其本人及学生具体应用于共轭梯度法、广义最小剩余法等经典算法的改造,多数表现出了对通信量和计算量的双重作用,即同时减少两者的开销。Demmel教授的学生Grigori于2008年将CA算法应用于一般高斯消元法[4];Demmel于2010年对LU分解进行CA优化[5];Hoemmen于2010年对广义最小剩余法进行CA优化[6];Maryam于2013年在图形处理单元方面实践CA算法[7]……教授及其学生的研究成果现已涵盖多数主流算法,但GCR算法的相关工作仍是空白,目前国内外都没有相应方案。
3 算法描述
3.1 原始算法
2008年曹建文等人对GRAPES模式中亥姆霍兹方程的系数矩阵进行ILU分解,形成了“带预条件的广义共轭余差法”(Preconditioned Generalized Conjugate Residual method,P-GCR)[8],目前已应用于业务运行。在本文中,以该算法为原始算法。其具体算法如下:
算法1带预条件的广义共轭余差法(P-GCR)
待解方程组Ax=b,解的初猜值x0,
余差ri, 下降方向向量pi,
预条件矩阵M-1,重启间隔s,
系数αk,βkj
x0,r0=b-Ax0,z0=M-1r0,p0=z0
while not converged do
1.for k=0:s-1,do
2.αk=rTkApk/pTkATApk
3.xk+1=xk+αkpk
4.rk+1=rk-αkApk⇔zk+1=zk-αkM-1Apk
if converged,exit
5.βjk=-ATApj/pTjATApj(j=0,1,…,k)
6.pk+1=zk+1+
7.end for
8.r0=rs,p0=ps
end while
算法1中,A、M-1是n阶方阵(n的大小取决于具体算例),x、r、p、z是长度为n的向量。
算法1中第2步的pTkATApk和第5步的ATApj分别是一次长向量点乘计算。长向量的点乘需要进行并行化计算,各个进程计算结果进行全局范围的求和,由此要各产生一次全局通信,因此每s步迭代中(本文中取s=10),将进行2×s次全局通信。并且通信间存在严格的依赖关系,无法通过合并而减少。
3.2 CA-P-GCR算法及推导
CA算法的基本思路:
(1)证明迭代过程中的长向量都存在于同一个Krylov子空间中,因此可以用空间下一组坐标(短向量)来代替长向量。
(2)把短向量代入原始算法,用短向量的迭代取代相应长向量的迭代,以此实现迭代过程中的通信避免。
CA-P-GCR算法的推导:
定义Krylov子空间
Ks+1(A,v)=span{v,Av,A2v,…,Asv}(v为任意向量)
在算法1中,当k=0时,由第3步得:
x1-x0∈K1(M-1A,p0)
由第4、6步得:
z1∈K2(M-1A,p0),
p1∈K2(M-1A,p0)
同理,当k=s时,有结论:

选取适当向量建立基
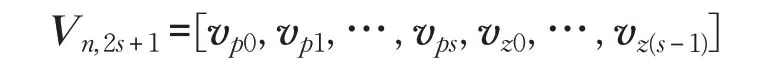
其中,选取vp0=p0,vz0=z0。
vpi和vzi由下式产生:
vp(z)i=αM-1Avp(z)(i-1)+βvp(z)(i-1)+γvp(z)(i-2)
其中i≥2。
α、β、γ的值依所采用的不同基而定,较复杂的基(如切比雪夫基、牛顿基)之间具有更低的相关性,可以支持更高的重启间隔s,但同时在计算α、β、γ时也会带来一定的计算量。根据实际情况,在本例中,选取最简单的单项式基,即:α=1,β=0,γ=0
根据结论式(1),可以设:

其中,短向量mi,ni,li的长度为2s+1。
将以上设定代入原算法中,代入第2步得:
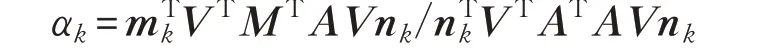
代入第5步得:

设有Gram矩阵:

于是:
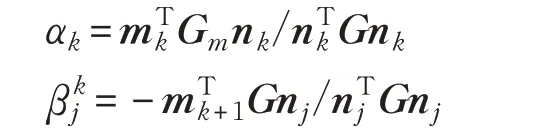
其中G、Gm均为2s+1阶方阵。
由第3步得:

根据生成矩阵A的气象学原理,当p0≠z0时,V的各分量线性无关,方程有唯一零解;当p0=z0时,V的秩为s+1,短向量的相应坐标也保持相等,方程相当于一个s+1列方程,同样只有唯一零解,因此有:
同理,由第6步得:


由第4步得:

设有换基矩阵T满足M-1AV=VT,得:
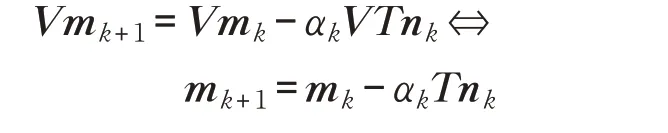
其中,换基矩阵T在单项式基下为:

其广义形式根据公式vp(z)i=αM-1Avp(z)(i-1)+βvp(z)(i-1)+γvp(z)(i-2)而定。
经过这样的替代,在迭代过程中,不再有长向量出现(只在计算Gram矩阵过程中出现长向量),于是,“通信避免的带预条件的广义共轭余差法”(Communication Avoiding Preconditioned Generalized Conjugate Residual method,CA-P-GCR,以下简称CA算法)描述如下:
算法2通信避免的带预条件的广义共轭余差法
x0,r0=b-Ax0,z0=M-1r0,p0=z0
while not converged do
1.Calculate V=[p0,M-1Ap0,(M-1A)2p0,…,(M-1A)sp0,z0,M-1Az0,…,(M-1A)s-1z0]
2.Let G=VTATAV Gm=VTMTAV
3.m0=[0s+1,1,0s-1]Tn0=[1,02s]Tl0=[02s+1]T
4.for k=0:s-1,do
5.αk=mTkGmnk/nTkGnk
6.lk+1=lk+αknk
7.mk+1=mk-αkTnk
8.βjk=-Gnj/nTjGnj
9.nk+1=mk+1+
10.end for
11.zs=Vms,ps=Vns,xs=x0+Vls
12.z0=zs,p0=ps
end while
算法2中,0s表示s个实数0组成的行向量,只有在第2步与第3步之间进行一次全局通信,即每s次迭代进行一次全局通信。
为减少计算量,本文又对算法2中第11、12步修改如下:
11.xs=x0+Vls
12.r0=b-Axs,z0=M-1r0,p0=z0
修改前,第12步新生成的z0≠p0,其后的第1、2步的计算过程中要对z0、p0分别进行稀疏矩阵向量乘、点乘。修改后,第12步新生成的z0=p0,其优点是大幅减少了后续第1、2步的计算量。相应的代价是总迭代次数会有小幅增加,因为这样修改之后的算法和原算法在数学上已经不再等价。但是由于CA算法的迭代次数只能是s的整数倍,实际运行后发现,实际的迭代次数并没有因为以上修改而增加。
3.3 解的唯一性与正确性
待解方程Ax=b的解的唯一性由A、b的属性决定,而A、b的生成依赖于相关的气象学原理。根据相关气象学原理可以确定,待解方程的解存在且唯一。
新算法与旧算法求得的方程解并不完全一致,其原因至少包括以下2条:
(1)两种算法迭代次数不同。
(2)算法2中对第11、12步的修改。
其中,原因(1)在所有CA类算法中普遍存在。但是模式动力框架对方程求解器模块的要求,并不是不同算法解的一致,而是仅仅要求收敛。后续的动力框架部分和物理过程部分的计算,也都仅以方程求解器的收敛为前提。
3.4 新旧算法计算量对比
对比原算法和CA-P-GCR算法,计算量对比如表1。

表1 新旧算法的计算量
对比发现:每s步迭代(即每个restart周期),CA-P-GCR中全局通信的次数减少为原算法的1/(2×s)。稀疏矩阵向量乘减少了约一半,点乘计算量增加s次。按照以往测试结果,稀疏矩阵向量乘的计算量远高于点乘。因此预测CA算法将在计算、通信两方面同时优于原算法。同时,相比原算法,计算部分更加集中,存在进行访存优化、提高计算访存比的潜力。
4 数值实验
4.1 算例信息
本测试的测试对象是中国气象局的新一代“全球区域一体化数值预报模式(GRAPES)”,其动力框架的核心是求解亥姆霍兹方程Ax=b,本测试共运行288步,每步进行1次方程求解,每次求解过程中,A、b不变,x初猜值继承上一次的最终结果(第一次初猜值取0向量)。本测试采用0.05°水平分辨率的全球算例,垂直层数60层,时间步长150 s,物理过程关闭。A是1.56×109阶方阵,x、b是长度为1.56×109的向量。因为A、x、b以及迭代过程中出现的z、p、r规模较大,所以计算时按节点分别存储。A是稀疏矩阵,每一行中有19个非0元。
4.2 计算集群信息
本测试所用计算集群是中国气象局2018年部署的“曙光-派”计算集群,采用Intel的SKL Gold 6142处理器,主频2.6 GHz,32核/节点,每个核心运行1个进程,纯MPI并行。每节点内存为192 GB的DDR4内存,操作系统RHEL 7.4,编译器Intel PSXE 2017u2。
5 实验结果
5.1 收敛速率对比
测试中,每种算法各进行方程求解288次,每次求解的迭代次数各不相同。经统计得:CA算法平均迭代次数为34次,原算法平均迭代次数为28次。现以4 096进程下一次典型求解过程为例,如图1所示。
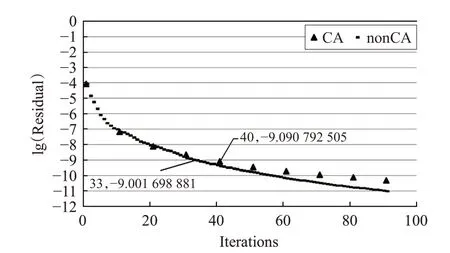
图1 新旧算法收敛速率
说明:本文以r0全体元素的平方和作为残差(由于三维空间格点总数不变,因此没有进行平均、开方运算),收敛阈值定为1.0×10-9,图1中纵坐标为残差的常用对数。由图1可知,本次求解过程中,随着迭代次数的增加,CA算法的收敛速率略慢于原算法。同时,CA算法的迭代次数为不连续的、10的整数倍。原算法达到收敛阈值的迭代次数是33次,CA算法达到收敛阈值的次数是40次。
在整个测试中,CA算法的平均迭代次数高于原算法的原因主要有以下3条:
(1)CA算法的迭代次数只能是s的整数倍(本文中s全部取10)。
(2)所有CA算法由于基的条件数的限制,都存在最高收敛精度降低,收敛速率小幅变慢的问题。Carson于2014年针对各种“通信避免算法”中出现的这类问题进行了详细分析,并给出了“余差替代”解决方案[9]。本文所提出的算法也存在相同的问题,但由于“余差替代”方案开销较大,因此没有采纳。
(3)前文中修改第12步,改变生成新的z0、p0的方法,使得z0、p0相等。这就改变了基的条件数,进一步减慢了收敛速率。
由于要兼顾通信量和计算量,s的选取受到一定限制,使得以上(2)、(3)两条的效果被(1)所覆盖,因此(2)、(3)两条并没有实质上增加总的迭代次数[10]。
5.2 总时间对比
本测试并行规模从2 048进程到16 384进程,GRAPES模式的整体运行时间(图2)和亥姆霍兹方程求解器的运行时间及加速比(图3)如下所示。

图2 新旧算法的模式总运行用时及加速比

图3 新旧算法的求解器运行用时及加速比
对比图2和图3可知,方程求解器的时间消耗占据了整个数值模式的重要部分(从42%到65%)。求解器之外的部分并没有做修改,因此差别不明显。求解器算法的优化,导致了模式整体运行速率最高1.64倍的加速比(相对于同规模下的原算法)[11]。
由表1可知,CA算法在计算量、通信量上都优于原算法,从图3也可知从2 048进程到16 384进程上,CA算法的用时都少于原算法,并且这种优势随着并行规模扩展而扩大。从图3的加速比可以看出,当规模扩展到16 384进程时,CA算法的加速比达到了原算法的3倍[12]。对比新旧算法求解器部分的可扩展性,两种算法在规模较小时都表现出良好的可扩展性,当规模较大时,CA算法仍然保持可扩展性,而原算法随规模扩展而速度降低。
5.3 主要计算、通信部分时间对比
并行规模较小时,计算开销(包括稀疏矩阵向量乘、点乘)占据主要部分,其用时远高于通信。并且随着规模的扩展,计算部分的加速呈现“超线性”[13],例如:4 096进程的并行规模是2 048进程的2倍,但稀疏矩阵向量乘用时仅为2 048进程的1/4~1/3。推测其主要原因是规模较小情况下,内存压力较大,导致访存命中率偏低。随着并行规模扩大,通信用时逐渐占据了主要部分,CA算法的优势主要体现在通信上,16 384进程下,原算法的通信开销已经远远超过了计算开销。
另外,对比图2、图4,随着并行规模的扩展,原算法的全局通信用时最高占据了模式整体运行时间的50%,由此说明了通信避免的必要性。
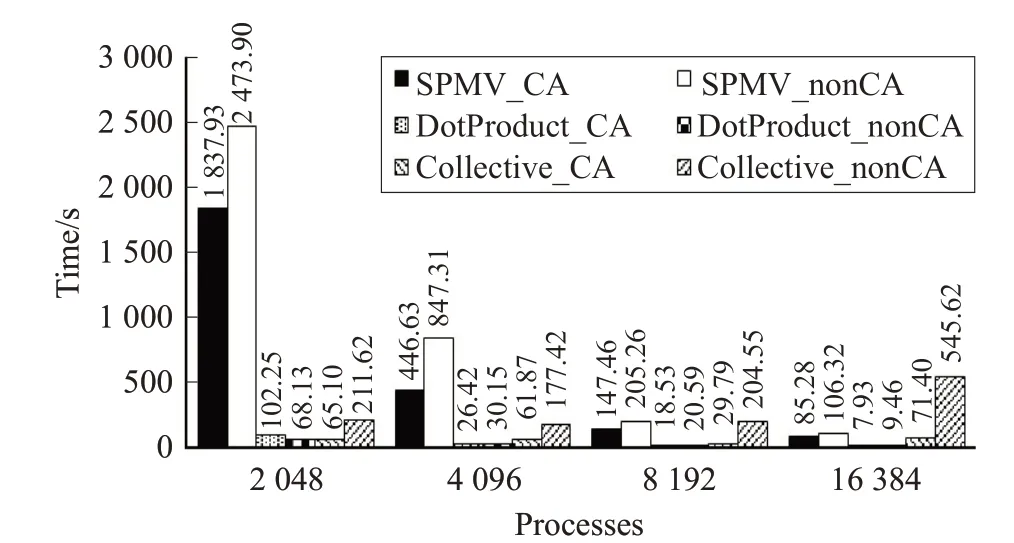
图4 新旧算法的主要计算及通信用时
6 结论
GRAPES模式使用原算法的亥姆霍兹方程求解器受限于全局通信,其扩展能力止步于8 192进程。本文通过通信避免算法改造,以小幅降低收敛速率为代价,同时改善了求解器的运行速率和扩展能力,在16 384规模平台上的实验显示出3倍于原算法的加速效果[14]。
综合以上结果可知:CA算法可以极大地改善方程求解器的可扩展性,并且减少运算、通信的时间开销,在各种计算规模下都有着相比于原算法明显的优势[15]。在较小规模下的优势主要来源于计算的减少,在较大规模下的优势主要来源于全局通信的减少。同时,会导致收敛速率的小幅降低。
