基于聚类和用户偏好的协同过滤推荐算法

王卫红，曾英杰

浙江工业大学 计算机科学与技术学院，杭州310023

1 引言

随着社会信息化的发展，互联网中的数据飞速增长，为了帮助用户在海量数据中找到满足用户需求的数据，大量的研究者和学者对相关方案进行了探索，由此便有了推荐技术的发展。

推荐算法主要有基于协同过滤的推荐[1]、基于内容的推荐[2]和基于关联规则的推荐[3]。其中，基于协同过滤的推荐是众多学者研究的一种主流的推荐算法，现实中应用也比较广泛。

协同过滤算法中需要计算相似度，通常使用Pearson相关性相似度或余弦相似度作为度量标准。协同过滤算法的基本假设是：如果某用户A在一个项目上与另一个用户B具有相同的评价，那么用户A对另一个项目的评价也可能与用户B相同。由于协同过滤推荐算法使用的评分数据通常非常稀疏，导致协同过滤推荐算法的推荐性能显着下降，为了解决这个问题，文献[4]中总结了深度学习的最新进展（基于CF）提出协同深度学习（CDL）。在文献[5]中，作者也结合深度学习提出了神经协同过滤方法。以上结合了深度学习的方法虽然改善了推荐效果，但是深度学习训练神经网络模型需要大量的时间开销。为了解决协同过滤推荐算法中评分数据的稀疏性和可扩展性差的问题，许多研究者提出了填充稀疏数据集、矩阵分解、降维或聚类[6-8]等方法。矩阵分解是推荐系统最有效的方法之一，用于推荐任务的矩阵分解最先由Simon Funk3在Netflix竞赛中设计用于评级预测。后来的研究改进了矩阵分解并提出了许多变种[9-10]。Slope One算法是由Lemire等人提出的一种基于内存的协同过滤推荐算法[11-12]。文献[13]中提出了一种基于用户聚类与Slope One填充的协同推荐算法，该算法可以降低数据的稀疏性，提高推荐精度。由于用户评分矩阵具有很高的稀疏性，而有用的评分信息只包含与目标用户相关联的评分，为了避免使用整个用户评分矩阵进行学习，文献[14]中提出一种近邻矩阵分解算法，该算法将用户近邻与项目近邻评分信息融合成一个近邻评分矩阵，然后在这个新的近邻评分矩阵中预测目标用户对目标项目的评分信息。文献[15]中，作者通过矩阵分解对原始数据进行数据填充和降维，并通过K-means聚类算法对用户和项目分别进行聚类以改善最终的推荐效果。为了改善推荐效果，也有研究者在计算用户相似度的时候做了改进[16-17]。

针对上述相关研究中存在的问题，本文提出了一种基于聚类和用户偏好的协同过滤推荐算法，该算法为了提高用户相似度精度，以用户对项目类型的平均评分作为度量标准引入了用户对项目类型的偏好，并基于用户自身属性加入相似性权重；然后用使用Weighted Slope One算法填充评分矩阵中的未评分项以降低其稀疏性；接着通过融入密度和距离优化初始聚类中心的K-means算法聚类填充后的评分数据中的用户；最后在聚类后的数据集中使用传统的协同过滤推荐算法生成推荐结果。该算法在电影推荐、图书推荐、音乐推荐场景下尤为适用。

2 相关工作

传统的基于用户的协同过滤推荐算法通过汇总一些类似用户先前给予该项目的评级来预测用户对目标项目的评级。主要步骤有：首先把评分数据转化为m行n列的用户-项目评分矩阵，记为：Rm,n；然后根据评分矩阵计算每个用户与其他所有用户之间的相似度，并按照相似度获得目标用户的前N个最近邻用户集Nu；最后通过目标用户u最近邻用户集Nu中的用户对目标项目i的评分预测目标用户u对目标项目i的评分。

预测评分Pu,i计算公式表示如下：

2.1 用户相似度计算

2.1.1 余弦相似度

余弦相似度通过用户特征向量的夹角余弦值sim(u,v)来衡量用户之间的相似程度[18]，假设有用户u和用户v，则用户u和用户v的余弦相似度sim(u,v)满足：-1≤sim(u,v)≤1,sim(u,v)越大则说明用户u和用户v越相似，余弦相似度sim(u,v)用公式（2）表示：

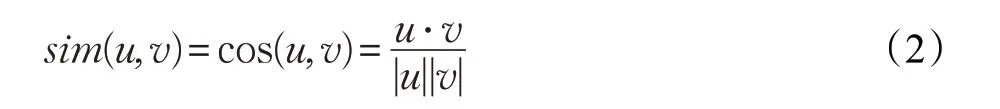
2.1.2 基于Pearson相关系数的相似度

皮尔森相关系数法是使用的非常多的一种相似度计算方法[19]。相对于余弦相似度，Pearson相关系数相似度对变量进行了均值化（或去中心化）处理，降低了变量个体的数值差异对变量间相似度的影响，本文采用Pearson相关系数计算用户间的相似度。假设有用户u和用户v，则他们共同评分的项目用集合S表示，ru,i和rv,i分别表示用户u和用户v对项目i的评分，和分别表示用户u和用户v对各自已评分项目的平均评分，则用户u和用户v之间的相似度sim(u,v)可以表示为公式（3）：

2.2 Weighted Slope One算法

由于协同过滤推荐算法中使用的用户评分数据具有很高的稀疏性，使用Weighted Slope One算法填充用户评分数据中用户未评分的项目可以降低评分数据稀疏性。

定义用户的评分矩阵为Rm,n，假设有用户u，其已评分项目为i，Iu为用户u所有已评分的项目集合，即i∈Iu，用户u待预测评分的项目为j。首先计算项目i项目j之间的评分偏差disi,j，计算公式如下：

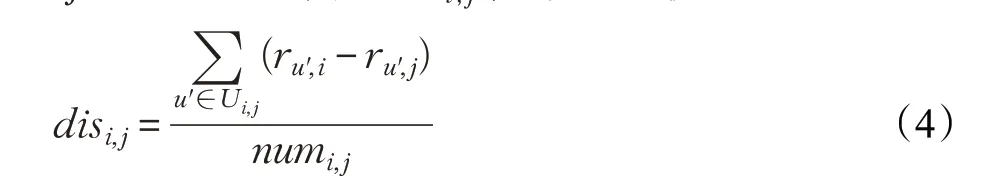
其中Ui,j为对项目i和项目j都评过分的用户集合，u′是集合Ui,j中的用户，ru′,i为用户u′对项目i的评分，ru′,j为用户u′对项目j的评分，numi,j为集合Ui,j中元素的数量。

然后根据评分偏差disi,j和目标用户u对项目i的评分ru,i计算目标用户u对项目j的预测评分preu,j，计算公式如下：

2.3 K-means算法

K-means算法根据相似性原则将具有较高相似度的数据对象划分至同一类簇，一般采用欧式距离作为数据对象之间相似性的度量标准。假设有数据集D，其中的每个数据对象有n维，则两个数据对象之间的欧式距离的d(x,y)可表示如下：

传统的K-means算法随机选择初始簇心，通过相似度计算，把数据集中的数据样本与最近的初始中心归为一类，不断重复这一过程，直到各个初始中心在某个精度范围内不变。具体算法步骤如下：

（1）随机选取K个中心点。

（2）遍历所有数据对象，计算所有数据对象到中心点的距离，并将每个数据对象划分到距离最近的中心点中。

（3）计算每个聚类簇的平均值，并作为新的中心点。

（4）不断迭代，重复步骤（2）和步骤（3），直到K个中心点不再变化或达到最大迭代次数。

2.4 融入密度和距离优化K-means初始簇心

K-means算法虽然实现时简单方便但也存在一些缺点。例如，聚类的数量K是根据人的经验判断的，因此给出一个合理的K值会比较困难。此外，K-means算法对初始簇心的选择也是随机的，每次聚类选取的初始簇心不同会导致不同的聚类效果，并且在聚类时如果选择了孤立点作为聚类中心，则无法达到较好的聚类效果。

针对以上K-means算法存在的缺点，文中在应用K-means算法处理数据时结合密度和距离对初始聚类中心进行优化[20]。在选取聚类初始簇心时，首先通过贪心策略寻找数据对象的邻域半径和密度较大的簇；然后不断选取密度较大且距离最远的簇作为临时初始簇，并将初始簇中支持度最高的核心数据对象作为初始簇的中心。具体步骤如下：

输入：数据集的n个数据对象；聚类个数K；形成初始簇的最大簇内个数Cmax，最小支持度minPts。

输出：K个作为初始簇中心的核心数据对象。

（1）根据公式（6）计算数据集中数据对象两两间的欧式距离dis。

（2）根据最小支持度minPts找出所有核心数据对象，并按密度排序。

（3）在步骤（2）得到的核心对象中选取密度最大的一个数据对象和相距该数据对象最远的一个数据对象作为初始簇心。

（4）在剩余的核心数据对象中，选取密度次大并且距离已选为初始簇心的数据对象最远的数据对象作为初始簇心。

（5）重复步骤（4），直至选取K个初始簇心。

通过以上步骤选取的初始簇密度很高，且初始簇心相距较远，聚类效果稳定可靠。

3 本文算法

协同过滤算法使用评分数据作为学习的数据源，评分数据中的每条数据主要由用户、项目和评分三部分组成。本文算法通过Weighted Slope One算法填充评分矩阵中的未评分项以降低评分数据的稀疏性；引入了以用户对项目类型的平均评分为衡量标准的用户偏好；使用K-means聚类，通过对用户聚类缩减了目标用户的最近邻用户计算范围。

假设有用户集合U={u1,u2,…,um}，项目集合I={i1,i2,…,in}，则评分矩阵为Rm,n，其中ru′,i为用户u对项目i的评分，评分矩阵如公式（7）：

其中，对于每个用户则有如表1所示的用户-项目评分。

表1 用户-项目评分

假设已知每个项目的类别或属性，则用户在对项目评分时也隐式地给项目的类别评了分。对于用户u，具有已评分项目集合Iu，每个项目i具有一个或多个类别Tt(t=1,2,…,k)。则用户u对类别Tt的平均评分ru,t可表示如下：

其中若项目i具有类别t，则it=1，否则it=0。numu,t表示用户u已评分项目具有类别t的项目总数。根据公式（8）提取用户对类别的平均评分，得到表2的用户-类别评分表。

表2 用户-类别评分

由于每个用户的喜好不同，则对于每一个项目类别的评分也应该不同，甚至会出现某个用户对某一类别从未有过评分。基于这上述假设，本文将用户对类别的评分添加到评分矩阵。添加了用户类别评分后，降低了数据的稀疏性，增加了每个用户间评分向量的差异，在计算用户相似度时能够提高精度。加入用户类型评分后，评分矩阵可由公式（9）表示：

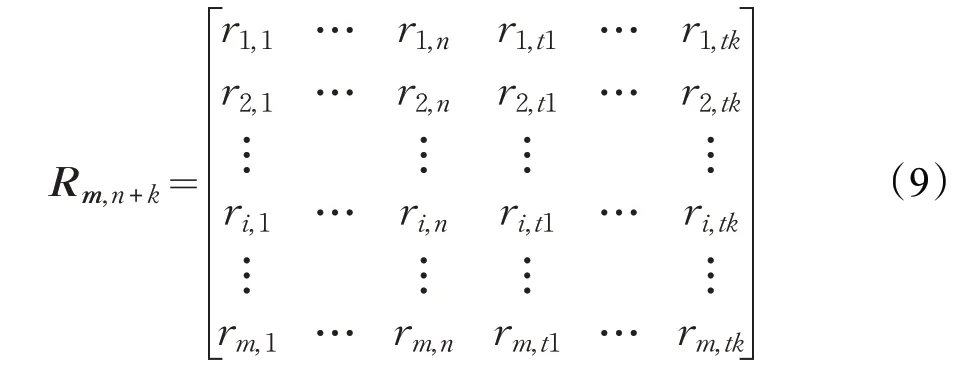
同时，由于不同年龄段、不同性别和不同职业的用户对项目类别的偏好也应该不同，基于这一假设，本文通过用户的年龄、性别和职业这些自身属性，计算用户间的相似度simo(u,v)。用户属性表可表示如表3。

表3 用户属性和职业-类别评分

为了体现不同职业的类型偏好，本文算法引入职业对类型的平均评分。在实际应用场景中，用户注册时会填写自身的一些信息，这些信息会存到数据库中，因此可以从数据库抽取用户的属性。

如表3所示。表中1代表男性；2代表女性，最终形成一个基于用户自身属性的向量，并基于该向量通过公式（3）计算用户间的相似度simo(u,v)，则最终预测评分时使用的相似度sim(u,v)可表示为sim(u,v)=simr(u,v)×simo(u,v)，其中simr(u,v)为基于用户-项目评分数据计算得到的用户相似度。

本文算法描述如下：

输入：用户-项目评分矩阵Rm,n，聚类个数K；

输出：N个推荐项目。

（1）通过用户-项目评分矩阵Rm,n计算得出用户-类别评分矩阵R1，并合并两个评分矩阵，得到评分矩阵R2。

（2）使用公式（5）填充评分矩阵中用户未评分的项，降低评分矩阵的稀疏性，得到评分矩阵R3。

（3）以评分矩阵R3为聚类输入数据，找出融入密度和距离的K-means聚类初始簇心，并通过这些初始簇心结合K-means算法将用户聚类得到K个簇。

（4）使用公式（6）计算目标用户u和K个簇心之间的距离，并把目标用户u添加到距离最近的簇中。

（5）在目标用户u所在的簇中，根据公式（3）计算目标用户u与簇中其他用户的相似度sim(u,v)，得到用户u的最近邻居集Nu。

（6）根据目标用户u最近邻居集Nu中的用户对项目的评分，使用公式（1）计算目标用户u对其未评分项目的预测评分，并把预测评分最高的前N个未评分项目推荐给目标用户u。

本文的算法流程图如图1所示。

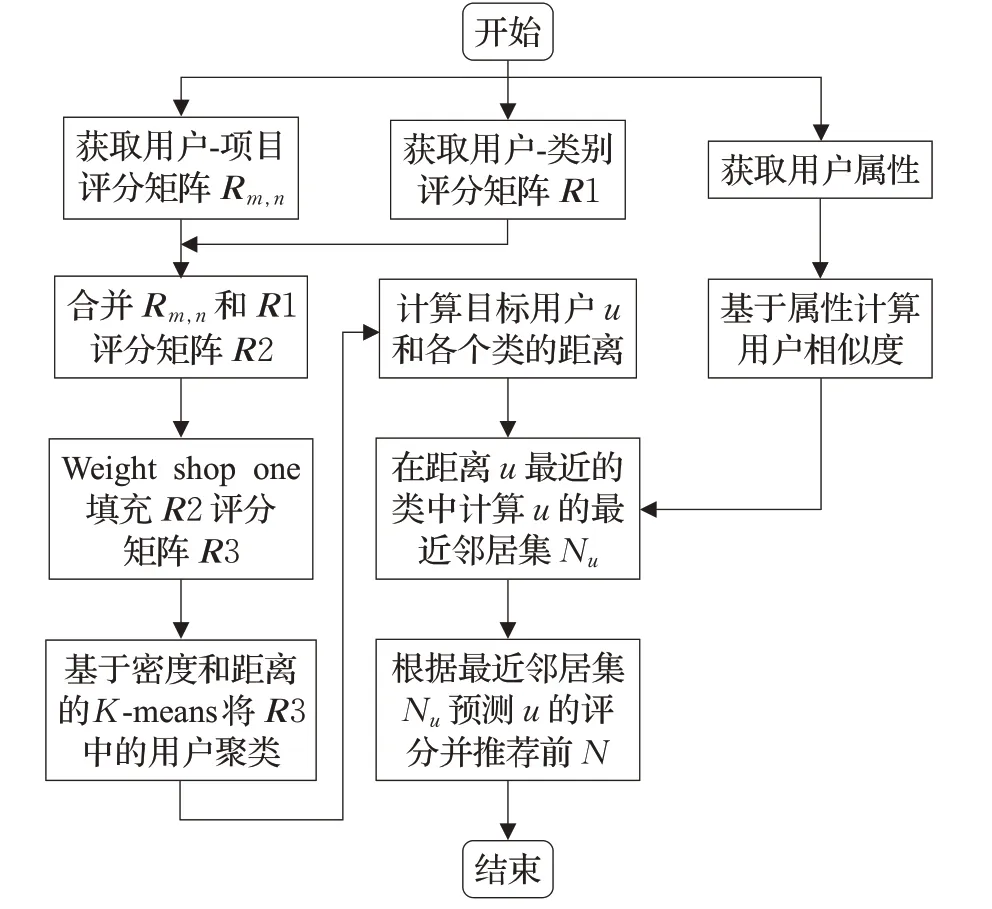
图1 本文算法流程图

如图1所示，获取用户-项目评分矩阵Rm,n、获取用户-类别评分矩阵R1和计算基于用户自身属性的相似度这三个步骤相对独立，因此这三个步骤可以并行计算。

本文算法的时间复杂度主要体现在聚类、数据填充和计算用户相似度这几个步骤中，其中最大的时间复杂度为O(n2)，n是用户的数量。在空间复杂度方面，算法输入的评分数据需要O(i·n)，其中i是用户平均评分个数，n是用户的数量，另外算法中需要保存用户相似矩阵，其空间复杂度为O(n2)。本文算法的时间复杂度和空间复杂度主要受用户数量影响，通过聚类用户可以缩小相似用户的计算范围，在后续的推荐过程中可以有效降低时间复杂度和空间复杂度。

4 实验

4.1 实验数据集与评估标准

实验中采用美国明尼苏达大学GroupLens项目组提供的MovieLens数据集对本文算法的性能进行测试。其中包括100 KB、1 MB、10 MB三个规模的数据集。本文采用100 KB的数据集进行实验，其中包括943个用户对1 682部电影的10万条评分数据，电影类别总共有18种，评分标准为1到5之间的整数。数据集中用户对某一电影的评分值越大说明用户越喜欢这部电影。为了评估算法性能，将数据集的80%作为训练集，其余的20%作为测试集。

实验采用平均绝对偏差（Mean Absolute Error，MAE）和均方误差（Root Mean Square Error，RMSE）来评估推荐效果。MAE和RMSE是推荐算法中常用的评价指标，两个指标都是越小则推荐效果越好。MAE通过计算训练集中的预测评分和测试集中真实评分之间的平均绝对偏差来度量评分预测的准确性。假设用户u对N个项目的预测评分为P={p1,p2,…,pn}，对应的真实评分为R={r1,r2,…,rn}，则MAE和RMSE的计算公式如下：

4.2 实验结果与分析

实验中通过对初始评分数据中的未评分项进行填充，降低了评分矩阵的稀疏性，并引入了用户对电影类型的评分和用户自身的属性；然后采用基于密度和距离优化初始簇心的K-means算法对用户进行聚类，最后在目标用户所在簇中用传统的基于用户的协同过滤推荐算法得出最终的推荐结果。实验中将基于用户的协同过滤推荐算法（UBCF）、基于K-means聚类的协同过滤推荐算法（K-meansUBCF）、基于Slop One填充稀疏矩阵的协同过滤（FUBCF）、基于用户聚类和填充稀疏矩阵的推荐算法（CFUBCF）与本文中的算法进行了对比。通过实验取最佳聚类簇数为7，设定目标用户的最近邻居个数从5递增到50，递增的间隔为5，得出的实验结果如图2和图3所示。

由图2和图3可知，实验中所用的UBCF、K-means UBCF、CFUICF和本文所提出的算法的MAE值都会随着目标用户最近邻居个数的增加而降低并逐渐趋于一个稳定值。本文所提出的算法在不同最近邻居个数下的MAE值都明显低于其他两种算法。以最近邻居个数30为例，UBCF的MAE值为0.763，而本文所提出的算法的MAE值为0.727，推荐效果提升了3.6%。

图2 MAE对比图

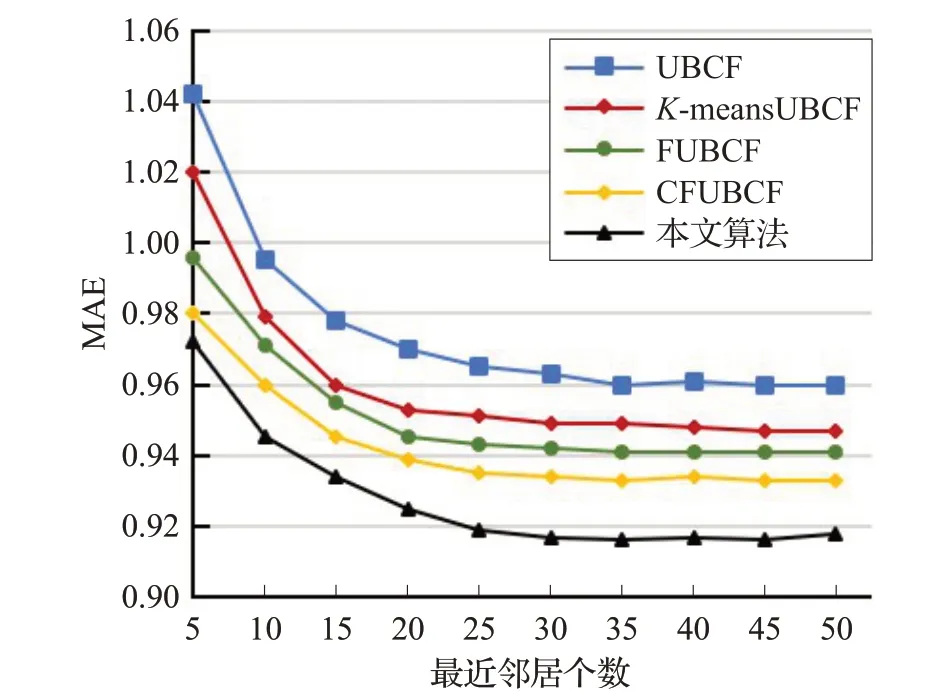
图3 RMSE对比图

5 结束语

本文算法通过引入以用户对项目类型的平均评分和用户自身属性作为衡量标准的用户偏好，提升了计算用户相似度时的准确度，使用Weighted Slope One算法填充评分数据中的未评分项以降低评分数据的稀疏性，并通过融入密度和距离优化初始聚类中心的K-means算法聚类填充后的评分数据中的用户，提升了算法的可拓展性；最后在聚类后的数据集中使用传统的协同过滤推荐算法生成目标用户的推荐结果。通过使用MovieLens100K数据集实验证明，本文提出的算法提升了推荐精度。由于本文的算法主要使用在离线情景下，在实际推荐系统中，实时推荐也尤为重要，因此下一步的工作是将该算法与实时计算框架结合，并融入时间因子，在实时推荐方向展开研究。