融入K-核迭代因子的重叠社区发现算法

赵 亮，朱征宇

重庆大学 计算机学院，重庆400044

1 引言

现实世界很多复杂的相互作用的关系往往被抽象成复杂网络来表示，例如互联网环境下的社交网络、电子商务、流行病传播学中的预防控制过程、生物学网络中蛋白质组织结构等。而社区作为复杂网络中广泛存在的结构，通过研究社区可以很好地了解和认识复杂网络的结构和功能。社区并没有一个严格意义上的定义，较为广泛接受的是Newman和Gievan提出的“同一社区内的点与点之间的连接更紧密，不同社区之间点的连接更稀疏[1]”。

在现实世界的复杂网络中，存在一些节点同时属于不同的社区，这便是所谓的重叠社区结构[2]。CPM算法[3]是早期能够发现重叠社区的发现算法，算法通过找出极大完全子图来发现重叠社区；COPRA算法[4]采用标签传播的方式来发现重叠社区，初始化时，每个节点被赋予一个唯一标签，通过无数次迭代更新节点标签及其隶属度，最终具有相同标签的节点同属一个社区，其中具有多个标签的节点为重叠节点；CRD-LPA算法[5]通过节点重要性在标签传播阶段选择标签，提高了算法的稳定性。LBSA算法[6]和OCDEDC算法[7]通过网络中边的特性来发现重叠社区。Lancichinetti等人[8]提出基于局部扩展的重叠社区发现算法（LFM），该算法通过随机选择种子节点，不断加入适应度增益最大的节点来组成局部社区，尽管LFM算法能够发现重叠社区和社区间的层次关系，但存在结果不稳定、社区漂移等问题；文献[9]采用最大团策略进行社区的扩展合并，获得重叠社区。

本文针对现有的局部扩展类算法的结果不稳定、社区漂移等问题，提出基于K-核迭代因子和社区隶属度的重叠社区发现算法（KIMDOC），其基本思想是：首先引用迭代的思想对K-核分解算法[10]进行改进，得到K-核迭代因子[11]，然后将K-核迭代因子与节点密度值相结合得到节点影响力，利用节点影响力找出种子节点；再通过节点影响力计算得到节点的社区隶属度，最后根据社区隶属度从种子节点局部扩展至整个网络，从而发现网络中的重叠社区。

2 相关工作

2.1 LFM算法

LFM算法是局部扩展类重叠社区发现算法的经典算法，大多数局部扩展类算法都是以此算法为基础进行改进的，该算法通过引入适应度函数来衡量社区C的紧密程度，计算社区C邻接点的适应度并将适应度最大的邻接点加入到社区C中，重新计算社区C中各个点的适应度并去除适应度小于零的节点，当社区C不再变化时扩展终止。适应度计算方式如式（1）所示：

（1）随机选择一个未加入社区的节点作为种子节点，初始认为该种子节点为社区C。

（2）计算社区C所有邻接点的适应度，将适应度最大的节点加入到社区C中，形成新社区C′。

（3）计算新社区C′中所有节点的适应度，如果存在适应度小于0的节点，从社区C′中删除该节点，并重复该步骤直到不存在适应度小于0的节点。

（4）从（2）开始重新计算，直到社区的邻接点的适应度都小于0，则结束此次扩展，获得一个社区。

LFM算法具有较低的时间复杂度。但是随机选择种子节点造成算法结果的不稳定；同时在计算适应度时仅考虑了节点的局部特征，没有考虑节点的全局影响力，造成社区划分结果准确性较低。

2.2 K-核分解算法

Stephen等人提出的K-核分解算法被广泛应用于网络中核心节点的识别。K-核分解算法通过递归的方式将节点从较低的等级修剪到较高的等级。

算法过程如下：

（1）移除所有度数为1的节点，如果产生度数为1或者小于1的节点就继续移除，直到不存在度数小于等于1的节点为止，这些所有被移除的节点被标记为ki=1。

（2）移除所有度数为2的节点，在此过程中会产生新的度数为2或者度数小于2的节点，这些节点也被移除，在这一步被移除的所有节点被标记为ki=2。

（3）依次类推，直到移除所有节点为止。

通过K-核分解算法可以为每个节点标记ki，ki代表节点的核心程度，其中ki越大表示节点的核心程度越高。

K-核分解算法能够有效地得到节点核心程度，因此ki越大的节点越可能是种子节点。但由于在复杂网络中存在许多相同核心程度的节点，无法判断这些节点核心程度的差异，因此直接引用k-核分解算法会造成种子节点选择的不确定性，从而导致社区划分结果不够稳定。

3 基于K-核迭代因子的重叠社区发现算法

通过分析局部扩展类算法和K-核分解算法所存在的问题，本文引入K-核迭代因子和归一化的节点密度函数，设计了一种新的节点影响力函数，并在此基础上设计了一种社区隶属度函数，提出了基于K-核迭代因子和社区隶属度的重叠社区发现算法KIMDOC。该算法的具体步骤为：

（1）计算所有节点的K-核迭代因子和节点密度，对节点密度进行归一化处理，将K-核迭代因子与节点密度相结合，计算得到节点影响力。

（2）选择节点影响力最大且未被划入社区的节点作为种子节点，形成初始社区C。

（3）从社区C出发，计算邻接节点对于社区C的社区隶属度，把社区隶属度大于阈值的节点划到社区C中，重复此步，直到该社区C不再扩展为止。

（4）重复（2）、（3）两步，直到所有节点都被划到社区为止，最后处理孤立节点，并把相似度高的社区合并，得到最终划分结果。

其中节点影响力计算和节点隶属度计算为KIMDOC算法的核心，下面将对其进行详细阐述与分析。

3.1 K-核迭代因子

为避免直接引用K-核分解算法选择种子节点的不确定性，本文引入了K-核迭代因子的概念，用以区别节点核心程度的差异，K-核迭代因子的计算公式如式（2）所示：

其中δi表示节点i的K-核迭代因子，ki表示通过K-核分解算法得到节点i的核心程度，mki表示在计算ki时总共经过几次迭代，ni表示在mki次迭代中节点是第几次迭代时被移除。

算法1列出了K-核迭代因子的计算伪代码，其中行2的k用来表示K-核的核心程度，行5的m用来记录每轮K-核分解时最多迭代几次，行10的ni用来记录节点i是第几次迭代被移除，行17、18用来计算节点i的K-核迭代因子并将其并到集合S中。

算法1 KIMDOC的K-核迭代因子算法（Kernel Iterative Algorithm，KIA）

输入：复杂网络G=(V,E)；

输出：所有节点的迭代因子S={ δi|i∈V ； }

1.S←Ø；

2.k←1；

3.do

4.T←Ø；

5.m←0；

6. do

7. For each i∈V do

8. if(di＜=K)then

9. remove(V,i)；

10.ni←m+1；

11.T←T∪{i}；

12. end if

13. end for

14.m←m+1；

15. while（T＞0）

16.for each i∈T do

17.δi=k·1 +〔

18.S←S∪{δi}；

19. end for

20.while（V＞0）

21.return S；

如图1所示，K-核迭代因子计算过程为：当k取值为1时，第一次迭代移除的节点为1、2、3、5、9、11，第二次迭代移除的节点为4，第三次迭代移除的节点为6，之后没有度数小于等于1的节点，此次移除结束，其中节点1、2、3、5、9、11的K-核迭代因子为1×（1+1/3），节点4的K-核迭代因子为1×（1+2/3）；依次类推计算出如表1所示所有节点的K-核迭代因子。

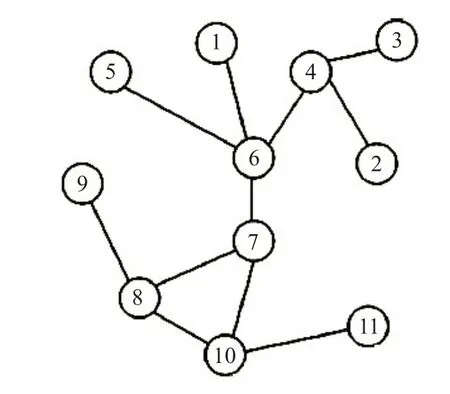
图1 K-核迭代因子示意图

表1 K-核迭代因子算法的过程

3.2 种子节点选择

虽然K-核迭代因子可以进一步区分节点核心程度的差异，但还会产生少数无法区分的节点，例如图1中节点7、8、10，都是在k取值为2时的第一次迭代就被移除了，因此直接通过k-核迭代因子选择种子节点也会造成不确定性。文献[12]的研究结果已经表明，一个节点的度数越大越具有更大的影响力。同时PageRank算法[13]指出节点的影响力由节点的邻接节点的数量和邻接节点的影响力决定。所以，一个节点的影响力由节点和节点周围所有节点决定，本文引入了节点密度的概念。公式如式（3）所示：

其中，Ni表示节点i的邻接节点集，dj表示节点j的度数。

K-核迭代因子作用在点的度数上面，通过公式（2）可以发现，迭代因子不大于节点度数的两倍，而公式（3）所计算的节点密度是度数的累加，会产生一个很大的值，不利于两者的结合计算，因此对节点密度进行归一化处理。首先求出每个节点的密度，找出网络所有节点的最大密度，将每个节点的密度除以最大密度，得到归一化处理的结果，如公式（4）所示：

将K-核迭代因子与节点密度归一化值相结合，将其作为本文的节点影响力。其计算公式如式（5）所示：

通过节点影响力就可以找出种子节点，提高了算法在种子节点选取的稳定性和准确性。

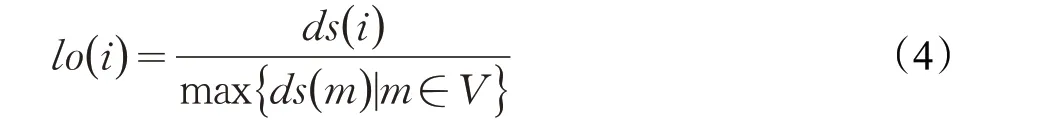
3.3 社区局部扩展

局部扩展类社区发现算法判断一个节点是否加入社区，是通过计算隶属度函数来确定的，所以隶属度函数的正确性对社区划分的结果有很大的影响。本文在节点影响力的基础上设计了一种社区隶属度函数。

在复杂网络中节点越重要，对其他节点的影响力越大。基于这种思想，先定义节点i的邻接节点集的影响力为：

其中N(i)为节点i的邻接节点集，NI(j)为节点j的节点影响力。

因此节点i邻接节点集在社区C的影响力可定义为：

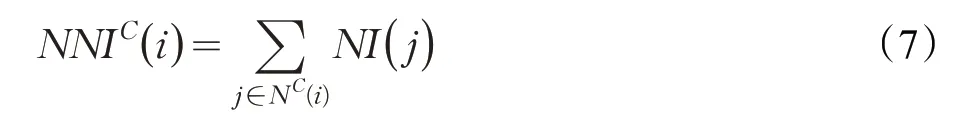
其中NC(i)为节点i邻接节点中属于社区C的节点集合。

社区是联系紧密的节点构成的团或簇。一个节点在社区中的影响力越高，与这个社区联系越紧密，节点越可能属于这个社区。文献[14]通过节点影响力的强弱来判断邻接节点是否加入社区，仅考虑了节点影响力而没有考虑节点加入社区后影响力的变化。因此对节点影响力计算公式进行变形，定义节点在社区C中的影响力。首先根据公式（8）计算社区的K-核迭代因子，把社区C作为一个独立网络图进行计算。

同理，可以得到如下公式：

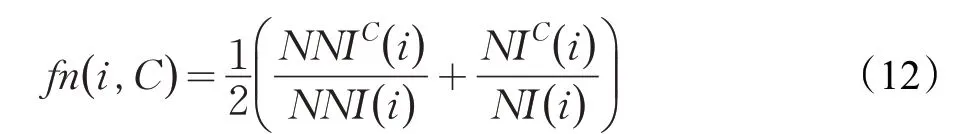
算法2列出了采用社区隶属度函数的局部扩展算法的伪代码，其中行2是得到社区C的所有邻接节点，行4通过算法1得到节点的社区影响力δCi，S为社区C中所有节点社区影响力集合，行6～8是当节点的隶属度大于阈值α时，把节点i划到社区C中。局部扩展就是循环运行算法2，直到社区C不再变化为止。

算法2 KIMDOC的局部扩展算法（Local Extension Algorithm，LEA）

输入：复杂网络G=(V,E)，初始社区C。输出：最终社区C。

1.N←Ø；

2.N←getAdjacentNodes（C）；

3.C′←C∪N；

4.S←KIA(C′)；

5.For each i∈N do

6. if(fn(i,C)＞α)then

7.C←C∪{}i；

8. end if

9.end for

10.return C；

3.4 相似社区合并

划分出来的社区并不是最终社区，可能存在一个节点自己单独成为一个社区，虽然与许多社区相连，但是该节点对每个社区的隶属度都小于阈值α，这种节点被称为孤立节点，对孤立节点的处理方式是：重新计算节点与周围社区的社区隶属度，把该节点划入社区隶属度最高的社区。

社区中可能存在相似度很高的社区，对相似度高的社区可以定义为：存在一个社区中2/3以上的节点同时属于另一个社区，则认为这两个社区相似度高。把相似度高的两个社区合并成一个社区，通过这步处理得到最终的划分结果。

3.5 时间复杂度分析

假设复杂网络G包含n个节点和m条边，Wang等人提出计算K-核迭代因子的时间复杂度为O(n)，计算节点密度要考虑节点的度和邻接节点的度，时间复杂度为O( n×d )，其中d为节点的度，所以寻找种子节点的时间复杂度为O( n+n×d)；从算法2社区局部扩展的时间复杂为O( n×(nC×dmCax))，其中nC为社区C的节点数量，dCmax为社区C中最大节点度，(nC×dCmax)用来计算节点的社区影响力，局部扩展就是重复算法2，因此如果最终结果获得c个社区，则局部扩展的时间复杂度为O( c ×n×(nC×dmCax))；对孤立节点和相似度高社区合并的时间复杂度远远小于K-核迭代因子和局部扩展的计算，因此KIMDOC算法的时间复杂度为O(n+n×d+c×n×(nC×dCmax))=O(c×n×(nC×dCmax))，理想情况下社区数c、社区总节点数nC和最大节点度dCmax远远小于n，因此时间复杂度接近O(n)，在最坏情况下社区数为n并且最大节点度也为n，则找到最终社区的时间复杂度为O(n3)。

4 实验

为了验证基于K-核迭代因子和社区隶属度的重叠社区发现算法（KIMDOC）的有效性，本文算法分别与其他几种具有代表性的发现算法进行比较，待比较的算法分别是COPRA[4]、LFM[8]、QLFM[15]、OMKLP[16]、OCDEDC[7]。实验环境为：内存4 GB，处理器Inter®Core™2 2.00 GHz，操作系统为64位Win7，开发环境为Intellij IDEA2017，开发语言为Java。

4.1 实验数据

本文选取10个真实网络数据集和LFR基准网络[17]进行实验。真实网络相关信息如表2所示。

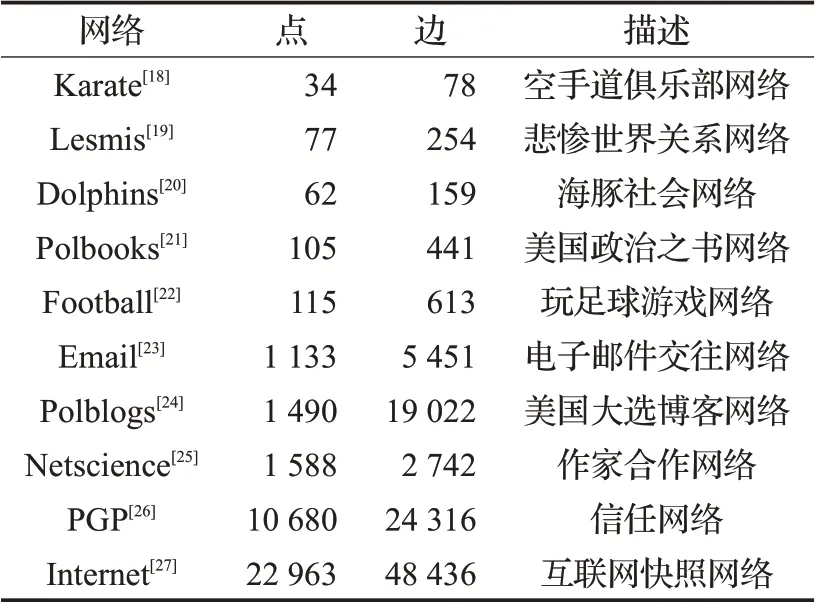
表2 真实网络数据集信息

LFR基准网络是一种人工合成网络，具有真实网络的许多特性，通过调整参数，可以生产不同类型的网络，被广泛应用于复杂网络的研究中。如表3所示，N表示节点数；d表示网络节点平均度数；max d表示网络节点最大度数；min c和max c表示社区的规模；on表示重叠节点的个数；om表示重叠节点所属社区数目；mu表示社区间边与社区内边的比值，比值越大表示社区结构越模糊。

表3 LFR基准网络

4.2 实验评估方法

对于真实网络，本文采用扩展模块度函数EQ[28]来评价，用来判断重叠社区划分的准确性，如公式（13）所示：

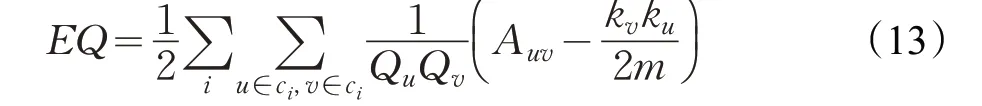
其中，m表示网络中边的数量，Qu表示节点u所属社区的个数，Auv表示u和v之间是否有边，若有边Auv为1，否则为0，ku表示节点u的度。EQ越大表示重叠社区结构越好。

对于人工基准网络，在网络形成时就知道社区划分的结果，社区发现算法的结果可以和真实的划分结果对比，本文采用标准互信息量（NMI）[29]来作为评价指标，NMI越大表示社区发现结果越准确，如公式（14）所示：

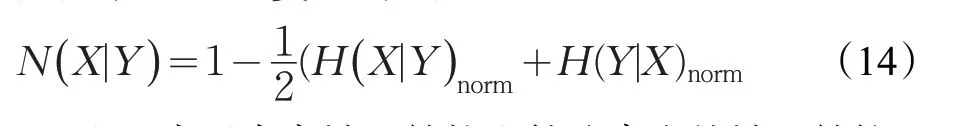
其中，X和Y表示真实社区结构和算法产生的社区结构。

4.3 实验结构与分析

由于COPRA、LFM、QLFM算法都是不稳定算法，所以取10次运行中最好的结果。KIMDOC算法运行多次实验结果是相同的，因此相比LFM算法提升了局部扩展类社区发现算法的稳定性。对于COPRA算法选择v=2；QLFM算法使用原作者论文中的数据0.9；对于OMKLP算法，因为无法得到原始代码，因此直接引用原文中真实数据实验结果，而对人工基准网络不进行比较；对于OCDEDC算法，使用文章中给出的参数ε=0.3，u=4；对于本文算法KIMDOC的阈值α=0.6。

对于真实网路数据集，实验结果如表4所示。从表4可以看出，除了在Polblogs和PGP两个数据集EQ结果较差外，本文算法KIMDOC在真实网络数据集上划分的社区结构扩展模块度比其他算法有所提高，特别是在Football和Internet数据集上提升显著。表明本文提出的算法能够有效地提高重叠社区发现算法的扩展模块度，得到质量更高的社区。

对于人工基准网络的实验结果如图2和图3所示。由于OMKLP算法没有原实验代码，在人工基准网络不进行比较。

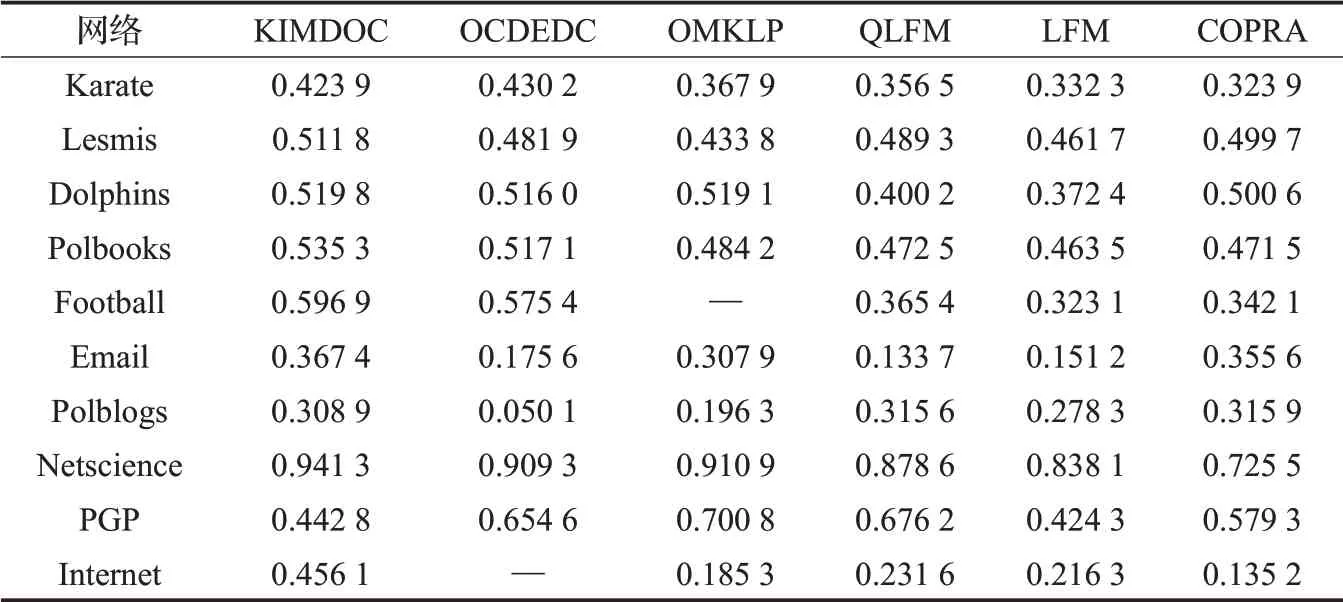
表4 算法在真实数据集上的EQ比较

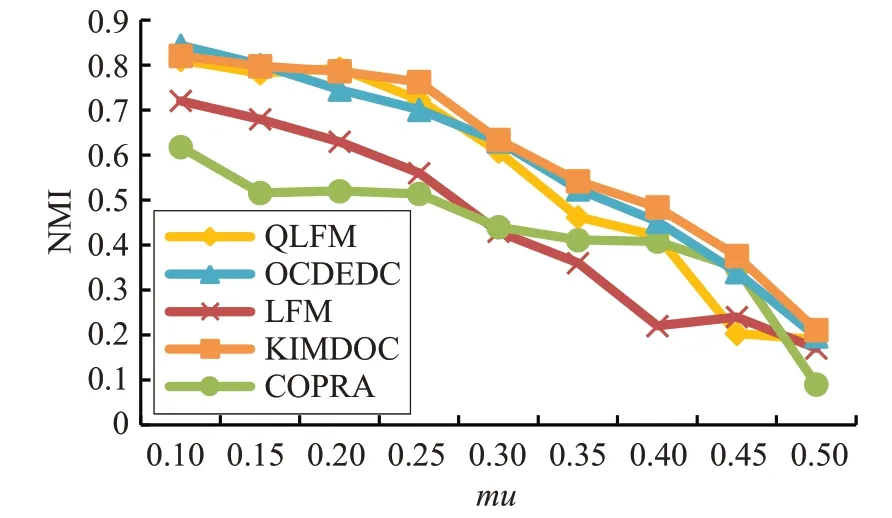
图2 算法在LFR-1000上的NMI比较

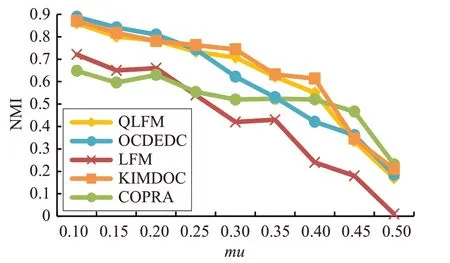
图3 算法在LFR-5000上的NMI比较

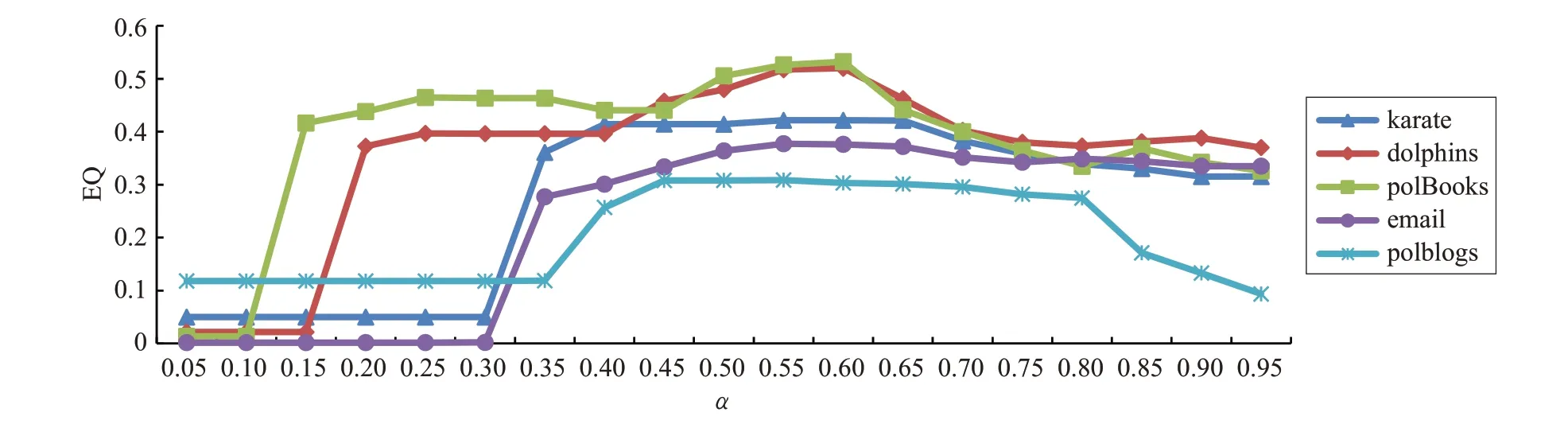
图4 阈值α变化对EQ的影响

从图2和图3中可以看出，KIMDOC算法在两种人工基准网络中，NMI值比其他算法有所提高，且mu在0.25～0.45时有更明显的提高，结果表明本文所提出的方法能有效提高社区划分结果的准确性。

4.4 算法参数取值

KIMDOC中阈值α的选取会影响最终的实验结果，因此对阈值α的变化进行分析和实验。

阈值α的取值范围就是公式（12）社区隶属度函数的范围。通过对公式（6）和公式（7）的定义分析可知：节点i的邻接节点中属于社区C的节点影响力之和NNIC(i)小于等于节点所有邻接节点的节点影响力之和；通过分析K-核迭代因子和节点密度可知，节点在社区中的影响力NIC()i小于等于节点在整个网络的影响力NI()i。因此，可以得出社区隶属度函数的范围是0～1，即阈值α的范围是0～1。

为了探究阈值α对重叠社区划分结果的影响，本文选择五种不同规模的真实网络进行实验，观察不同阈值α的选取对扩展模块度的影响。实验结果如图4所示，横坐标表示阈值α的选取，最小单位为0.05，纵坐标是扩展模块度EQ，随着α的增大，算法在各个网络上的模块度呈现先上升后下降的趋势。当α取0.5～0.65时，算法在绝大多数网络上都具有较高的扩展模块度值。因此，在本文实验中KIMDOC算法阈值参数α的取值为0.6。

5 结束语

在现实社会网络中，复杂网络是普遍存在的，因此，面向复杂网络的重叠社区发现算法具有重要的研究意义和使用价值。本文提出的基于K-核迭代因子的重叠社区发现算法（KIMDOC），通过引入K-核迭代因子的概念，结合节点密度，量化节点影响力，在计算节点社区隶属度时保留了节点网络影响力和社区影响力两个重要特性，既继承了传统局部扩展类社区发现算法的速度优势，又能提高算法的稳定性和准确性。通过在人工基准网络和真实网络数据集上进行测试，可以看出本文算法运行结果理想，对社区划分结果有一定提升。