宽带取样示波器时基误差补偿的新方法研究

2020-02-19朱江淼王世镖赵科佳乔孟元

计量学报 2020年1期

朱江淼，王世镖，赵科佳，乔孟元

(1.北京工业大学信息学部, 北京 100124； 2.中国计量科学研究院, 北京 100029)

1 引言

随着科技的快速进步，高频、高带宽的通信和雷达信号剧增。当利用宽带取样示波器对信号和仪器进行精准测量时，宽带取样示波器的时基误差对测量结果的影响愈加明显，因此对其时基误差的补偿越来越重要。

宽带取样示波器时基误差主要包括时基漂移、时基失真和时基抖动。国内外学者对时基误差补偿算法进行了深入研究，通常采用时基失真和时基抖动独立处理的方法。时基漂移相对简单，通常基于互相关算法[1]估计和补偿。时基失真的估计和补偿算法主要有过零检测法和正弦拟合法，实现也较为简单，但无法补偿时基失真不连续的影响[2]。对于高速取样示波器，美国国家标准技术研究院(NIST)提出了基于多频率多相位的最小二乘算法[3～5]估计宽带取样示波器时基失真，该方法能够修正时基不连续，一定程度上提高了测量准确度。时基抖动具有不确定性，主要通过传统的PDF反卷积方法[6，7]和EEMD综合法[8]补偿时基抖动对测量信号的影响，但会在一定程度上导致平滑失真。通过分析发现，传统单独处理两种时基误差存在明显缺陷：一是两种抖动误差理论上无法严格区分，人为硬性划分具有较大主观性；二是采样不同方法单独处理会引入额外的偏差。

为统一处理时基失真和时基抖动误差，对多通道间同步测量信号进行了理论分析和大量实验验证，发现将时基失真和时基抖动统一处理是合理且可行的。为此，提出正交距离回归算法统一估计，插值法补偿被测信号时基误差的新方法。实验结果表明，该方法能够有效补偿宽带取样示波器的时基误差。

2 时基误差分析

为统一估计和补偿时基误差，设计了如图1所示的三通道同步测量系统。

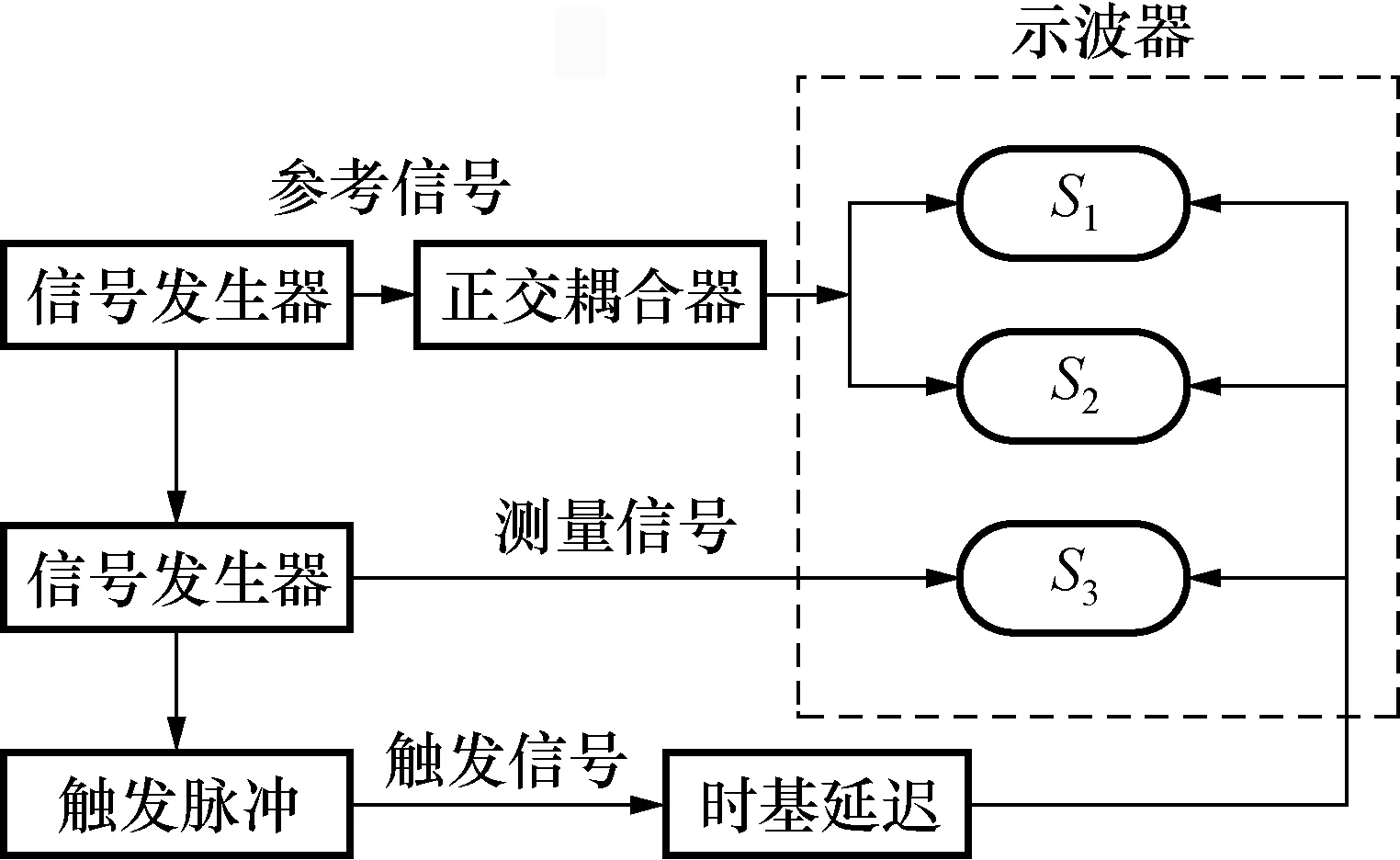
图1 同步测量系统Fig.1 Synchronous measurement system

如图1所示，信号发生器1输出已知频率的正弦参考信号，通过正交耦合器分别接入宽带取样示波器的采样通道S1和S2，信号发生器2输出的被测信号接入宽带取样示波器的采样通道S3。任一采样通道测量信号的时基误差δi可表示为：

δi=di+τsignal+τsampler+τtrigger

(1)

式中：di为时基失真；τsignal为信号源的抖动；τsampler为采样器抖动；τtrigger为时基触发发生器的抖动。

实际实验中，三通道信号均由标准信号发生器产生，其精度较高，信号本身的抖动微乎其微，可忽略其影响，三通道信号源抖动关系如式(2)所示。

τsignal1(i)≈τsignal2(i)≈τsignal3(i)≈0

(2)

对于同一宽带取样示波器相同型号的采样模块而言，不同采样通道造成的抖动基本相同，如式(3)所示。

τsampler1(i)≈τsampler2(i)≈τsampler3(i)

(3)

由于不同采样通道的测量信号共用一个触发，具有相同触发时基，故三通道测量信号的触发抖动[9]引起的误差是相同的，即有：

τtrigger1(i)≈τtrigger2(i)≈τtrigger3(i)

(4)

因此，三通道测量信号的采样时基和采样通道无关，测量信号可统一表示为：

Sp(ti)=Sp(Ti+di+τsampler(i)+τtrigger(i))

(5)

式中：p=1，2，3。

通过以上分析可知，三通道采样信号的时基误差δi是相同的，可用已知频率参考正弦信号S1和S2的信息进行时基误差估计，并用其时基误差估计值对被测信号S3进行时基误差补偿。

3 时基误差估计算法研究

3.1 构建时基误差估计模型

正交距离回归算法[10](ODR)是一种误差模型参数估计方法，主要用于解决因变量和自变量均存在误差的非线性误差问题，具有良好的稳定性和有效性。根据一组近似正交的参考正弦信号[11]的信息，用正交距离回归算法统一估计时基误差，一组近似正交的参考正弦信号模型可表示为：

(6)

式中：yij是第j个参考正弦信号第i个采样时刻的采样幅度值；f是一组近似正交参考正弦信号的频率；h是谐波数，通常取值为3[12]；βik和γrk是第j个参考信号第k次谐波的幅度；Ts是理想的采样间隔；εij表示噪声引起的幅度误差；δi表示第i个采样时刻的时基抖动误差值。

将时基失真和时基抖动总时基误差统一进行分析,可针对式(6)，将诸参数θj=(αj，βj1，…，βjh，γj1，…，γjh)的影响综合为一个函数F，参考信号模型可简化为式(7)。

yij=F(Ti+δi；θj)+εij

(7)

为了能够充分利用两参考信号的信息，得到更加准确的参数估计值，具有权重的正交距离回归算法的误差函数[13]可表示为：

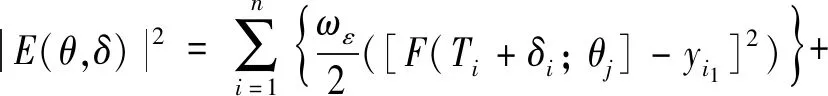
(8)

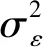
3.2 误差模型参数估计

当误差函数式(8)取得最小值时，获得较为准确的拟合曲线，求得误差模型参数(θ，δ)的估计值，具体步骤如下:

第一，求参数的雅克比矩阵，J(θ，δ)是误差函数E(θ,δ)的雅克比矩阵，矩阵表示为：

(9)

式中：m、n分别表示参数θ和δ的维数。

将雅可比矩阵进行分块可表示为：

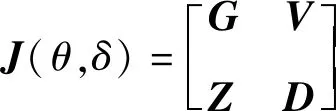
(10)

式中：G是关于参数θ的雅克比矩阵；V是关于参数δ的对角矩阵；Z的所有元素均为零；D是关于δ的常数矩阵。

第二，采用信赖域迭代算法[14]求解迭代步长(h1，h2)。将最小二乘法得到的参数估计值作为迭代初始值，根据文献[11]中给出的迭代步长求解方法，解决如式(8)所示的最优化问题，当目标函数取得最小值时的最小二乘解即为迭代步长。

(11)

式中：H1和H2是(h1,h2)的对角缩放矩阵，用于控制迭代步长的缩放比例；τ是信赖域值。得到迭代步长后，将每次迭代值代入误差函数判断当前迭代误差函数值是否小于上次迭代的误差函数值，若满足，继续迭代，否则停止迭代，则当前迭代值即为参数估计值，最终得到参数(θ，δ)的估计值。此时，可根据参考信号的时基误差估计值δi补偿被测信号的时基误差。

4 实验验证

4.1 实验数据获取

参照图1所示的同步测量方案，准确连接测量仪器设备，用重复频率为10 MHz的晶振对两台 20 GHz 标准信号发生器进行同步。设置参考信号和测量信号均为10 GHz，实际实验中参考信号频率必须已知，被测量信号已知和未知均可,采样点数为4 096个，采样时间窗为0.5 ns。通过宽带取样示波器测量功能得到存在时基误差的被测信号原始波形如图2所示，根据宽带取样示波器自带均方根抖动测量功能，被测信号的均方根抖动高达2.8 ps。

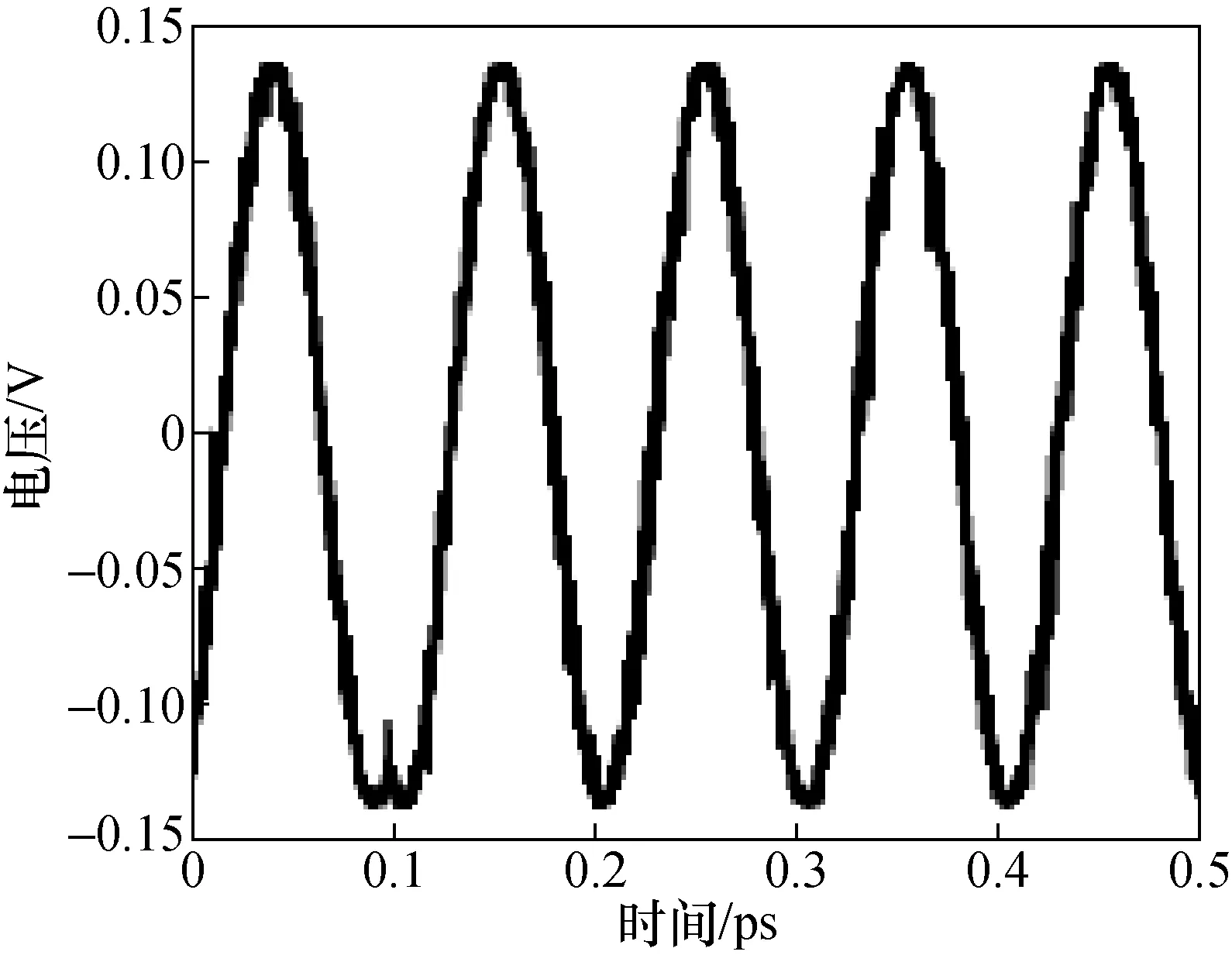
图2 时基补偿前的被测波形Fig.2 Measured waveform before time-base compensation

4.2 时基误差估计

通过正交距离回归算法对同步测量的一组近似正交的参考正弦信号进行时基误差估计，以计算被测信号在每个采样点(共计4 096个)的时基误差值，得到每一点的时基误差估计值如图3所示。

图3 时基误差估计图Fig.3 Time-base error estimation

从图3可看出，被测信号时基误差在0.1 ns处出现突变，这刚好与原始波形不连续处的特征相符合，也进一步验证了该时基误差估计的合理性与准确性。

4.3 时基误差补偿

根据一组近似正交的参考信号，通过正交距离归回算法得到时基误差估计值，通过插值法补偿被测信号的时基误差。首先计算被测信号的真实采样时基，并对新的采样时基序列由小到大进行排序，同时调整对应的采样值，其次取相邻两个采样时刻采样值的均值作为真实采样时刻的采样值，完成对被测波形的时基误差补偿，被测信号时基误差补偿后结果如图4所示。