非贯通裂隙岩体单轴压缩破坏的数值模拟研究

马建华 徐芳超

(1.中国建筑东北设计研究院有限公司 辽宁沈阳 110000; 2.中建东设岩土工程有限公司厦门分公司 福建厦门 361004)

0 引言

在岩石隧道工程、岩石边坡工程中，岩块的强度通常较高，而岩体的强度相对较低，这主要是由于岩体中广泛分布的结构面所造成，岩体中节理等结构面影响着隧道及边坡的设计、施工、运行及长期的整体性与稳定性。

国内外学者针对岩块的试验研究、理论研究报道较多。在试验研究方面：肖桃李，等[1]对人工预制单裂隙类岩材料开展了三轴压缩试验，研究其强度及破坏特性；罗战友，等[2]利用岩石结构面直剪仪对具有不同粗糙度和表面起伏度的类岩材料进行试验研究。在理论研究方面：E.Hoek[3]率先从力学知识入手进行了节理岩体的强度方面探讨，嗣后，其研究成果得到学界公认，结构面强度理论被大量的岩石力学教材所采纳[4-5]。

结构面的存在，使试验研究变得更加困难，也让理论研究中结构面使连续介质力学问题变成复杂的非连续介质力学问题。本文在前辈学者研究的成果基础上，进行非贯通裂隙岩体单轴压缩破坏的数值模拟研究，以阐明在单轴压缩过程岩样内部的力学机制。

1 二维真实破裂过程分析(RFPA2D)软件简介

本次数值模拟研究所使用的软件为二维真实破裂过程分析(RFPA2D)软件，此软件是由唐春安[6-7]教授团队编写开发。该软件采用有限单元法进行应力场的计算分析，并通过给每一个细观单元分配不同的材料参数来考虑固体材料或结构的非均质性。

众所周知，岩石是由各种不同的矿物晶体及微裂隙、微孔隙所组成的一种非均匀性的地质材料。由于这种细观尺度的非均质性和非连续性，岩石材料在空间分布上表现出不同的力学性能。基于此，在RFPA2D软件中假定每一个细观单元的力学性质(如弹性模量、泊松比、单轴抗压强度等)和物理性质(如密度等)服从Weibull分布。其概率密度函数和累积概率函数分别为:

(1)

(2)

式中，α0用来表征岩石材料的力学性能或物理性能的平均值，也称作尺度参数；α为岩石的力学性能或物理性质(如弹性模量、泊松比、单轴抗拉压强度、密度等)；m用来表征岩石材料的非均匀程度，m越小则各个细观单元的物理力学属性越离散，材料越不均匀，如图1所示， 决定了概率密度函数图像的形状，故又将其称作形状参数，在软件中将其称作均质度系数。

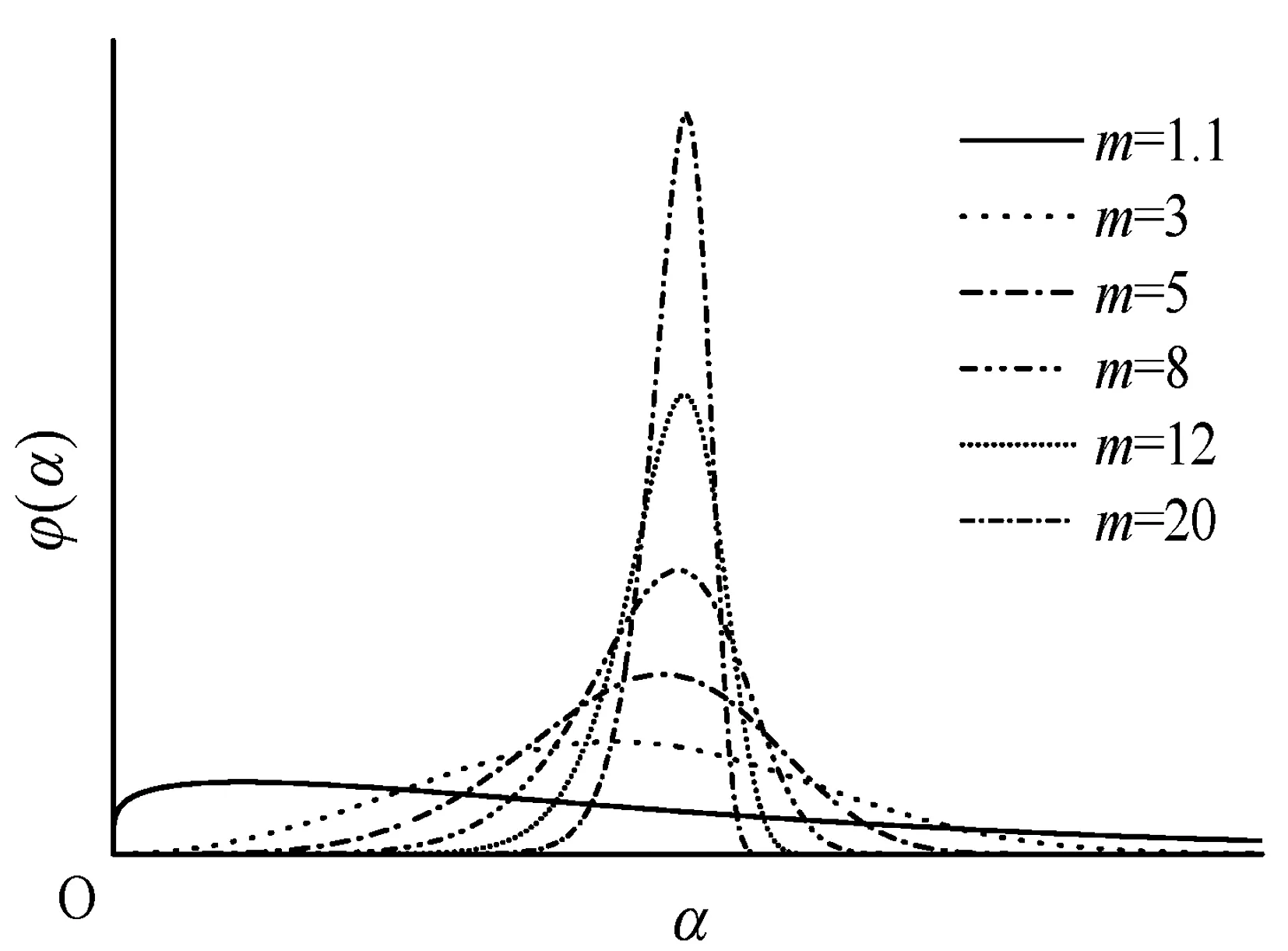
图1 均质度系数m对材料各细观单元物理力学属性分布的影响

另外，RFPA2D软件是基于弹性损伤力学本构关系，采用刚度退化来反映细观单元的损伤情况。一个细观单元在拉伸或剪切荷载作用下，若其应力状态满足最大拉应力准则或Mohr-Coulomb准则时，则达到其损伤阈值，该单元则发生相变，实体单元的刚度则退化为空气单元的刚度，随着荷载的施加退化的单元逐渐增多，从而形成宏观的断裂现象。这种方法有效地实现了采用有限单元法计算材料的断裂现象。

2 数值模型

如图2(a)所示，将预制两条非贯通裂隙的岩样简化为二维轴对称理论模型。由于标准岩样的尺寸为直径50mm，高度100mm的圆柱体，简化后的二维理论模型则为50mm×100mm的长方形。非贯通裂隙的设置是通过在模型高度方向上的中间位置左右两侧分别预制10mm深的裂隙。如图2(b)所示，根据上述理论模型，笔者在RFPA2D软件中建立了相应的二维数值模型，数值模型及非贯通裂隙的尺寸与理论模型一致。单元划分采用等面积四节点正方形单元，总单元个数为200×400。数值模拟过程所需岩石材料参数列于表1中，均质度系数m取为3，数值模型中的所有细观单元的弹性模量均值和取为50GPa，单轴抗压强度均值取为100MPa，各个单元的弹性模量和单轴抗压强度在整个模型基于服从m=3的Weibull分布。数值模拟过程采用位移控制，设置加载速率为1×10-6m每加载步。

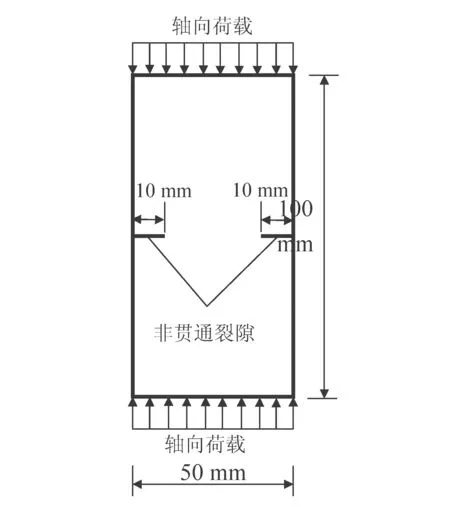
(a)理论模型

(b)RFPA2D数值模型图2 非贯通裂隙岩体双轴压缩数值模型

均质度系数m弹性模量平均值/GPa单轴抗压强度平均值/MPa350100泊松比拉压比内摩擦角/°0.251030

3 模拟结果分析

3.1 应力-应变曲线特征

图3(a)为数值模拟结束后所得出的轴向应力-加载步曲线，将加载步按照所设置的加载速率折算为轴向应变,得到图3(b)中轴向应力-轴向应变曲线。一般的岩石力学中，将全应力-应变曲线分为：压密阶段、弹性阶段、塑性阶段、应变软化阶段[4-5]。从图3(b)中可以看出，除了弹性阶段前的压密阶段外，数值模拟得出的轴向应力-应变曲线与岩石力学中所述单轴加载下的全应力-应变曲线十分相似。值得注意的是，在数值模型中所设置的单元平均单轴抗压强度为100MPa，而数值模拟出的峰值强度为16.6MPa，远小于设置的初始值。这主要是由两方面原因造成：①岩样中部所设置的非贯通裂隙减少了该水平断面的面积；②RFPA2D软件考虑了岩石的非均匀性，各个细观单元的单轴抗压强度按照Weibull分布于均值两侧，这些单元中单轴抗压强度较小的单元率先发生损伤相变，减少了承载压缩荷载的有效面积，致使宏观单轴抗压强度小于细观单轴抗压强度的平均值。

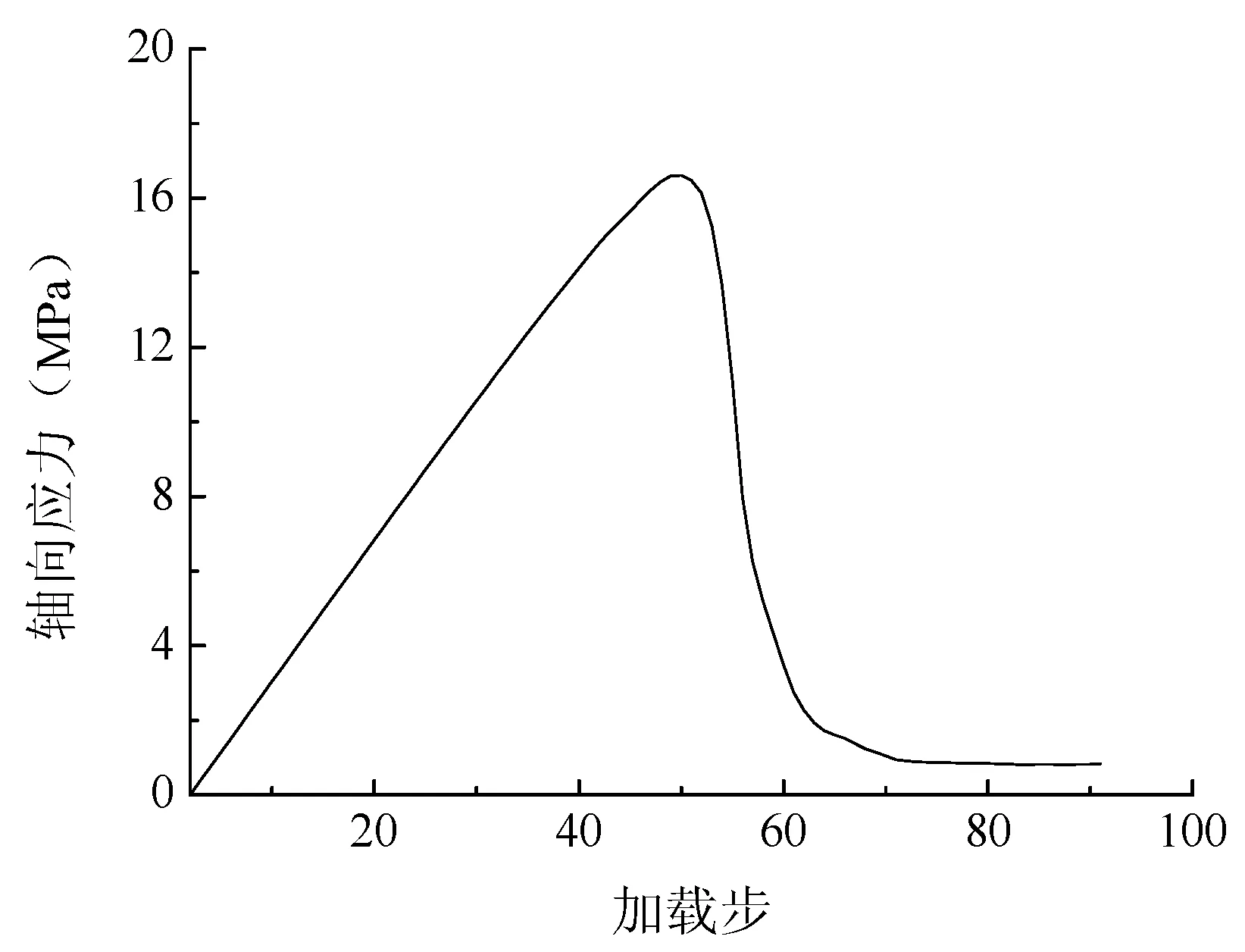
(a)轴向应力-加载步 (b)轴向应力-轴向应变

3.2 破裂过程分析

图4给出预制非贯通裂隙岩样在单轴压缩过程、破坏过程各个细观单元上的最大剪应力分布情况，限于篇幅，仅选取了第1、第20、第40、第50和第60加载步。由图3(a)可知，第1、第20、第40加载步均处于应力峰值前的弹性变形阶段，在图4中，这3个加载步示出的最大剪应力分布云图十分相似：最大剪应力的最大值出现在预制的两条裂隙的尖端，但随着轴向应力的不断增大，最大剪应力的最大值也随之不断增大。

随着轴向应力的继续加载，在第50加载步左右达到应力峰值。这时从图4(d)中圈出的区域可以看出，大量的细观单元发生由实体单元相变为空气单元，隐约形成一条由右侧裂纹尖端附近开始的宏观斜裂纹，待加载至60步，预制非贯通岩样进入应变软化阶段，宏观斜裂纹由右侧预制裂隙延伸至岩样底部，岩石在此时仅有较小的残余强度。

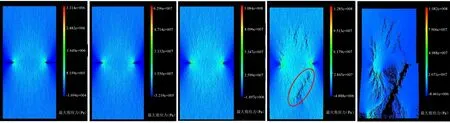
(a)第1加载步 (b)第20加载步 (c)第40加载步 (d)第50加载步 (e)第60加载步

图4 单轴压缩破坏过程中最大剪应力分布

3.3 破坏过程声发射模拟结果分析

在受到荷载作用时，岩石材料内部的矿物晶体间的胶结发生破坏，微裂纹尖端不断扩展，将储存在岩石内的弹性应变能释放出来，这些被释放出的能量可以用敏感度较高的传感器捕捉，所收集的信号被称为声发射信号。唐春安，等[8]从细观损伤力学出发，结合声发射的产生原理，得出了岩石的损伤与声发射具有一致性，即：

N∝D

(3)

其中，N是岩石材料的声发射数；D是损伤力学中的损伤变量，此处表征岩石材料的损伤程度。

RFPA2D软件利用式(3)建立起了岩石材料在受荷过程中各个细观单元的损伤情况与声发射之间的关系。图5给出了的预制非贯通裂隙岩样受到轴向荷载作用下压缩破坏过程累积声发射信号的分布图。图中每一个小圆圈都代表接收到的一个声发射信号，圆圈的圆心表示声发射信号发生的位置，圆圈的直径代表在声发射信号能量在当前加载步的相对大小，红色圆圈表示该加载步之前所有加载步内发生的累积声发射信号，白色圆圈代表当前加载步内所发生的声发射信号。

(a)第1加载步 (b)第13加载步

(c)第20加载步 (d)第40加载步

(e)第50加载步 (f)第60加载步

从图5中可以看出，在加载初期(第1加载步到第12加载步)，岩石所受到的荷载较小，没有声发射信号产生。待加载到第13加载步，岩样内部产生了第一个声发射信号，这意味着岩石内部的一个细观单元的应力状态达到了其损伤阈值。从该声发射发生的位置可以看出，虽然预制裂隙的尖端的最大剪应力值最大，但这次声发射信号并不在裂隙尖端附近，这是由于在RFPA2D中考虑了岩石材料的非均匀性造成。随着轴向荷载的不断增大，可以看出岩样内部的累积声发射信号数量越来越多，发生的位置也越来越有规律，逐渐形成信号集中出现的条带并对应于图4中裂纹不断开展的情况。由此可见，上述模拟有效地反映了预制非贯通裂隙岩样在受到单轴压缩荷载时，内部累积损伤、形核、宏观裂纹出现直至断裂失稳的过程。

4 结论

本研究采用二维真实破裂过程分析软件RFPA2D对预制非贯通裂隙岩样受单轴压缩荷载作用时的破坏过程进行了数值模拟研究，得出的主要结论为：

(1)模拟所得轴向应力-应变曲线与岩石力学中所述单轴加载下的全应力-应变曲线十分相似，但由于RFPA2D软件考虑了岩石材料的非均匀性，所以模拟出的宏观单轴抗压强度小于输入软件中的细观单元平均单轴抗压强度。

(2)在弹性加载阶段，最大剪应力的最大值出现在预制的两条裂隙的尖端，随着轴向应力的不断增大，最大剪应力的最大值也随之不断增大。待加载到峰值附近，宏观裂纹形成。

(3)破坏过程，声发射模拟结果有效地反映了预制非贯通裂隙岩样在受到单轴压缩荷载时，内部累积损伤、形核、宏观裂纹出现直至断裂失稳的过程。